弹道修正火箭弹对面目标射击的最佳CEP研究

宋谢恩,宋卫东,宋高兴

(1.军械工程学院 火炮工程系,石家庄 050003;2.中国人民解放军96265部队,河南 南阳 473139)

火箭炮在作战中主要用于压制或歼灭敌集结有生力量、技术兵种、炮兵等面目标[1]。为提高射击精度,需对现有无控火箭弹进行弹道修正。圆概率误差(circle error probability,CEP)作为射击精度的重要衡量指标,用于表示射击密集度性能,其值等于概率为50%的圆形误差范围的半径,即半数命中圆的半径。在火箭弹弹道修正研究中,只有提前确定了CEP的设计指标,才能对修正能力提出具体要求,进而开展整个修正方案的设计。本文基于射击毁伤理论,考虑实战条件,分析了CEP变化对毁伤效能和效费比等产生的影响,确立了最佳CEP的求解方法。研究表明,最佳CEP与毁伤半径、弹药量、瞄准点数目和分划方式、目标幅员、目标性质等条件都有很强的相关性。本文求解了某些特定条件下的最佳CEP,为火箭弹弹道修正确定了重要设计指标。

1 最佳CEP求解模型

1.1 最佳CEP的提出

在不考虑外界约束的情况下,CEP越小,射击精度越高,射击效果越好,即可以通过集火射击对点目标进行射击,也可以通过分划射击实现面目标覆盖。

在受到效费比、瞄准点数目、目标幅员等的约束时,CEP不再是越小越好。对于弹道修正火箭弹,CEP每减小10 m,成本增加约0.15万元;实战射击中由于生存能力及对抗因素的存在,瞄准点数目不可能无限多;对于较大的目标幅员,CEP过小则无法实现全部有效覆盖。在实际条件约束下,存在最佳CEP,使得毁伤效能、效费比达到最大值。

1.2 毁伤效能计算模型

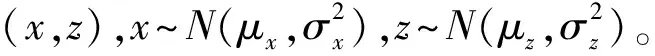
设δCEP为圆概率误差的量符号,其与纵、横向射击精度有近似的关系式[4]:

本文假定纵横向落点相互独立,采用射击落点圆散布模型,纵横向散布的中间误差Ex、Ez相等,则σx=σz=σ,δCEP与落点散布方差σ有如下数值关系:δCEP=1.177 4σ[5]。

将目标幅员划分为等面积网格,以落点为圆心,毁伤半径为半径画圆,被覆盖的网格即为毁伤,计入毁伤面积,并染色。最终统计毁伤面积与总面积之比即为毁伤比,染色结果即为毁伤效果图。

设覆盖次数为i的网格面积为Si,则总面积(即目标幅员):

S=∑Sii=0,1,2,3,…

对于不同目标,达到有效毁伤所需覆盖次数不同。设目标Tω达到有效毁伤所需覆盖次数为ω,则目标Tω的毁伤比为

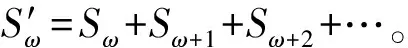
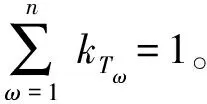
1.3 效费比计算模型

效-费分析是武器系统研制开发过程中的重要环节,其目的在于寻求效能与费用的最优方案[6]。效费比计算公式[7]为

式中:f为武器装备的价值,E为武器装备效能,C为全寿命费用。本文将其简化为

2 最佳CEP求解

2.1 计算初始条件

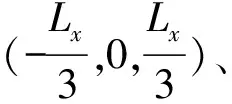
2.2 毁伤效能仿真结果

下面以目标幅员400×400 m2为例给出详细数据图表,并加以说明。图1为经过灰度化处理的毁伤效果图,横轴表示目标正面lz,纵轴表示目标纵深lx,单位均为m,灰度越高表示毁伤覆盖次数越多,未覆盖灰度为0(白色),覆盖4次及以上灰度为100%(黑色)。图1(a)～图1(e)分别为δCEP=0,30,50,100,150 m时的效果图,可以明显看出:随着CEP增大,毁伤覆盖总面积和多次覆盖面积均先变大后变小,CEP变化对毁伤效果的影响清晰可见。

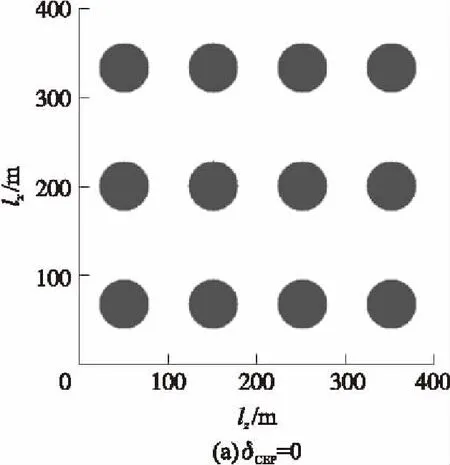
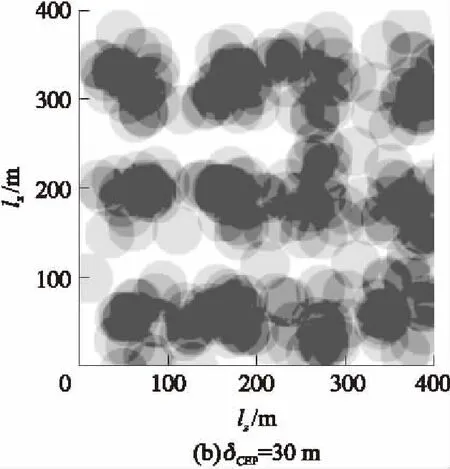
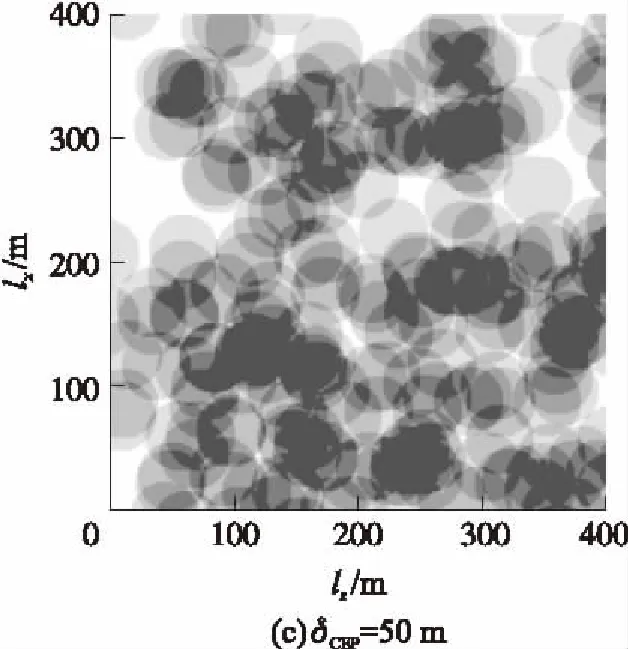
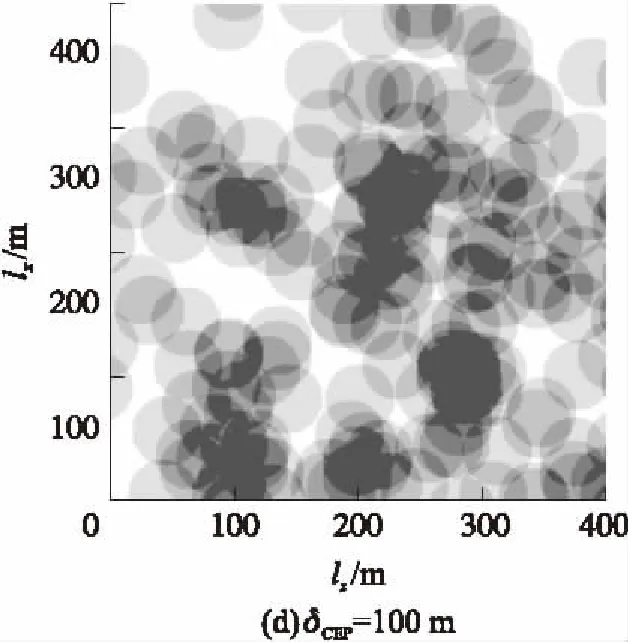
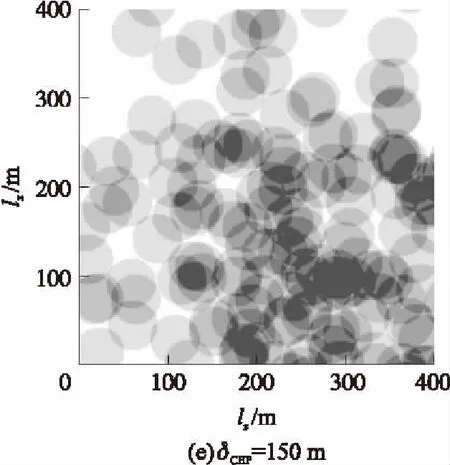
图1 毁伤效果图(400×400 m2)

图2中曲线1、2、3、4、5分别为目标幅员400×400 m2的情况下,人员、轻装甲、重装甲、工事和综合毁伤比曲线,A、B、C、D、E为各曲线的极大值点,其坐标分别为(57,0.88),(50,0.74),(46,0.59),(39,0.46),(47,0.66)。δCEP过大,命中率过低,重复覆盖少,对各类目标毁伤都不大;CEP过小,无法对整个目标幅员有效覆盖,故CEP与毁伤比呈现曲线1和5所示的关系。CEP增大,对于某一个瞄准点来说,重复覆盖减小,而不同瞄准点间的重复覆盖增加,开始前者变化小于后者,体现为覆盖次要求高的目标的毁伤比随着CEP增大而增大,之后后者变化大于前者,体现为相应的毁伤比随着CEP增大而减小。从图可以明显看出这种变化趋势,且这一趋势与曲线2、3、4一致。

图3所示命中率η与CEP呈负相关,CEP由30 m变化到150 m,命中率从98%减小到51%。

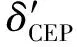
表3中,同一目标幅员,随着δCEP增大,综合毁伤比除200×200 m2一直变小外,其它均先变大后变小,存在极值现象。横向对比,随着目标幅员增大,最大毁伤比变小,对应的最佳δCEP变大,命中率提高。命中率不小于80%,故此修正弹不适合攻击幅员小于200×200 m2的目标。

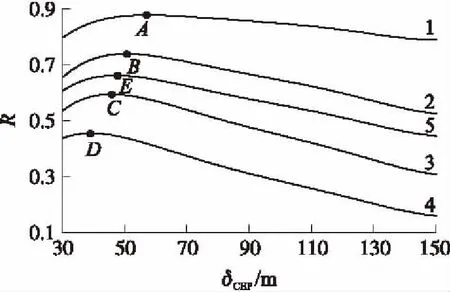
图2 毁伤比随δCEP的变化曲线(400×400 m2)

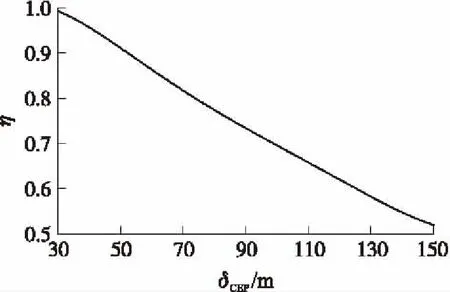
图3 命中率随δCEP的变化曲线(400×400 m2)

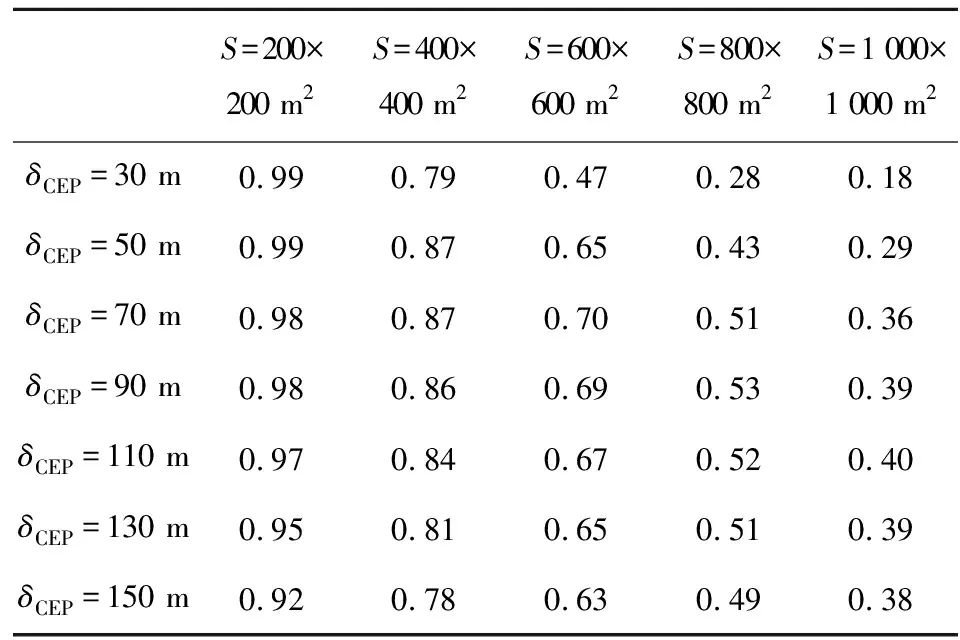
S=200×200 m2S=400×400 m2S=600×600 m2S=800×800 m2S=1 000×1 000 m2δCEP=30 m0.990.790.470.280.18δCEP=50 m0.990.870.650.430.29δCEP=70 m0.980.870.700.510.36δCEP=90 m0.980.860.690.530.39δCEP=110 m0.970.840.670.520.40δCEP=130 m0.950.810.650.510.39δCEP=150 m0.920.780.630.490.38

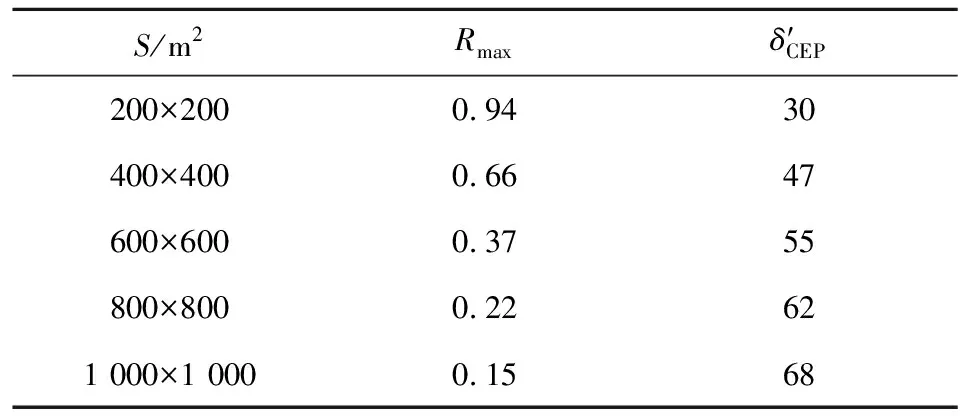
表2 不同目标幅员对应的最大毁伤比Rmax和最佳CEP

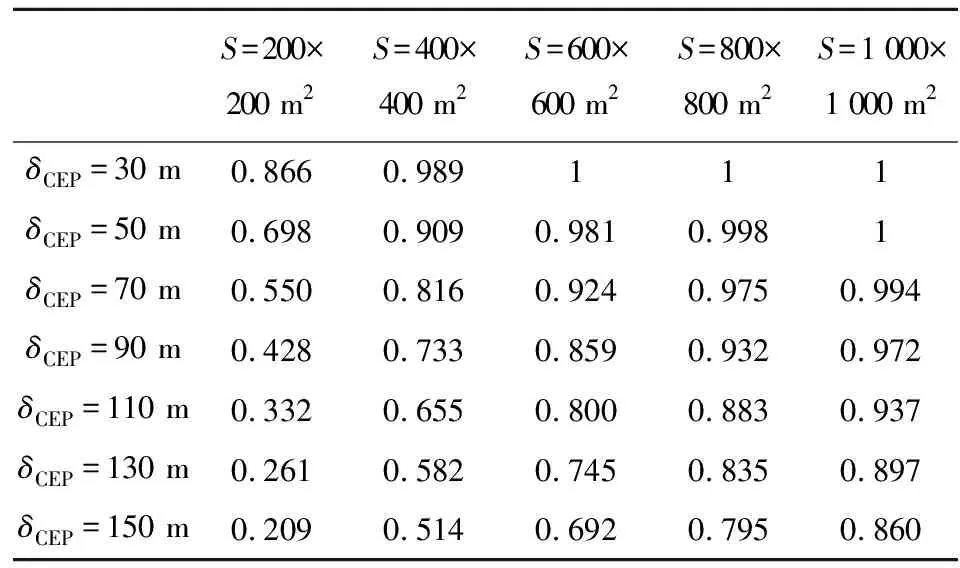
表3 不同目标幅员和不同CEP对应的命中率

2.3 效费比计算

图4为对400×400 m2目标幅员射击时效费比f随δCEP的变化情况,极值点坐标为(54,59),始末点坐标为(30,56),(150,49),效费比先增加5.4%,后降低17.9%。由表4可以看出,随着δCEP的增大,同一目标幅员除1 000×1 000 m2的效费比一直增大外,其它均先变大后变小,存在极值点。表5即为各极值点坐标,随着目标幅员增大,最大效费比对应的最佳CEP先变小后变大。

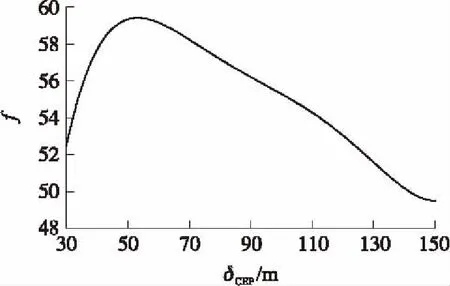
图4 效费比随δCEP的变化曲线(400×400 m2)

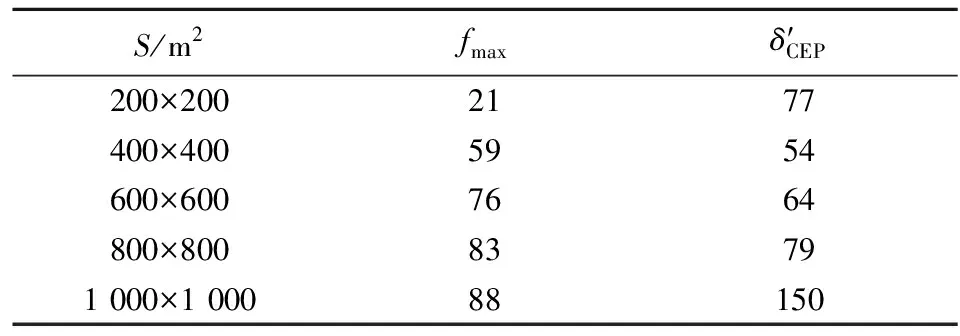
表5 不同目标幅员对应的最大效费比fmax和最佳CEP

效费比是综合毁伤比和成本综合作用的结果,由于δCEP越大成本越低,故成本因素会增大最佳CEP,即效费比对应的最佳CEP要大于综合毁伤比对应的最佳CEP。而200×200 m2综合毁伤比变化幅度较小,对效费比起主导作用的是价格,故最佳CEP较400×400 m2增加幅度大,对应表5中的最佳CEP先变小后增大。

综合前文可得:该型号弹道修正火箭弹适合攻击幅员为500×500 m2左右的目标。幅员过小(200×200 m2),命中率过低,造成大量弹药浪费;幅员过大(1 000×1 000 m2),毁伤比过低。如果通过增加弹药量毁伤比达到毁伤要求,则成本增加过大,甚至超过无控弹[8]。考虑目标幅员、综合毁伤比、命中率3点因素,得出最佳CEP为55 m,即为该型号弹道修正火箭弹的CEP设计指标。

3 结束语

本文基于像素点法通过灰度处理得到毁伤效果图,基于矩阵法求解毁伤效能、效费比,提出针对不同类型的目标的最佳CEP和综合毁伤最佳CEP,最终确定了该型弹道修正火箭弹射击幅员为500×500 m2的目标最能发挥其优势,其最佳CEP为55 m左右。文中对于毁伤比、效费比的计算方法和最佳CEP的确定思路为其它武器系统的效能分析和相关设计指标确定提供了参考。

[1] 程世光,刘晨捷.炮兵兵器与阵地指挥(PHL81式122毫米火箭炮)[M].南京:炮兵学院南京分院,2008.

CHENG Shi-guang,LIU Chen-jie.Artillery weapon and position command[M].Nanjing:Nanjing Artillery College,2008.(in Chinese)

[2] 杨小林,王震宇.矩阵仿真法与战斗部威力评估[J].火力与指挥控制,2010,35(3):86-88.

YANG Xiao-lin,WANG Zhen-yu.Matrix simulation method and warhead power assessment[J].Fir Control & Command Control,2010,35(3):86-88.(in Chinese)

[3] 陈立新.压制火炮作战能力指数研究及应用[D].合肥:合肥炮兵学院,1995.

CHEN Li-xin.Research and application of fighting ability index of suppressing artillery[D].Hefei:Hefei Artillery Academy,1995.(in Chinese)

[4] 姚志军.多管火箭射击精度试验方法研究[D].南京:南京理工大学,2008.

YAO Zhi-jun.Firing accuracy test method of multiple launch rocket system[D].Nanjing:Nanjing University of Science and Technology.2008.(in Chinese)

[5] 张乐,李武周,巨养锋,等.基于圆概率误差的定位精度评定办法[J].指挥控制与仿真,2013,35(1):111-114.

ZHANG Le,LI Wu-zhou,JU Yang-feng,et al.Positioning accuracy evaluation method based on CEP[J].Command Control & Simulation,2013,35(1):111-114.(in Chinese)

[6] 温熙森,匡兴华,陈英武.军事装备学导论[M].长沙:国防科技大学出版社,2002.

WEN Xi-sen,KUANG Xing-hua,CHEN Ying-wu.Military equipment introduction[M].Changsha:National University of Defense Technology Press,2002.(in Chinese)

[7] 王珂晟,邹永显,李永东,等.试论武器装备的效费比分析[J].装甲兵工程学院学报,2003,17(3):55-58.

WANG Ke-sheng,ZOU Yong-xian,LI Yong-dong,et al.Analysis on proportion of effectiveness and life cycle cost of weapon equipment[J].Journal of Armored Force Engineering Institute,2003,17(3):55-58.(in Chinese)

[8] 张永伟,杨锁昌,王新,等.弹道修正弹射击效率分析[J].国外电子测量技术,2012,31(10):49-50,54.

ZHANG Yong-wei,YANG Suo-chang,WANG Xin,et al.Firing efficiency analysis of trajectory correction projectiles[J].Foreign Electronic Measurement Technology,2012,31(10):49-50,54.(in Chinese)