基于内弹道过程的膛内燃烧产物的计算

王 亮,许厚谦,薛 锐

(南京理工大学 能源与动力工程学院,南京 210094)

为进一步提高武器的性能,国内外许多学者对膛口流场进行了深入的研究[1-4]。Jiang Z等[1]数值模拟了含高速运动圆柱形弹丸的膛口流场,获得了较好的流场分布;Sakamoto K等[2]通过引入MUSCL格式计算了在没有弹丸的情况下膛口的流场;曲普、薄玉成、方举鹏等[3]数值模拟了三管并联发射产生的膛口射流,较好地预测了膛口射流与弹丸出膛口后的相互耦合作用;周星、许厚谦等[4]将无网格方法引入膛口流场的数值模拟中,结果较好。但是,膛口流场数值模拟中所需的发射药燃烧产物组分初始数据还无相关文献给出具体的计算方法。郁伟等[5]在模拟含弹丸的膛口流场时引入了内弹道过程,并未加入发射药燃烧产物组分的计算。菅晓霞、刘庆上等[6]提出改进的吉布斯自由能法求燃烧产物平衡组分,仅计算了燃烧产物平衡组分,并没有涉及到其他方面。本文在内弹道计算过程中加入了发射药燃烧产物组分的计算,进一步为膛口流场的计算提供了初始的燃烧产物组分值。发射药的燃烧产物一般是处于高温高压的状态,在本文中视为实际气体,服从范德瓦尔斯状态方程,燃烧产物的计算采用最小自由能法。

1 计算模型

1.1 内弹道模型

建立经典的内弹道模型,提出以下假设:

①点火药瞬间燃完,火药在点火药压力下开始燃烧;②所有的火药燃烧规律遵循几何燃烧定律,且火药的燃烧是在平均压力下进行;③弹丸在膛内运动时,弹丸与膛壁之间不存在空隙,即无漏气现象;④弹丸在膛内平均压力达到挤进压力p0时才开始运动;⑤在整个过程中火药燃烧产物的组分始终保持不变;⑥火药燃气服从范德瓦尔斯气体状态方程。

根据以上假设,可建立经典内弹道数学模型[7]:

(1)

1.2 范德瓦尔斯状态方程

范德瓦尔斯状态方程是范德华在前人研究的基础上提出的第一个比较有意义的真实气体状态方程[8],该方程在理想气体状态方程的基础上分别引进了2个修正项,分别修正由于分子间存在相互作用力和分子占有体积造成的误差,其形式为

(2)

式中:a为反映分子间相互作用力强度的参数;b为反映分子占有体积的常数,其取值见表1;Rg为气体常数;T为气体的温度;ν为气体的比体积。

表1 常见气体的范德瓦尔斯常数[8-9]

2 计算方法

2.1 四阶龙格-库塔方法

本文采用四阶龙格-库塔方法计算求解内弹道方程,具体见文献[7]。

2.2 最小自由能法

本文采用最小自由能方法计算发射药燃烧产物组分值。当温度和压力一定,整个反应体系达到化学平衡时,火药燃烧产物的自由能之和最小;又由于整个系统在整个反应过程中保持质量守恒,可以求出一组燃烧产物的组分值,这就是最小自由能法的基本原理[10]。在本文中,发射药的燃烧产物视为实际气体,服从范德瓦尔斯状态方程。

系统自由能函数:

(3)

式中:G为物质的吉布斯自由能,上标⊖表示标准状态,k为系统中组分个数;ps为系统压力;Ts为系统温度;下标i表示第i种气体,上标g表示气体,ng为气体组分物质的量。

在本文中采用剩余性质[9]的概念计算实际气体的标准自由能:

H=H*+ΔH′,S=S*+ΔS′

(4)

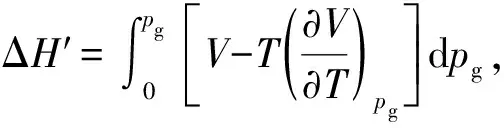
G=H-TS。

式中:H,S分别为真实气体的焓和熵;H*,S*分别为理想气体的焓和熵;pg为气体压力;T为气体温度。

本文在使用最小自由能法计算燃烧产物组分时所采用的温度与压力是通过内弹道方程计算得来的,但是燃烧产物组分的计算并不影响内弹道方程的计算。

3 数值计算结果

本文以59式100 mm高炮为例,采用单一管状药,采用的火药为双芳-3 18/1;火炮构造和装填条件见表2和表3,表中,d为火炮口径,lg为弹丸的全行程长,c为火药长度,φ1为阻力系数。内弹道计算结果如表4所示,表中,pm为最大膛压,tm为达到最大膛压的时间,v0为弹丸出炮口时的速度,tg为弹丸出炮口时的时间,pg0为弹丸出炮口时的膛内平均压力。

表2 火炮构造条件

表3 火炮装填条件

表4 59式100 mm高炮内弹道计算结果

从表4可以观察到,采用本文Fortran程序计算得到的59式100 mm高炮内弹道结果与文献[7]的计算结果以及实验值相比误差均小于1.5%,在误差的允许范围内,所以本文的内弹道程序是满足要求的。

本文采用59式100 mm高炮,对双芳-3 18/1典型火药在内弹道计算的基础上进行了燃烧产物组分的计算。本文中假设燃烧产物为CO,H2O,H2,N2,CO2,因为在实际情况中其他组分只占有很小的一部分,计算结果如表5和图1所示,其中物质的量n是指每千克火药燃烧完全所生成气体的物质的量,以下本文中所提到的“物质的量”均是此含义。

表5 每kg火药在火药燃烧结束时刻和弹丸出炮口时刻的燃烧产物的物质的量

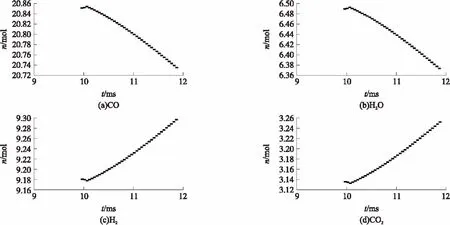
图1 膛内每kg火药从火药燃烧结束时刻到弹丸出炮口时刻对应的燃烧产物的物质的量变化曲线

图1分别给出了膛内每kg火药从火药燃烧结束时刻到弹丸出炮口时刻的主要燃烧产物CO、H2O、H2、CO2物质的量变化曲线。当火药燃烧结束后,n(N)不再改变,n(NO)很小,n(N2)变化不大,其变化曲线不再给出。通过图1可以观察到,从火药燃烧结束时刻到弹丸出炮口时刻膛内燃烧产物组分n(CO)、n(H2O)逐渐变小,n(H2)、n(CO2)逐渐变大,产生这些变化的主要原因是温度和压力的降低使膛内水煤气化学平衡反应移动。但是通过图中数据可以观察到这些变化只是在较小的范围内,这是由于燃气温度相对较低,变化也较小,而且当温度较低时,燃烧产物的组成受压力变化的影响很小[10]。

表5分别给出了在火药燃烧结束时刻和弹丸出炮口时刻燃烧产物的物质的量,以及所对应的压力和温度。通过表5中的数据可以计算得到膛内水煤气反应在火药燃烧结束时刻和弹丸出炮口时刻的平衡常数值Kw,如表6所示。可以观察到本文计算得到的2个时刻水煤气反应平衡常数值与文献[10]的值相差较小,表中,相对误差E是满足要求的。

表6 水煤气反应在火药燃烧结束时刻和弹丸出炮口时刻的平衡常数值

4 结论

本文将内弹道方程与最小自由能法相结合,编写能同时计算内弹道参数和膛内燃烧产物组分的Fortran程序。以59式100 mm高炮为例,验证了本文的内弹道计算结果是能够满足要求的。在内弹道计算的基础上,本文加入了膛内火药的燃烧产物的计算,得到燃烧产物CO,H2O,H2,CO2的物质的量变化曲线。从火药燃烧结束时刻到弹丸出炮口时刻,CO、H2O的物质的量逐渐变小,H2、CO2的物质的量逐渐变大,通过分析发现这是符合实际情况的。另外,通过计算火药燃烧结束时刻和弹丸出炮口时刻的水煤气平衡常数,也可以看出本文的燃气组分计算结果是与实际相符的。所以本文的计算结果是有效的,可以为弹丸出膛口后的流场计算提供初始的数据。但是本文计算结果也有不足之处,在燃烧产物计算中未加入次要组分如NO、O、OH、H等的计算,下一步的工作就是加入这些次要组分的计算,并将其应用于膛口流场的化学反应计算中。

[1] JIANG Z,TAKAYAMA K,SKEWS B W.Wave interactions following the emergence of a supersonic projectile from a tube[C]//17th International Symposium on Ballistics.Midrand,South Africa:IBC,1998:9-16.

[2] SAKAMOTO K,MATSUNNAGA K,FUKUSHIMA J,et al.Numerical anaysis of the propagating blast wave in a firing range[C]//Proceedings of the 19th International Symposium on Ballistic.Interlaken,Switzerland:IBC,2001:289-296.

[3] 周星,许厚谦.无网格算法在膛口流场数值模拟中的应用[J].弹道学报,2011,23(1):23-26.

ZHOU Xing,XU Hou-qian.Application of meshless method in numerical simulation of muzzle flow field[J].Journal of Ballistics,2011,23(1):23-26.(in Chinese)

[4] 曲普,薄玉成,方举鹏.含运动边界的并联发射膛口流场数值模拟预测[J].弹箭与制导学报,2012,32(4):158-160.

QU Pu,BO Yu-cheng,FANG Ju-peng.Numerical simulation on muzzle flow field of multi-barrel gun containing high-speed projectiles[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(4):158-160.(in Chinese)

[5] 郁伟,朱斌,张小兵.耦合内弹道过程的膛口流场数值模拟与分析[J].南京理工大学学报,2009,33(3):336-338.

YU Wei,ZHU Bin,ZHANG Xiao-bing.Numerical simulation and analysis of muzzle flow field coupling with interior ballistic process[J].Journal of Nanjing University of Science and Technology,2009,33(3):336-338.(in Chinese)

[6] 菅晓霞,刘庆上.随机方向法赋初值求火药燃烧产物的平衡组成[J].含能材料,2012,20(2):202-204.

JIAN Xiao-xia,LIU Qing-shang.Calculation of equilibrium composition of combustion products of gunpowder based on random direction method initialization[J].Chinese Journal of Energetic Materials,2012,20(2):202-204.(in Chinese)

[7] 翁春生,王浩.计算内弹道学[M].北京:国防工业出版社,2006:2-15.

WENG Chun-sheng,WANG Hao.Computational interior ballistics[M].Beijing:National Defense Industry Press,2006:2-15.(in Chinese)

[8] 童钧耕,吴孟余,王平阳.高等工程热力学[M].北京:科学出版社,2006:71-106.

TONG Jun-geng,WU Meng-yu,WANG Ping-yang.Advanced engineering thermal dynamics[M].Beijing:Science Press,2006:71-106.(in Chinese)

[9] 田立楠.物性手册查用基础[M].武汉:湖北科学技术出版社,1985:20-25.

TIAN Li-nan.Manual check with the basis of the physical properties[M].Wuhan:Hubei Science and Technology Press,1985:20-25.(in Chinese)

[10] 周起魁,任务正.火药物理化学性能[M].北京:国防工业出版社,1983:38-43.

ZHOU Qi-kui,REN Wu-zheng.Physico-chemical properties of gunpowder[M].Beijing:National Defense Industry Press,1983:38-43.(in Chinese)