基于改进遗传算法的电磁轨道炮电源时序优化
2014-08-28胡玉伟刘志钊王子才
马 萍,胡玉伟,杨 明,刘志钊,王子才
(哈尔滨工业大学 控制与仿真中心,哈尔滨 150001)
电磁轨道炮是一种新概念动能武器,具有初速高、射程远、能量释放易于控制等优点,未来将拥有广泛的应用前景[1-2]。电磁轨道炮的能量来源于电能,通过适当的电路结构,将脉冲电源的电能转化为射弹的动能,使射弹具备较高的出口速度,因此提高电磁轨道炮的性能一直是研究的重点。
文献[3]忽略电磁轨道炮发射过程中的阻力,采用遗传算法求解系统最大发射效率;文献[4]考虑电枢在发射时受到的阻力,运用模式搜索法得到使出口速度达到最大的系统参数;文献[5]和文献[6]将过程集成思想用于系统设计,运用带精英策略的非支配排序遗传算法实现了电磁轨道炮的多目标优化。这些研究的共同特点是基于智能算法直接在设计空间中搜索,利用算法自身的搜索性能获得设计目标的最优解,虽然算法具有全局寻优能力,但是对电磁轨道炮的领域知识利用太少,大大增加了优化时间,降低了寻优效率,若算法参数选择不当,易出现早熟现象,而且优化过程中没有考虑电流波形平稳性要求。
电磁轨道炮发射时,放电电流对系统的性能有重要影响,理想的工作电流波形为梯形[7]。为了获得近似理想的电流,脉冲电源以时序放电方式向系统提供能量。根据这个特点,本文采用多阶段设计策略,将放电过程分成多个阶段,在各个阶段通过对电源时序优化使得电流波形尽量平稳,最终获得近似梯形的电流。遗传算法是一种具有并行计算和全局搜索能力的优化算法,但是存在着收敛速度慢、易早熟等问题,因此,在基本遗传算法中引入精英保留、自适应变异和自适应交叉3种策略,提高算法的全局搜索能力。结合放电电流产生的特点,在优化过程中通过判断新产生电流峰值是否满足电流幅值要求,逐步动态缩小设计变量的搜索空间,进一步提高搜索能力。最后以使用多个电源模块电磁轨道炮为例,时序优化结果表明本文方法不仅改善了求解质量,而且电流波形非常平稳,增强了优化结果的实用性。
1 电源系统拓扑结构及分析
1.1 电源系统拓扑结构
在电磁轨道炮系统中,电源是非常重要的组成部分,其性能直接影响着发射过程和未来的部署。电磁轨道炮对脉冲电源的功率水平、储能密度、可靠性等有很高的要求,目前对脉冲电源的研究主要集中在电容器组、补偿脉冲发电机、电感储能器等[8-9]。在这些储能装置中,电容器组虽然储能密度相对较低,但是技术成熟、充放电功率大、操作简单方便,因此在实验室研究和舰船发射试验中被广泛使用[10-12]。
电磁轨道炮发射时,射弹的速度瞬间从0加速到超高速,对轨道的冲击很大,为了获得平稳的加速过程,轨道内的理想电流波形为梯形。然而单独使用电容器组很难满足电流波形要求,因此实验中通常需要用到多个电源模块。单个脉冲电源模块由储能电容器组、可控硅主开关、调波电感、续流硅堆开关等部件组成,构成脉冲成形网络[13]。各模块通过电缆连接,利用计算机对主开关触发,使电源模块按照一定时序向系统放电。图1是电磁轨道炮采用的脉冲成形网络等效电路图,这种电路结构的特点是放电时序对电流波形调节,使其尽量平稳,续流硅堆导通电流,保护电容器组,防止其被反向充电。图中,C,Rc为储能电容器组的电容值和电阻值;Ld,Rd为调波电感的电感值和电阻值;Rs为可控硅的电阻值;Ro为续流硅堆的电阻值;Lb,Rb为连接电缆的电感值和电阻值;Lr,Rr分别为轨道的等效电感和等效电阻;Ra为金属电枢的等效电阻;Uc为电容器组两端的电压,Uao为轨道两端的电压,in为第n个模块中的电流。

图1 电磁轨道炮脉冲成形网络等效电路
1.2 脉冲成形网络分析
脉冲成形网络通过同步或时序放电方式获得不同幅值和形状的电流波形以满足发射要求。同步放电是时序放电的一种特殊情形,各模块放电开关同时触发,向电磁轨道炮提供高强电流。时序放电是为各模块设置不同的触发时间,按规定时序依次放电,从而获得较宽的脉冲电流。
多模块时序放电过程非常复杂,每个模块的放电状态由主放电开关和续流开关导通状态决定。主放电开关导通状态取决于模块的触发时间,续流开关导通状态由储能电容器组两端电压特性控制。假设开关均为理想开关,即当电容器组两端电压为0时,主放电开关断开,续流硅堆开关导通,各模块的工作状态包括换路前的RLC电路放电状态和换路后的RL电路放电状态。根据模块的不同工作状态建立了第n个模块的数学模型[14]:
(1)
式中:ε(t-tn)为单位阶跃函数,描述了电流调节机制。
电磁轨道炮发射过程中,轨道和电枢使用的是具有一定阻抗的金属材料,轨道两端电压为
式中:i为轨道中的总电流。
随着射弹和电枢向前运动,轨道接入到电路中的长度不断增加,轨道电阻为
发射过程中,电流通过轨道的时间极短,存在趋肤效应,轨道的电阻梯度为[15]
式中:μ0,ρr分别为轨道金属的磁导率和电阻率;hr为轨道的厚度;t为轨道通入电流的时间。
轨道内通入电流会产生焦耳热,轨道和电枢间存在相对运动又产生了摩擦热,这些热量的积累使轨道金属的电阻率发生变化,即[15]
式中:ρr0为轨道金属的初始电阻率,βr是与轨道金属材料相关的常数。
轨道还具有一定的储能作用,相当于可变线圈,轨道的等效电感为
电枢在射弹的加速过程中起着滑动开关的作用,其等效电阻为
式中:μa,ρa分别为电枢金属的磁导率和电阻率;ha为电枢的厚度;d为电枢的长度。
电枢除了起到导通电流的作用外,还将传递电磁力。在发射过程中,电枢和射弹还受到轨道的摩擦力以及弹前空气阻力,在这些力的共同作用下,电枢和射弹沿着轨道向前运动。各种作用力的模型见文献[14]。
2 多阶段设计策略
电磁轨道炮的脉冲电源模块以一定的时序放电,通过汇流开关向系统提供具有很大幅值和脉宽的近似平顶电流,因此实际电流波形的顶部包含有多个幅值相近的波峰。通过分析电源模块的组成和电路结构可知,单个模块放电产生的电流幅值是先增大后减小,只能出现一个电流波峰,因此若要继续产生电流波峰,必然有新的模块接入到系统中。新模块产生的电流与原有模块的电流迭加使总电流增大,从而出现新的电流波峰,平稳电流波形的顶部将包含多个幅值接近的电流峰值。基于这个特点,将电源的放电过程分成多个阶段,在各阶段设计新模块的放电时序,保证新产生电流的最大峰值与已有各阶段的局部电流的峰值接近,从而使电流波形尽量平稳。
2.1 获得期望电流峰值最少电源模块个数的确定
电磁轨道炮发射时轨道内的电流峰值将达到几百kA,受电源模块储能密度和体积的限制,单个电源模块很难提供如此大的电流,因此需要多个电源模块共同放电完成。当电磁轨道炮中使用多个电源模块时,在这些模块同时放电时获得的电流峰值最大,因此,根据期望获得的电流峰值可以确定所需的最少电源模块的个数:
Hm=「Ip,exp/Ips⎤
(8)
式中:「 ⎤为向上取整符号,Ip,exp为期望的总电流峰值,Ips为单个模块内的电流峰值。Hm个电源模块同时放电时得到的电流峰值将超过期望的电流,通过调整各模块放电时序,可以降低电流峰值,从而满足设计要求。
2.2 优化模型
射弹在加速过程中受到的电磁力直接取决于电流幅值的大小,因此电流幅值对射弹的加速性能有重要影响,电源模块应该在允许的电流幅值范围内向电磁轨道炮提供尽可能大的电流。为了保证电流具有一定脉宽,电源模块通过改变放电时序,在多个阶段产生电流峰值,这些电流峰值都将尽可能地接近理想电流峰值,通过对放电过程的控制使电磁轨道炮性能达到最优。因此,对各阶段的脉冲电源时序优化的目标函数为
minE=min(|Ip,exp-Ipl|)
(9)
式中:Ipl为第l阶段电流峰值的最大值。设计电源模块时序的目标是使电源模块放电产生尽可能大的电流,但是电流必须在轨道允许的电流幅值范围内,即满足约束条件:
G=max{Ip1,Ip2,…,Ipl} (10) 采用惩罚函数法处理约束条件,构造的惩罚函数为 F=E+r{max[0,(G-Ip,exp)]}2 (11) 式中:r为惩罚系数。通过将含有约束的优化问题转换为无约束优化问题,再用改进遗传算法对该问题求解,获得脉冲电源模块的最优放电时序。利用多阶段设计策略确定电源模块放电时序的具体步骤: ①使用q1个电源模块向电磁轨道炮放电,利用改进遗传算法优化电源模块放电时序使目标函数(9)达到最小,当优化终止条件满足时,优化过程结束,得到产生第l=1阶段电流的q1个电源模块的放电时序。 ②判断是否还有未使用的电源模块,若存在没有放电的电源模块,则电流阶段数l=l+1,转步骤③;若所有的电源模块都已使用,则转步骤④。 ③使用ql个电源模块继续向电磁轨道炮放电,利用改进遗传算法优化电源模块放电时序使目标函数(9)最小,当优化终止条件满足时优化过程结束,得到产生第l阶段电流的ql个电源模块放电时序,转步骤②。 ④电源模块放电时序优化过程结束,获得电源模块的放电时序,电源模块使用得到的时序向电磁轨道炮放电获得平稳电流。 遗传选择是按照一定概率在父代中选择个体的操作。根据个体适应度值确定选择概率,利用轮盘赌法选择若干个体到下一代。为了保证算法收敛到全局最优解,选择过程中采用精英保留策略。选择时找出当前代中适应度函数值最高的个体,并与进化到目前为止最好个体的适应度值比较,根据比较结果,保留适应度值大的个体到下一代。该方法可以保证优良个体不会被交叉、变异操作破坏,从而提高了群体整体的适应度值,加快了收敛速度。 遗传算法的交叉算子和变异算子是影响算法性能的重要所在,直接关系到算法的收敛性。交叉算子确保了种群中新个体的产生,提高了算法在设计空间的搜索能力。变异算子维持群体的多样性,为选择和交叉过程中丢失的基因进行修复和补充,因此交叉概率和变异概率的确定直接影响算法的收敛速度和精度。鉴于此,采用一种自适应交叉和变异策略,算法的交叉概率和变异概率根据种群进化状况动态调整,以避免种群陷入局部最优,同时可加快收敛速度。自适应交叉概率定义为 自适应变异概率定义为 式中:Pc1,Pc2,Pz1,Pz2为常数;fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;f′为参与交叉的2个体中较大的适应度值;f为变异个体的适应度值。当种群中个体趋于局部最优时,fmax-favg减小,交叉概率和变异概率增大,提高了种群的多样性,确保跳出局部最优。由于采用了精英保留策略,在交叉和变异遗传操作过程中最优个体不会被破坏而保留下来。 对电磁轨道炮的脉冲电源时序优化时,设计变量的取值范围通常是估算给出的,即根据电磁轨道炮发射过程的大致持续时间ts确定时序的变化范围[0,ts]。然而发射过程中多个脉冲电源模块是按照一定的顺序放电,新模块的放电时序依赖于已放电模块的放电状况,每个模块放电时序的取值范围只是整个发射时间的很小部分,因此,在电磁轨道炮脉冲电源时序优化过程中,需要动态缩小时序取值变化区间,提高最优解的搜索速度。 记第j个电源模块的放电时序取值变化范围为[xj,min,xj,max]。由于优化过程使用的是多阶段设计策略,假设在第j个电源模块放电前电流已出现了m个波峰,每个波峰出现的时刻为tm,p,考虑到第j个电源模块将产生新的电流波峰,因此该模块的放电时序将在第m个电流峰值时刻之后,确定第j个电源模块的初始取值范围为 第j个电源模块放电目的是为了在向电磁轨道炮继续提供能量的同时保持电流波形平稳,因此新产生的第m+1个最大电流峰值应该与此前出现的电流峰值尽量一致。然而在进化过程中,由于时序初始变化区间较大,当第j个电源模块的时序td,j取值不合理时,新产生电流可能会继续减小,没有起到稳定电流幅值的作用,如图2所示。表中,i为轨道中的电流,t为轨道通入电流的时间。 图2 电源模块放电时序取值过大产生的电流波形 电磁轨道炮轨道内的电流是新模块放电与已有电源模块放电产生的电流的迭加,若时序继续增大,迭加后的总电流将继续减小,因此为了提高电流幅值,第j个电源模块的放电时序的取值应小于当前值,故将时序的取值范围缩小为 在优化过程中,通过将不能产生新电流波峰的时序更新为取值范围的下限,不断缩小时序取值范围,从而能快速找到最优解。 根据改进的遗传算法原理,利用Matlab语言编制了电磁轨道炮脉冲电源时序优化设计程序,算法流程如图3所示。 图3 改进遗传算法流程图 为了验证本文所提方法在获取最大出口速度和平稳电流波形过程中的有效性,选用13个电容基模块作电源,以金属电枢作推进介质的电磁轨道炮为例,分别使用基于改进遗传算法的多阶段优化方法对电源模块的放电时序设计以及使用遗传算法和粒子群算法对电磁轨道炮脉冲电源的发射时序直接优化设计,并对结果进行比较。各算法的参数选取如下:遗传算法和粒子群算法的种群规模M=50,进化代数Ge=100。基本遗传算法采用的是适应度比例选择算子、中间重组交叉算子和实值变异算子,其中交叉概率Pc=0.8,变异概率Pz=0.1;粒子群算法加速度因子c1=c2=2,粒子飞行速度为最大范围的0.1;本文所提方法将设计变量的优化过程分成多个阶段进行,各阶段的设计变量数量大大减少,精英保留数量为2,采用的适应度比例选择算子和自适应交叉和变异算子,其中交叉概率Pc1=0.8,Pc2=0.5,变异概率Pz1=0.1,Pz2=0.01。由于智能优化存在大量的随机操作,因此每种方法分别独立运行10次,然后统计得到优化结果。 假设发射时允许的最大电流为400 kA,根据式(8)确定达到最大电流峰值的最少电源模块个数为4个,利用改进的遗传算法设计4个电源模块的放电时序从而使产生的电流峰值与期望的最大电流的偏差最小。继续向系统内增加电源模块,利用改进的遗传算法设计电源模块的放电时序使产生的第2个电流峰值与最大电流400 kA的偏差最小,依次类推,获得全部13个电源模块的放电时序。使用13个电源模块按照获得的时序向电磁轨道炮放电,得到射弹的出口速度。表1为3种方法对电磁轨道炮优化得到的结果。表中,vom和voa分别为射弹的最大速度和平均速度,e为优化结果的相对偏差。最大速度是10次优化中射弹出口速度的最大值,平均速度为各次优化所得速度的算术平均值,相对误差为最优值与平均值的偏差占最优值的百分比。方法1和方法2分别为使用遗传算法和粒子群算法直接以出口速度为目标对电源模块放电时序优化的结果,方法3为使用基于改进遗传算法的多阶段优化方法以整个电流波形的波动最小为目标,对电源模块放电时序优化的结果,通过控制发射过程电流波形使出口速度达到最大。 表1 采用不同方法的电磁轨道炮优化结果对比 从表中可以看出,通过本文方法获得的射弹的最大速度为2 179 m/s,高于其他2种方法得到的结果。比较3种方法获得的优化结果的相对误差可以发现,本文提出的方法的相对误差为1.24%,分别小于方法1和方法2的相对误差3.18%和1.87%,因此利用基于改进遗传算法的电源时序多阶段优化方法,通过控制发射过程不仅能得到平稳的电流波形,获得更大的出口速度,而且优化结果的稳定性更好,能够减少重复优化次数。为了进一步分析3种方法的优化结果,绘制了最优结果对应的放电电流曲线,如图4所示。 图4 电磁轨道炮放电电流波形对比 比较图4中的3条放电电流曲线可以看出,脉冲电源模块按照本文方法得到的时序向电磁轨道炮放电,电流曲线波动很小,放电过程非常平稳,多个局部电流峰值均接近于允许的最大电流幅值,而通过对时序直接优化得到的结果进行放电,电流曲线波动较大,局部电流峰值和谷值相差较大,而且部分局部电流峰值小于允许的最大电流幅值。因此,基于改进遗传算法的电源时序多阶段优化方法的性能优于其他2种方法,其原因在于多阶段设计策略通过控制电磁轨道炮发射过程,保证放电电流在允许的幅值内尽可能大,而且使电流接近最大幅值的过程能够保持较长的时间,从而使射弹以较大的加速度状态向前运动,并且这种状态能够持续较长的时间,因此得到了较大的出口速度。电磁轨道炮的电源时序通过多个阶段设计完成,大大缩小了单次优化的设计空间,同时采用精英保留、自适应交叉和变异及动态缩小设计空间策略的改进的遗传算法,进一步提高了寻优的效果。因此,基于改进遗传算法的多阶段优化方法是确定脉冲电源模块放电时序的一种有效方法。 为了保证电磁轨道炮发射过程的平稳性,从电源系统放电过程考虑,提出了一种基于改进遗传算法的电源时序优化方法。 针对电磁轨道炮脉冲电源时序放电的特点,将放电过程分成多个阶段,每个阶段以电流波动最小为目标,利用改进的遗传算法对时序优化,最大限度保持整个放电过程中电流的平稳状态,通过控制放电过程提高电磁轨道炮性能。 在遗传算法的框架中,将精英保留策略引入到选择算子,使优良个体不会在遗传操作中被破坏,提高了算法的收敛速度。同时采用自适应交叉和变异算子,在保持种群多样性的基础上,又保证了算法的收敛性。根据多模块电源放电合成电流的特点,通过动态缩小时序取值空间,提高算法的收敛速度。 通过对多个脉冲电源模块的放电时序优化可以看出,在将放电过程分为多个阶段基础上,基于改进遗传算法的电源时序优化方法的性能稳定,能够提高电磁轨道炮的性能,而且放电过程中电流曲线非常平稳,符合电磁轨道炮发射时期望的电流波形。 [1] WETZ D A,STEFANI F,PARKER J V,et al.Advancements in the development of a plasma-driven electromagnetic launcher[J].IEEE Transactions on Magnetics,2009,45(1):495-500. [2] MCFARLAND J,MCNAB I R.A long-range naval railgun[J].IEEE Transactions on Magnetics,2003,39(1):289-294. [3] 何大娇.电磁轨道炮内弹道优化设计[D].南京:南京理工大学,2008. HE Da-jiao.Optimization design for the inner ballistics of railgun[D].Nanjing:Nanjing University of Science and Technology,2008.(in Chinese) [4] 刘文,张海军,白象忠,等.采用模式搜索法对轨道炮重要参数的优化设计[J].火炮发射与控制学报,2012(3):55-59. LIU Wen,ZHANG Hai-jun,BAI Xiang-zhong,et al.Optimal calculation of railgun launched parameters with internal penalty function method[J].Journal of Gun Launch & Control,2012(3):55-59.(in Chinese) [5] SHI Z J,YU X J.Two-objective optimization design for pulsed power supply[J].IEEE Transactions on Magnetics,2009,45(1):525-530. [6] 范昭楠,于歆杰.基于过程集成的电磁轨道发射系统脉冲电源多目标优化[J].电工技术学报,2010,25(5):20-24. FAN Zhao-nan,YU Xin-jie.Process-integration based multi-objective optimization for pulsed power supply of electromagnetic guns[J].Transactions of China Electrotechnical Society,2010,25(5):20-24.(in Chinese) [7] SATAPATHY S,VANICEK H.Energy partition and scaling issues in a railgun[J].IEEE Transactions on Magnetics,2007,43(1):178-185. [8] 高俊山,黄海,杨嘉祥.小型电磁发射系统初级能源与Pspice仿真[J].电机与控制学报,2007(1):45-49. GAO Jun-shan,HUANG Hai,YANG Jia-xiang.The prime power of the minitype electromagnetic launch system and Pspice simulation[J].Electric Machines and Control,2007(1):45-49.(in Chinese) [9] MCNAB I R.Pulsed power for electric guns[J].IEEE Transactions on Magnetics,1997,33(1):453-460. [10] SCHNEIDER M,WOETZEL M,WENNING W,et al.The ISL rapid fire railgun project rafira part I:technical aspects and design considerations[J].IEEE Transactions on Magnetics,2009,45(1):442-447. [11] VERACKA M J,BOYER C N,NERI J M.Automatic multishot operation of an electromagnetic launcher[J].IEEE Transactions on Plasma Science,2011,39(1):153-156. [12] 林福昌,李劲,姚宗干.电磁发射兵器用电容器的选取[J].兵工学报,2003,24(3):416-418. LIN Fu-chang,LI Jin,YAO Zong-gan.Choice of capacitors used in electromagnetic launcher[J].Acta Armamentarii,2003,24(3):416-418.(in Chinese) [13] 董健年,宁广炯,黄新华.脉冲形成网格(PFN)技术研究[J].弹道学报,1997,9(3):48-52. DONG Jian-nian,NING Guang-jiong,HUANG Xin-hua.The technical study of pulse forming network(PFN)[J].Journal of Ballistics,1997,9(3):48-52.(in Chinese) [14] HU Y W,MA P,YANG M,et al.Validation and optimization of modular railgun model[C]//Proceeding of the 16th International Symposium on Electromagnetic Launch Technology.Beijing:IEEE Computer Society,2012:1-6. [15] BERNARDES J S,STUMBORG M F,JEAN T E.Analysis of a capacitor based pulsed power system for driving long range electromagnetic guns[J].IEEE Transactions on Magnetics,2003,39(1):486-490.3 改进的遗传算法
3.1 精英保留策略
3.2 自适应交叉和变异算子
3.3 动态缩小时序取值区间

3.4 算法流程
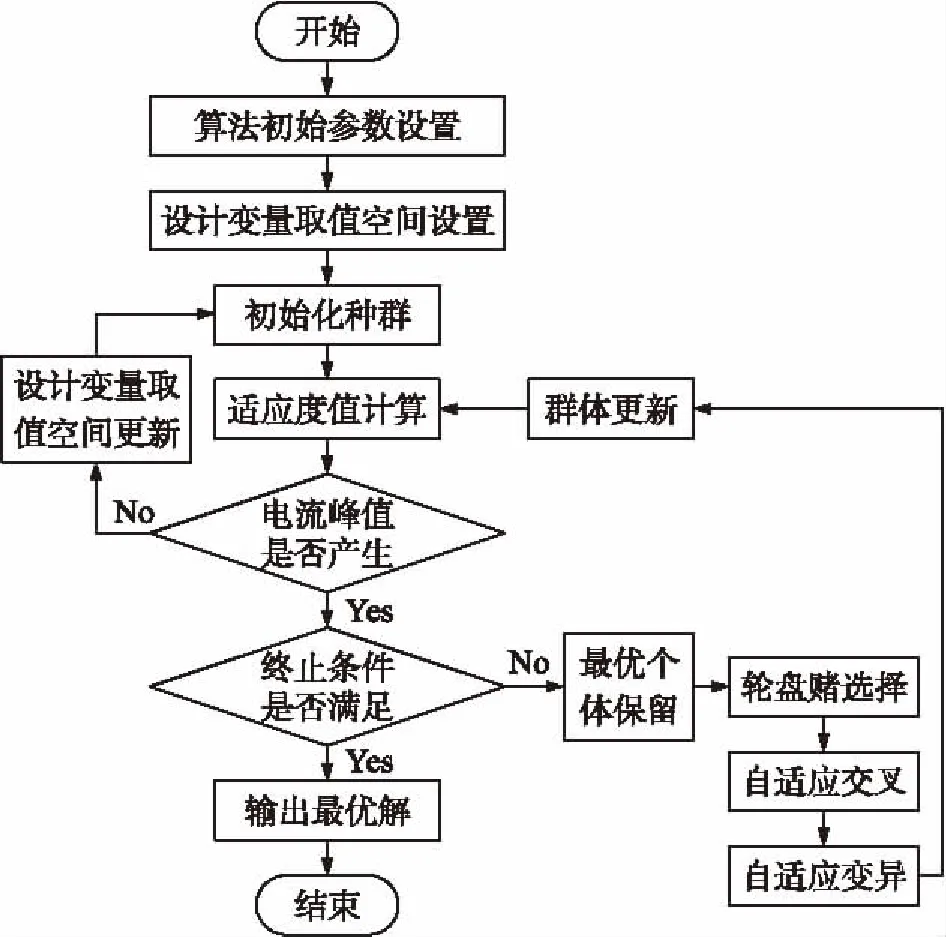
4 实例应用


5 结束语
