基于水动力-结构模型的波浪载荷计算方法

任慧龙，孙葳，李辉，童晓旺

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

近年来，随着船舶与海洋工程业的不断发展，出现了很多新船型和海洋平台形式，这对浮体结构设计方法提出了新的要求，传统的基于规范公式的结构设计方法正逐步被直接结构设计方法所取代。直接结构设计方法能够提高浮体设计的安全性和经济性，但对浮体的外载荷计算及结构分析精度都提出了更高的要求［1-2］。

在浮体结构分析过程中，用于水动力计算的面元数量级为O(103)，而用于结构分析的网格外壳则较为精细，其量级可达O(104)甚至更高［3］。为了顺利进行结构分析，必将涉及到如何将水动力计算中的波浪压力转化到结构模型上这个问题。通常是将水动力网格上的波浪压力通过插值、映射等方法传递到结构单元上，张海彬［4］采用线性插值方法得到结构网格节点的水动压力，但水动力网格和结构网格之间的差异会引起所表达的几何信息不同，压力转化将不可避免地带来误差，这种情况下很难得到一个平衡的外载荷力系。此外，忽略水动力计算中考虑的附加载荷对结构模型的影响使得寻求一个完全平衡的外载荷力系更加困难，而结构模型的平衡性是保证有限元准静态分析获得正确结果的关键［5］。

本文针对上述问题进行了研究，结合法国BV船级社提出的水动力模型与结构模型相结合的水动力计算方法［6］，构造了一种与结构分析协调的三维频域波浪载荷直接计算模型。通过建立水动力模型和结构模型之间的联系，计算结构网格控制点的速度势，进而实现结构网格上波浪压力的直接计算。在此基础上，对各种载荷成分的加载方式及合理性进行了讨论分析。

1 基于水动力-结构模型的载荷计算

1.1 结构网格控制点处速度势计算

假定流体理想不可压缩，流动无旋，基于三维线性频域势流理论，流体的速度势可分解为如下形式:

式中:φI、φD、φR分别表示入射势、绕射势和辐射势，ω为波浪频率。

根据速度势满足的物面条件，在水动力模型上建立分布源密度σ所满足的边界积分方程［7］:

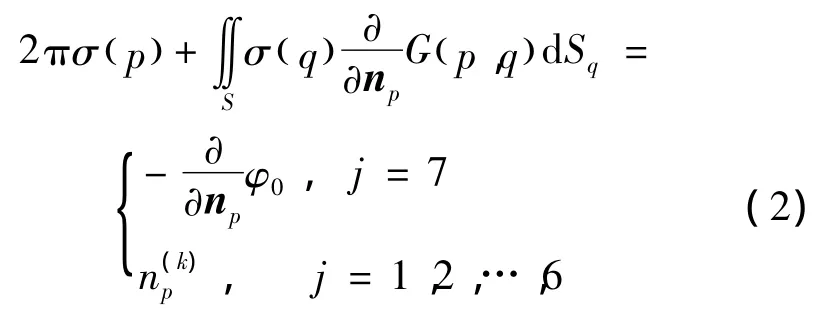
式中:p和q分别为场点、源点，φ0为单位波幅入射势，S表示浮体湿表面，np表示面元法向量，指向浮体内部。

引入三维无航速无限水深或有限水深格林函数G(p，q)［8-9］，应用边界元法对式(2)进行数值离散，将其转化成线性方程组进行求解:

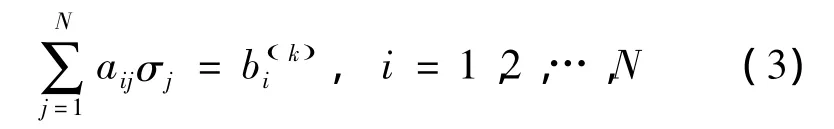
式中:N为水动力模型划分的网格个数，其中:

应用基于分布源模型的边界元法解决满足定解条件的速度势边界值问题时，速度势的表达式在流域内是连续的。因此，结构网格控制点处的速度势可以表示成物面上的分布源形式:

式中:φ(PS)为结构网格控制点处的速度势;PS和QH分别表示结构网格和水动力网格上的点(如图1所示)。

图1 水动力－结构模型Fig.1 Hydro-structure model

1.2 流体载荷计算

结构模型的流体静力载荷计算与水动力模型相似，只需在结构模型上进行积分即可。则流体静力系数:

式中:k，l=1，2，...，6 ，{η}为浮体六自由度运动;Fg为重力分量;pHlS为浮体各模态运动引起的静水压力变化部分，其中:

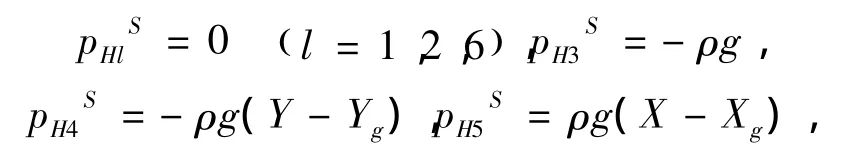
(Xg，Yg，Zg)为浮体重心位置，ρ为海水密度，g为重力加速度。

根据线性化的伯努利方程，扣除静水压力变化部分的浮体湿表面水动力压力可表示为

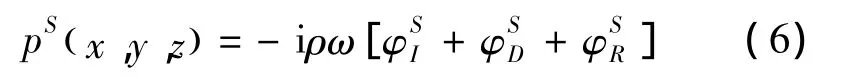
流体动力载荷可由上述水动压力沿结构模型湿表面积分得到，则波浪激励力和辐射力分别为

1.3 运动方程求解与波浪压力直接计算

浮体在规则波中的运动方程为

式中:［M］为刚体的质量矩阵。

由于按线性势流理论计算的横摇兴波阻尼较粘性横摇阻尼而言，只是很小的一部分，为了合理地预报浮体横向运动，需对横摇阻尼系数进行粘性修正。

求解上述运动方程，得到浮体六自由度运动响应，进而直接计算结构网格控制点处的波浪压力:

1.4 加载到结构模型上的各项载荷分量

最终施加到结构模型上的外载荷由以下4个部分组成:

1)波浪压力。通过式(10)在结构网格控制点处直接计算得到包含静水压力、入射压力、绕射压力及辐射压力在内的总波浪压力，加载到平均湿表面的每个结构网格上。

2)惯性力-ω2mij。值得注意的是，对于散货船和载液型船舶而言，散货和液货对舱壁有内压，因此需将货压以压力的形式加载到舱壁上，而此时货物的惯性力则需单独加载，不在全船惯性力范围内。

3)重力分量Fg。由于结构分析与运动方程(式(9))均在与浮体固结的动坐标系下求解，因此结构模型加载时需考虑由于坐标系转动而产生的重力分量

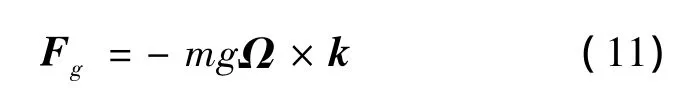
式中:Ω=(η4，η5，η6)分别对应横摇、纵摇和艏摇。

4)粘性横摇阻尼力。由于在水动力计算中考虑了粘性横摇阻尼的影响，因此结构模型加载时也应计入。假设粘性横摇阻尼仅由船侧舭龙骨引起，则考虑将其以节点力的形式加载到结构模型的舭龙骨范围内。每个节点的粘性横摇阻尼力与该点舭龙骨和流体之间的相对速度成比例，即

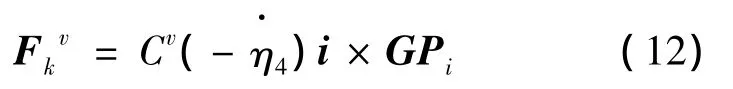
式中:GPi=(YPi-Yg)j+(ZPi-Zg)k;为节点位置。

粘性系数Cv可通过各节点的粘性横摇阻尼力对重心取矩求和得到:

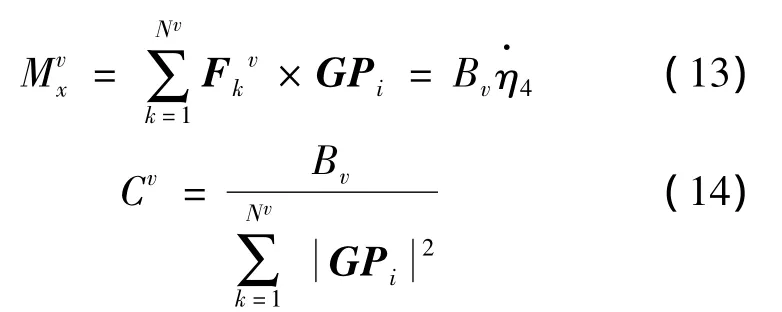
式中:为粘性横摇阻尼力矩，Nv为舭龙骨范围内的节点个数，Bv为粘性横摇阻尼系数。

2 载荷计算程序系统

基于水动力-结构模型的波浪载荷计算程序系统如图2所示，包括以下3个功能模块:

1)结构有限元网格的提取和处理模块(GETMESH)。模块功能:将通用结构分析软件 MSC.NASTRAN输出的结构模型转化为水动力计算的格式。

2)水动力计算模块(HYDSC)。模块功能:根据输入的水动力、结构网格信息，求解水动力网格中心点的分布源密度并计算三维无航速频域GREEN函数，最终得到结构网格控制点的速度势。

3)运动与载荷计算模块(WASTR)。模块功能:计算结构模型上的水动力系数及波浪激励力，求解浮体六自由度运动方程，得到直接用于结构模型加载的各载荷分量。

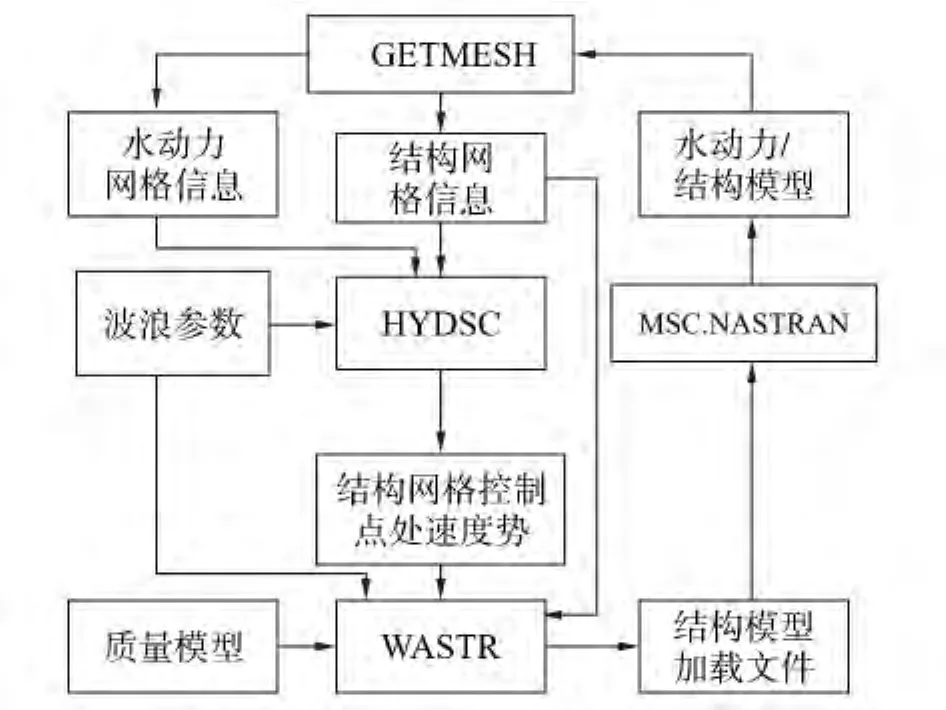
图2 水动力－结构模型载荷计算程序系统Fig.2 Calculation system of wave loads based on hydro-structure model

3 实船数值计算与分析

应用上述计算程序对补给船在规则波中的运动及载荷响应进行预报，并与基于水动力模型的波浪载荷计算结果进行比较。该补给船的基本计算参数见表1，应用有限元软件MSC.PATRAN建立的水动力及结构模型见图3(水动力网格2 190个，结构网格17 922个)。

表1 补给船的基本计算参数Table 1 General parameters of replenishment ship

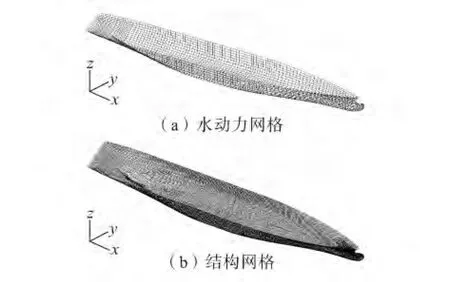
图3 水动力网格和结构网格Fig.3 Hydrodynamic and structural meshes

3.1 水动力计算结果比较

从水动力系数、运动及剖面载荷对比结果(图4～8)可以看出，2种波浪载荷计算模型得到的水动力计算结果吻合良好，剖面载荷之间的差异是由于波浪压力在不同模型(水动力网格和结构网格)上积分引起的，说明基于水动力-结构模型的波浪载荷计算方法是可行的，实现了波浪压力在结构控制点的直接计算。图中和L2)分别表示无因次垂荡附加质量和横摇阻尼系数，，∇为排水体积;η3a和η4a分别表示垂荡和横摇运动幅值;My和Fy表示垂向波浪弯矩和水平剪力，β为浪向角，S.T.表示站号。

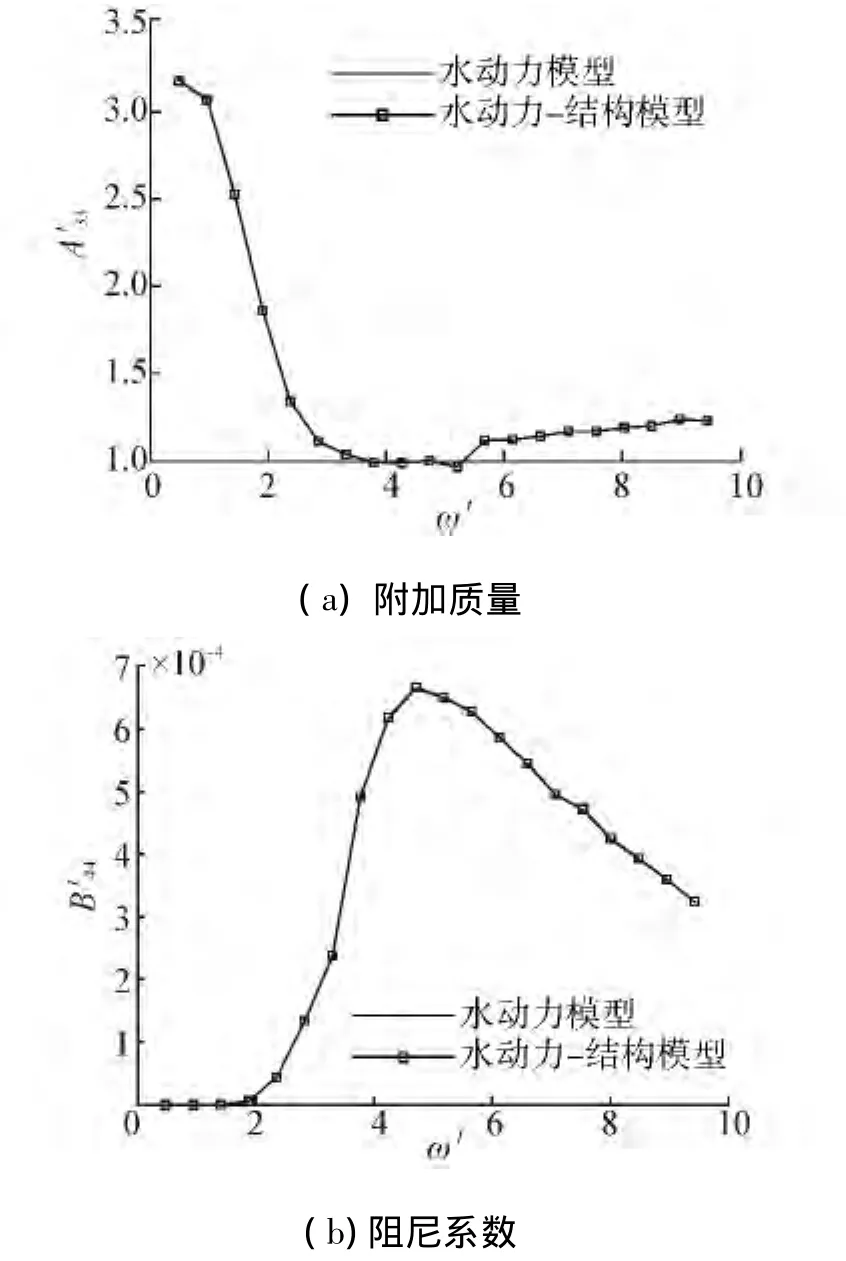
图4 无因次水动力系数Fig.4 Non-dimensional hydrodynamic coefficients

图5 垂荡幅频响应(β=0°)Fig.5 Heave amplitude-frequency responses(β =0°)

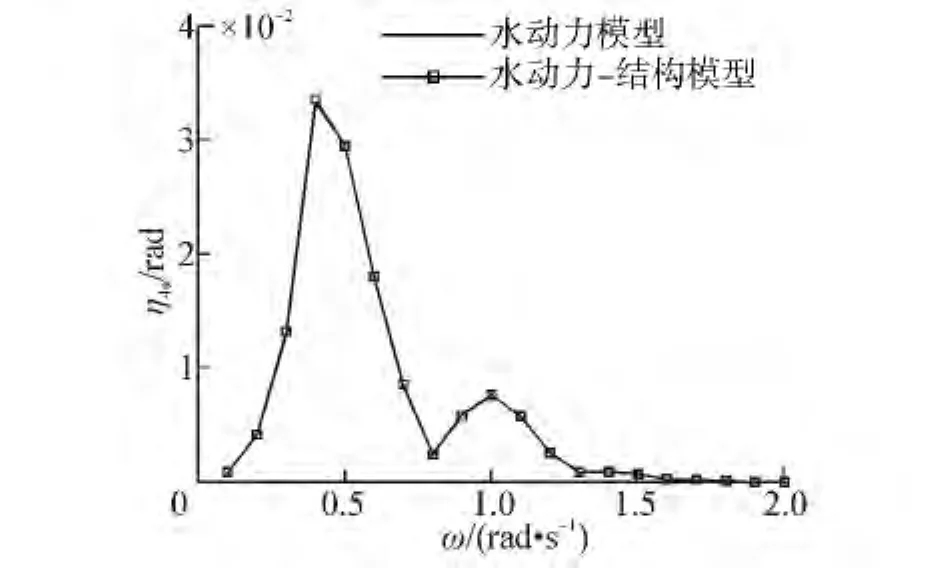
图6 横摇运动幅频响应(β=60°)Fig.6 Roll amplitude-frequency responses(β =60°)

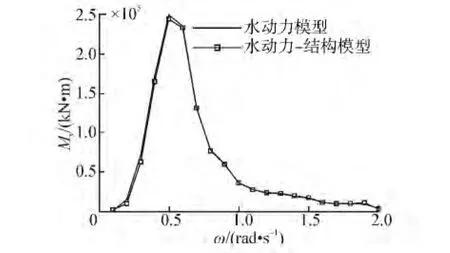
图7 船中剖面垂向波浪弯矩幅频响应(β=0°)Fig.7 Vertical bending moment amplitude-frequency responses of middle section(β =0°)

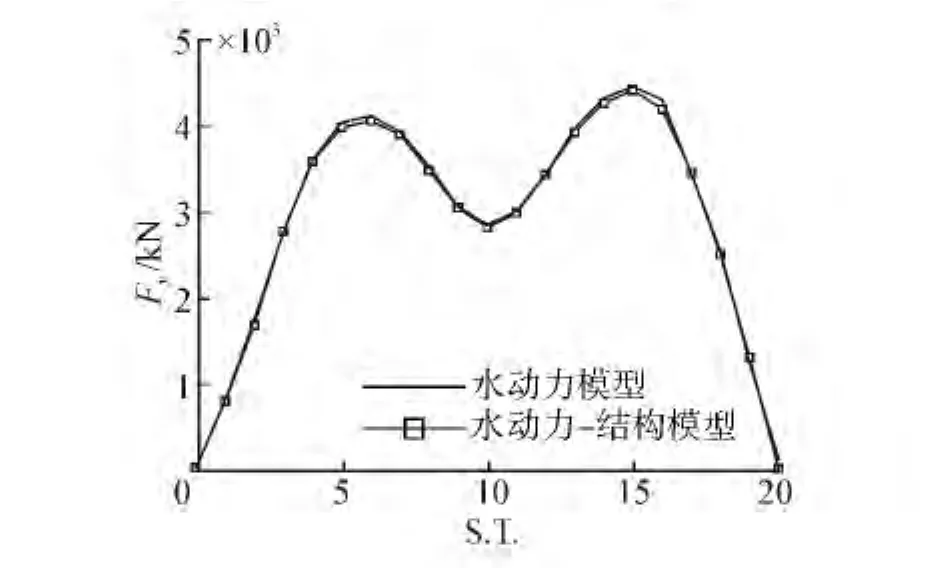
图8 沿船长分布的水平剪力幅值响应(β=60°，ω=0.8)Fig.8 Horizontal shear force amplitude responses along length direction(β =60°，ω =0.8)

3.2 结构模型平衡性分析

表2为迎浪和横浪状态下加载到结构模型上的各项载荷分量及平衡性对比结果。可见:1)2种载荷计算方法得到的波浪诱导惯性载荷及由于坐标系转动引起的重力分量差异很小;2)波浪压力相差较大。补给船的艉部型线变化较为剧烈，这是导致压力转化产生误差造成结构模型不平衡的主要因素;3)在横浪状态下，为了保证水动力计算模型与结构分析模型所受的载荷一致，粘性横摇阻尼力在结构模型加载时不可忽略。

表2 加载到结构模型上的外载荷(ω=0.5)Table 2 External loads loading on structural model(ω =0.5)

4 结论

本文给出的基于水动力-结构模型的波浪载荷计算方法，为直接结构设计提供了一种有效的技术手段。通过研究，可以得出以下结论:

1)2种模型的水动力计算结果吻合良好，验证了所采用方法的有效性。

2)结构分析中的模型加载情况应与水动力计算中的模型受力情况一致。其中，需考虑2种模型的坐标变化产生的重力分量、结构和内部载体的惯性力以及水体粘性力等。

3)本文方法可以保证加载到结构模型上的各项载荷分量在任何工况下都能达到惯性平衡，为浮体结构分析提供可靠的依据。

［1］赵耕贤.船舶与海洋结构物设计中的关键技术之一(结构强度)［J］.船舶，2000，25(6):22-35.ZHAO Gengxian.Structure strength-one of the key design technologies for ship and offshore structures［J］.Ship ＆ Boat，2000，25(6):22-35.

［2］崔维成，祁恩荣，黄小平.船舶结构强度预报/评估方法的现状和未来发展趋势［C］//船舶结构力学学术会议论文集.舟山，2005:159-170.CUI Weicheng，QI Enrong，HUANG Xiaoping.The present situation and future development trend of the ship structure strength prediction and assessment method.［C］//Proceedings of Ship Structural Mechanics Conference.Zhoushan，2005:159-170.

［3］张健.浮式结构与柔性构件的耦合分析方法研究［D］.哈尔滨:哈尔滨工程大学，2012:8-32.ZHANG Jian.Investigation on coupling analysis between floating structures and flexible structural members［D］.Harbin:Harbin Engineering University，2012:8-32.

［4］张海彬.FPSO储油轮与半潜式平台波浪载荷三维计算方法研究［D］.哈尔滨:哈尔滨工程大学，2004:138-149.ZHANG Haibin.3-D Computational method of wave loads on FPSO tankers and semi-submersible platforms［D］.Harbin:Harbin Engineering University，2004:138-149.

［5］朱胜昌，陈庆强，江南.整船准静态分析的有限元模型自动加载及载荷修正技术［J］.船舶力学，1999，3(5):47-54.ZHU Shengchang，CHEN Qingqiang，JIANG Nan.Techniques of auto-loading and amending external node forces for whole hull model in FEM strength calculation［J］.Journal of Ship Mechanics，1999，3(5):47-54.

［6］MALENICA S，STUMPE E，DELAFOSSE V，et al.Some aspects of hydro-structure interfacing in seakeeping［C］//Proceedings of International Offshore and Polar Engineering Conference.San Francisco，2006:312-317.

［7］戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京:国防工业出版社，2008:20-35.

［8］王如森.三维自由面Green函数及其导数(频域无限水深)的数值逼近［J］.水动力学研究与进展，1992，7(3):277-286.WANG Rusen.The numerical approach of three dimensional freesurface Green function and its derivatives(frequency domain-infinite depth)［J］.Journal of Hydrodynamics，1992，7(3):277-286.

［9］刘日明，任慧龙，李辉.有限水深格林函数及其导数的改进Gauss-Laguerre算法［J］.船舶力学，2008，12(2):188-196.LIU Riming，REN Huilong，LI Hui.An improved Gauss-Laguerre method for finite water depth Green function and its derivatives［J］.Journal of Ship Mechanics，2008，12(2):188-196.