DFT和FT-IR相结合研究糠醛与溶剂的相互作用
2014-08-25陈慧
,, ,陈慧
(1.浙江工业大学 药学院,浙江 杭州 310014;2.浙江工业大学 绿色化学合成技术国家重点实验室培育基地,浙江 杭州 310014)
溶剂效应是指同一物质在不同极性的溶剂中,其物理化学性质发生改变的一种效应,其本质是在溶液中,溶质和溶质之间存在着范德华力、静电作用、氢键作用和空间位阻等[1].这些作用力大小与溶质和溶剂分子的性质和结构密切相关.绝大多数化学过程是在溶液中进行的,还有许多生物体的生化过程也是在溶液中进行的,溶剂为这些反应提供了“反应场所”,不同的溶剂影响着化学反应的反应机理、反应速率以及反应的平衡常数[2-4],因此,溶剂效应研究一直是国内外化学工作者所关注的课题[5-6].
糠醛,又称2-乙酰呋喃,已被广泛用作重要的化工原料[7].糠醛是由戊聚糖在酸的作用下水解生成戊糖,再由戊糖脱水环化而成.在生产过程中,萃取溶剂种类对糠醛收率有着较为明显的影响.因此,研究糠醛的溶剂效应具有一定的理论意义.目前,研究溶剂效应常用方法有:光谱分析法和理论计算,特别是理论计算已引起化学工作者的兴趣[8-13].笔者采用密度泛函理论(DFT)和傅立叶红外光谱(FT-IR)相结合方法研究糠醛在各种溶剂中O,O-cis和O,O-trans的构象转化,考察了羰基伸缩振动频率与溶剂参数的相关性,探究糠醛与溶剂相互作用机制,为糠醛的生产提供一些理论依据.
1 实验部分
1.1 仪器和试剂
Nicolet 5700傅里叶变换红外光谱仪,配有Ge/KBr分光器和DTGS检波器(美国热电尼高力仪器公司),Gaussian 03软件包(美国Gaussian公司).糠醛购于上海金山亭新化学试剂厂.实验中所用的有机溶剂均为分析纯,使用前按文献[14]进行纯化处理.
1.2 FT-IR测定方法
以纯溶剂作为背景,在液层厚度0.1 mm的KCl固定液体池中测定各种溶液中糠醛的红外光谱,扫描次数为40次,光谱的分辨率为1 cm-1.糠醛浓度为6.0×10-3mol/L.
1.3 理论计算方法
糠醛在溶液中存在着两种旋转异构体,即羰基氧与呋喃环上的氧在同侧的顺式糠醛(O,O-cis)和在异侧的反式糠醛(O,O-trans)[15-16].这两种异构体结构由Chem 3D Ultra 8.0(美国Cambridge软件公司)给出,然后用DFT理论在B3LYP/6-311++G(d)基组水平上进行最低能量优化两种异构体在各种溶液中结构,直至Hessian矩阵分析无虚频.相应的溶剂环境采用了导体极化连续模型(CPCM).为了证明优化得到的结构是全局势能面最低,在DFT/B3lyp/6-311++G(d)水平上进行简谐振动频率计算.所有的理论计算均在Gaussian 03软件上完成.
顺反式糠醛的结构式分别为
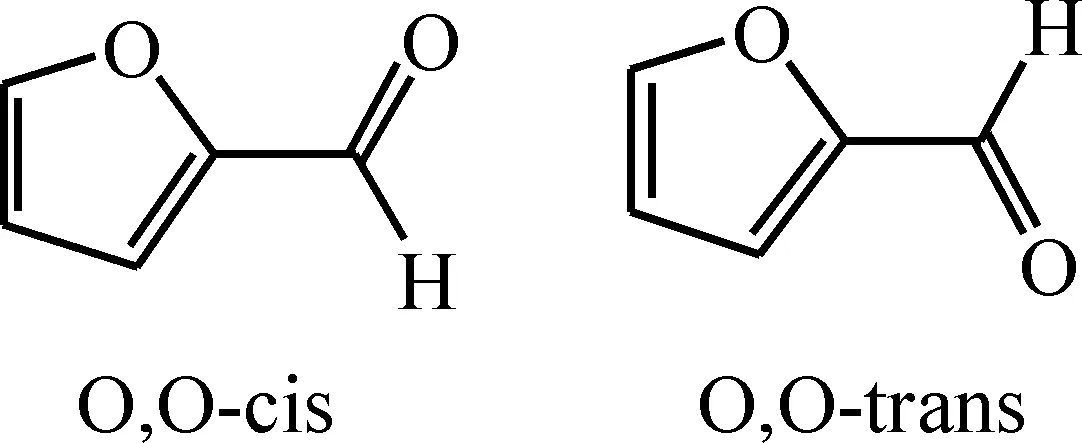
2 结果与讨论
2.1 构象优化
在DFT/B3LYP/6-311++G(d,p)基组水平上,糠醛在各种溶剂中的O,O-cis和O,O-trans构象进行优化,其结果如表1所示.分子总能量越低,分子结构越稳定.从表中可见,随着溶剂极性的增加,O,O-cis和O,O-trans糠醛的总能量都逐渐减小,表明了O,O-cis和O,O-trans糠醛结构随溶剂极性增大趋于稳定.在气态和非极性溶剂中,O,O-cis糠醛的总能量大于O,O-trans糠醛;在极性溶剂中,O,O-trans糠醛的总能量大于O,O-cis糠醛.这表明了O,O-trans糠醛在非极性溶剂中相对较稳定,而O,O-cis糠醛在极性溶剂中较为稳定.从表1还可发现:O,O-cis糠醛的偶极矩大于O,O-trans糠醛,分子间偶极-偶极作用使O,O-cis糠醛在极性溶剂中相对更稳定.

表1 糠醛异构体的总能量和偶极矩以及溶剂参数1)
从图1可知:O,O-cis和O,O-trans糠醛的总能量及偶极矩与溶剂介质的介电常数的倒数间具有良好的线性关系,其线性回归方程分别为
Ecis=-(343.462 8±0.000 1)+
(0.017 8±0.000 3)/εr2=0.997 5
(1)
Etrans=-(343.451 5±0.000 1)+
(0.014 6±0.000 2)/εr2=0.997 4
(2)
μcis=(6.592±0.016)-(2.474±0.049)/ε
r2=0.995 8
(3)
μtrans=(5.511±0.013)-(2.007±0.039)/ε
r2=0.995 8
(4)
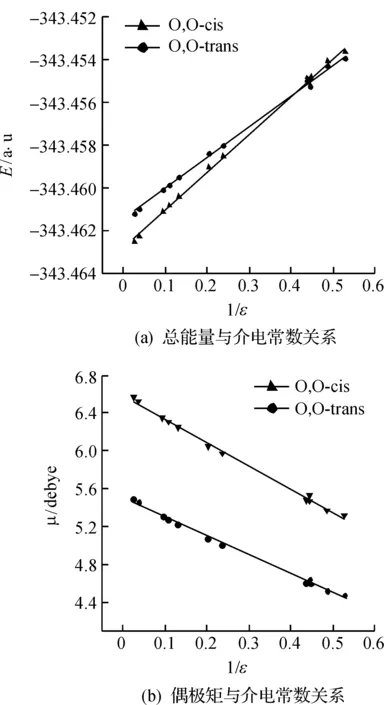
图1 糠醛的总能量和偶极矩与溶剂的介电常数的关系
随溶剂极性增大,O,O-cis和O,O-trans糠醛的总能量随之下降,而且O,O-cis糠醛下降幅度明显大于O,O-trans糠醛,这进一步表明了O,O-cis糠醛在极性溶剂比O,O-trans更为稳定,糠醛旋转异构体的稳定性与溶剂的极性大小密切相关.
根据麦克斯韦-玻尔兹曼分布方程,可以计算出糠醛的两种旋转异构体的分子数目比,即
(5)
式中:Ntrans和Ncis分别为O,O-trans和O,O-cis糠醛的分子数目;ΔE为O,O-trans和O,O-cis的能量差;R为理想气体常数;T为绝对温度,K.其计算结果列于表1.结果表明:在非极性溶剂或气相中,O,O-trans糠醛的数目大于O,O-cis,而在极性溶剂中,O,O-cis糠醛的数目大于O,O-trans.这说明了随着溶剂极性增大,O,O-trans构型向O,O-cis构型转变.
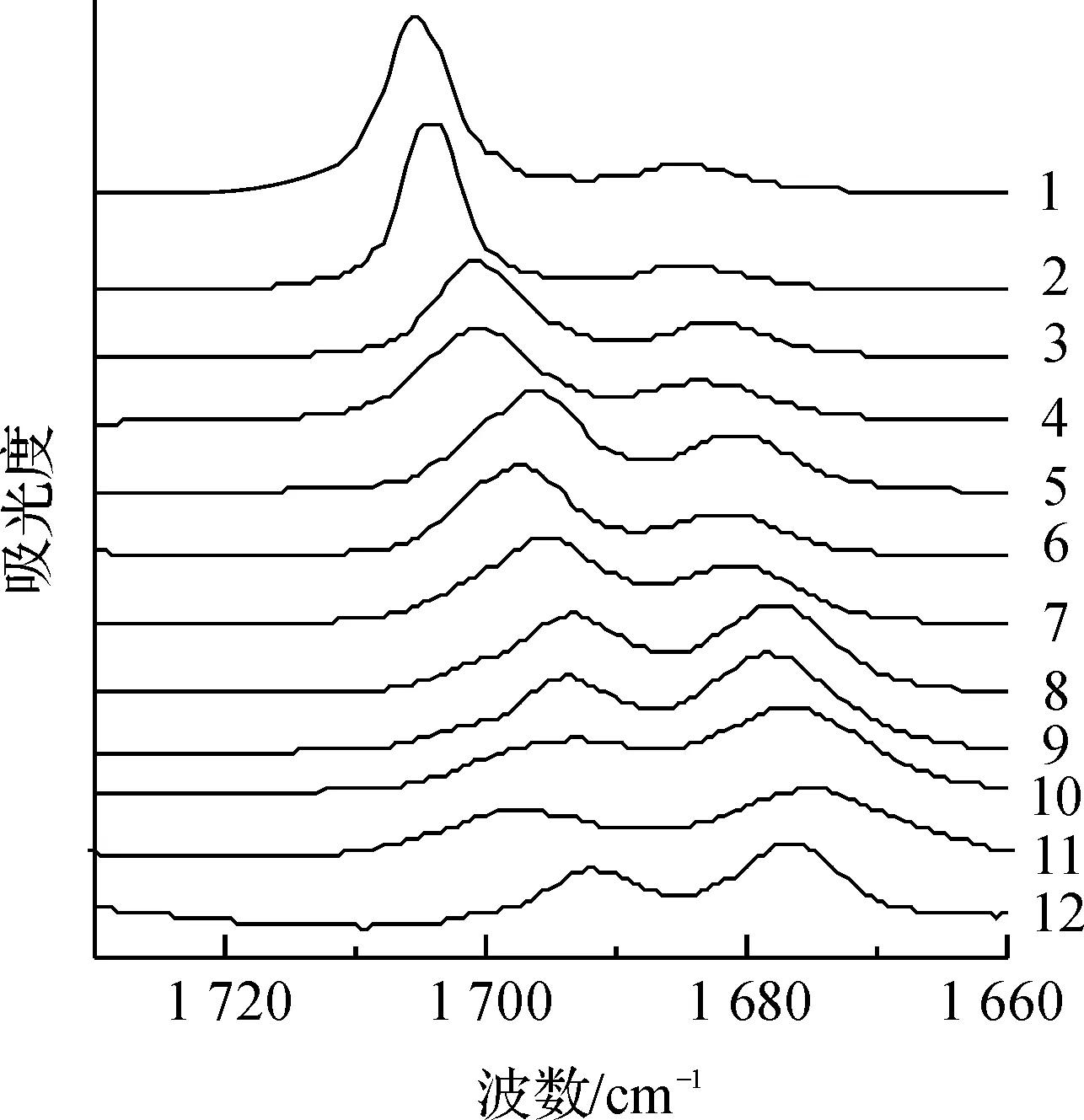
1-正已烷;2-环已烷;3-四氯化碳;4-乙醚;5-苯;6-甲苯;7-四氢呋喃;8-1,2-二氯乙烷;9-二氯甲烷;10-氯仿;11-乙醇;12-乙腈
2.2 糠醛的红外光谱
在12种溶剂中糠醛羰基伸缩振动谱带如图2所示,其IR数据列于表2.从图2可见:糠醛在各种溶剂中都具有两个羰基伸缩振动带,分别位于1 705~1 690 cm-1(I带)和1 684~1 675 cm-1(II带).它们分别归属于O,O-trans糠醛和O,O-cis糠醛中羰基伸缩振动吸收带[18].随着溶剂极性增大,I带和II带均向低波数方向位移,则溶剂化作用使糠醛羰基伸缩振动吸收带出现红移效应.同时,其II带与I带的峰强度之比(Icis/Itrans)也随溶剂极性增大而增大.这表明了随着溶剂极性增大,O,O-trans糠醛向O,O-cis糠醛转化,这与理论计算结果是一致的.
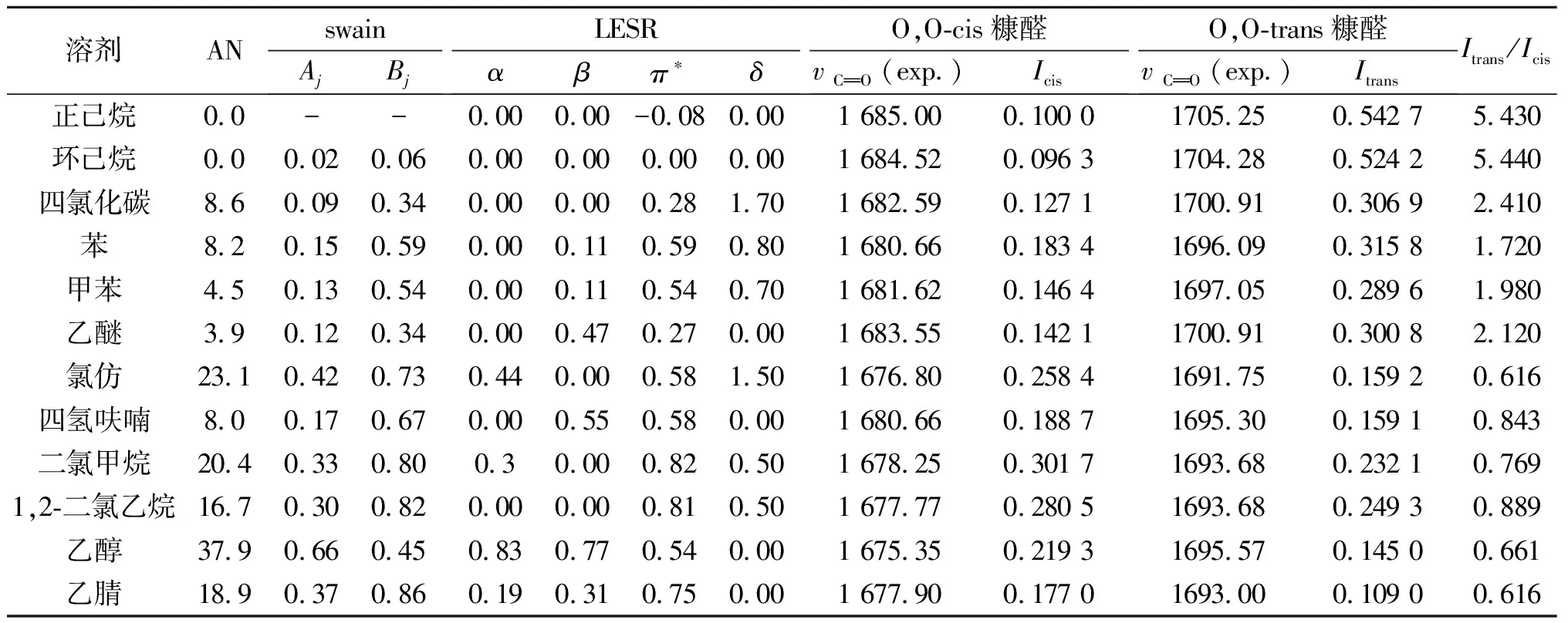
表2 在各种溶液中糠醛羰基伸缩振动带和溶剂参数1)
2.3 羰基伸缩振动频率与溶剂参数相关性分析
Kirkwood,Bauer和Magat以Onsager反应场理论建立了KBM模型用于理论分析溶剂效应对红外光谱位移影响[19],即
(6)
式中:υ0为气相中的振动频率;υ为具有介电常数ε的溶剂中的振动频率;C为由分子维度和振动溶质偶极的电子特性决定的常数;f(ε)=(ε-1)/(2ε+1)称为溶剂极性参数.通过溶剂诱导频率变化与溶剂极性参数f(ε)的相关性分析可知,糠醛的羰基伸缩振动频率与f(ε)值之间呈现离散状态.这表明了无法用溶剂极性参数来解释溶剂—溶质之间的复杂相互作用.
溶剂参数AN值是一种描述电子对接受体(Electron pair accepter, EPA)溶剂的亲电性的经验参数.在12种不同极性溶剂中糠醛羰基伸缩振动频率与AN值之间的关系如图3所示.从图3可见:在不同极性溶剂中,O,O-cis糠醛的羰基伸缩振动频率与AN值之间具有良好的线性相关性,而O,O-trans糠醛的羰基伸缩振动频率与AN值呈离散状态.这意味着O,O-cis糠醛的羰基伸缩振动频率与溶剂的亲电性密切相关,可用于描述溶剂对O,O-cis糠醛的羰基伸缩振动频率位移的影响.而AN值不适用于描述溶剂对O,O-trans糠醛的羰基伸缩振动频率位移的影响.
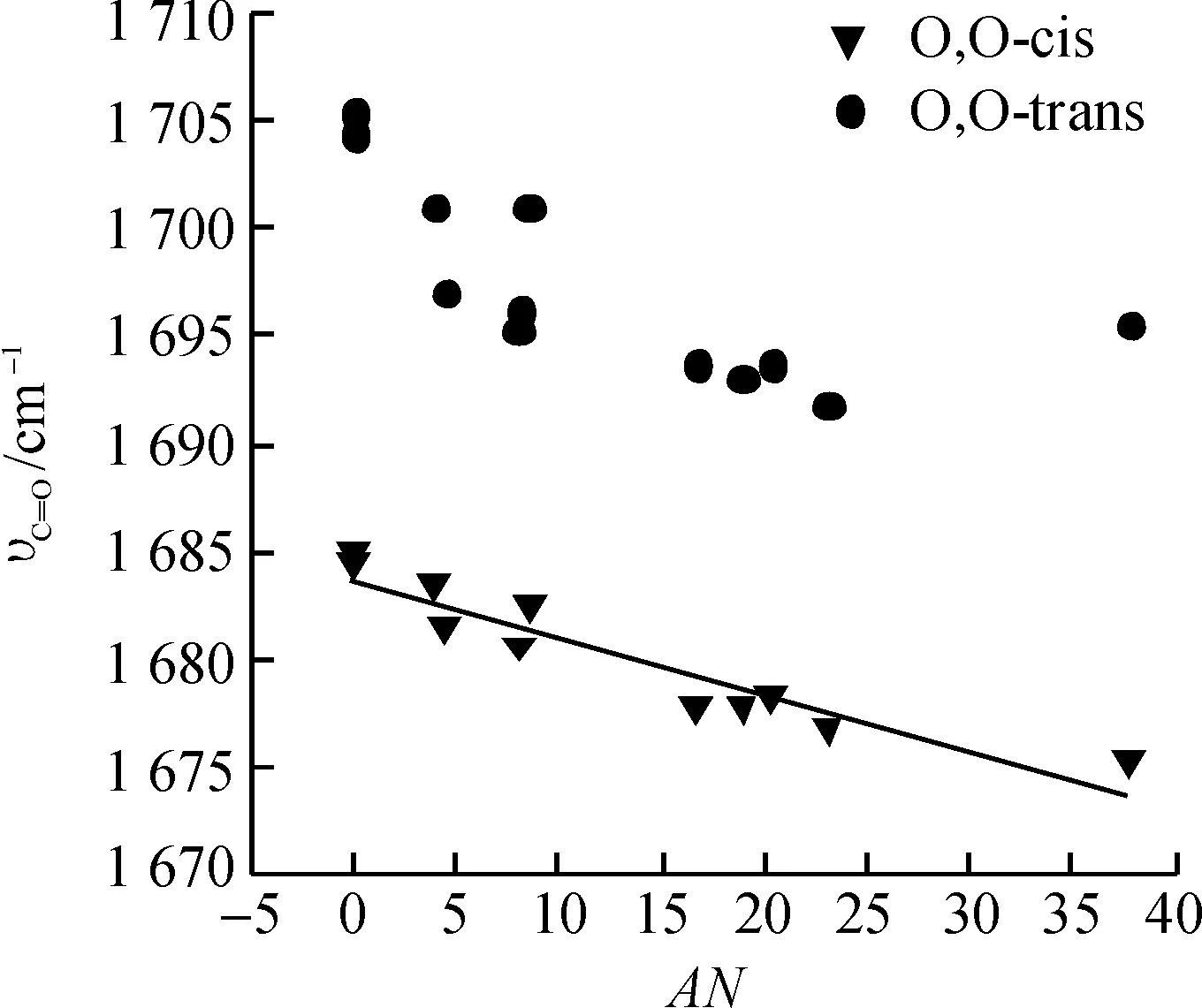
图3 在不同溶剂中糠醛的羰基伸缩振动频率与AN值相关图
Swain等[19]提出了用两个互补溶剂性质参数Aj(溶剂的负离子溶剂化能力)和Bj(溶剂的正离子溶剂化能力)来解释溶剂效应,即
A=A0+ai·Aj+bi·Bj
(7)
式中:i和j分别为溶质和溶剂;ai,bi分别为溶质对溶剂的负离子溶剂化能力和正离子溶剂化能力改变的敏感度.通过二元线性回归分析,糠醛的羰基伸缩振动带的Swain方程具有较好的相关性,即
(8)
(9)
结果表明:对O,O-cis糠醛,ai绝对值大于bi绝对值,对O,O-trans糠醛,ai绝对值小于bi绝对值.这表明了O,O-cis糠醛与溶剂的作用模式不同于O,O-trans糠醛与溶剂的作用.
线性溶剂化自由能关系(Linear solvation energy relationships, LSER)是以溶剂参数α,β,δ和π*来表示线性溶剂化自由能关系的多元参数方程,即
A=A0+s·π*+d·δ+a·α+b·β
(10)
其中:α和β为溶剂接受电子对的能力和溶剂给电子对能力;π*为溶剂极性和极化度效应的量度;δ为对多氯取代的脂肪族溶剂和芳香族溶剂极性和极化度的校正项;s,d,a和b分别为相应参数的敏感度,系数的绝对值越大其敏感度越大,相应参数反映的溶质-溶剂相互作用力越强.糠醛的羰基伸缩振动频率的LSER分别为
υcis=1 684.66-6.912π*-0.131δ-
7.003α+0.460βr2=0.954 8
(11)
υtrans=1 704.45-13.307π*-0.766δ-
0.337α-2.956βr2=0.898 8
(12)
对O,O-cis糠醛,参数的系数绝对值大小次序为:s~a>>b>d,表明了溶剂与O,O-cis糠醛之间的偶极-偶极作用和溶剂接受电子对作用对O,O-cis糠醛羰基伸缩振动频率的影响较为敏感.而对O,O-trans糠醛,参数的系数绝对值大小次序为:s>b>>a>d,表明了溶剂与O,O-trans糠醛之间的偶极-偶极作用和溶剂给电子对作用对O,O-trans糠醛羰基伸缩振动频率的影响较为敏感.
3 结 论
由密度泛函理论(DFT)计算得到的糠醛旋转异构体在不同溶剂中的偶极矩和能量结果表明:在非极性溶剂中,O,O-trans糠醛较O,O-cis糠醛稳定;在极性溶剂中O,O-cis糠醛的稳定性大于O,O-trans糠醛.这与糠醛在不同极性溶剂中的FT-IR实验结果相一致,说明DFT理论适合糠醛溶剂效应的研究.糠醛在不同极性溶剂中的羰基伸缩振动频率与多种溶剂参数的相关性分析结果表明了O,O-cis糠醛和O,O-trans糠醛与溶剂之间的相互作用方式不同,二元溶剂参数Swain方程和多元溶剂参数LSER方程能很好的描述溶剂效应对糠醛羰基伸缩振动频率的影响.
参考文献:
[1] 俞凌翀.基础有机化学[M].北京:高等教育出版社,2001.
[2] GAJEWSKI J J, NGERNMEESRI P. Equilibrium constants between boron trifluoride etherate and carbonyl compounds in chloroform solution[J].Organic Letters,2000,2(18):2813-2815
[3] REICHARDT C. Solvents and solvent effects in organic chemistry[M]. 2nd. New York: Weinheim,1988.
[4] 李郁锦,夏烈,高建荣.吩嗪类化合物的绿色合成研究[J].浙江工业大学学报,2013,41(3):286-288.
[5] 施介华,胡岑晔.γ-丁内酯溶剂效应的红外光谱[J].光谱实验室,2010,27(5):1671-1677.
[6] 施介华,沈丽君.溶液中丙酸红外羰基振动频变与溶剂参数相关性分析[J].浙江工业大学学报,2010,38(6):611-615.
[7] 王东.糠醛产业现状及其衍生物的生产与应用(一)[J].化工中间体,2003(1):16-18.
[8] MOMANY F A, APPELL M, WILLETT J L, et al. B3LYP/6-311++ G**geometry-optimization study of pentahydrates of α-and β-d-glucopyranose[J]. Carbohydrate Research,2005,340(9):1638-1655.
[9] APPELL M, STRATI G, WILLETT J L, et al. B3LYP/6-311++ G**study of alpha-and beta-D-glucopyranose and 1, 5-anhydro-D-glucitol: 4C1 and 1C4 chairs,(3, O) B and B (3, O) boats, and skew-boat conformations[J]. Carbohydrate Research,2004,339(3):537-551.
[10] GECE G, BILGIC S. Molecular-Level understanding of the inhibition efficiency of some inhibitors of zinc corrosion by quantum chemical approach[J]. Industrial & Engineering Chemistry Research,2012,51(43):14115-14120.
[11] CASEY G, WENTWORTH G R, HAMILTON I P, et al. Quantum chemical calculations on solvation effects for selected photoreactive aromatic organic molecules of atmospheric relevance[J]. Computational and Theoretical Chemistry,2011,965(2):346-352.
[12] SISKOS M G, KONTOGIANNI V G, TSIAFOULIS C G, et al. Investigation of solute-solvent interactions in phenol compounds: accurate ab initio calculations of solvent effects on 1H NMR chemical shifts[J]. Organic & Biomolecular,2013,11:7400-7411.
[13] MILANI A, CASTIGLIONI C, DI DEDDA E, et al. Hydrogen bonding effects in perfluorinated polyamides: an investigation based on infrared spectroscopy and density functional theory calculations[J]. Polymer,2010,51(12):2597-2610.
[14] PERRIN D D, ARMATEGO W L F. Purification of laboratory chemicals[M]. 3nd. Oxford: Butterworth-Heinemann,1988:16-17.
[15] ALLEN G, BERNSTEIN H J. Internal rotation VIII. The infrared and raman spectra of furfural[J]. Canadian Journal of Chemistry,1955,33:1055.
[16] HATCHOOTAH A, PONNADURAI R. Rotational barrier and thermodynamical parameters of furfural, thiofurfural, and selenofurfural in the gas and solution phase : theoretical study based on density functional theory method[J]. Molecular Physics,2008,106:175-185.
[17] 程能林.溶剂手册[M].2版.北京:化学工业出版社,1994.
[18] 贾廷见,李朋伟,尚志国,等.糠醛分子的拉曼光谱与红外光谱研究[J].光散射学报.2007,19(1):1-5.
[19] KIRWOOD J G. On the theory of optical rotatory power[J]. Journal of Chemical Physics,1937,5(6):479-492.
[20] SWAIN C G, SWAIN M S, POWELL A L, et al. Solvent effects on chemical reactivity. Evaluation of anion-and cation-solvation components[J]. Journal of the American Chemical Society,1983,105(3):502-513.
