基于改进蚁群优化算法的车间布局优化

葛安华，姚向楠，张玉巧

(东北林业大学 工程技术学院，哈尔滨 150040)

随着市场竞争的加剧和生产方式的变革，原有的设施布局渐渐不适应要求，迫使企业对已有系统、人员和设施进行重新评估和认识，这使得布局的问题逐渐显现出来，人们也越来越重视如何设计出更高效的布局。但布局问题是一个及其复杂且矛盾的优化问题，目前一些学者提出的布置模型还不够完善，其求解算法也有许多不足。改进的蚁群优化算法是在克服蚁群优化算法缺点的基础上发展而来，应用范围几乎遍及各个领域[1]。鉴于此，本文将采用一种改进的蚁群算法来求解车间布局的优化问题。

1 车间布局问题的二次分配建模

1957年Koopamans和Beckmann为彼此间有物料流动的设施的位置问题提出了二次分配问题(QAP)[2]。为简化该模型做如下假设：

(1)确定数量的需要布置在矩形区域中的矩形设施。

(2)设施的位置相互之间不能重叠，且不能超出矩形区域。

(3)设施间的距离度采用直角距离进行计量。

(4)不同设施间单位物流量搬运单位距离所需费用相同，且为1。

以总搬运成本Z最小为目标，现有n个设施和n个位置，每个设施要求布置在一个不同位置上，假如设施i被布置在位置点k上，设施j被布置在位置点h上，设施i与j之间流量用fij来表示，位置点k与h之间的距离用dkh来表示。

那么QAP的数学模型可表示为

(1)

式中：xik、xih为决策变量，如果设施i布置在位置点k上，则xik取值为1，否则xik取值为0。公式(2)为其约束条件。

。(2)

2 改进蚁群优化算法的求解

蚁群优化算法(ACO)已成为解决各种组合优化问题的最有效的算法之一[3-12]，根据二次分配的特点，蚁群优化算法适用于解决二分配问题。但传统的蚂蚁算法采用固定的信息素增减来进行信息素更新，使得这种算法容易出现收敛速度慢、陷入局部最优、运算时间长等现象[13]。为了解决这个问题，Stutzle和Hoos对此提出了两点改进，一是把路径上的信息素浓度的大小限制在[τmin,τmax]范围之内，二是对信息素强度更新提出了新的更新规则，这就是最大最小蚂蚁系统(MAX-MIN Ant System，MMAS)。本文将运用最大最小蚂蚁系统来求解车间布局QAP模型。

2.1 问题图形表示

根据目标函数和约束条件，车间布局问题的构件图设计如图1所示。从而构成了n个设施选择n个位置的决策问题。每个节点{rij|i=1,2,…n;j=1,2…n}表示设施i选择布局的位置j。这样共有nn向量将节点从第1个位置连接到第n位置。

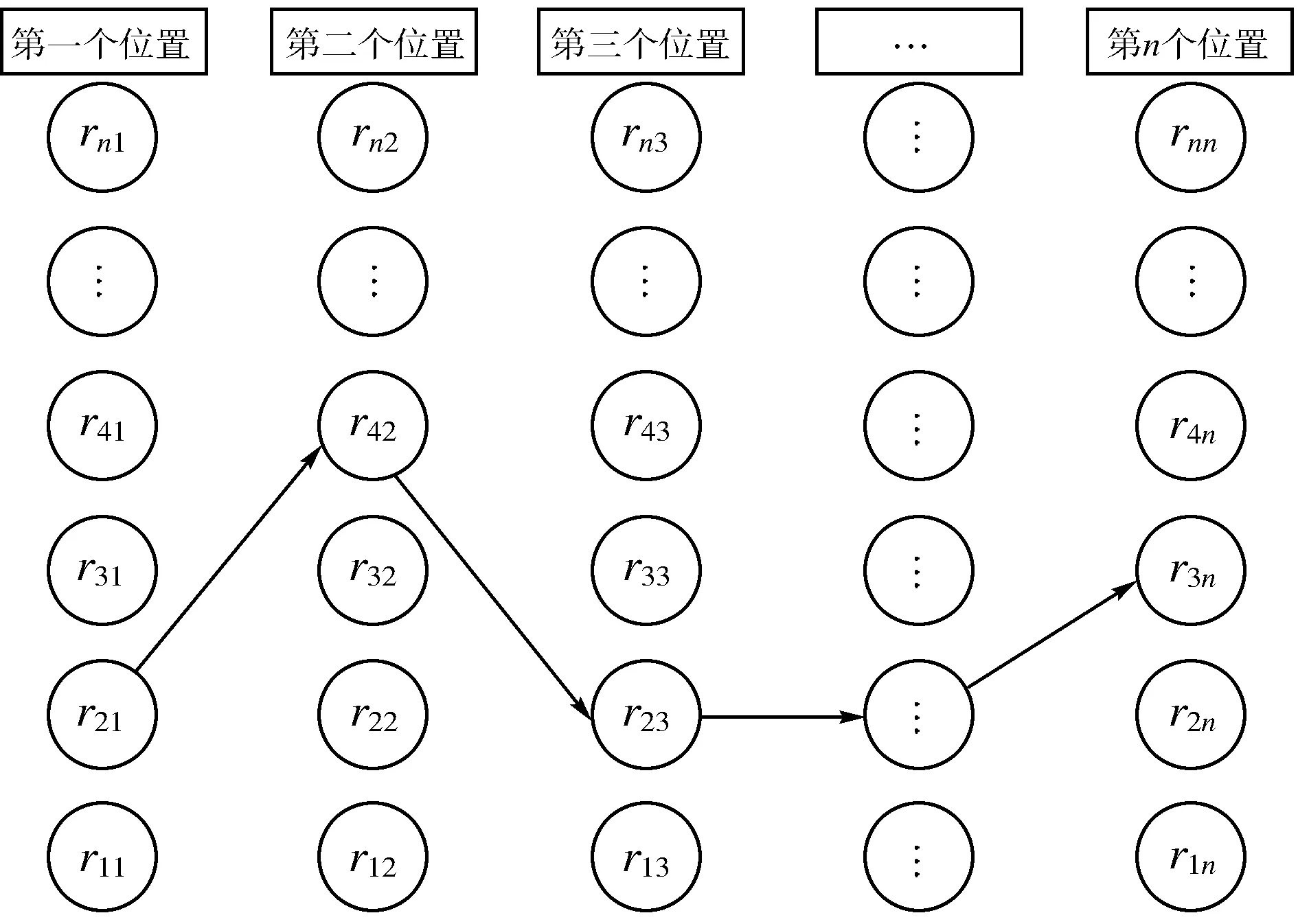
图1 车间布局的构建图

2.2 蚂蚁的路径选择

蚂蚁在各个节点上游走，并留下不同的信息素的浓度，以此来影响下一批蚂蚁选择的移动方向。令τij(t)为t时刻各个节点上信息素的浓度大小，初始时刻节点上的信息素浓度为τ0。生成的Nant只蚂蚁被放在图1第一个位置的各个节点上，然后每一只蚂蚁根据信息素和启发式信息独立的选择下一位置的某个节点，t时刻，处于节点rij时的蚂蚁k选择下一位置节点rz(j+1)的概率公式为：

(3)

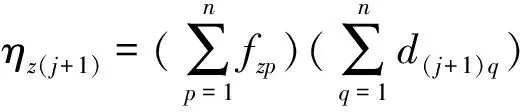
3 车间布局的蚁群算法

3.1 车间布局蚁群算法的描述

在初始化数据、参数和信息素之后，设NCmax为最大迭代次数，ACO算法反复在主循环中迭代，当Nant只蚂蚁都迭代完成，得到了Nant组解初始解，然后，通过局部搜索法对初始解进行优化，最后更新信息素矩阵。总共分为三大步骤，具体运行如下。

3.1.1 初始解

(1)把初始化禁忌表的值设为零。

(2)fork=1toNant，按照公式3概率公式计算选择下一个位置的节点，如蚂蚁没走到最后一个位置，将其所选择的节点加入蚂蚁k的禁忌表，结束。

(3)当蚂蚁第k=Nant时，每一只蚂蚁都已经建立了初始解。否则返回(2)。

3.1.2 局部搜索优化

本文运用的局部搜索方法是运用传统的2-选择交换和一种新的交换方法相结合的形式来计算的，结果表明其改善方法更优一些。运用局部搜索法对初始解优化的步骤为：

(1)fork=1，局部搜索次数设定为1。

(2)随机产生两个要交换元素的位置，对其进行交换。

(3)交换后目标函数值的新解小于初始解时，实施交换，否则不进行交换。

(4)当局部搜索次数为n次，fork=Nant时，完成了对所有初始解的局部搜索。

3.1.3 信息素更新

MMAS对信息素的大小值施加限制，控制在范围[τmin,τmax]，如果更新后的信息素大于τmax或者小于τmin，强令其值τmax或者为τmin。当所有蚂蚁都完成局部搜索后，将进行信息素更新。信息素更新分为信息素的挥发和信息素的释放，具体规则为：

τij(t+1)=(1-ρ)τij(t)+Δτij(t)。

(4)

(5)

(6)

式中：ρ表示挥发因子；1-ρ则为残留因子；Cbest为当前迭代最优解或者是至今最优解。信息素的释放只对系统产生的最优解和当前最优解，其他解Δτij(t)=0。

具体步骤为：

(1)产生随机数，判断其解是否为至今最优还是当代最优，计算信息素相应的释放量Δτij(t)。

(2)对信息素矩阵进行信息素进行挥发，然后计算更新之后的信息素τij(t+1)。

(3)判断信息更新之后的量是否在[τmin,τmax]之内，若不在则按信息素更新规则更改。

根据上面三大步骤的不断循环和分析，最终将获得车间的最优布局方案。下面给出一个简单的应用范例。

3.2 实例应用

一个总面积为35 m×20 m的生产车间，车间有12个生产单元，现以最小化物料运输成本为目标函数，建立该车间的QAP模型，对该车间的布局进行优化。现根据QAP模型要求把车间区域重新划分，由于有12个生产车间，则划分为12个面积相等的区域，按照三行进行布置。现有各个生产单元之间的物流流量表1。区域之间的距离运用距心之间的直角距离来计算，相邻之间为一个单位，这样就构造了一个距离矩阵见表2。车间的原来的布局方案为R=(D，H，C，I，F，A，L，J，G，B，E，K)，如图2所示。

该布局方案的物料的搬运成本为

(7)

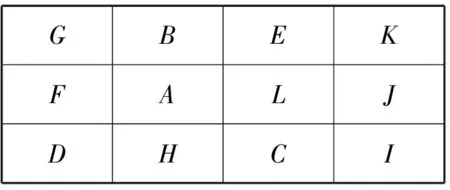
图2原始布置方案

Fig.2 The original layout plan

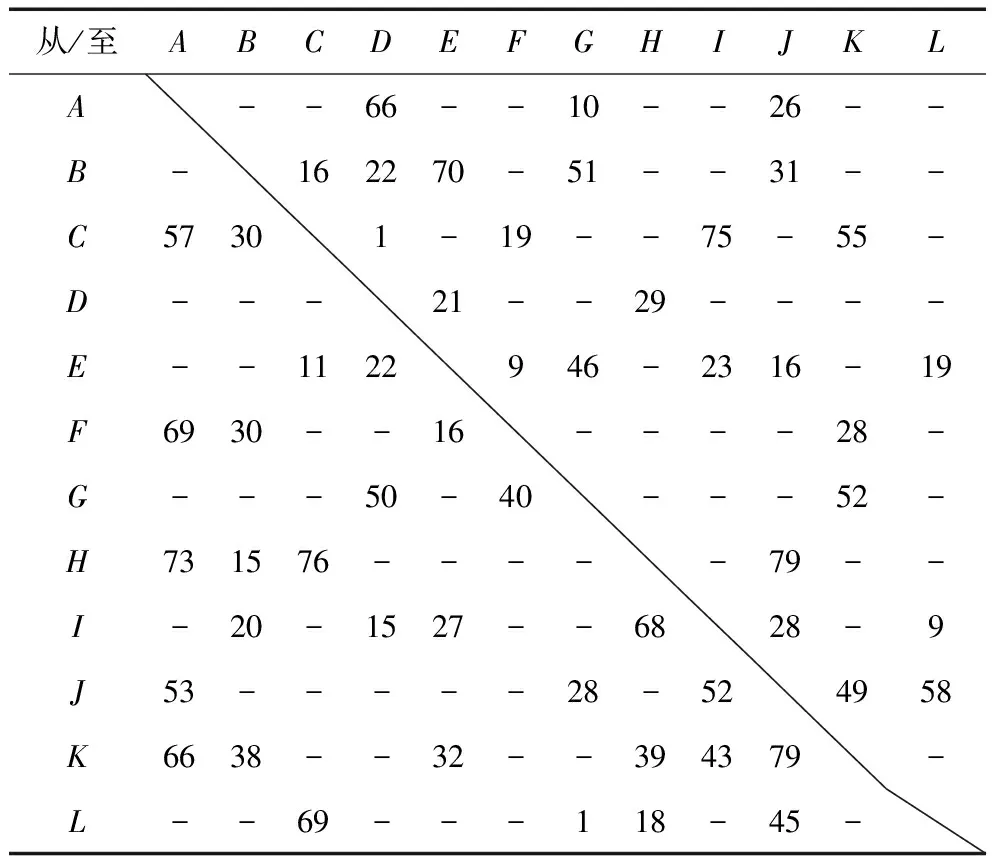
表1 各单元之间的物流量矩阵 kg

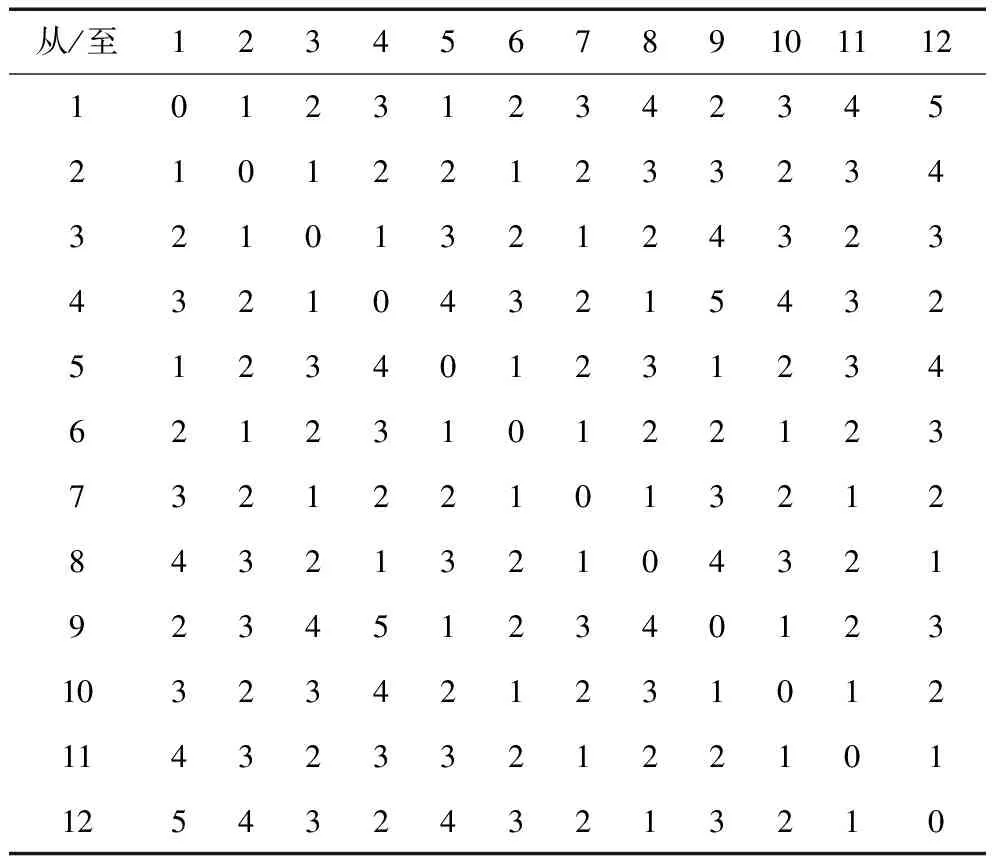
表2 各区域间的距离矩阵表 m

运行环境：PC机，内存为2G，操作环境为win7，开发VC++6.0实现，程序中用到的参数设置为Nant=12，NCmax=12，α=1，β=2，ρ=0.05，τmax=2，τmin=0.4，Q=1000，Cbest=5，τ0=2，n=30。运行结果，得出最优的布置方案为R=(E，B，I，C，G，K，J，H，D，F，A，L)。相应的布置如图3所示。该布置方案的物料的搬运成本为3680。

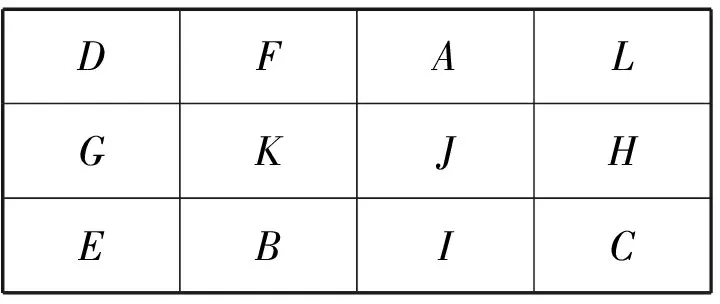
图3最优布置方案

Fig.3 Optimal layout scheme

显然，和原布局方案进行比较，新方案高潜在物流量的生产单位分配到具有低潜在距离的位置上，所以在物料搬运的成本上更低。

4 结论和讨论

本文根据车间布局优化的最小物流费用原则，建立了布局优化的QAP数学模型，针对QAP的特点，提出了一种改进的蚁群优化算法来对其进行求解，该算法强调对最优路径的开发，并且对路径上信息素浓度的大小进行了限制，避免了搜索的停滞；同时对信息素强度更新提出了新的更新规则，并且融合局部搜索的方法，使得改进后的蚁群算法解的性能得到较大提高。结合具体实例，并通过VC++6.0编程来实现求解，结果表明，新布局方案物料搬运成本要比原布局方案节约10%，验证了改进的蚁群优化算法对布局优化的QAP数学模型的求解是可行且有效的。

不可否认的是蚁群优化算法是一个复杂的系统，它的行为受到参数、宏观算法部件和问题特性等多方面影响，本文使用的改进的蚁群优化算法一定程度上克服了它的一些缺陷，但如何最有效的发挥算法的性能还需做进一步研究；另外，本文求解的车间布局问题是静态的车间设施平面布局，对于更复杂的车间布局问题也还需做进一步研究和探讨。

【参 考 文 献】

[1]桑国珍，李智勇.蚁群算法研究与应用[J].内江科技，2009(8)：33-34.

[2]Lari M B.Layout designs in cellular manufacturing[J].European Journal of Operational Research，1999，112：258-272.

[3]张利城，吴金卓，何 荣.基于循环取货模式的车辆路径优化研究[J].森林工程，2013，29(4)：87-89.

[4]鲁 强，陈 明.平面布局的蚁群算法[J].计算机应用，2005，25(5)：1119-1121.

[5]范 文，余隋怀.蚁群算法求解人及布局优化问题[J].机械科学与技术，2004，14(4)：423-427.

[6]鲁 强，陈 明.平面布局的蚁群算法[J].计算机应用，2005，25(5)：1019-1021.

[7]Al-Attar A.A hybrid GA-heuristic search strategy[J].Al Expert USA，1994，9(9)：34-37.

[8]Komarudin K.Applying ant system for solving unequal area facility layout problems[J].European Journal of Operational Research，2010，202：730-746.

[9]王家善.设施规划与设计[J].工业工程，1998，1(1)：11-14.

[10]吴永忠.面向大规模定制的生产线优化设计系统的研究与开发[D].广州：广东工业大学，2004.

[11]葛安华，周晏明，李权章.改进遗传算法求解作业车间提前/托期调度问题[J].森林工程，2013，29(3)：138-141.

[12]詹玉洪.求解车辆路径问题的混合蚂蚁系统[J].计算技术与自动化，29(1)：138-141.

[13]倪庆剑，邢汉承.蚁群算法及其应用研究[J].计算机应用与软件，2008，25(8)：12-15.