电磁波反射折射中能量守恒关系的分析
2014-08-23张建华
张建华,黄 冶
(电子工程学院,安徽合肥 230037)
电磁波对平面边界的入射、反射和折射是“电磁场与电磁波”课程中一项重点内容[1-5],功率流密度即坡印廷矢量是反映电磁能量流动的一个重要物理量[6]。当均匀平面波垂直入射于平面边界上时,入射波的功率流密度减去反射波的功率流密度,等于折射波的功率流密度,即满足能量守恒定律。但是,我们经常发现有些学生将垂直入射的这种能量守恒关系直接应用于斜入射的情况,导致错误。
本文以全折射情况为例,分析了将垂直入射的能量守恒关系直接应用于斜入射情况时所导致的错误结果,并对其原因进行解释。笔者以三种不同机理推导了电磁波斜入射情况下的能量守恒关系,这三种机理分别是:①功率流密度的矢量性;②分界面单位面积上的功率流密度;③定义功率反射系数和功率折射系数。最后从射线管的角度分析了全折射时的能量守恒关系。我们采用多种机理分析电磁波斜入射情况下的能量守恒关系,有助于学生融会贯通,深入理解电磁波斜入射时的能量守恒关系。
1 均匀平面波垂直入射的能量守恒

均匀平面波垂直入射至两种介质平面分界面时,由边界条件可得反射系数R和折射系数T为式中,η1和η2分别为媒质I和媒质Ⅱ两种介质的波阻抗。利用上式可以证明入射的功率流密度Si和折射的功率流密度St有下列关系:

该式表明:在媒质I,入射波传播的功率减去反射波向相反方向传播的功率等于向媒质Ⅱ折射的功率,符合能量守恒定律。我们在教学中发现,式(2)和式(3)在某些情况下将会引发学生对有关能量守恒定律的歧义,理解困难。一种情况是:当η2>η1时,由式(2)可得折射系数为

这说明折射波的电场强度大于入射波的电场强度。乍一看,似乎违反了能量守恒定律。实则不然,因为折射波的功率流密度为

另一种情况是:如果将式(3)直接应用于斜入射情况,会得到矛盾的结果。一个最简单的例子是平行极化波发生全折射的情况,此时反射系数=0,由式(3)应有Si=St。然而,利用折射系数与反射系数的关系式:

可得全折射时的折射系数为

将此结果代入媒质Ⅱ中的功率流密度公式可得

由上式可见,St≠Si,即式(3)不再成立。这说明斜入射时,假如仍然按折射功率密度St=Si(1-R2)处理,会得出错误的结果。
那么,为什么不能将垂直入射条件下的能量守恒关系式(3)直接应用于斜入射情况呢?这可以从以下两个方面进行解释。
(1)功率流密度是有传播方向的,是矢量。斜入射时,入射波功率流密度、反射波功率流密度和折射波功率流密度的传播方向不在同一条直线上;
(2)功率流密度表示的是通过单位面积的传播功率,该单位面积是指垂直于传播方向上的单位面积,当斜入射时,该单位面积在边界面上对应的面积发生变化,不再是单位面积了。
2 均匀平面波斜入射时的能量守恒
2.1 矢量形式的能量守恒
我们现在讨论均匀平面波对平面边界的斜入射,以垂直极化波斜入射到两种非铁磁性理想介质分界面为例,如图1所示。

图1 平面波斜入射示意图
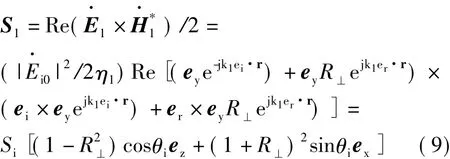
其中,R⊥为垂直极化波的反射系数,其他变量如图1所示。按照能量守恒定律,该功率流进入媒质Ⅱ,即为折射波的功率流密度,方向是折射波方向,下面对此进行证明。
折射波的功率流密度矢量为

其中,St为折射功率流密度的模值,T⊥为垂直极化波的折射系数,θt为折射角。由边界条件可得垂直极化波的反射系数和折射系数为
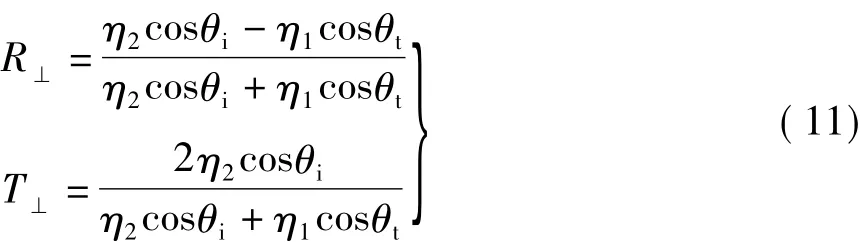
将以上两式分别代入式(9)和式(10),可得

即有

上式或其具体表达式(12)即为矢量形式的能量守恒关系。
2.2 分界面单位面积上的能量守恒
对于斜入射情况下式(3)不成立的原因,本文给出另一种形式的能量守恒关系。
入射波功率流密度Si的模值表示的是在与入射方向垂直的单位面积上传播的功率,而不是入射到分界面单位面积上的功率。入射到分界面单位面积上的功率是

反射波和折射波每秒从分界面单位面积带走的能量分别是
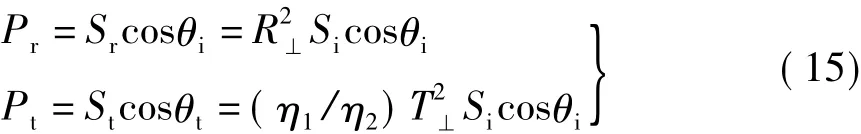
将反射系数和折射系数公式(11)代入上式得

上式表明:入射到分界面单位面积上的功率减去反射波每秒从分界面单位面积带走的能量,等于折射波每秒从分界面单位面积带走的能量,即满足能量守恒定律。该能量守恒关系也可写为

与第2.1节的结果比较,上式即是式(13)的z分量相等。
2.3 功率反射系数和折射系数形式的能量守恒
下面再从功率反射系数和功率折射系数的角度来分析能量守恒关系。定义功率反射系数和折射系数分别为
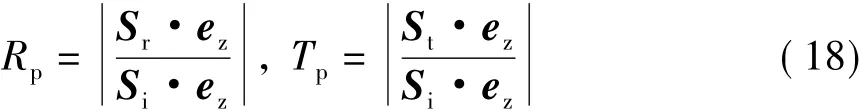
可以证明


以下分两种情况进行分析,一种是入射波电场矢量垂直于入射面的垂直极化波,另一种是入射波电场矢量平行于入射面的平行极化波。
(1)对于垂直极化波,可将式(20)代入式(11),易得
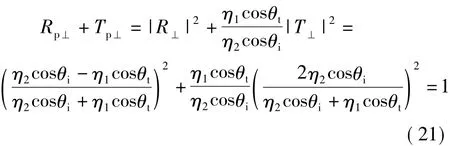
该式表明:在z轴方向上,反射功率流密度与透射功率流密度之和等于入射功率流密度。该式与第2.1节和2.2节表述的能量守恒关系在本质上是一致的。
(2)对于平行极化波,反射系数和折射系数分别写为

可得

上式即为平行极化波在z轴方向上的功率反射系数和折射系数形式的能量守恒关系。如上所述,该式本质上与前面的分析是一致的,不过是从不同的角度予以证明而已。
图2给出了当η1/η2=2时,垂直极化波和平行极化波的功率反射系数和折射系数的数值计算结果,同样表明了Rp+Tp=1。从图2(b)中还可以看到全折射时的情况,当入射角等于63.4°时,功率反射系数等于零,对应的功率折射系数等于1。
2.4 全折射时的能量守恒关系
在本文第一部分中曾以全折射情况为例,分析了不能直接将垂直入射情况下的能量守恒关系应用于斜入射,此时正确的能量守恒关系见上述第2.1节至2.3节的分析。我们把与等相位面垂直的电磁波传播轨迹称为射线,由一簇射线组成的能量传播通道称为射线管,沿一个射线管的总能流是常数。下面再从射线管的角度来分析全折射时的能量守恒关系。

图2 功率反射系数和功率折射系数
我们知道,功率流密度表示的是在垂直于传播方向的单位面积上传播的功率。在媒质Ⅰ中垂直于入射方向的单位面积上传播的入射功率为||2/2η1,如图 3 所示。
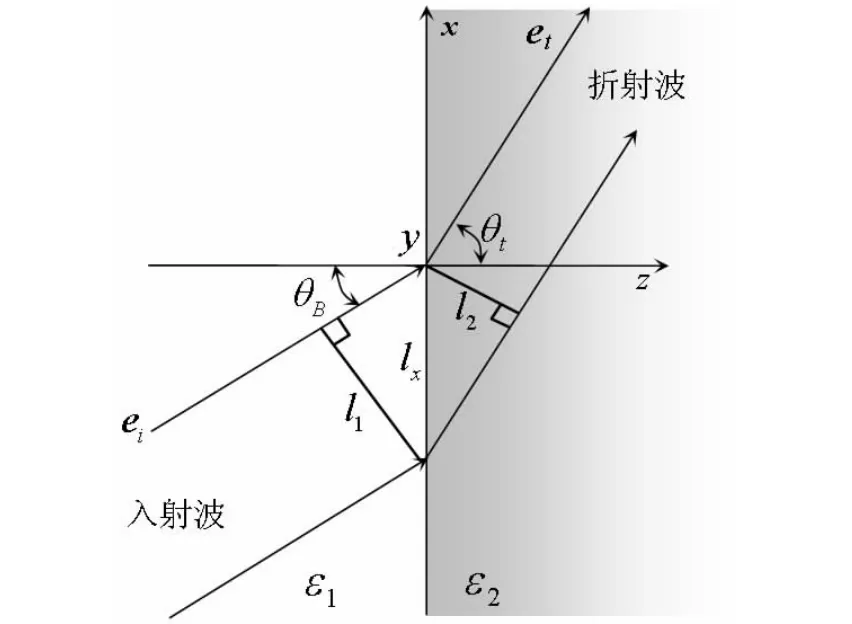
图3 发生全折射时的几何关系示意图
设该单位面积在xz平面内边长为l1,在y轴方向边长为ly(为了简洁,图中没有标示ly),l1在z=0的边界面上的对应的长度lx为

lx在垂直于折射波传播方向的横截面内对应的长度l2为
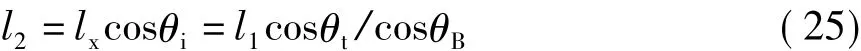
按照能量守恒定律,发生全折射时,媒质Ⅰ中单位面积l1ly上流过的能量应该等于媒质Ⅱ中面积l2ly上流过的能量,该结论可以证明如下。
在媒质Ⅱ中垂直于折射方向的单位面积上传播的折射功率为|E·i0|2/2η2,则
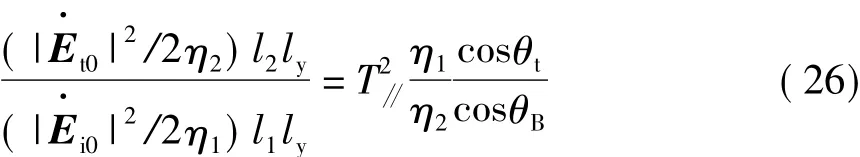
利用式(7),计及非铁磁性媒质的布儒斯特角和相应的折射角满足关系θt=π/2-θB,代入上式可得

这样就从射线管的角度诠释了全折射时的能量守恒关系。
3 结语
本文从四个不同视角分析了电磁波斜入射情况下的能量守恒关系,得到了能量守恒关系式,即式(12)和式(13)、式(16)和式(17)以及式(19)和式(27)。这些表达式有助于我们深入理解斜入射时能量守恒关系的本质,使我们能够触类旁通地灵活运用能量守恒关系。
[1] 钟顺时.电磁场基础[M].北京:清华大学出版社,2006
[2] 毕德显.电磁波理论[M].北京:电子工业出版社,1985
[3] 孙玉发等.电磁场与电磁波[M].合肥:合肥工业大学出版社,2006
[4] Kong J Au.Electromagnetic wave theory[M].北京:高等教育出版社,2002
[5] 郭琳,张明,洪伟.电磁场教学中的电磁波斜入射问题讨论[J].南京:电气电子教学学报,1999,21(4):22-24
[6] 杜晓燕,杨明珊,安娜.关于坡印廷矢量教学的几点思考[J].南京:电气电子教学学报,2012,34(6):118-120
