Sedumi软件包在教学和科研中的应用

蒋俊正，周 芳

(桂林电子科技大学1信息与通信学院，2.生命和环境科学学院，广西桂林 541004)

Sedumi软件包最早由加拿大Mcmaster大学的研究人员于上世纪90年代后期提出，它基于Matlab语言开发主要用于求解半定规划问题［1］。在“数字信号处理”和“最优化理论与方法”等电子信息类课程教学和科研中，很多问题都可以归结为某种优化问题，可以直接或间接地使用Sedumi软件包进行有效求解。

1 Sedumi标准形式下的使用

半定规划问题可以直接使用Sedumi软件包进行求解［2-4］。下面笔者分别介绍线性规划、二阶锥规划和半定规划问题的标准形式以及求解的Matlab代码。

1)线性规划

用于求解问题(1)的Matlab代码为

［x，y，info］=sedumi(A，b，c)

代码中向量y是最优解，info包含了一些辅助信息，比如求解耗时等。

2)二阶锥规划

用于求解问题(2)的Matlab代码为

K.1=m;

K.q=q;

［xs，ys，info］=sedumi(At，bt，ct，K);

代码中m等于矩阵D的行数，即线性约束的个数。代码参数为

3)半定规划

式中，矩阵Fi，i=0，…，p为对称矩阵。用于求解问题(4)的Matlab代码为

K.S=size(F0，1);

［x，y，info］=sedumi(At，bt，ct，K);

info代码中参数为

由于Sedumi软件包在求解中采用了对偶理论，因此求解效率很高。

2 Sedumi非标准形式下的使用

然而在实际中，很多的优化问题并不具备上述的三种标准形式，导致Sedumi软件包的使用并非如上述那么直观。因此，如何将非标准形式转化为标准形式，是有效利用Sedumi的关键所在。

我们以二次规划问题转化为二阶锥规划问题为例进行说明。二次规划问题是指目标函数是关于优化变量的二次函数、约束是线性函数的优化问题:

其中，矩阵A是正定的。引入辅助变量 ，问题(6)可等价为

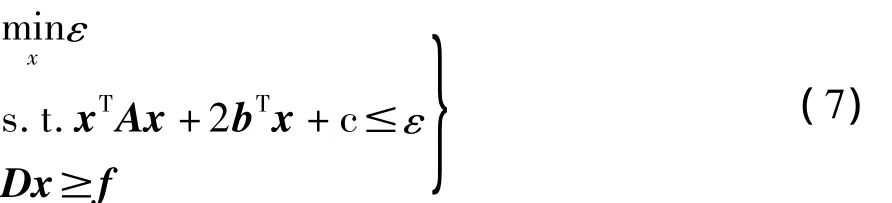
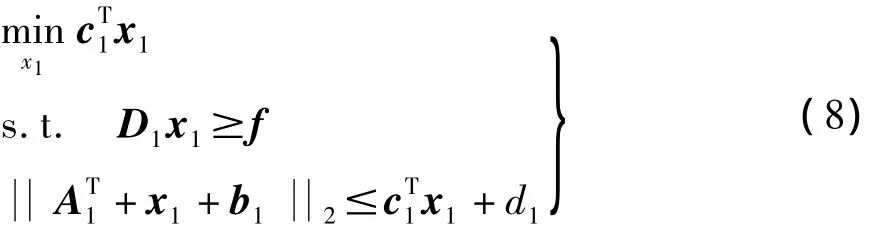
式中代码参数为

式中m为x的长度，N为D的行数。

3 Sedumi软件包的应用举例

FIR数字滤波器的设计问题可以归结为一个优化问题［5-7］。通常，滤波器的性能指标包括:阻带衰减和通带平坦性。一个性能优良的滤波器应该具备阻带衰减高且通带平坦，数学描述为

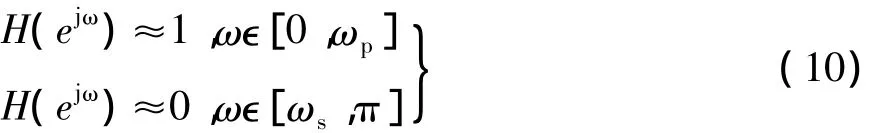
式中，ωp和ωs分别为低通滤波器的通带和阻带的截止频率。假定一个线性相位的低通滤波器的系数满足:

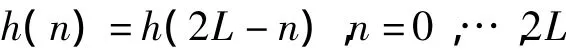
其频率响应可表示为

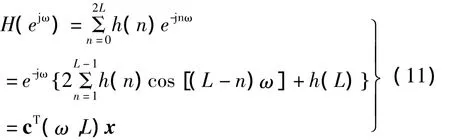
式中

设计阻带衰减高且通带平坦的滤波器可以归结为如下优化问题:

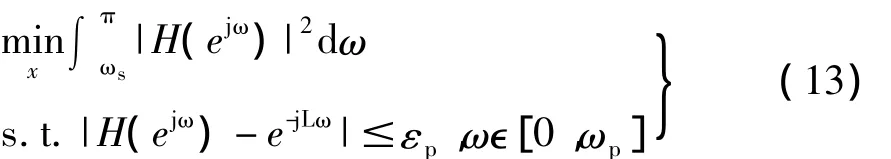
式中εp为容许误差。将式(11)代入式(13)，并对区间［0，ωp］进行等间隔离散化 ωk=kωp/K，k=0，…，K，可得

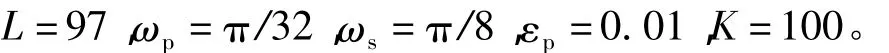
设计所得的滤波器的冲激响应和幅度响应如图1所示。可以看出，该滤波器具备良好的频率特性，即通带平坦、阻带衰减高。

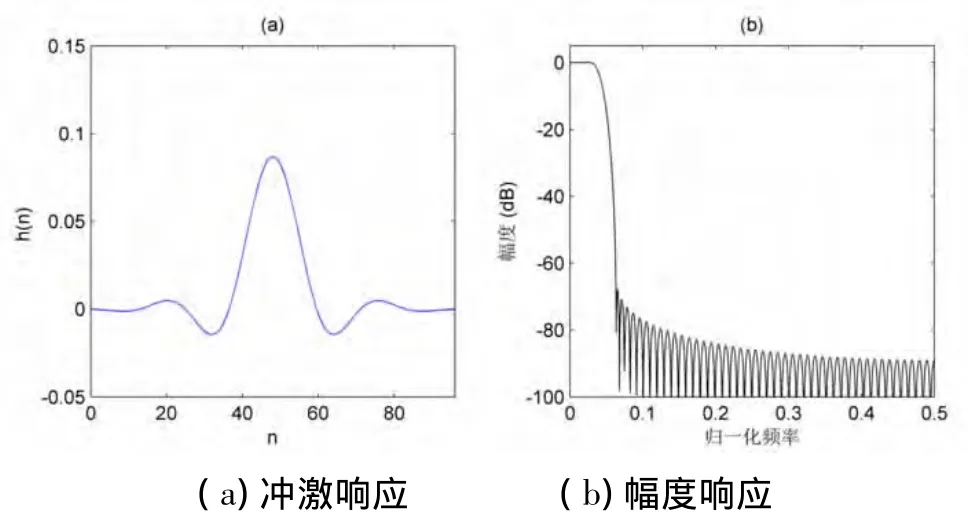
图1 Sedumi软件设计所得的滤波器

4 结语

本文首先介绍Sedumi优化软件包求解问题的三种标准形式和相应的Matlab代码，然后以二次规划为例说明如何将非标准形式转化标准形式，最后将Sedumi应用于数字滤波器设计问题求解。在教学和科研中出现的非标准形式优化问题，如何进行转化，并采用Sedumi求解仍需进一步探讨和研究。

［1］ J.F.Sturm.Using SeDuMi 1.02，a MATLAB toolbox for optimization over symmetric cones［J］.Optimization methods and software，1999，11(1-4):625-653.

［2］ 袁亚湘，孙文瑜.最优化理论与方法［M］.北京:科学出版社，1997.

［3］ D.P.Palomar，and Y.C.Eldar.Convex optimization in signal processing and communications［M］.Cambridge University Press，2010.

［4］ Z.Q.Luo，and Y.Wei.An introduction to convex optimization for communications and signal processing［J］.IEEE Journal on Selected Areas in Communications，2006，24(8):1426-1438.

［5］ 陈怀琛，王朝英，高西全等.数字信号处理及其 MATLAB实现［M］.北京:电子工业版社，1998.

［6］ 郭建涛.“数字信号处理”课程的Matlab教学研究［J］.电气电子教学学报，2010，32(3):117-119.［7］ T.N.Davidson，Z.Q.Luo，and J.F.Sturm.Linear matrix inequality formulation of spectral mask constraints with applications to FIR filter design［J］.IEEE Transactions on Signal Processing，2002，50(11):2702-2715.