一题多解谈高考采分点

江苏省常州市北郊高级中学 (邮编：213031)

2014年江苏高考阅卷工作早已结束，全省数学包含空白卷约40万份,填空均分51.5,第15题11.5分；第16题12.56分；第17题7.6分；第18题5.5分；第19题4.9分；第20题：2.6分.平均96.1分.今年江苏数学卷整体偏简单，但18题虽然不难，但该题是多年以来解法最多的一题，初步总计15种解法.给阅卷工作带来前所未有的挑战，下面通过该题的评分标准总结平时教学注意点，虽然每年评分标准不同但仍有大体不变之处供教学参考.

1 试题呈现 如图：为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区，规划要求，新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上，并与BC相切的圆，且古桥两端O和A到该圆上任一点的距离均不少于80m，经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处，(OC为河岸)，

(1)求新桥BC的长；

(2)当OM多长时，圆形保护区的面积最大？

2 主要解法踩分点说明

本小题主要考查直线方程、直线与圆的位置关系和解三角形等基础知识，考查建立数学模型及运用数学知识解决实际问题的能力，满分16分第一问大致有两类解法，一类解析几何建系；另一类平面几何做辅助线配合解三角形，第二问大致两种解法.踩分以点为主有就给分没有零分不给同情分.

解法1

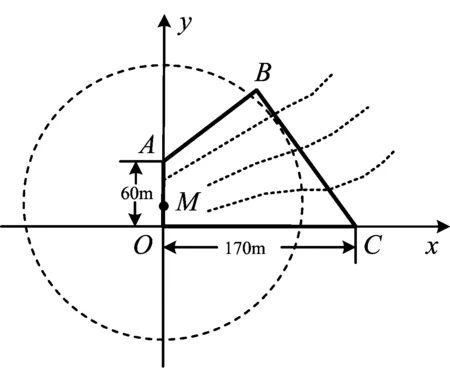
如图，以O为坐标原点，OC所在直线为x轴，建立平面直角坐标系xoy.

由条件知A(0, 60)，C(170, 0)，

注：两个斜率得2分缺一不得分.

解得a=80，b=120.

得出B点坐标，得2分.

因此新桥BC的长是150 m.

解法2

AB、BC直线方程同时对得2分；AB、BC解交点(80，120)得2分.

解法3AB直线方程求对得2分;写出点C到AB的距离公式得2分;结果2分.

解法4

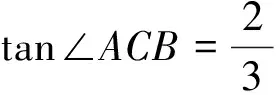
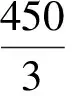
解法5

(1)如图，延长OA、CB交于点F.

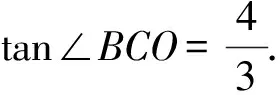
因为OA=60,OC=170，

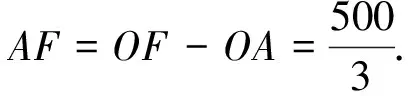
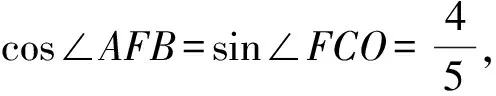
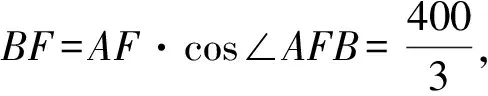
因此新桥BC的长是150 m.

其他解法如上图类比给分.

(2)解法1

设保护区的边界圆M的半径为rm,OM=dm,(0≤d≤60).

求对BC直线方程不管什么形式得2分，若没求BC但第一问有不扣分，若没有则不得分.

由于圆M与直线BC相切，故点M(0，d)到直线BC的距离是r，

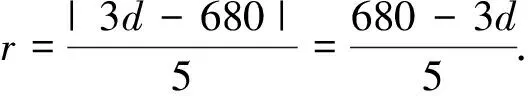
得到r与d关系即使不去绝对值也得3分

因为O和A到圆M上任意一点的距离均不少于80 m,

解得10≤d≤35.

此得分点称建模得分点，和上面没有逻辑关系，是独立的逻辑链容易踩到分.可惜的是每个同学都有能力拿但是没拿到，只要同时写出两个不等式，哪怕r、d代入错误，不重复扣r、d的分仍然可以拿到3分，但两个不等式必须要对,缺一或无等号没分.

所以当OM= 10 m时，圆形保护区的面积最大.

最终结果及答2分，如果没有答只要有单位m也可以，若没有答扣1分.

解法2

(2)设保护区的边界圆M与BC的切点为D，连接MD，则MD⊥BC，且MD是圆M的半径，并设MD=rm，OM=dm(0≤d≤60).

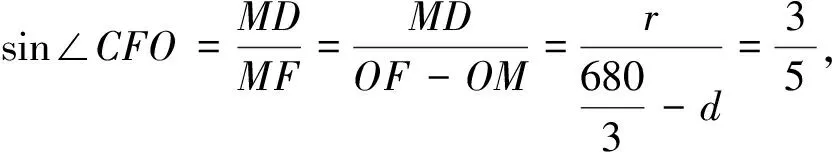
因为O和A到圆M上任意一点的距离均不少于80 m,

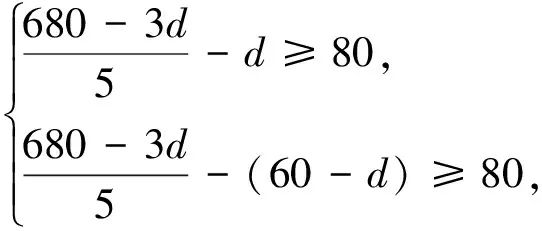
最终结果及答2分，如果没有答只要答案有单位m也可以，若没有答扣1分.

3 本题踩分点分析

(2)设保护区的边界圆M的半径为rm,OM=dm,(0≤d≤60).

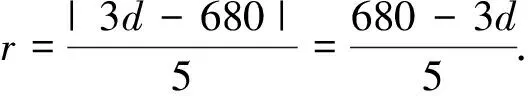
因为O和A到圆M上任意一点的距离均不少于80 m,

这样做的学生很多虽然都没有解出结果但也得了14分，所以有利于中等及以下学生.

4 高考踩分技巧研究

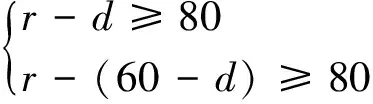
(3)过程中可保留数值的其他形式，最终结果为最简并作答如AC长度的其他形式但最终结果150必须最简.

5 教学建议

(1)书写工整，字迹清楚，不涂改.改卷过程中改卷老师在一堆字迹中寻找前面给的采分点，但往往一些字迹潦草不易发现如果几秒内无法发现分差可能就有10分以上差距甚至在三批后也有误批现象.研究生阅卷时，为了抢题甚至给个中值分就有2分差异.

(2)教学过程中强调正解不是解法越多越好，最多三种解法.其他解法应慎讲慎用.如本题已知定点A、C和B方向正解是建系利用解析几何求出B点坐标，教学时在三角和向量中能建系的尽量建系可以避开平面几何的复杂，本题中很多学生做了辅助线绕来绕去绕不出来.

(3)解题教学中注重过程中的列式，列式最好保留初始值带入，不能直接以最简形式出现容易错，若列式正确即使化简错误也可得分.计算时写出主要步骤如：tan∠BCO的拆角公式不能直接得到tan∠ACB，否则即使结果正确也扣2分.

(4)解题过程如错误不要划线，一影响美观，二可能正确，改卷过程中很多学生求对了可惜被划掉而与好几分失之交臂.

(5)应用题最重结果，以最简数值呈现作答时回到题意带单位.