几种常用似大地水准面插值方法精度分析

徐 平 ,杜向锋

(1．广东省核工业地质局测绘院，广东 广州 510800;2.广东工贸职业技术学院,广东 广州 510510)

0 引 言

GPS定位具有：测量精度高，测站间无需通视，观测时间短，仪器操作简便，全天候作业等特点，它能够提供从毫米级到几十米量级的定位精度，能够满足不同用户对定位精度的要求，GPS测量获得的高精度的三维坐标(B大地维度、L大地精度和H大地高)属于WGS84坐标系，其坐标可以通过坐标转换或平差的方法得出其1980年西安坐标系或地方坐标系平面坐标，精度可达到10-6～10-9量级[1]，可直接应用于各类工程建设，高程方面我国采用的是正常高系统，故GPS测量获得大地高需要转换成正常高才能应用于生产实践。一般说来GPS高程转换的方法有以下四类：模型拟合法、坐标转换法、神经网络法和借助区域似大地水准面模型法[2]。

目前国内多个城市、省域以及地区都已经建立或者正在建立本区域的高精度的似大地水准面模型[3-6]，与此同时高精度、高分辨率、完全覆盖我国国土的新一代中国似大地水准面CQG2000已经建设完成[7]，利用高精度的似大地水准面模型通过内插算法即可以快速的获得待定点的正常高，以此可以替代效率低下的水准测量，大大提高生产效率，降低企业生产成本，要利用GPS技术及似大地水准面模型快速的获得高精度的正常高主要取决于以下三个方面：1)待转换点WGS-84坐标的精度，特别是大地高的精度;2)似大地水准面模型本身的精度;3)内插方法的优劣。第一个方面可以根据需要采用高精度GPS测量设备、在有利的观测条件下对待转换点进行长时间多测回的观测以保证获得的待定点高精度的点位坐标，第二点取决于采用高程异常内插模型即似大地水准面模型的精度，关于如何获得高精度的似大地水准面模型本文将不再介绍了，在待定点坐标以及区域似大地水准面确定的情况下，选择一种合适的内插算法将有利于用户获得高精度的正常高结果，因此本文将着重探讨各种常见似大地水准面模型的内插方法及其精度。

1 常用插值方法的数学模型

目前用于似大地水准面内插高程异常的算法很多，主要包括：反距离加权插值、谢别德插值、线性多项式插值、三角函数插值、切比雪夫插值以及样条曲面插值等[8]。对几种常见内插方法的数学模型进行介绍

1.1 反距离加权插值

距离反比插值法是利用插值点与似大地水准面格网点之间的距离为权重进行加权计算的插值方法,离插值点越近的格网点赋予的权重越大,其权重贡献与距离成反比.可表示为

(1)

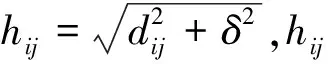
1.2 谢别德插值

与反距离加权插值类似,谢别德插值也是一种加权计算法,其权函数P(ri)定义为

(2)

式中:ri为插值点与格网点之间的距离;R为选取的内插半径。其对应的高程异常插值函数为

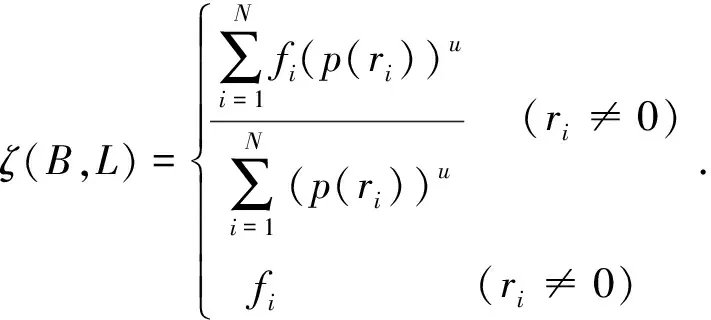
(3)

1.3 线性多项式插值

线性多项式内插的基本思想是假设任意点的高程异常与其位置是成线性关系的。

高程异常的表达式可表示为

ζ=a0+a1B+a2L+a3BL,

(4)

式中:ζ为任意点高程异常值;B和L为该点经纬度,亦可用X和Y代替；a0、a1、a2和a3为多项式系数,若a3=0则称为线性内插,a3≠0时为双线性内插,双线性内插方法的优点是数据重采样后的结果较为平滑,没有阶跃效应,同时具有较高的精度.缺点是网格被平均化,具有低频滤波的效果; 边缘被平滑,有些极值丢失了[10].

1.4 切比雪夫插值

二维切比雪夫多项式形式为[11]

(5)

式中:n,m为截止阶数,Ui(τi)和Uj(τj)为第二类切比雪夫多项式,形式为

(6)

式中,对于|τ|≤1,U0(τ)=1.0,U1(τ)=2.0τ,Un(τ)=2.0τUn-1(τ)-Un-2(τ),内插区间为[t1,t2]时需先将其转换到[-1,1]再进行内插计算。

此外常见的内插方法还包括三角函数法、样条曲面法、克里金法和径向函数法等，详见相关文献。

2 精度分析

某似大地水准面模型由地面重力数据、SRTM数字地面模型、EGM2008全球重力场模型及GPS/水准数据联合确定，其中水准测量按照国家三等水准测量精度测定，GPS网按照国家D级精度进行施测，最终获得了30″×30″(约相当于1 km×1 km)分辨率的似大地水准面模型，通过内符合精度检验和外符合精度检验的结果，该似大地水准面模型的精度优于1 cm精度水平，似大地水准面模型如图1所示，根据应用需要及相关内插方法的数学模型编制了相应的内插软件QGEOID供用户使用，软件如图2所示。

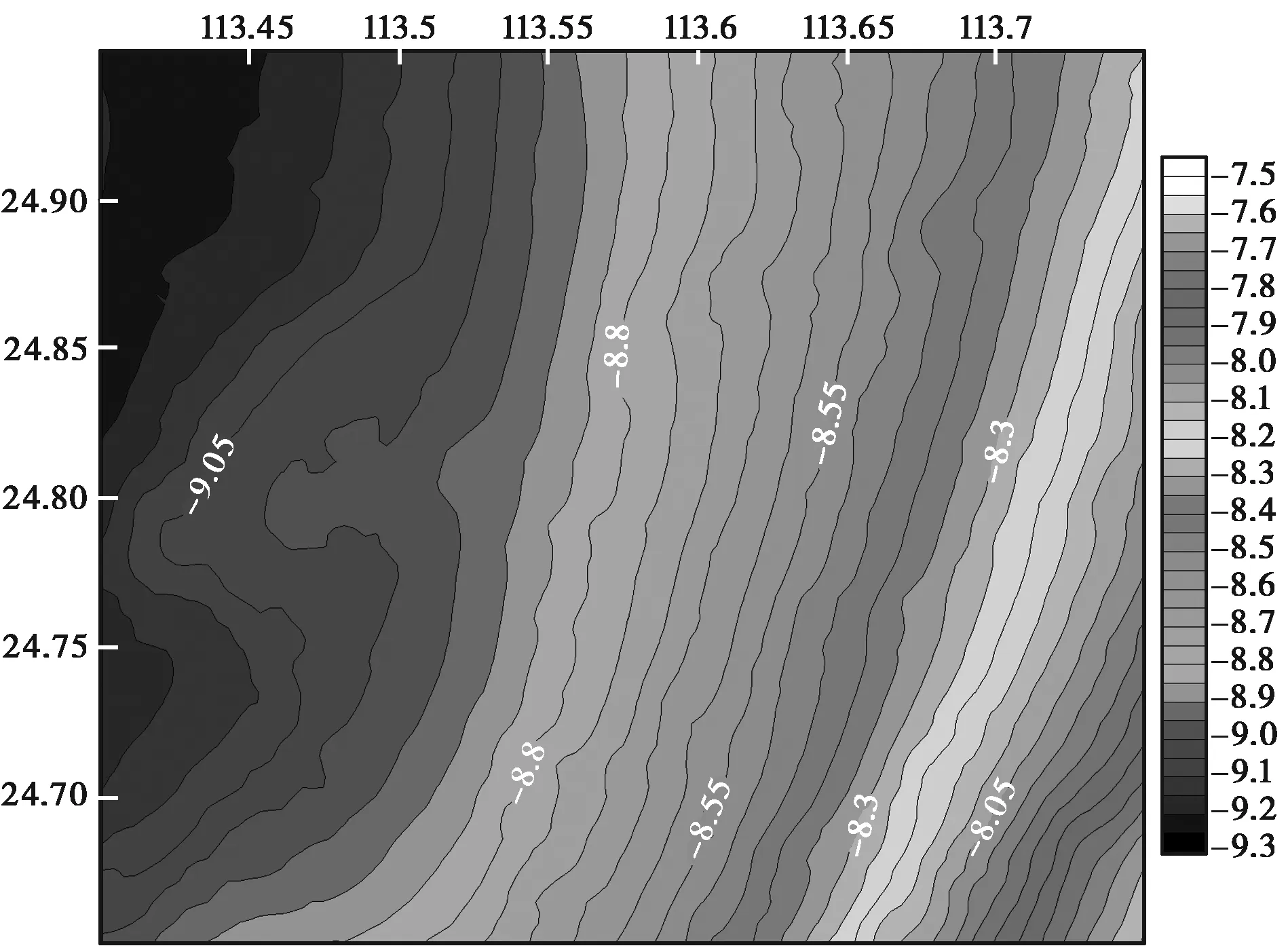
图1 某似大地水准面模型

图2 QGEOID用户界面

为了验证各种内插方法精度，探求哪种内插方法更适用于似大地水准面模型内插，采用5个GPS/水准数据利用QGEOID软件及该似大地水准面模型行了插值计算，将不同内插算法计算的结果与水准结果进行了对比，计算结果如表1所示。

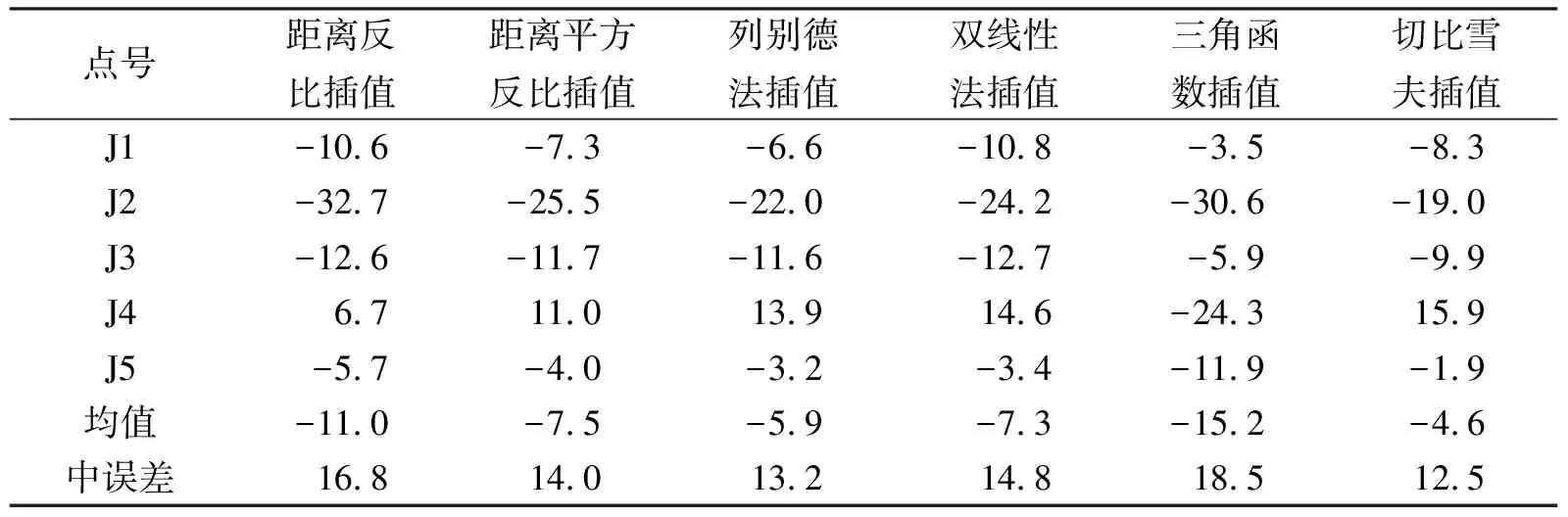
表1 不同内插方法计算结果对比(单位mm)

从计算的结果来看，J2点的转换精度无论采用哪种方法都较差，这主要是因待转换点的精度不高造成的，在待转换点坐标和似大地水准面模型确定的情况下，同一点不同方法转换出来的精度差异也较为明显，这就是内插方法不同造成的，通过对计算结果的分析，可以看出，切比雪夫内插的精度最高为12.5 mm，列别德法内插的精度次之13.2 mm，三角函数插值的精度的精度最弱达18.5 mm，距离反比插值次之为16.8 mm，此外距离反比插值和距离平方反比插值结果相比，可以看出距离平方反比插值的方法精度精度得到大幅度提升，这与文献[7]的研究成果是吻合的。

3 结束语

通过对以上数据的分析计算，可以得到如下几点结论：1)要获得比较好的转换结果，首先应保证外业测量的精度，其次才是选择内插方法。2)利用常见的几种不同内插方法的获得的计算结果差异还是比较明显，因此在作业时需要选择适当的内插方法及计算参数进行内插计算。3)切比雪夫插值和列别德插值两种内插方法在一般的似大地水准面内插计算中精度是比较高的，在水准面模型的边沿慎用距离反比插值。4)建议在确定似大地水准面模型进行外符合精度检验时利用检验数据对似大地水准面模型进行大量多模型的分析计算，寻找最适合特定模型的内插方法和计算参数作为内插该模型的推荐方法，以提高内插该模型时获得的正常高精度。

[1]鄂栋臣，詹必伟，姜卫平，等．应用GAMIT/GLOBK软件进行高精度的GPS数据处理[J]．极地研究，2005，17(3)：173-182．

[2]张兴福，于红波.模型拟合法进行GPS高程转换的研究及软件开发[J].广东工业大学学报，2008，25(3)：61-65.

[3]杨 光,林 鸿,欧海平,等.广州市亚厘米级高精度似大地水准面的确定[J].测绘通报，2007，01：24-25，32.

[4]宋玉兵,朱风云.江苏省域似大地水准面成果的应用分析[J].测绘通报,2003,12:6-8.

[5]宁津生,罗志才,杨沾吉,等.深圳市1 km高分辨率厘米级高精度大地水准面的确定[J].测绘学报，2003(2):102-107.

[6]陈俊勇,李建成,宁津生,等.全国及部分省市地区高精度高分辨率似大地水准面的研究和实施[J].测绘通报,2005(5):1-5.

[7]李建成,陈俊勇,宁津生，等.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉大学出版社,2003：6-9.

[8]朱会义,刘述林,贾绍凤.自然地理要素空间插值的几个问题[J].地理研究,2004,23(4)：425-432.

[9]HUSAR R B,FALKE S R,Uncertainty in the spatial interpolation of PM10 monitoring data in Southern California[EB/OL].[2007-09-27].http://capita.wustl.edu/capita/capitareports/cainterp/cainterp.html.

[10]李 新,程国栋,卢 玲.空间内插方法比较[J].地球科学进展,2000,15(3):260-265.

[11]张兴福,魏德宏.基于似大地水准面格网的插值方法及精度分析[J].大地测量与地球动力学,2011,31(1):113-116，122.