基于两步最小均方的宽带波束形成算法

郑永翔,任 超,窦亚军

(北京北斗星通导航技术股份有限公司,北京 100081)

0 引 言

波束形成是卫星导航、雷达和通信信号处理中的一个重要组成部分[1]。波束形成系统可以看作是一种应用在空间域的滤波器,它使得天线阵只在某一方向具有较高的增益,而在其它方向具有较低的增益,甚至可以在某一方向产生很深的零陷,抑制来自该方向的的干扰。要实现快速、准确的方向图合成,这主要取决于所使用的波束形成算法。例如,在文献[2]和[3]中描述了将RLS和LMS分别进行级联,可以得到两个快速有效的波束形成算法RLMS和LLMS。文献[4]中采用了一种基于切比雪夫多项式的改进波束形成算法,可以大大降低计算的复杂度。

在文献[5]～[7]的基础上,采用空时二维滤波器结构,提出了修正两步最小均方波束形成算法。本算法修正了每次迭代运算中的期望响应幅度和方向矩阵,可以显著地减少矩阵运算量,快速准确地求解出期望方向图的相位和相应的权矢量。此外,本算法在不改变天线阵元数的情况下,增加了时域处理维数,达到改善波束形成质量的目的。可广泛应用于多天线的GNSS导航接收机或抗干扰接收机中,在提高接收机在复杂环境下的可用性和灵敏度上具有重要的意义。

1 问题提出

空时自适应滤波是将一维的空域滤波推广到时间与空间的二维域中,形成空时二维滤波器结构,其实现结构如图1所示。

图1 空时二维滤波器结构图

图中M为空时二维滤波器的天线阵元个数;N为每 个阵元通道后FIR滤波器阶数。{xmn}(m=1,2,…,M，n=1,2,…,N)为M路天线阵元接收到的输入信号在FIR滤波器中延迟了n-1个处理节拍后的信号。{wmn}(m=1,2,…,M，n=1,2,…,N)为M个FIR滤波器的系数,即空时二维权系数。y为各路FIR滤波器的合路输出,即空时二维滤波器的输出。每个处理节拍延时为 (T<1/B,B为信号带宽),则每个阵元后信号总的延时长度(N-1)T,要求能够包括不同的多径延时。空时滤波器权可用MN×1维向量表示为

W=[w11,w12,…,w1N,w21,…,w2N,…,

wM1,…,wMN]T.

(1)

各阵元接收数据组成的协方差矩阵

R=E[XXH].

(2)

空时二维导向矢量a可写成

a=Ss⊗St,

(3)

式中:矢量Ss=[1,ejωs,…,ej(M-1)ωs]T为空间导向矢量;ωs为空间归一化频率;St=[1,ejωt,…,ej(N-1)ωt]T为时间导向矢量;ωt为时间归一化频率,⊗表示可罗奈克积。

假设有Ns个窄带平面波信号si,i=1,2,…Ns入射到空间中M元均匀线阵上,阵元间距为接收到信号中最高频率所对应的波长的一半。假设有用信号的带宽为B,则第m个阵元的接收到的数据为

m=1,2,…,M,

(4)

式中,nm(t)为第m个阵元通道的热噪声。对其中某一个通道的数据进行K点的离散傅立叶变换,可以得到如下的宽带模型

X(fk)=A(fk)S(fk)+N(fk),

k=1,2,…,K.

(5)

式中:X(fk)为对应频率fk的接收数据;S(fk)为信号的离散傅立叶变换;N(fk)噪声的离散傅立叶变换;A(fk)=[a1(θ1,fk)a2(θ2,fk)…aNs(θNs,fk)]为信号导向矢量矩阵。

空频二维方向图的阵列响应可表示为

P(θ,f)=WHA(θ,f),θ∈Θf∈B,

(6)

式中:Θ∈[-90°,90°]为信号波达角的集合;B为接收信号带宽。

2 基于空时结构最小均方的方向图控制

阵列方向图合成问题就是使合成方向图与期望方向图的误差最小化,因此可表示为

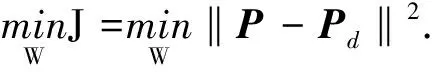
(7)

考虑下面的公式

Pd(θ,f)=WHV(θ,f),θ∈Θf∈B.

(8)

其中矢量

Pd=[Pd(θ1,f),…,Pd(θN,f)]

(θ1,…,θN∈Θ,f∈B),

来自进博会的数据显示, 3000多家参展企业中,不仅涉及G20全部成员,覆盖超过50个“一带一路”沿线国家和地区,全球44个最不发达国家中,也有超过30个前来参加。大量外国参展商希望抓住中国消费升级和高质量发展的机遇,借助进博会的平台,在中国市场“更进一步”。

为期望阵列响应。而方向图合成就是要寻找最优的W,使等式(7)中的J值最小。在大多数应用中,选择的角度θ与频率f的个数N远大于阵元数M,所以使用最小均方算法来求解等式(7)。

显然,期望阵列响应Pd(θ,f)可表示为

Pd(θ,f)=PdM(θ,f)PdP(θ,f),θ∈Θf∈B.

(9)

式中,PdP(θ,f)=exp(j∠Pd(θ,f)),θ∈Θ，f∈B;PdM(θ,f)=|Pd(θ,f)|.

所以

Pd=PdMPdP=PdP·diag(PdM),

(10)

式中:PdM=[PdM(θ1,f),…,PdM(θN,f)];PdP=[PdP(θ1,f),…,PdP(θN,f)] (θ1,…,θN∈Θf∈B).

方向图合成问题可以表示为

diag(PdM)‖2.

(11)

基于等式 (11)的方向图合成算法步骤概括如下:

第1步:初始化期望阵列响应幅度PM=|W0HVpattern|,其中W0为最优权矢量的初值Vpattern:[V(γ1,η1),…,V(γK,ηN)](γ1,…,γK∈Θ,η1,…,ηK∈B)为方向矩阵的初值;Θ∈[-90°,90°]为期望方向图中增益峰值所对应的波达角的集合,B为接收信号带宽,设迭代次数n=0.

第3步:用找到的θi和fi更新迭代算法中的PdM和V

PdM=[Pml,PdM(θ1,f1),…,PdM(θL,fK)],

(12)

V=[Vml,V(θ1,f1),…,V(θL,fK)],

(13)

式中:Pml和Vml分别为天线阵主瓣所指方向对应的阵列响应幅度和方向导向矢量。

第4步:采用文献[7]中两步最小均方算法更新权矢量Wn,迭代次数n=n+1.

(14)

Pdp0=Pdp/|Pdp|,

(15)

(16)

第5步:重复第2～4步,直到‖Wn-Wn-1‖2小于允许的方向图合成误差ε.

对于上述算法,有以下几点说明:

1)依据期望方向图的增益,可将波达角与频率组成的二维集合(Θ,B)分为主瓣区域和旁瓣区域,由此可确定主瓣区域对应的阵列响应幅度Pml和方向导向矢量Vml.在第一步初始化方向矩阵Vpattern时,选择扫描角度与频率的间隔越大,计算量越小;间隔越小,方向图越平滑。在后面的仿真实验中,扫描角度间隔选为0.1°,扫描频率间隔选为1 MHz.

2)在第1步中,权矢量的初值W0可设为Capon波束形成算法的解[8]

W=R-1a(θ0,f)/(aH(θ0,f)R-1a(θ0,f)),

式中:(θ0,f)是天线主瓣指向方向;R=V(θ0,f)VH(θ0,f)+σ2I;σ为一个非常小的实数,I为单位矩阵。

3)在第3步中,在迭代时通常只关心主瓣的响应,不去约束旁瓣并不会对方向图合成结果造成明显的影响,但是却可以大大减少矩阵运算量。

4)通常情况下,第4步中方向图合成的允许误差选为ε=10-4.

3 计算机仿真

通过两个计算机仿真实验来验证本文提出的阵列方向图合成算法可以合成任意的波束,以适应不同场景的需要。

实验一:考虑7元均匀线阵结构,阵元间距d=λ/2,λ为接收信号载波频率对应的波长。确定主瓣区域为[-30°,0°],对应的阵列响应幅度为0 dB; 其余角度空间为旁瓣区域,对应的阵列响应幅度为-40 dB.每个阵元通道的FIR滤波器阶数为5.计算机仿真有用信号叠加宽带扩频干扰信号,有用信号为带宽20 MHz的BPSK调制信号,信号中心频率为15.48 MHz,干扰信号为带宽20 MHz的BPSK调制信号,与信号同频,采样率62 MHz.若选择允许误差ε=10-4,自适应方向图控制算法通过10次迭代运算可以收敛,收敛结果,如图2所示。从图中可以看出,主瓣和旁瓣在各个频点的阵列响应幅度都很好的收敛到期望的响应,这样,只要保证有用信号从主瓣区域入射,而干扰信号落入旁瓣区域,即使干扰与信号同频,也可达到很好的抑制效果。

图2 7元线阵方向图收敛结果

实验二:考虑30元均匀线阵结构,采用本文算法设置阶跃式旁瓣包络,首先确定主瓣区域为[-5°,5°],对应的阵列响应幅度为0 dB;旁瓣区域[-40°,-5°]和[5°,40°],对应的阵列响应幅度为-30 dB,旁瓣区域[-90°,-40°]和[40°,90°],对应的阵列响应幅度为-40 dB.每个阵元通道的FIR滤波器阶数为5.计算机仿真有用信号叠加宽带扩频干扰信号,有用信号为带宽20 MHz的BPSK调制信号,信号中心频率为15.48 MHz,干扰信号为带宽20 MHz的BPSK调制信号,与信号同频,采样率62 MHz.选择允许误差ε=10-4,自适应方向图控制算法迭代30次收敛结果如图3所示。同样的阵列结构设置锲形旁瓣包络时,在区间[-90°,-5°]内,阵列响应幅度从-50 dB开始以0.2 dB/(°)的速度上升到达-5°,在区间[5°,90°]内,阵列响应幅度以0.2 dB/(°)的速度下降到-50 dB,形成一个锲形包络。确定主瓣区域为[-5°,5°],对应的阵列响应幅度为0 dB.选择允许误差ε=10-4,自适应方向图控制算法迭代30次收敛结果，如图4所示。同上个实验相比,此例中的主瓣区域更窄,但相应旁瓣区域的响应幅度略高,对于与信号方向相近的干扰区分度更高,具有更明显的抑制效果。

图3 30元线阵阶跃式旁瓣方向图

图4 30元线阵锲形旁瓣方向图

4 结束语

本文结合空时滤波器结构提出了一种新的基于两步最小均方的方向图合成算法。算法的核心在于通过修正迭代运算中的期望阵列响应幅度和方向矩阵,在每次迭代中只约束主瓣方向矢量,因此可以大大降低矩阵运算复杂度,并快速准确地求解出期望方向图的相位和相应的权矢量,同时利用额外的时域处理维数改善了波束合成质量。最后通过几个计算机仿真实验充分验证了该算法的有效性。

[1] MARTIN-SACRISTAN D, MONSERRAT J F, JORGE CABREJAS-PEUELAS,etal. On the way toward forth-generation mobile:3GPP LTE-advanced[J].EURASIP Journal on Wireless Communications and Networking,2009.doi:10.1155/2009/354689.

[2] BECKER J M, LOHN J D, LINDEN D. Towards a self-healing, anti-jamming adaptive beamforming array[C]//2013 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), 2013:1477-1480.

[3] SRAR J A,CHUNG Kahseng. Adaptive RLMS algorithm for antenna array beamforming[C]//TENCON 2009-2009 IEEE Region 10 Conference, Singapore, 2008.

[4] SRAR J A, CHUNG Kahseng.A new LLMS algorithm for antenna array beamforming[C]//2010 IEEE Wireless Communications and Networking Conference (WCNC), Sydney, NSW, April, 2010.

[5] JIAO Jiping, ZHOU Youling, BAI Yong, An improved array pattern synthesis algorithm based on Chebyshev polynomial[C]//2011 International Conference on Computer Science and Network Technology (ICCSNT), Harbin, China, Dec. 2011:1125-1127.

[6] WANG Fan, YANG R, FRANK C. A new algorithm for array pattern synthesis using the recursive least squares method[J], IEEE Signal Process Lett,2003(8):235-238.

[7] SHI Zhan, FENG Zhenghe, A new array pattern synthesis algorithm using the two-step least-squares method[J], IEEE Signal Process. Lett., 2005:250-253.

[8] HAYKIN S. Adaptive filter theory[M].4 ed. New Jersey:Englewood Cliffs,1991.