基于VB6.0的水准网数据处理程序的实现
2014-08-21陈帅,王鹏
陈 帅,王 鹏
(天津市普迅电力信息技术有限公司,天津 300000)
0 引 言
目前,高等级水准测量仍然是矿区进行开采沉陷观测的主要方法,而水准网的数据处理流程繁琐且量大,大多数矿区当前使用的水准网数据处理程序或软件都不同程度的存在不足,如:程序不能自动进行闭合条件的搜索和闭合差的计算,单纯依靠人工计算,费时费力;一般的平差程序是以固定基准模型设计的,不能根据矿区的实际情况及工程本身特点选择合适的平差基准模型来处理数据[1-2];不能进行抗差处理,消除观测粗差的影响等。
VB6.0是一种可视化、面向对象的开发语言[3],文章基于VB6.0的语言环境,进行了矿区水准网综合数据处理程序的编写,实现了对不同平差基准的水准网进行最小二乘估计和抗差估计,以及自动进行闭合环的搜索和闭合差的计算等功能,完善了矿区水准网数据处理流程,减少了作业人员的工作量,提高了工作效率。
1 数学模型
1.1 平差基准模型

l=L-(AX0+d),
(1)

根据最小二乘原理可知:

(2)
单位权中误差为[5]:

(3)
式中,P为观测值的权阵。


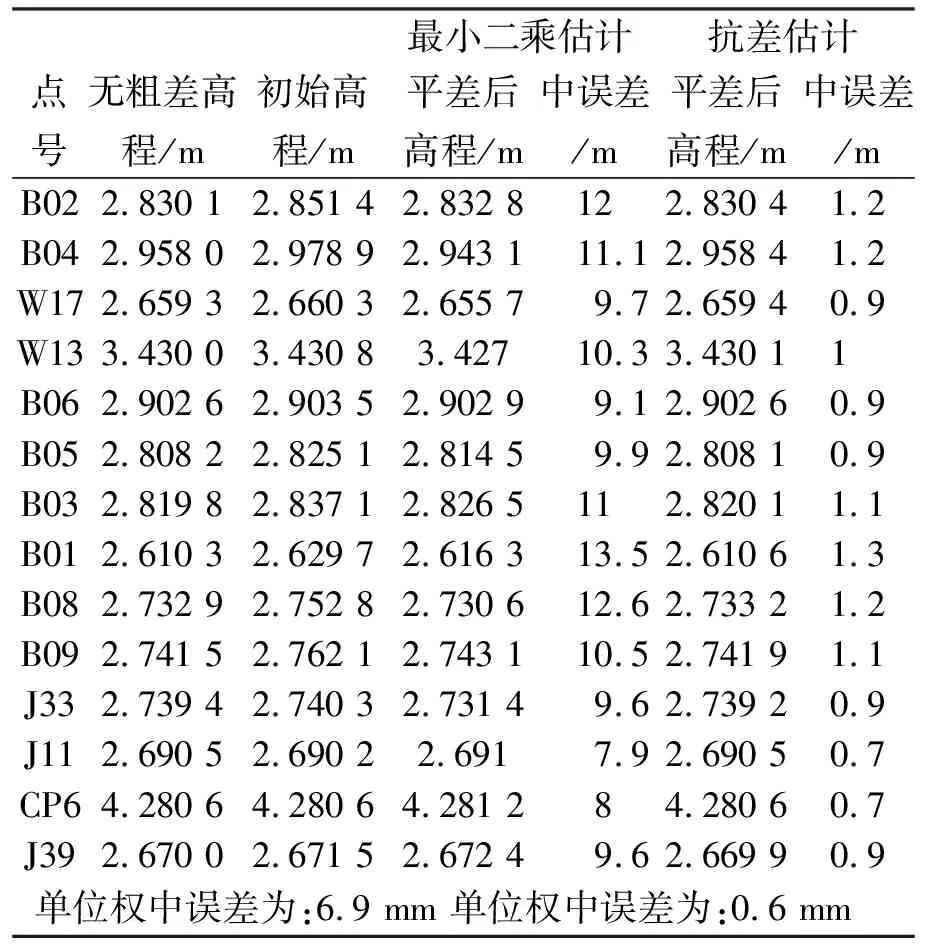
R(A)=m 给定约束条件为 由最小二乘原理[7]可知: (4) 式中, Qp=(ATPA+PxSSTPx)-1 =(N+PxSSTPx)-1. (5) 取S为 ST=(1 1 … 1). 当采用秩亏基准时 Px=E. (6) 当采用拟稳基准, (7) 式中:μ2>d,μ1+μ2=μ. (8) 式中:Wi的计算采用IGG3函数,以固定基准为例,其抗差解为 (9) 当参数两次估值之差的绝对值中的最大值小于迭代精度时,迭代停止,单位权中误差为 (10) 式中:n0为权因子,且等于0的观测值个数。 程序可实现的设计功能有:闭合差计算、近似高程计算、平差计算等,以上功能分别基于固定基准、秩亏基准及拟稳基准,将采集的水准数据按照特定格式整理好,选择基准类型,从导入模块进行导入,一次进行操作,注意在平差前需进行抗差参数设置。 外业水准测量结束后,为保证测量结果的质量,一般都要进行闭合差的计算,是否符合相应等级水准测量要求,由于环线和附合路线的闭合差计算都涉及到搜索最短路径的,因此首先进行最短路径搜索程序的设计。 限于篇幅,以下只给出最短路径搜索的关键步骤代码:建立两个数组ljd和S,分别记录每个点的邻接点号及其到目标点的路线长度;设m点为目标点点号。 For j=1 To tn ljd(j)=-1 S (j)=1E+30 Next i S(m)=0 ljd(m)=m Dim p1%, p2% p1=begin(j) p2=end(j) If S(p2)> S(p1)+S12 Then ljd(p2)=p1 S(p2)=S(p1)+S12 ElseIf S(p1)> S(p2)+S12 Then Ljd(p1)=p2 S(p1)=S(p2)+S12 将上述编码编写成过程FSP(),在进行闭合差搜索与最小独立闭合环搜索编码时调用此过程。 闭合差限差的计算公式如下: (11) 式中,sigma0为给定的先验单位权中误差。 在水准网进行平差之前需求解未知点的近似高程值,程序设计思路如下:给所有未知点的近似高程绝对值很大的负数,对网中所有观测值进行搜索,当观测值出现起点和终点一个大于该负数,一个小于该负数,说明该观测值的一端近似高程已知,另一端未知,再根据已知点高程值和高差推算出未知点的近似高程值,那么在之后的程序判别过程中该点就作为已知点来处理,以此类推,直到求解出所有未知点的近似高程时程序结束。 计算近似高程的程序代码如下: Dim Elevation()As Double '存放高程和高程近似值 Dim begin(), end()'编号数组,存储的是点的序 Dim h()' 高差观测值数组 For j=1 To su 'su为高程未知点个数 Elevation (sn+j)=-9999 'sn为高程已知点个数 Next j n=0 Do While k < su For j=1 To sh 'sh为观测高差数 If Elevation (begin(j))>-9999And Elevation (end(j))<-9999Then '起始点已知,终点未知 Elevation (end(j))= Elevation (begin (j))+h(j) n=n+1 ElseIf Elevation (end(j))>-9999 And Elevation (begin(j))<-9999 Then '起始点未知,终点已知 Elevation (begin(j))=Elevation end(j))-h(j) n=n+1 End If Next j Loop 程序运行时应生成误差方程的B阵、P阵和l阵,P阵和l阵的形成相对较为简单,限于篇幅,下面给出B阵形成的代码。对于固定基准,代码如下: For j = 1 To sh If begin(j)> sn Then b(j, begin (j)- sn)= -1 End If If end(j)> sn Then b(j, end(j)- sn)= 1 End If Next i 抗差估迭代计算过程对两次求解的参数进行比较,当它们的之差的绝对值的最大值小于迭代条件的时候,迭代停止。下面给出固定基准中迭代实现的代码: nn=1 Do While nn > eps For i = 1 To su b(j)= a(j, 1) Next j Call Ca_UintV(sh, sdd, d, dv, M)'利用中位数计算单位权方差因子M以及标准化残差数组dv的计算 For j = 1 To sh W(j)= Wj("IGG3", dv(j), n0, n1)'权因子计算函数 p(j, ij)= p1(j, j)* W(i) Next j Call zxec(e, r, s, d, l, q, PVV)'最小二乘求解过程 For j = 1 To su b(j)= Abs(a(j, 1)- b(j)) Next j nn = max(b)'max为编写的最大值求解函数 Loop 采用某地实测闭合水准路线数据进行程序验证,网中共有25个高差观测值,B0为已知高程点,具体数据如表1所示。 表1 观测数据和已知点高程 现用以上数据导入程序,以固定基准为例进行如下操作: 1)闭合条件搜索和闭合差计算 环闭合差:B02-B03-B05-B04-B02,W=0.000 1(限差:0.006 2). 环闭合差:B04-B05-B06-W17-B04,W=0.001 1(限差:0.005 4). 环闭合差:W17-B06-J11-B0-W13-W17,W=0.001 1(限差:0.006 4). 环闭合差:B02-B03-B01-B02,W=0.004 5(限差:0.006 2). 环闭合差:B03-B09-B08-B03,W=-0.000 6(限差:0.005 3). 环闭合差:B05-B03-B09-J33-B05, W=0.000 8(限差:0.004 9). 环闭合差:B0-J11-J39-CP6-B0,W=-0.002 1(限差:0.006 9). 环闭合差:J33-B05-B06-J11-J33,W=0.001 1(限差:0.005 4). 环闭合差:J39-B09-J33-J39,W=0.001 1(限差:0.004 3). 环闭合差:B08-B03-B01-B08,W=0.002 6(限差:0.005 9). 路线闭合差计算:无附合路线。 2)固定基准的最小二乘估计 对表1中的数据作固定基准最小二乘估计,求得的高程平差值与高程中误差如表2所示。 表2 固定基准最小二乘估计 3)秩亏基准的最小二乘估计 对表1中的数据作秩亏基准最小二乘估计,求得的高程平差值与高程中误差如表3所示。 表3 秩亏基准最小二乘估计 由表2和表3可以看出,由固定基准和秩亏基准的最小二乘结算的高程平差值基本一致。 4)在B05-B04观测高差中加入-0.04 m模拟粗差,J33-B09观测高差中加入+0.02 m模拟粗差,对含粗差的数据分别进行最小二乘估计和抗差估计,将结果对比,如表4所示。 表4 最小二乘估计与抗差估计对比表 通过表4可以看出,在数据中加入粗差后进行最小二乘估计,其单位权中误差显著增大,为6.9 mm,高程平差值与表2中高程平差值相差较大。而同样的数据进行抗差估计的结果与表2中高程平差值基本一致,从而验证了抗差估计程序的准确性与可靠性。 基于VB6.0语言环境设计了矿区水准网综合数据处理的程序,实现了对三种不同平差基准的水准网数据进行最小二乘估计和抗差估计,同时实现了程序自动进行闭合环的搜索和闭合差的计算等功能,并对程序实现中的关键性问题进行了比较详细的分析并给出了部分程序实现的代码。通过实际算例,分析验证了程序的可靠性与准确性,同时也弥补了现有矿区水准网平差程序或软件中存在的不足,减少了作业人员的工作量,提高了工作效率。 [1] 付江缺,高万柱,张袭远,等.水准网自动处理模型及程序实现[J].测绘工程,2013,22(5):69-70. [2] 刘忠林,薛维刚.精密跨河水准测量方法与数据处理[J].测绘空间与地理信息,2009,32(4):204-206. [3] 潘地林.Visual Basic 程序设计[M].北京:高等教育出版社,2006. [4] 黄维彬.近代平差理论及其应用[M].北京:解放军出版社,1992. [5] 李 巍,赵 亮,张占伟,等.基于VC的水准网平差程序的设计与研究[J].测绘通报,2013,(5):20-22. [6] 查 明,段五杏,徐必林,等.全国GPS二级网数据处理和精度分析[J].全球定位系统,2001,26(1):14-18. [7] 崔希璋,於宗俦,陶本藻,等.广义测量平差[M].2版.武汉:武汉大学出版社,2009.

1.2 抗差模型



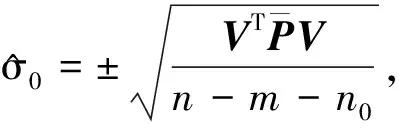
2 程序设计
2.1 功能设计
2.2 搜索闭合条件并计算闭合差
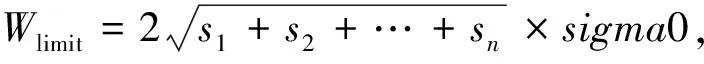
2.3 求解未知点的近似高程
2.4 误差方程的形成
2.5 抗差迭代计算
3 算例分析



4 结束语
