分形理论在岩体稳定性分析中的应用

(上海市政工程设计研究总院(集团)有限公司，上海 200433)

1 研究背景

长期以来，自然科学工作者由于受到欧几里德几何学以及传统数学方法的影响，习惯将复杂的研究对象进行简化与抽象，建立起各种理想模型(绝大多数为线性模型)，从而将问题纳入到可以解决的范畴。这种近似线性的处理方法虽然对有些问题很有效，但是难以认识到与非线性有关的特性。物质世界绝大部分不是规整有序、稳定和平衡的，是非线性的[1]。分形理论是在20世纪70年代末80年代初出现的处理复杂性问题的数学理论。一般把在形态、结构、功能和信息等方面具有自相似性或者统计自相似性的研究对象统称为分形，而分形的定量表征就是分维，分形和分维与其他数学概念一样，都是从客观存在的数形关系中抽象出来的[2]。

分形理论是处理自然界中那些极不规则构型的有力工具，目前已在岩土力学中得到了成功应用，如土的微结构分析、岩石节理表面分形、节理分布分形、岩体损伤特征等方面[3-4]；但对于分形理论在岩体稳定性分析中的应用研究较少且不系统。本文结合工程实例，依托Matlab强大的数值计算能力，自编程序，通过岩体变形过程中的分维特征验证岩体变形分维预报的合理性与有效性，并总结相关规律，以供实际岩土工程设计、施工与运营参考。

2 分维的计算方法

目前对岩体复杂系统量化信息的探测，最常见的就是位移动态监测[5]。因此可以采用位移时间序列来重建岩体变形破坏的分维动态特征[6-7]。

一般来说，通常认为单变量位移时间序列只能提供岩体系统十分有限的信息，甚至有人可能认为可以用“一维”的观点处理实际上含有大量相互关联的复杂体系。实际上位移时间序列本身包含着比人们想象更为丰富的信息，它是岩体变形或者失效的综合反映，蕴含着参与变形动态过程全部变量的痕迹。因此利用位移时间序列重建岩体系统变形破坏的动态分维过程，可为岩体稳定性分析提供可靠的依据，为失稳预报提供重要的信息。

以X(t)为监测所获取的位移时间序列，选择一个固定的时间间隔Δt，将原有序列X(t)加以拓展，并从数据集中取m个等距节点，得到新的变量组：

X1:X(t1),X(t2),X(t3),…,X(tm);

X2:X(t1+Δt),X(t2+Δt),X(t3+Δt),…,

X(tm+Δt);

X3:X(t1+2Δt),X(t2+2Δt),X(t3+2Δt),…,

X(tm+2Δt);

Xn:X(t1+(n-1)Δt),X(t2+(n-1)Δt),

X(t3+(n-1)Δt),…,X(tm+(n-1)Δt)。

{X(ti),X(ti+Δt),…,X(ti+(n-1)Δt)} ，

(1)

式中θ(x)为Heaviside函数，它的定义为

(2)

可以证明，当r较小时，C(r)=rD。若在一定范围内取不同r值，则lnC(r)与lnr之间呈现线性关系。因此可以用lnr和lnC(r)作坐标图，找出无标度区的斜率D(见图1)：

(3)

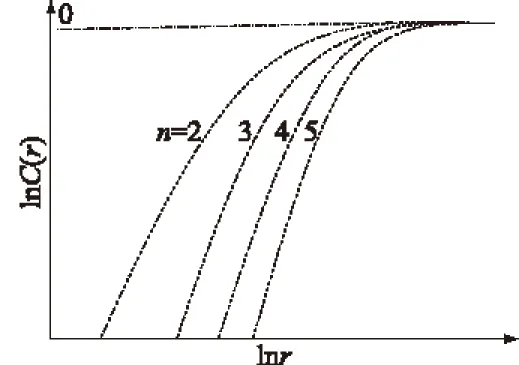
图1 lnC(r)-lnr曲线

然后考察D随相空间维数n的变化。如果随着n的增大，D值稳定，即lnC(r)-lnr曲线图出现相互平行的直线段，则称时间序列描叙的岩体系统具有吸引子，且其分维为D的稳定值。

实际计算时，通过累加生成变换能够消除或者削弱监测数据随机干扰的成分，加强其代表研究对象本质特征的确定性信息。因此在动态分维计算前，还需要对位移序列一次累加生成处理[8]。此外，如果监测所得数据偏少，还要对其进行插值处理。

3 实例分析

3.1 边坡变形过程中的分维特征

1986年长江西陵峡新滩镇发生一次大规模边坡失稳，总方量达到3×107m3，造成了极大的损失。下面取新滩边坡失稳A3点的监测信息进行分析[7]，表1为A3测点不同时期位移观测数值，图2为A3测点实测位移和位移累加值时程曲线。

表1 A3测点位移观测资料

图2 A3点实测位移曲线和位移累加值曲线

依据不同时期无标度区的形态，动态分维计算结果如图3所示，利用线性回归分析计算无标度区直线斜率即分维大小绘成图4，由此可以得出结论：

图3 边坡不同时期lnC(r)-lnr曲线

图4 边坡动态分维变化曲线

(1) 变形边坡具有分形特征，而且这种分形性质随着变形的发展越来越明显。具体体现在lnC(r)-lnr关系曲线上，无标度区和D值的稳定性在边坡变形前期不太突出，随着变形的发展，无标度区越来越明显，D值的稳定性也越来越好。

(2) 与边坡变形一样，边坡变形的动态分维具有明显的时效性，随着时间的推移，分维数D也会相应地发生变化。

(3) 边坡变形是一个升维过程，变形开始加速时分维值增大至逼近1附近，并最终导致边坡破坏。

3.2 深基坑变形过程中的分维特征

上海外滩观光隧道浦西竖井深基坑处于市区密集路网间的地块内，周边环境复杂，施工场地狭窄，基坑工程的变形保护等级为一级。该深基坑平面呈组合矩形，主体尺寸86 m×16 m，开挖深度20.43 m，端头井部分落深24.46 m。采用1 m厚地下连续墙作为围护结构，基坑内设多道支撑：第1，3，5道为O|609 mm钢支撑，第2，4，6道为C40早强混凝土支撑，第7，8道为双拼O| 609 mm钢支撑，地墙顶部设C30冠梁。沿基坑四周布设了9处地墙水平位移监测点，选取从1997-12-21至1998-02-06监测深度为34 m的地下连续墙水平位移的48个监测数据(表2及图5)进行分析[9]。

表2 地下连续墙水平位移监测数据

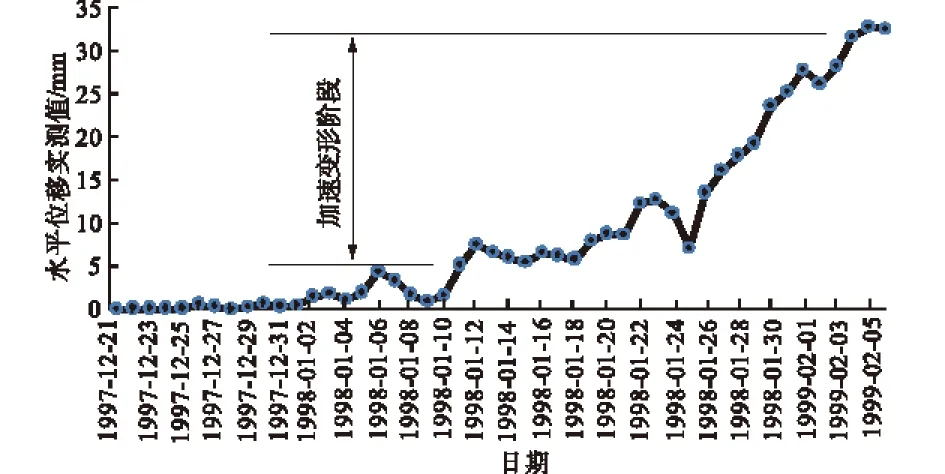
图5 地下连续墙水平位移时程曲线

动态分维计算结果如图6所示。分维值计算后，通过分析图6至图8可知：

图6 基坑不同时期lnC(r)-lnr曲线

图7 1998-02-06的分维特点

图8 基坑动态分维变化曲线

(1) 1998-01-11之前基坑水平变形较小分维不明显，随着变形的快速发展，分形越来越明显，无标度区越来越明显，D值越来越稳定。

(2) 基坑变形是一个升维过程，1998-01-22以后分维值大小基本不变，表明将保持1998-01-11至01-22之间较快的变形趋势和速率，应该引起高度重视。

3.3 隧道洞周收敛过程中的分维特征

取鹰嘴岩隧道右洞进口段的37号断面(桩号YK40+275)洞周收敛监测数据进行分析[10]，表3为实测收敛数据，图9为收敛变形监测曲线。

表3 洞室收敛数据

图9 收敛变形监测曲线

由计算结果(图10)可知，2007-10-17之后的分维基本保持不变且无标度区不明显，变形将不会继续发展 ，洞周逐渐趋于稳定，这与监测结果是相符的。

图10 隧洞不同时期的lnC(r)-lnr曲线

4 结 语

本文结合边坡工程、基坑工程和隧道工程，将分形理论系统地用于分析岩体的变形的稳定性，研究结果表明岩体位移时间序列的分维值将随着变形的发展逐渐增加，无标度区将越来越明显，利用分维的动态特征可以分析岩体对象的安全性，同时也证明了位移时序的分维值作为岩土工程安全性预警指标是合理的。

实际上目前已有大量的方法基于变形监测时间序列，用于分析岩体稳定，诸如灰色理论(Grey Theory)、神经网络(Neural network)、Verhulst函数与反Verhulst函数模型、时间序列分析模型(Time series analysis)等，这些方法均是通过变形序列本身，依托数据挖掘技术(Data mining)对将来的变形大小和规模进行预测，而分形理论则是重在研究序列本身的分维特征，不是直接进行变形预报，这与以上这些方法具有不同之处。无论怎样，这些方法都是重在趋势预测，过分追求具体数值意义不大。但是分形理论还存在许多弱点，如表征信息少、逆向分析困难等，有待进一步研究。

参考文献：

[1] 高安秀树. 分维数[M]. 沈步明，常子文，译. 北京：地震出版社，1994：1-20. (TAKAYASU H. Fractal Dimension[M]. Translated by SHEN Bu-ming，CHANG Zi-wen. Beijing：Seismological Press，1994:1-20. (in Chinese))

[2] 董连科. 分形理论及其应用[M]. 沈阳：辽宁科学技术出版社，1991：2-4. (DONG Lian-ke. Fractal Theory and Its Application[M]. Shenyang：Liaoning Science and Technology Press，1991：2-4. (in Chinese))

[3] 许宏发，陈力新. 岩石时效特性与节理模型[M]. 上海：上海交通大学出版社，2009：2-5.(XU Hong-fa，CHEN Li-xin. Rock Aging Characteristics and Joint Model[M]. Shanghai：Shanghai Jiaotong University Press，2009：2-5. (in Chinese))

[4] 谢和平. 分形-岩石力学导论[M]. 北京：科学出版社，2005：3-4.(XIE He-ping. Introduction of Fractal Rock Mechanics[M]. Beijing：Science Press，2005：3-4. (in Chinese))

[5] 夏才初，潘国荣. 土木工程监测技术[M]. 北京：中国建筑工业出版社，2001：2-5. (XIA Cai-chu，PAN Guo-rong. Monitoring Technology in Civil Engineering[M]. Beijing：China Architecture and Building Press，2001：2-5. (in Chinese))

[6] 吴中如，潘为平. 分形几何在岩土边坡稳定性分析中的应用[J]. 水利学报，1996，(4)：79-82. (WU Zhong-ru，PAN Wei-ping. Application of Fractal Geometry Theory in Stability Analysis of Rock and Soil Slope[J]. Journal of Hydraulic Engineering，1996，(4)：79-82.(in Chinese))

[7] 李天斌，王兰生. 岩质工程高边坡稳定性及其控制[M]. 北京：科学出版社，2008：169-170.(LI Tian-bin，WANG Lan-sheng. High Rock Slope Stability and Its Control[M]. Beijing：Science Press，2008：169-170. (in Chinese))

[8] 邓聚龙. 灰色预测与决策[M]. 武汉：华中理工大学出版社，1986：53-55.(DENG Ju-long. Grey Forecast and Decision Making[M]. Wuhan：Huazhong University of Science and Technology Press，1986：53-55. (in Chinese))

[9] 罗 波，远 祯. 改进BP网络在深基坑变形预测中的应用[J]. 工业建筑，2006，36(增)：683-687. (LUO bo，YUAN Zhen. Application of Improved BP Network in Deep Foundation Deformation Prediction[J]. Industrial Construction，2006，36(Sup.)：683-687. (in Chinese))

[10] 夏 冲. 公路隧道围岩位移反分析及其稳定性研究[D]. 武汉：武汉大学，2008.(XIA Chong. Back Analysis and Stability of Tunnel Surrounding Rock’s Displacement[D]. Wuhan：Wuhan University，2008. (in Chinese))