基于分析分解模型数值试验的围岩力学参数估算

(西安科技大学 建筑与土木工程学院，西安 710054)

1 研究背景

围岩力学参数是地下岩体工程进行设计与施工的基础，对工程安全性和经济性具有重要影响[1]。目前，确定围岩力学参数的常用方法有：直接法和间接法。其中直接法在室内或现场进行力学试验，依据试验实测曲线读出或拟合得到岩体力学参数，但该方法受制于岩体结构面存在，实际测试结果与真实情况往往存在一定差距，且试验成本较高，这使得间接法在一定条件下得到广泛应用。间接法包括经验统计法、经验准则推算法、反分析法及数值试验方法。随着计算机技术、计算方法、数值分析理论的发展，综合现场地质调查、结构面统计，模拟岩体节理裂隙、研究不同尺度的“岩体试件”力学行为的数值试验方法得到迅速发展，并越来越得到广泛认可与应用。

目前，数值试验方法包括连续介质数值试验和离散元数值试验。连续介质数值试验研究方面，周维垣和杨延毅[2]较早提出一种确定节理岩体力学参数的计算机模拟试验法。基于节理裂隙的野外勘探资料建立岩体模型，模拟获得岩体变形模量、抗剪强度参数特征值；盛谦等[3-4]运用弹塑性有限元数值方法研究了三峡船闸区典型地段节理裂隙岩体宏观力学参数的结构效应与强度特征；梁正召等[5]采用细观弹性损伤模型和有限元法(FEM)来实现岩石三维破裂过程的数值模拟；于庆磊等[6]应用数字图像技术对岩石材料细观分布进行精确测量，获得可反映岩石非均匀性的平台巴西盘数值模型；麦戈等[7]基于连续介质力学的方法，引入Weibull随机概率分布表征岩石非均质特性与损伤局部化现象，建立了岩石细观力学模型，对不同摩擦因数下的岩石试件单轴压缩试件进行数值试验分析。离散元数值试验方面，李世海等[8]采用了三维离散元模拟了含节理岩块的单轴压缩试验；程东幸等[9]应用离散元3DEC进行了岩石数值单轴压缩试验、直剪试验以及岩体结构面直剪试验；徐金明等[10]基于非连续介质理论的颗粒流方法，获得了岩体的颗粒接触力、颗粒接触模量、接触连接强度和连接刚度比等细观力学参数。

以上研究方法及成果为数值试验确定围岩力学参数提供了较好的参考与借鉴，但均存在一个典型问题，即：数值试验模拟对象不明确。其模拟与工程实际中不同围岩类别下的岩体结构对应性不佳，这使得模拟结果在工程实际中的参考性受到一定限制。而解决该问题的途径应基于工程实际，依据围岩分类结果选择不同围岩类别代表性结构面网络模型，并进行准确数值建模及数值试验，确定相关力学参数。

本文根据徐光黎等[11]分析分解模型的研究思路，提出一种采用分析分解模型数值试验估算围岩力学参数的新方法，依据围岩分类体系结果，基于圆盘中心点Monte Carlo方法随机分布方法，构建不同围岩类别的三维结构面网络模型；借助试验成果将得到的完整岩块及相关结构面力学参数值作为模型的基本输入参数，并应用有限元法实现对单轴压缩、三轴压缩等试验的模拟，以完成对不同类别围岩力学参数值的确定。本研究可为准确估算不同围岩类别力学参数提供了一条新途径。

2 不同围岩类别对应结构面网络图的构建

岩体结构空间分布特征指标反映了岩体结构空间展布状况，其主要包含结构面组数、产状、迹长、平均间距及连通性等几何形态描述指标。正是由于岩体结构面的空间展布尺寸的增大，岩体质量出现显著降低。本文根据大岗山水电站地下厂房区围岩分类标准，得出了围岩类别与岩体空间分布特征指标的对应关系，如表1。

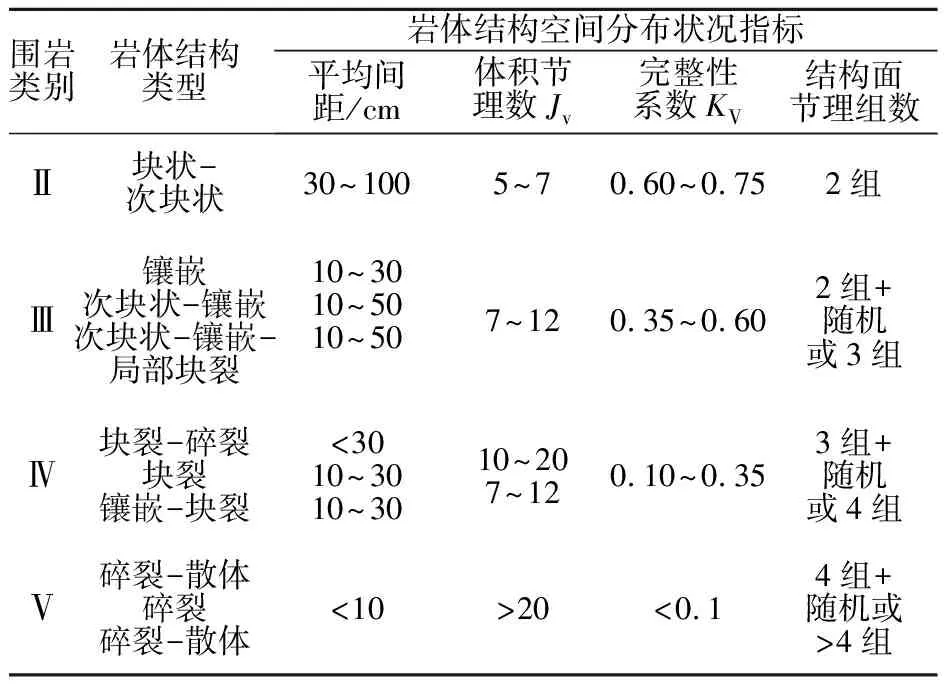
表1 大岗山地下厂房区围岩类别与岩体结构空间分布状况指标对应关系

基于围岩类别与岩体空间分布特征指标对应关系，假定节理形状为薄圆盘状，且节理半径(长度)符合正态分布形式，通过控制结构面间距及组数来实现对圆盘中心点数目的控制。此后，考虑节理岩体尺寸效应代表性单元体积(REV)影响，以Ⅱ类围岩为测试对象，通过选择不同尺寸的立方体范围进行模拟测试，最终从准确性与方便性角度出发，选取10 m×10 m×10 m的立方体范围进行结构面网络图构建，并应用Monte Carlo随机模拟方法实现对节理中心点坐标的空间随机展布。通过控制节理半径、产状来构建其结构面网络图，详细操作应用澳大利亚阿德莱德大学的C. S. Xu和P. Dowd[12]联合开发的三维结构面网络模拟程序FracSim 3D予以实现。

为实现评价结果的对应性，应用FracSim 3D确定节理中心点数目时，均采用该类别对应的中间值进行。以Ⅱ类围岩为例，现应用70 cm间距和2组节理来予以控制，则相应地，对成组的节理长、短半径分别采用4～5 m，2～3 m取值范围处理；而对非成组节理长、短半径分别采用1.5，1.0 m的等效处理方法。节理产状可采用厂房区优势产状组合产状，目前选用5组产状予以三维网络模拟生成。依据产状统计数目排序依次为：N7°E/NW∠67°，N89°E/SE∠78°，EW/N∠81°，N20°W/SW∠75°，N31°E/SE∠17°，故随着围岩类别降低，逐渐启用下一组产状，详细模拟结果见图1(a)。同样，应用上述方法可实现对Ⅲ-Ⅴ类围岩三维结构面网络模拟图的构建，如图1(b)至图1(d)所示。图1中黑色截断面为随机取样面。

图1 Ⅱ—Ⅴ类围岩对应的三维结构面网络图

通过调整截断面的x，y，z坐标方向与大小，随机从三维结构面网络图中截取不同方向上的二维节理图，本文选取从x，y，z3个相互垂直角度中央部位截取断面，并参考135°斜交xy面以反映岩体结构的空间各向异性特征，以Ⅱ类围岩为例，截取不同方向的二维节理分布图(见图2)。同样，亦可从Ⅲ—Ⅴ类围岩三维结构面网络模拟图随机布置截面，截取不同方位的二维节理分布图(见图3)，为下一步进行数值模拟试验提供原始试验几何模型。

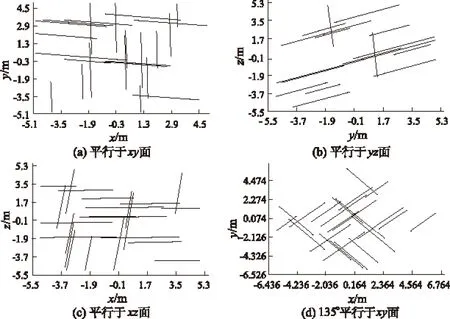
图2 Ⅱ类围岩三维网络图中不同方向截取的节理分布图

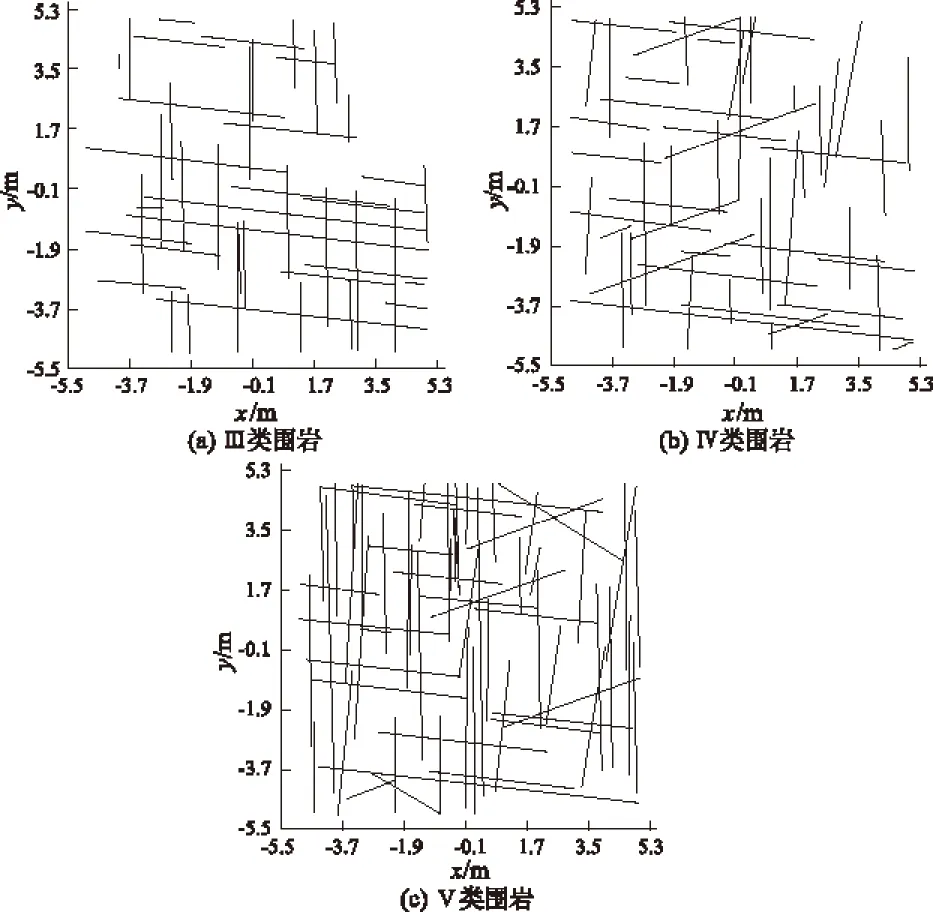
图3 Ⅲ—Ⅴ类围岩三维网络图截取典型二维节理分布图(平行于xy面，z=5处垂直截取)

3 分析分解模型数值试验技术要求

考虑岩体强度、变形的大小体现为岩块与结构面联合抵抗作用的大小，基于有限元数值方法等效模拟节理岩体加载受力过程。首先，应实现对相关边界条件控制，该过程应尽量与现实试验保持一致；此后，试验过程中不断调整围压大小模拟加载、卸载过程，通过观察岩体“试样”位移变化情况来判定“试样”是否发生大变形破坏，记录对应破坏点及加载过程的应力-应变曲线，进而通过相关拟合、判定方法实现对岩体力学参数的确定。本文主要采用Phase 2D程序[13]对Ⅱ—Ⅴ类围岩截取的二维节理分布模型图予以数值试验分析。

3.1 分析分解模型介质本构关系选取标准

3.1.1 完整岩石本构关系的选取

岩石本构关系是建立岩石几何形态与力学性状的重要途径。目前，Mohr-Coulomb模型和Drucker-Prager模型是岩土工程领域常用的2种模型，其中前者在岩石工程应用更为适用，而后者更适用于对软质黏土的模拟；而Hoek-Brown模型、通用Hoek-Brown模型是对岩体变形、破坏状况的经验性模型，相关参数如m，s，a，GSI等的确定需要借助一定人为经验。本文选取最为通用的Mohr-Coulomb模型作为完整岩块本构关系模型。

3.1.2 节理面本构关系的选取

目前，Barton-Bandis模型主要用于对节理剪切强度特征的模拟，需考虑节理的粗糙程度指标JRC和压缩强度指标JCS等；基于现场对随机性结构面粗糙度、壁面强度特征的大量测试，本文应用针对性更强的Barton-Bandis模型实现对结构面本构关系的模拟。

3.2 分析分解模型中介质力学参数确定

基于完整岩块与结构面对应的本构关系模型，结合现场岩体结构精细化描述体系结果，得到完整岩块与结构面各自对应的相关力学参数值。其中节理面Barton-Bandis模型中JRC，JCS值确定方法介绍如下。

粗糙程度指标JRC值大体参考Barton标准轮廓曲线对比法(经验类比法)[14]予以确定。依据杜时贵简易纵剖面仪制作及量测方法，现场设计简易粗糙度量测仪，实测获得随机结构面粗糙度轮廓曲线，与Barton标准轮廓图对比可快速得知对应的节理粗糙度JRC值；而压缩强度指标JCS借助Muller试验获得的回弹实测值R和容重γ与其经验关系式[15]：

lg(JCS)=0.008 8γR+1.01 。

(1)

其中，回弹实测值R依据场回弹仪测试对应的硬性结构面平均值予以选取。据此，得到完整岩块与结构面分别对应的力学参数值如表2所示。

表2 大岗山地下厂房区完整岩块与结构面对应力学参数值

3.3 数值试验加载方式控制

3.3.1 单轴压缩数值试验加载方式控制

利用Phase2D程序进行“试样”单轴压缩数值试验时，考虑结构面的发育对岩体强度控制性作用，若简单照搬室内单轴压缩试验方法，极易出现岩体在不均匀荷载影响下，在较小外力作用下沿结构面的贯通性失稳。故此处采用在其左右边界施加一定的围压作用(0.5 MPa)，在其底部边界通过施加双向位移约束控制，然后，在程序中设置“时间步长”对其上覆逐步施加轴向压力(其中Ⅱ类围岩以2 MPa为初始荷载；此后每步增加2 MPa均布荷载，Ⅲ类围岩以2 MPa为初始荷载，此后每步增加1 MPa；Ⅳ—Ⅴ类围岩以1 MPa为初始荷载，后每步增加0.5 MPa)进行控制，而后根据观察不同步长下对应的位移变形特征来判断“试样”是否已加载破坏。

但考虑本程序自身存在的缺陷，难以实现连续加载，为准确反映单轴压缩试验岩体峰值强度特征，整个试验过程仍按照2 MPa为初始荷载，但在根据其位移变形特征确定其完全破坏后，通过在该2 MPa区间内进行细化加载，将加载步距控制在0.2 MPa，且在某个加载段内出现新增位移较前一个加载段增幅超过50%，即认为“试样”已加载破坏，对应的该区段为岩体应力峰值强度。

3.3.2 三轴压缩数值试验加载方式控制

三轴压缩数值试验按照室内三轴试验方法，首先，在“试样”左右边界施加合适的围压(2 MPa)，接着，开始逐步施加一定的轴向压力，每增加一次，计算其对应的位移和应力。当2个计算步长出现位移差值明显增加，增幅达到50%以上时，可认为试样出现破坏，记录此时对应的σ1-σ3数值； 而后，变换围压作用(每步增加2 MPa均布荷载)，同样进行轴压增加试验直至破坏，记录各自对应的σ1-σ3值。最后，应用记录σ1-σ3值得到一系列应力摩尔圆，推算其对应岩体黏聚力c和内摩擦角φ值。

4 分析分解模型数值试验结果讨论

4.1 单轴压缩数值试验结果

以Ⅱ类围岩平行于xy面，z=5处垂直截取的结构面网络模拟结果为例，通过构建其对应的分析分解模型，而后应用Phase 2D程序进行“试样”单轴压缩数值试验，围压均为0.5 MPa,上覆荷载σy取值范围2～16 MPa，每2 MPa递增。当上覆均布荷载增加至16 MPa时，“试样”相对变形骤增，可认为其大变形破坏，此时对应的均布荷载值可认为是该“试样”对应的单轴抗压强度数值试验值，详细加载过程变形状况见图4。

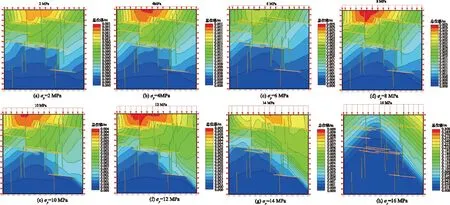
图4 Ⅱ类围岩数值试验加载过程变形状况(平行于xy面，z=5截面)

同样，对Ⅱ-Ⅴ类围岩不同方向截取的结构面网络模拟图进行分析分解模型数值试验，每类岩体进行4个不同方向的单轴压缩数值试验，分别得到各自对应的单轴抗压强度值，汇总结果见图5。

图5 Ⅱ—Ⅴ类围岩单轴抗压强度数值试验结果

由图5可知，不同围岩类别对应的单轴抗压强度值为：Ⅱ类σcm=13.8～18.2 MPa；Ⅲ类σcm=7.8～11.6 MPa；Ⅳ类σcm=1.8～7.4 MPa；Ⅴ类σcm= 1.4～6.2 MPa。

同样，将数值试验与现场估算结果进行对比(表3)发现，Ⅱ-Ⅲ类数值试验结果与抗压强度参数拟合估算式结果大体上吻合，而较Hoek-Brown经验准则，围岩强度特征参数估算结果要总体偏小，这可能与施加的0.5 MPa的“防初始尺度大变形”围压有关，使得测试并非为真正意义上的“单轴试验”。而Ⅳ—Ⅴ类结果较为离散，但数值试验所反映的规律性特征仍较为明显。

表3 不同围岩类别抗压强度σcm数值试验与估算结果对比

4.2 三轴压缩数值试验结果

均选取平行于xy面，z=5处垂直截取的结构面网络模拟图，实现Ⅱ—Ⅴ类围岩分析分解模型三轴压缩数值试验分析，以Ⅱ类围岩分析结果为例，通过不断改变围压得到不同σ1-σ3下对应的系列摩尔应力圆，见图6。

图6 Ⅱ类围岩不同σ1-σ3下对应的摩尔圆

同样，应用数值试验获得Ⅲ—Ⅴ类围岩在不同σ1-σ3下对应的摩尔应力圆，线性拟合可得到其各自对应的黏聚力c和内摩擦角φ值。详细结果Ⅱ类：c=1.85～2.0 MPa，φ=46°～50°；Ⅲ类：c=1.35～1.6 MPa，φ=42°～49°；Ⅳ类：c=0.95～1.2 MPa，φ=39°～44°及Ⅴ类：c=0.50～0.75 MPa，φ=32°～40°。

数值试验与围岩分类估算法结果对比(表4)发现，Ⅱ—Ⅲ类数值试验结果较工程经验统计法、Hoek-Brown经验准则估算结果均整体偏小，而Ⅳ—Ⅴ类较工程经验统计法、Hoek-Brown经验准则结果偏大，即体现为不同围岩类别对应黏聚力c和内摩擦角φ值无显著离散特征。究其原因，一方面与初始分析分解模型有关，Ⅱ—Ⅴ类代表性结构面网络图差异性不甚明显；另一方面，建模过程中，对完整岩块、结构面赋值大体相同，受边界约束条件限制，使得实测结果与现实情况出现不吻合情况，该结果仍有待进一步讨论。

表4 不同围岩类别抗剪强度数值试验与估算结果对比

5 结 论

(1) 提出一种采用分析分解模型数值试验估算不同围岩类别力学参数的新方法，实现基于圆盘中心点Monte Carlo随机分布方法，借助FracSim 3D程序及多方位截取方法构建分析分解模型，该方法可为不同围岩类别力学参数数值试验提供原始数值模型。

(2) 应用地下硐室已有试验成果，将分别得到的完整岩块及相关结构面的力学参数值作为模型基本输入参数，并推荐完整岩块、结构面本构模型分别为：Mohr-Coulomb模型、Barton-Bandis模型。

(3) 单轴数值试验结果显示，Ⅱ-Ⅲ类围岩数值试验结果与抗压强度参数拟合估算结果大体吻合，而较Hoek-Brown准则围岩强度特征参数估算结果要总体偏小；三轴数值试验表明，Ⅱ-Ⅲ类围岩数值试验结果较工程经验统计法、围岩分类准则估算结果均整体偏小，而Ⅳ-Ⅴ类围岩数值试验结果较工程经验统计法、围岩分类准则结果偏大，有待进一步的深入分析。

参考文献：

[1] 胡 波，王思敬，刘顺桂，等. 基于精细结构描述及数值试验的节理岩体参数确定与应用[J]. 岩石力学与工程学报，2007，26(12)：2458-2465.(HU Bo，WANG Si-jing，LIU Shun-gui，etal. Determination and Application of Jointed Rock Mass Parameters Based on Fine Structure Description and Numerical Experiment[J]. Chinese Journal of Rock Mechanics and Engineering，2007，26(12)：2458-2465. (in Chinese))

[2] 周维垣，杨延毅. 节理岩体力学参数取值研究[J]. 岩土工程学报，1992，14(5):1-11.(ZHOU Wei-yuan, YANG Yan-yi. A Computer Simulation Method to Predict the Mechanical Properties of Jointed Rockmass[J]. Chinese Journal of Geotechnical Engineering, 1992,14(5):1-11. (in Chinese))

[3] 盛 谦，黄正加，邬爱清. 三峡节理岩体力学性质的数值模拟试验[J]. 长江科学院院报，2001，18(1)：35-37. (SHENG Qian, HUANG Zheng-jia，WU Ai-qing. Numerical Simulating Test on Joint Rock Mass Properties in Three Gorges Project[J]. Journal of Yangtze River Scientific Research Institute, 2001，18(1):35-37. (in Chinese))

[4] 周火明，盛 谦. 三峡工程永久船闸边坡岩体宏观力学参数的尺寸效应研究[J]. 岩石力学与工程学报，2001，20(5):661-664. (ZHOU Huo-ming，SHENG Qian. Size Effect Analysis on Macro-Mechanics Parameters for the Rock Masses of the TGP Shiplock Slop[J]. Chinese Journal of Rock Mechanics and Engineering, 2001，20(5):661-664. (in Chinese))

[5] 梁正召，唐春安，李厚样，等.单轴压缩下横观各向同性岩石破裂过程的数值模拟[J]. 岩土力学，2005，26(1)：57-64. (LIANG Zheng-zhao, TANG Chun-an, LI Hou-xiang，etal. A Numerical Study on Failure Process of Transversely Isotropic Rock Subjected to Uniaxial Compression[J]. Rock and Soil Mechanics, 2005，26(1)：57-64. (in Chinese))

[6] 于庆磊，唐春安，杨天鸿，等. 平台中心角对岩石抗拉强度测定影响的数值分析[J]. 岩土力学，2008，29(增2)：3251-3260.(YU Qing-lei, TANG Chun-an, YANG Tian-hong,etal. Numerical Analysis of Influence of Central Angle of Flats on Tensile Strength of Granite in Split Test with Flattened Disk[J]. Rock and Soil Mechanics，2008，29(Sup.2):3251-3260. (in Chinese))

[7] 麦 戈，唐照平，唐欣薇. 岩石单轴压缩端部效应的数值仿真分析[J]. 长江科学院院报，2013，30(6)：68-71. (MAI Ge，TANG Zhao-ping，TANG Xin-wei. Numerical Simulation of Rock’s End Constraint Effect under Uniaxial Compression[J]. Journal of Yangtze River Scientific Research Institute，2013，30(6)：68-71.(in Chinese))

[8] 李世海，董大鹏，燕 琳. 含节理岩块单轴受压试验三维离散元数值模拟[J]. 岩土力学，2003，24(4)：648-652. (LI Shi-hai, DONG Da-peng, YAN Lin. 3D-DEM Numerical Simulation for Jointed Rock under Uniaxial Compression[J]. Rock and Soil Mechanics, 2003，24(4):648-652. (in Chinese))

[9] 程东幸，潘 炜，刘大安, 等. 锚固节理岩体等效力学参数三维离散元模拟[J]. 岩土力学，2006，27(12)：2127-2132. (CHENG Dong-xing, PAN Wei, LIU Da-an,etal. 3DEC Modeling of Equivalent Mechanical Parameters in Anchored Jointed Rock Mass[J]. Rock and Soil Mechanics, 2006，27(12):2127-2132.(in Chinese))

[10] 徐金明，谢芝蕾，贾海涛. 石灰岩细观力学特性的颗粒流模拟[J]. 岩土力学，2010，31(增2):390-395. (XU Jin-ming, XIE Zhi-lei, JIA Hai-tao. Simulation of Mesomechanical Properties of Limestone Using Particle Flow Code[J]. Rock and Soil Mechanics，2010，31(Sup.2):390-395. (in Chinese))

[11] 徐光黎，潘别桐，晏同珍. 节理岩体变形模量估算新方法[J]. 地球科学：中国地质大学学报，1991，16(5)：573-580. (XU Guang-li, PAN Bie-tong, YAN Tong-zhen. A New Method for Evaluate of Moduli of Jointed Rock Mass[J]. Earth Science：Journal of China University of Geosciences, 1991，16(5):573-580.(in Chinese))

[12] XU C S，DOWD P. A New Computer Code for Discrete Fracture Network Modelling[J]. Computers and Geosciences，2010，36(3)：292-301.

[13] HORK E. Phase2.7 Modeler (Version 7.013) [EB/OL]. (2010-02-10) [2013-12-20]. http://www.rocscience.com.

[14] BARTON N, BANDIS S. Review of Predictive Capabilities of JRC-JCS Model in Engineering Practice[J]. Publikasjon-Norges Geotekniske Institutt, 1991, 182: 1-8.

[15] 杜时贵. 岩体结构面抗剪强度经验估算[M].北京：地震出版社，2005.(DU Shi-gui. Empirical Estimation of Shear Strength for Structural Planes of Rockmass[M]. Beijing：Earthquake Press, 2005.(in Chinese))

[16] GB50218—94，工程岩体分级标准[S]. 北京：中国计划出版社，1995.(GB 50218—94，Standard for Engineering Classification of Rock Masses[S]. Beijing：China Planning Press，1995. (in Chinese))

[17] GB50287—2006，水力发电工程地质勘察规范[S]. 北京：中国计划出版社，2006.(GB 50287—2006，Code for Hydropower Engineering Geological Investigation [S]. Beijing：China Planning Press，2006. (in Chinese))