“大地测量学基础”课程启发法教学几个问题的解释

丁士俊，郭际明，程新明，向 东

(武汉大学 测绘学院，湖北 武汉 430079)

一、引 言

大地测量学是地球科学的重要学科分支之一，它是大地测量、工程测量、摄影测量与遥感、地图以及地理信息等专业的基础学科。在大地测量、工程测量、摄影测量与遥感等相关测绘专业合并为一个测绘专业的背景下，面对测绘技术与测绘教育的新形势，按照全国测绘教学指导委员会关于编写测绘工程专业系列基础教材的计划和要求，《大地测量学基础》是专为测绘工程专业本科生编写的一门基础性教材。该教材以现代大地测量学理论体系为基础，以现代大地测量学的新成就和未来发展为出发点，正确处理好经典内容和现代发展的关系，全书以传统应用大地测量学、椭球大地测量学、控制测量学等多种版本教材为基础，以几何大地测量学、物理大地测量学及现代空间大地测量学为基本体系框架的基础上编写的，教材大量删减了过时的内容，引进最新的大地测量新成果，提出未来发展方向，较为系统地阐述了大地测量学的基本概念、基本理论和测量技术与方法。通过近几年的教学情况来看，为了克服以往填鸭式的教学模式，充分利用学生已掌握的知识，开展启发式教学，充分调动学生的自主学习的积极性，培养学生分析问题、解决问题的能力，提高教学质量,有针对性对一些相关问题探讨启发式教学方法与教学内容，本文通过以下几方面对此加以讨论。

二、课堂教学与课外自主学习的统一

在大地测量教学过程中，对于基本概念、基本理论、基本技术方法在课堂上要加以充分讲解，把教学内容分为基本内容、选学内容和自学内容。其次突出重点难点，对于重点内容要讲深讲透，难点内容主要从提出问题、分析问题及解决问题的方法入手，让学生了解其过程，理清其思路。突出科学思维辩证逻辑方法，以素质教育培养学生的能力为目的，调整课堂的教学方式与方法。过去在教学内容与时间基本相符的情况下，课堂的教学基本上是填鸭式的教学模式。为了提高学生学习的主动性与创造性，改变过去那种一统式的教学方式，将教学内容与时间分为老师主讲课、学生自学、讨论课等部分，在自学与讨论课的环节中，其内容要有针对性，教师在教学的过程中要积极加以组织，学生是学习的主体，教师起到引导、解疑、归纳的作用，这样在激发学生学习主动性的同时，学生对相关知识的理解得到了进一步的深化，拓宽了视野。下面仅以教材中两个知识点的教学加以阐述。

1. 大地坐标与空间直角坐标的关系

在空间大地测量数据处理中，空间直角坐标与空间大地坐标的相互关系是大地测量数据处理的一个最基本而最为重要的关系式。在《大地测量学基础》教材中，首先建立子午平面直角坐标与大地坐标的关系，然后确定空间直角坐标与子午平面直角坐标的关系，通过子午平面直角坐标过渡，最后得到椭球面上点P0的空间直角坐标(X,Y,Z)与大地坐标(B,L)的关系[1-2](如图1所示)

(1)

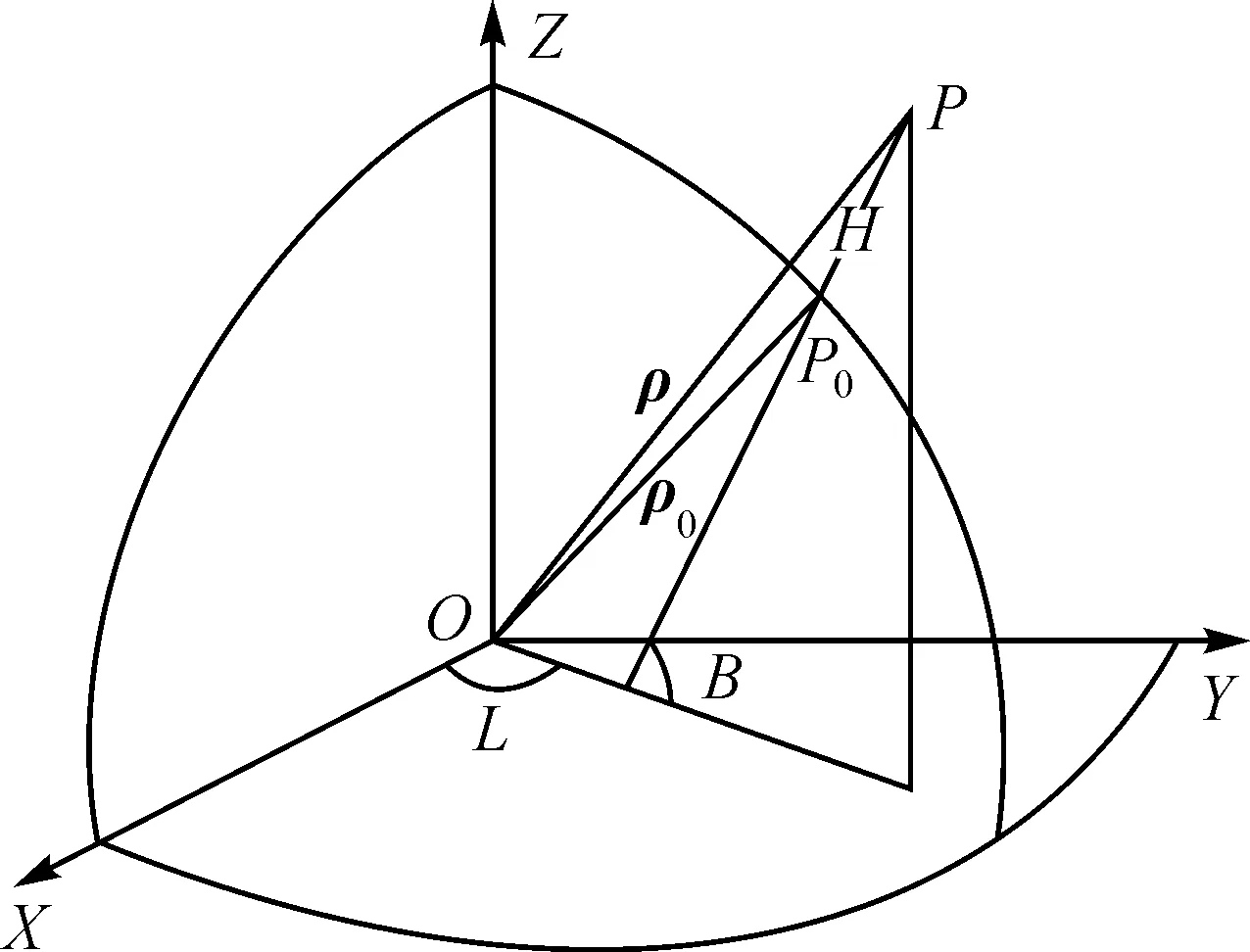
图1 空间直角坐标与大地坐标关系

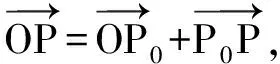
ρ=ρ0+Hn

(2)

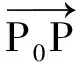
(3)

方法2：因为法线垂直于过P0点椭球的切平面，切平面包含过P0子午线的切线与平行圈的切线，因此法线垂直于该点子午线的切线与平行圈的切线，只要求出过该点子午线的切线与平行圈的切线的单位向量，即可求出过P0点法线的单位向量。基于上述思想，根据椭球面参数方程式(1)，分别固定大地经度与大地纬度，即可得到子午线与平行圈空间的参数方程，分别对各自的参数方程求导，得到子午线与平行圈在P0的切线的单位向量，假设子午线在P0点切线的单位向量为nB,平行圈在该点的切线的单位量为nL,则过P0点法线的单位向量n为[1]

n=nB×nL

(4)

式中，|nB|=(sinBcosL-sinBsinLcosB)；|nL|=(cosBsinLcosBcosL0)。由式(4)同样可得到式(3)的结论。由式(1)—式(3)联立得到地面点大地坐标与空间直角坐标的关系式

(5)

2. 子午线曲率半径的计算

为了让学生充分利用自身所掌握的知识与基本理论，来解决专业课程中的一些理论问题，就子午线曲率半径的计算问题，除了采用教材中所介绍的方法之外，在教学过程中启发学生，利用所掌握的高等数学知识来解决子午线曲率半径的计算。由高等数学可知，已知某曲线方程y=f(x)，则曲线任意点的曲率半径k可由式(6)来加以计算[2]

(6)

在旋转椭球体子午面内，子午线曲线方程可由直角坐标来描述，即

(7)

也可采用大地纬度B或归化纬度u的参数方程来加以表达[3-4]

通过对表3实验数据的分析，随着脂肪添加量的增加，薏米鸡肉饼的亮度、红度、黄度均呈现先变大后变小的趋势。观察薏米鸡肉饼的色泽也是由金黄色逐渐到红棕色的变化。脂肪可以影响肉制品的光泽度和口感，当脂肪添加量为10.0%时，薏米鸡肉饼的色泽光亮，口感柔和。由此可以确定脂肪最佳添加量为10.0%。

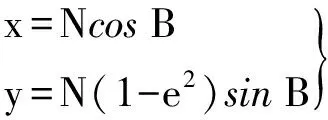
(8)

显然，子午线曲率半径的计算可分别对式(7)或参数方程式(8)分别求导来加以计算。以归化纬度u为参数的参数方程为例，对该参数方程求导一阶和二阶导数，即得到

(9)

(10)

将式(9)与式(10)代入式(6)得

(11)

(12)

由此从另一思路导出了大地坐标与空间直角坐标及椭球面子午线曲率半径的计算公式。上述两方面的内容在教材中都没有涉及，在教学中可引导学生加以思考，或以讨论课的形式来加以讨论，让学生加深对此问题的理解与掌握。

三、 实验教学与理论教学的相互补充

实验教学是教学的又一重要环节，通过实验可以明确对理论掌握的准确度，进一步加深对理论问题的理论与掌握。从多年的教学情况来看，由于课程的内容较多，教学的学时相对较短，在教学的过程中，往往会忽略一些知识点细节性的问题介绍。如在本课程的教学中，通常情况下设有4学时的编程计算课，主要完成“大地测量学基础”课程中一些常见的基本计算，如大地坐标与空间直角坐标的相互换算、大地主题的正反算(平均高斯引数法与白塞尔方法)、高斯投正反算与邻带换算、不同平面坐标系之间的坐标转换、不同空间三维坐标系的转换(包括不同ITRF框架间的相互转换)等。通过编程计算练习，一方面可以帮助学生加深对理论的理解，另一方面可以提高学生解决实际问题的能力，帮助学生认识到自己在学习中存在的问题与不足。根据多年教学经验，主要存在以下问题：一是由于课堂理论教学对于一些知识点细节性的问题介绍得不够，造成了学生对计算问题往往考虑得不够全面；二是教材中个别问题的数学模型不够精确；三是学生对计算数据的精度把握不够准确。本文针对上述问题从以下几方面加以说明。

1. 由空间直角坐标计算大地坐标应注意的问题

随着空间科学的发展，各种卫星如地球同步卫星、GPS卫星等的广泛应用，卫星在空间的瞬时位置在地心空间坐标系中可由大地坐标或空间直角坐标表示，因此大地坐标与空间直角坐标的相互换算应用非常广泛。由空间直角坐标计算大地坐标是一个相对复杂的计算问题，到目前为止，为了解决该问题许多大地测量工作者作了大量的研究，提出了许多算法，已有的算法归结起来可分为迭代法与直接解法[5]。在《大地测量学基础》教材中仅介绍了一种迭代方法，其具体模型如下[3-4]：

大地经度计算

(13)

大地纬度的迭代计算

(14)

大地高的计算

(15)

(16)

在实验课程计算中，由于教材对计算的一些细节问题没有加以介绍，教师在授课时也往往会忽略。如计算时要考虑通用性，其主要表现在适合整个地球体及点高出椭球面、低于椭球面、点位于赤道，以及椭球旋转轴方向等特殊情况，对于这些计算的细节问题必须要全面加以考虑，只有这样所编写的程序才会顾及各种不同的情况，这些问题学生一般难以考虑到，只有通过实验引导与启发学生如何来加以解决，这样可以弥补课堂上理论教学的不足。就上述计算而言，大地经度的计算涉及象限的判断

(17)

(18)

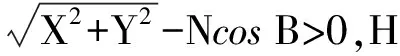
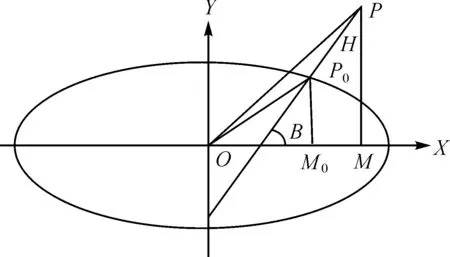
图2 地面点大地经纬度与大地高示意图

2. 高斯平均引数法大地主题解算问题

在《大地测量学基础》教材大地主题解算章节中，根据大地线长短，把大地主题解算分为短距离(400 km以内)，中距离(400～1000 km)及长距离(1000 km以上)3种，教材中所介绍的高斯平均引数法和白塞尔方法分别适合于短距离与长距离解算。实验计算表明，高斯平均引数法解算精度按照教材中现有模型计算，在400 km附近达不到要求，通过与白塞尔方法对比计算，可以让学生进一步明确高斯平均引数法解的适用范围，这一点在课堂理论教学中没有得到体现，只有通过实验计算才有一个比较明确的认识。另外通过计算表明，在旧版《大地测量学基础》教材中[3]，高斯平均引数法反算数学模型不够准确，在新版教材中[4,6]给出改进计算公式，即

(19)

按照上述公式解算，大地线长度在200 km范围内满足计算精度要求。

3. 实验数据的有效数位的确定

“大地测量学基础”课程实验计算中，已知数据与计算数据包括大地经度与大地高(B,L,H)、空间直角坐标(X,Y,Z)以及高斯平面坐标(x,y)等。在计算过程中，各数据的取位(即有效数字的位数确定)问题，学生一般难以把握，通常可以从以下关系式来加以解释。由高斯投影正算可知，高斯投影正算已知大地经纬度(B，L)计算高斯平面坐标(x,y)，对高斯投影正算公式求导，可得到如下微分公式[4，7]

(20)

式中各系数为

(21)

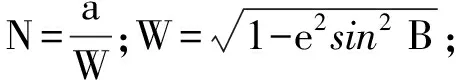
四、结束语

“大地测量学基础”课程2009年被评为国家精品课程，笔者积极进行了该课程的理论教学与实验教学探索，探讨启发式教学的新模式、新方法与新内容，使理论教学与实验教学更紧密地结合在一起。通过实验教学，可弥补课堂理论教学的不足，解决理论教学中存在的一些问题，发挥学生的主观能动性，提高学生自主学习的能力与分析问题、解决问题的能力，使本科教学上一个新的层次，尤其是在提高教学质量等方面具有非常重要的作用和指导意义。

参考文献：

[1] 施一民. 现代大地控制测量[M]. 北京: 测绘出版社, 2003.

[2] 潘映川. 高等数学讲义[M]. 北京: 人民出版社，1981.

[3] 孔祥元,郭际明. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2005.

[4] 孔祥元,郭际明. 大地测量学基础[M].2版. 武汉: 武汉大学出版社, 2010.

[5] 李延兴，张静华，张俊青，等. 一种由地心直角坐标到大地坐标的直接转换[J]. 大地测量与地球动力学, 2007,27(2)：37-42,46.

[6] 郭际明, 丁士俊. 大地测量学基础实践教程[M]. 武汉: 武汉大学出版社, 2009.

[7] 丁士俊. 工程三维网与GPS基线向量的联合处理[D].武汉：武汉大学, 1993.

[8] 陈健, 晁定波. 椭球大地测量学[M]. 北京: 测绘出版社, 1989.

[9] 朱华统, 黄继文. 椭球大地计算[M]. 北京: 八一出版社, 1993.

[10] 丁士俊, 郭际明, 刘宗权，等. 大地测量学基础课程教学与实践改革研究[J]. 测绘工程, 2007, 16(1), 73-75.

[11] 邱卫宁, 王新洲，陶本藻. 测量平差教学体系的设计与研究[J]. 测绘通报, 2006(2)：67-69.