总体最小二乘平差方法在GPS高程拟合中的应用研究

龚循强，陈 磬，周秀芳

(1. 西南交通大学 地球科学与环境工程学院，四川 成都 611756； 2. 江西省数字国土重点实验室(东华理工大学)，江西 南昌 330013； 3. 四川省应急测绘保障与地质灾害监测工程技术研究中心，四川 成都 610041； 4. 江西核工业测绘院，江西 南昌 330038； 5. 四川农业大学 经济管理学院，四川 成都 611130)

一、引 言

GPS高程拟合是将高程异常值与平面坐标近似描述为多项式关系，利用同时已知大地高和正常高的公共点组成误差方程，进而求解多项式系数。目前，普遍采用最小二乘(LS)求解GPS高程拟合的多项式系数，该方法具有简单、方便等优势，但也同样存在未顾及系数矩阵误差这一客观现象。基于此，已有相关学者采用能够同时顾及系数矩阵和观测向量误差的总体最小二乘[1-2](TLS)平差方法进行参数估计，从而使得估计结果更加精确。文献[3]采用基于迭代法的TLS求解参数估值，其实质等同于基于奇异值分解的总体最小二乘(SVD-TLS)，该方法存在未考虑系数矩阵部分有误差的情况，且现今较多文献[4-6]对TLS的求解都是考虑系数矩阵中的全部误差，而在测绘实践中，经常会遇到方程式系数矩阵部分有误差的情况，这种情况需采用混合总体最小二乘(LS-TLS)求解。

近年来，关于GPS高程拟合方法的研究较多[7-8]，而对拟合模型的最佳解算方法却较少涉及。本文在对TLS平差方法进行理论研究的基础上，针对LS和SVD-TLS存在对模型系数矩阵和观测向量误差估计不合理，造成估计结果不严密的现象，尝试采用LS-TLS进行GPS高程拟合，在合理考虑系数矩阵和观测向量误差的情况下，利用本文提出的基于TLS平差的粗差探测方法进行粗差剔除后，对GPS高程拟合参数进行求解。最后结合真实数据，分别利用LS、SVD-TLS和LS-TLS进行GPS高程平面拟合，并对拟合结果进行了比较分析。

二、总体最小二乘平差方法

目前，LS是对拟合函数参数求解的最常用方法，但这种方法不能顾及系数矩阵中的误差。而TLS平差方法能够同时顾及观测向量和系数矩阵误差，使得函数的解算结果更合理。

1. 基于奇异值分解的总体最小二乘

奇异值分解是线性代数中一种重要的矩阵分解，同时也是对TLS参数估计的常用方法，能较好地处理病态矩阵问题。在函数模型中同时顾及系数矩阵和观测向量误差，设矩阵方程为

(A+ΔA)X=L+ΔL

(1)

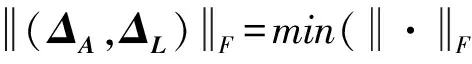
假设观测次数为n，参数个数为m，通常情况下n>m，将增广矩阵B=[AL]奇异值分解为B=UΣVT，SVD-TLS的解可由增广矩阵右奇异向量的最后一列求得，进一步可以计算得到残差平方和及单位权中误差。

2. 混合总体最小二乘

由式(1)可以看出，SVD-TLS求解参数的同时考虑了观测向量和系数矩阵中的全部误差。然而在测绘实践中，经常会遇到系数矩阵部分有误差的情况，若采用SVD-TLS求解显然是不严密的，目前解决这类问题的适宜方法是LS-TLS。假设A1没有误差影响，则顾及系数矩阵和观测向量误差，LS-TLS函数模型为

A1X1+(A2+ΔA2)X2=L+ΔL

(2)

3. 基于总体最小二乘平差的粗差探测方法

TLS平差是研究数据拟合的有效方法，其不仅考虑到观测向量含有误差，同时也考虑到系数矩阵含有误差的情况，反映了观测向量和系数矩阵的总体数据特征。因此，不管对于二维数据拟合还是对于多维数据拟合，总体数据的态势都将在直线或平面一定范围内出现。对于总体观测数据来说，如果有某一个观测量含有粗差或异常值，则该观测数据必定相对于其他数据离拟合的直线或平面的距离要大。

由于TLS平差所形成的拟合直线或拟合平面反映的是总体观测数据的变化趋势，因此，如果观测数据中没有粗差或异常值，基于TLS平差所形成的拟合残差必定分布于某个误差椭圆内。若某个观测数据拟合残差超出了这个误差椭圆，则可以认为此观测数据有可能含有粗差或异常值。基于该思想可以利用TLS拟合残差及极限误差的相关特性探寻观测数据中的粗差或异常值。下面以平面拟合为例进行具体详解，步骤如下：

1) 设有平面方程z=a+bx+cy，利用TLS平差对其进行拟合，求出参数的估计值。

2) 求出中误差σ，并取置信区间为(-2σ,2σ)。

3) 求出拟合残差Vi，判定每一个拟合残差是否在置信区间内。

4) 若拟合残差超出置信区间，则可认为形成该拟合残差的观测数据中含有粗差，可以将其剔除；反之，则认为数据中不存在粗差。

三、实例分析

以上简要阐述了采用LS、SVD-TLS和LS-TLS进行参数估计及精度评定的方法，并给出了基于TLS平差的粗差探测方法。下面采用真实数据进行GPS高程平面拟合，分别利用LS、SVD-TLS和LS-TLS进行计算，并从模型、参数估值、残差平方和及单位权中误差等几个方面对各自的GPS高程拟合结果进行比较分析。

以文献[11]例5.8中的GPS水准拟合观测数据作为样本，并在数据中加入一定的粗差，观测数据见表1，选取测站点的坐标为自变量(x,y)，各点的高程异常值作为因变量δh，则有δh=a+bx+cy。

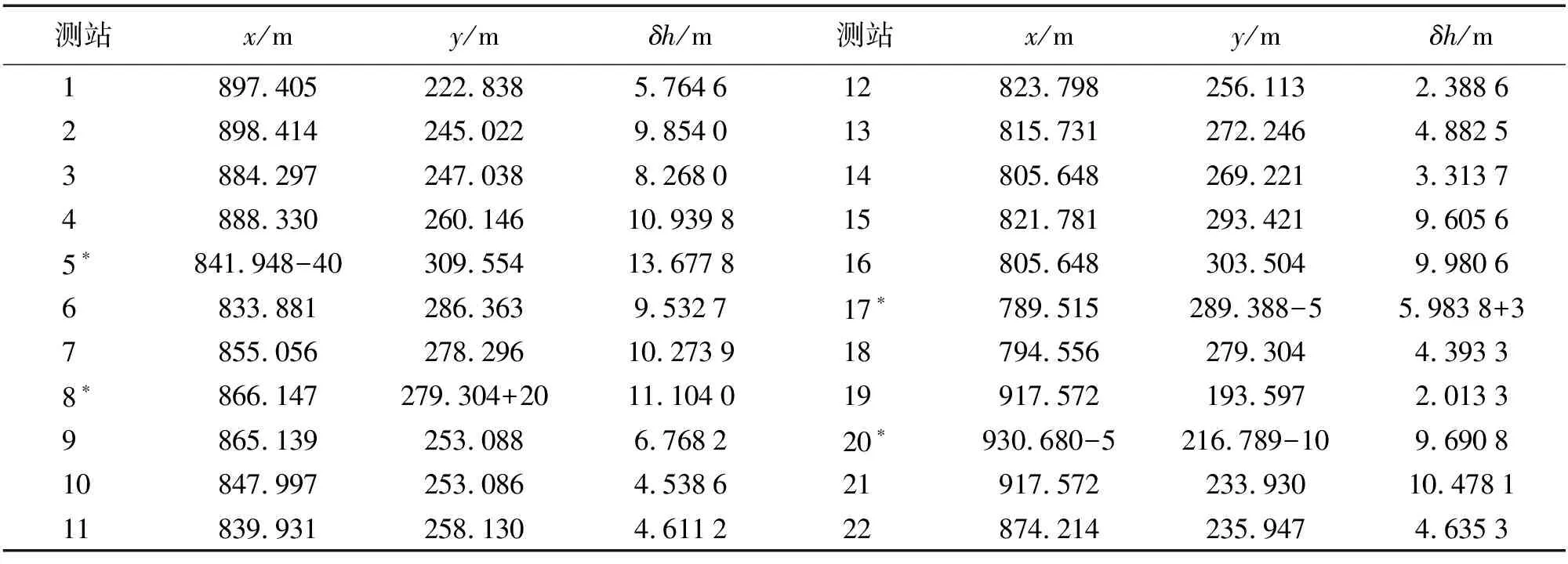
表1 加入粗差后的GPS水准拟合观测数据

由于该平面方程系数矩阵部分含有误差，因此采用LS-TLS求解拟合参数，根据本文提出的基于TLS平差的粗差探测方法进行粗差的探测与剔除。由参数估计值求得中误差σ=1.695 8，即得置信区间为(-3.391 6,3.391 6)，并求出拟合残差Vi，各测站点的拟合残差如图1所示。

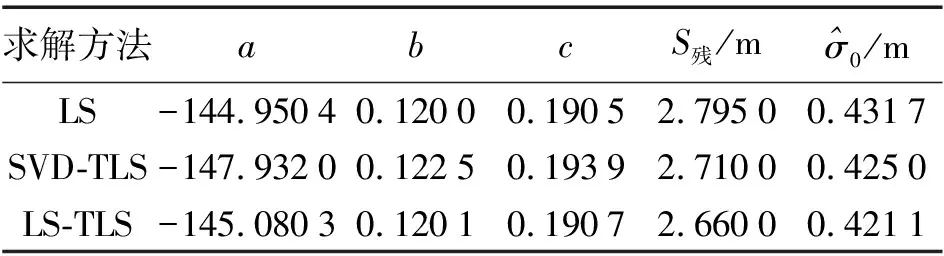
判定每个测站点的拟合残差是否在置信区间内，对存在粗差的测站数据进行剔除，根据图1及求出的置信区间可将5、8、17、20测站数据剔除。同时采用LS、SVD-TLS和LS-TLS 3种方法对剔除粗差后的GPS水准拟合数据进行平面拟合，求出拟合参数、残差平方和及单位权中误差，结果见表2。

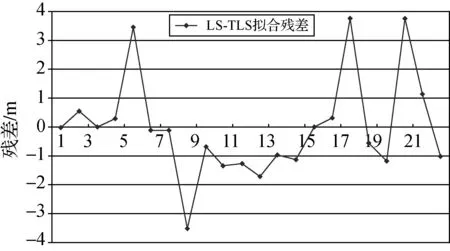
图1 测站点的LS-TLS拟合残差

求解方法abcS残/m^σ0/mLS-144.95040.12000.19052.79500.4317SVD-TLS-147.93200.12250.19392.71000.4250LS-TLS-145.08030.12010.19072.66000.4211

表2中分别采用LS、SVD-TLS和LS-TLS求解了拟合平面参数，由于TLS平差方法同时顾及了系数矩阵x、y和观测向量δh的误差，因此建立的模型更加符合实际情况，其模型的残差平方和及单位权中误差优于LS。

从平面方程δh=a+bx+cy可以看出，部分系数矩阵和观测向量都是由GPS数据组成的矩阵，采用LS进行平面拟合，其只顾及了观测向量δh的误差，因此拟合的平面并不精确；采用SVD-TLS进行平面拟合，所得拟合平面与LS和LS-TLS的拟合平面相差较大，通过分析构建的函数模型和解算方法发现，SVD-TLS将系数矩阵中不存在误差的常数项部分也考虑了进去，因而造成拟合结果变异；LS-TLS合理地顾及了系数矩阵x、y和观测向量δh的误差，因此建立的模型更加合理，所得拟合精度最优，较LS和SVD-TLS拟合平面结果更加接近实际，故可认为合理考虑系数矩阵和观测向量误差的LS-TLS拟合平面结果最为可靠。

四、结 论

本文采用TLS平差方法进行GPS高程拟合，在利用提出的基于TLS平差的粗差探测方法进行粗差剔除的基础上，结合真实数据，进行拟合平面的参数计算及精度评定。通过LS、 SVD-TLS和LS-TLS的比较分析研究，得出如下相关结论：

1) 采用本文提出的基于TLS平差的粗差探测方法能较好地对数据中存在的粗差进行探测与剔除。

2) 在GPS高程拟合参数估计中，由于LS没有考虑系数矩阵存在误差的情况，因此拟合结果并不严密。SVD-TLS 将系数矩阵中不含误差的常数矩阵进行考虑，造成拟合结果变异。

3) 采用LS-TLS进行GPS高程拟合参数估计，它同时合理地顾及系数矩阵和观测向量误差，所得拟合精度最优，因此可认为LS-TLS拟合平面的结果最为可靠。

参考文献：

[1] GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal Numerical Analysis, 1980, 17(6): 883-893.

[2] VAN HUFFEL S，LEMMERLING P. Total Least Squares and Error-in-variables Modeling: Analysis, Algorithms and Applications [M]. Netherlands:Springer,2002.

[3] 赵辉, 张书毕, 张秋昭. 基于加权总体最小二乘法的GPS高程拟合 [J]. 大地测量与地球动力学, 2011, 31(5): 88-90.

[4] 龚循强, 李通, 陈西江. 总体最小二乘法在曲线拟合中的应用[J]. 地矿测绘, 2012, 28(3): 4-6.

[5] 官云兰, 周世健, 张立亭，等. 稳健整体最小二乘直线拟合[J]. 工程勘察, 2012,40(2): 60-62.

[6] 官云兰, 刘绍堂, 周世健，等. 基于整体最小二乘的稳健点云数据平面拟合 [J]. 大地测量与地球动力学, 2011, 31(5): 80-83.

[7] 丛康林, 岳建平. 基于SVR的GPS高程拟合模型研究[J]. 测绘通报, 2011(2): 8-11.

[8] 朱东铭, 秦伟, 范百兴. GPS桥梁控制网高程拟合及其精度分析[J]. 测绘通报, 2009(9): 42-44.

[9] VAN HUFFEL S, VAN DEWALLE J. The Total Least Squares Problem：Computational Aspects and Analysis [M].Philadelphia: Society for Industrial and Applied Mathematics,1991.

[10] GOLUB G H, HOFFMAN A, STEWART G W. A Generalization of the Eckart-Young-Mirsky Matrix Approximation Theorem [J]. Linear Algebra and Its Applications, 1987, 88/89: 317-327.

[11] 邱卫宁, 陶本藻, 姚宜斌，等. 测量数据处理理论与方法[M]. 武汉: 武汉大学出版社, 2008.