DDA块体接触开-闭迭代研究

，，

(长江科学院 水利部岩土力学与工程重点实验室, 武汉 430010 )

1 研究背景

石根华博士提出的非连续变形方法(DDA)，是继关键块体理论后研究块体系统的一种新的计算方法[1-2]。该方法通过满足块体系统力系的平衡、开-闭迭代及动力求解收敛，来获得块体系统力与变形真解。其自提出以来，一直作为岩土工程数值模拟方法研究中的前沿问题，为国内外所重视[3-11]。

非连续变形分析方法是一种隐式求解的动力学计算方法，其中块体接触理论是DDA的核心问题。由于块体系统的接触是一个高度非线性问题，涉及参数众多，如接触面上的弹簧刚度、块体的弹性模量、时间步长等。关于块体系统接触以及合适参数的取值等问题的研究，长期以来，主要借助DDA程序运行和具体问题分析，通过参数组合和试算等方式来获取一些经验性认识。在某种条件下，建立一个解析的理论模型，来反映DDA计算过程中块体接触位移与上述参数间的关系，无疑是非常有意义的。本文试图通过建立2块体接触分析模型，在一定的力学条件下，推导块体间接触位移的理论公式。根据接触位移解析解，对块体系统间块体接触开-闭迭代的过程以及参数间影响规律进行研究，以揭示DDA中块体系统开-闭迭代收敛的本质要求。

由于刚度矩阵组装和联立方程组求解较复杂，本文块体接触分析模型中，仅考虑2个规则的矩形块体接触，下部块体固定，上部块体受均匀分布的铅直向载荷作用。因此，在该模型中，可只考虑法向嵌入这种情况，这样仅涉及到法向刚度弹簧，整个计算过程可以手工完成，而且所得到的结果是解析的。建立了位移解析计算式后，便可以从量化的角度去研究时间步长、块体弹性模量以及弹簧刚度等控制性参数之间的关系及其对计算结果的影响规律。根据本文的解析，证明了石根华博士在DDA计算中采用时间步长来调整和加快开-闭迭代收敛的策略是合理、高效的。该研究也揭示DDA各参数取值应依据的基本规律，可以推动DDA的实际工程应用。

2 DDA块体接触开-闭迭代分析模型

为定量研究DDA块体接触开-闭迭代的本质问题，这里建立了如图1所示的2块体接触开-闭迭代的块体接触分析模型。在该模型中，假定块体N固定，块体M的边长为a,上部边界受到均布荷载σ的作用，其变形模量为E。

图1 块体接触开-闭迭代分析模型

应用该模型推导各项刚度子矩阵和载荷子矩阵，从而形成DDA总体方程，来求解2个块体系统的接触位移。另外，从解析角度研究块体接触部位的变形与块体系统各控制参数间的关系，包括块体的变形模量E、时间步长Δ、弹簧刚度p等参数。

3 DDA块体接触位移理论公式推导

非连续变形分析(DDA)是以严格遵循经典力学规则为基础的。该方法是在假定块体位移模式条件下，利用势能最小原理建立块体系统总体平衡方程。

3.1 二维DDA方法的一阶位移形式

DDA方法做了如下假设：块体的大位移和大变形是由块体每步的小位移、小变形积累得到的。在每个时步内，各块体的位移足够小，块体的物理方程满足弹性力学假定。在一阶位移模式条件下，每个块体内应力、应变均为常应力、常应变。块体的未知量列阵D由以下6个变形变量组成，即D=(u0v0γ0εxεyγxy)T。其中：(u0,v0)为块体内指定点(x0,y0)处的刚体位移；γ0为块体运动时以点(x0,y0)为中心的转动角(弧度)；(εx,εy,γxy)分别为块体的正应变和剪应变。点(x0,y0)一般设为块体的重心。

根据块体运动学方程，块体i内任意点(x,y)的位移(u,v)可由位移转置矩阵Ti和变形变量矩阵Di表示，即

(1)

式中：

Ti=

Di=[d1id2id3id4id5id6i]T=

[u0v0γ0εxεyγxy]T。

3.2 块体系统子矩阵

由于块体N为固定块体，则块体N变形变量的6个分量为0，即

D2=

(u2v2r2εx2εy2γxy2)T=(0 0 0 0 0 0)T

综上，总体方程中只需要形成刚度系数矩阵K11、载荷矩阵F1、变形变量矩阵D1即可。而根据上述已知条件，将块体的惯性子矩阵、弹性子矩阵、弹簧刚度子矩阵和载荷子矩阵总体集成，形成总体方程。其各子矩阵推导如下。

3.2.1 惯性力子矩阵

记(u(t)，v(t))为块体i中任意点(x，y)的随时间变化的位移，m为块体单位面积质量，则块体单位面积惯性力为

(2)

块体i的惯性力势能为

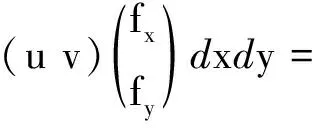
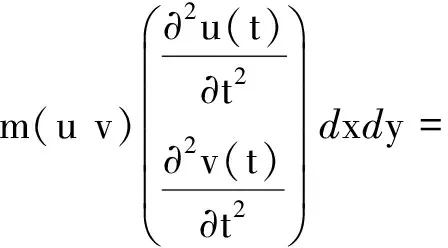
(3)

假定D(tk)为第k时间步开始时位移，Δ为时间步长，Dk为该时步的位移增量，则根据时间积分可以求得

(4)

由此得

(5)

(6)

根据总势能最小，对∏i求导，可得到相应的惯性力子矩阵：

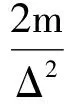
(7)

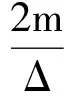
(8)

经计算分析可得

∬TiTTidxdy=

(9)

式中：s为块体面积；s1,s2,s3为中间变量，s1=sxx-x0sx,s2=syy-y0sy,s3=sxy-x0sy;sx为对x轴的面积矩；sy为对y轴的面积矩；sxx为对x轴的面积惯性矩；syy为对y轴的面积惯性矩；sxy为对x和y轴的面积惯性矩。

对于块体M有

s=a2,

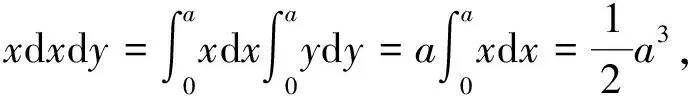
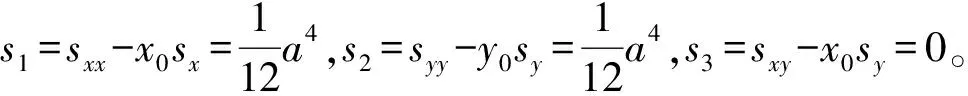
这里只对静力条件下的惯性子矩阵进行推导。即每个时步的开始速度为0，故V0=0，0表示零矩阵，公式(8)为“0”，该处0也表示零矩阵。故经计算，只形成加到K11的惯性子矩阵，其惯性子矩阵为

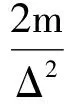
(10)

3.2.2 弹性子矩阵

块体i的弹性应力所产生的应变能为

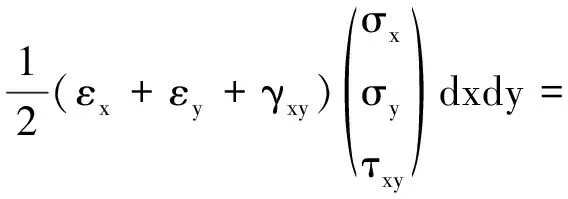
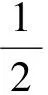
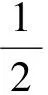
(11)

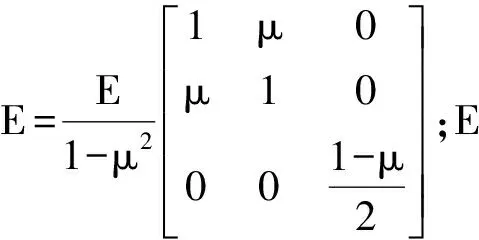
根据总势能最小，对∏e求导，可得到相应的弹性子矩阵为

sEi→Kii。

(12)

对于块体M，形成的弹性子矩阵为

(13)

3.2.3 弹簧子矩阵

由于弹簧子矩阵推导很复杂，涉及的变量很多，这里就没有写出详细推导过程。针对该块体接触模型，直接引用文献[1]中的公式：

(14)

(15)

(16)

第2个弹簧矩阵(x1=a，y1=0)为

(17)

3.2.4 载荷子矩阵

假设荷载是分布在从点(x1,y1)到点(x2,y2)的线段上，受荷线段的直线方程为

(18)

(19)

此处荷载沿作用线变化。线荷载(Fx(k),Fy(k))的势能为

(20)

计算∏l的导数，即求势能∏l的极小值：

r=1,…,6 。

(21)

其中

(22)

对于块体M，Fx=0，Fy=-σ，(x1,y1)=(0,a)，(x2,y2)=(a,a)，l=a。则加到F1的载荷子矩阵为

=

(23)

3.3 接触位移理论公式

对于静力问题，由式(10)、式(13)、式(16)和式(17)形成刚度系数子矩阵K11，式(23)形成F1，由总方程KD=F求解变形变量。经计算分析，最终得到3个方程：

经计算求解，获得接触部位的变形变量D1=(0,v1,0,εx1,εy1,0)T。各相关分量计算公式为

(24)

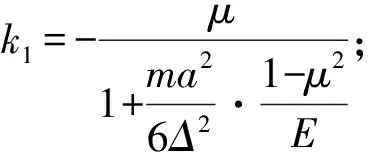
表2 p=1E下的接触位移

表3 p=10E下的接触位移

由式(24)可知，2块体的接触位移与块体的变形模量E、弹簧刚度p和时间步长Δ相关。在变形模量E和弹簧刚度p一定条件下，2块体的接触位移与时间步长直接有关。而且DDA中惯性力的引入直接与时间步长相关，因此，将惯性问题引入块体接触收敛求解的本质问题是通过调整时间步长，实现块体接触开-闭迭代收敛。

4 DDA块体接触力及位移理论解分析

取块体M边长a=1 m,重度为2.7 T/m3，均布荷载σ=2.7 T/m2。由公式(24)计算2接触弹簧处的变形变量。

4.1 接触力计算

取E=10 GPa，p=10E,不同时间步长下,法向接触力如表1所示。

表1 不同的时间步长下的法向接触力

由于块体M的外荷载σ=26.5 kN/m2，表1中法向接触力与外荷载的相对误差小于0.000 05%，则根据式(24)理论公式计算的法向接触力可认为是与外力平衡的。由此，接触部位满足力的平衡，该公式的正确性得到了验证。

4.2 接触位移理论解计算及分析

分别取不同的块体变形模量E、弹簧刚度p和时间步长Δ，由公式(1)计算块体M接触位移。经计算分析，2弹簧接触处的位移完全相同，现得到如表2至表4计算结果。

表4 p=100E下的接触位移

分析表2至表4，当块体变形模量E、弹簧刚度系数一定时，时间步长Δ越小，接触部位的侵入位移越小；当时间步长Δ、弹簧刚度系数一定时，块体变形模量E越大，接触部位的侵入位移越小；当块体变形模量E、时间步长Δ一定时，弹簧刚度系数越大，接触部位的侵入位移越小。

取E=10 GPa，p=10E, 接触部位的侵入位移随时间步长的关系曲线如图2所示。

图2 接触位移与时间步长的关系曲线

图2表明，在变形模量和弹簧刚度一定条件下，时间步长越小，接触部位的侵入位移越小。为了保证块体系统的开-闭迭代收敛，应合理地调整时间步长。

5 结 论

非连续变形分析是一种隐式求解的动力学计算方法，且采用在块体界面加减刚硬弹簧的方式来满足块体界面无张拉和无嵌入的接触准则。本文基于块体接触分析模型，推导了静力条件下块体接触位移理论公式，并通过接触力的计算验证了该公式的正确性。进而探讨了块体变形模量、弹簧刚度和时间步长与块体接触位移的相互关系，在变形模量和弹簧刚度一定条件下，2块体在接触部位的位移将直接与时间步长有关，时间步长越小，接触部位的侵入位移越小。该结论也证明了石根华博士在DDA计算中采用时间步长来调整和加快开-闭迭代收敛的策略是合理、高效的。而且，DDA中惯性力的引入直接与时间步相关，因此，将惯性问题引入块体接触收敛求解的本质问题是通过调整时间步长，实现块体接触开-闭迭代收敛。

参考文献：

[1] SHI Gen-hua. Discontinuous Deformation Analysis: A New Numerical Model for the Statics and Dynamics of Block System[D]. Berkeley: Department of Civil Engineering, University of California, 1988.

[2] 石根华. 数值流形方法与非连续变形分析[M]. 裴觉民，译. 北京：清华大学出版社, 1997. (SHI Gen-hua. Numerical Manifold Method and Discontinuous Deformation Analysis [M]. Translated by PEI Jue-min. Beijing: Tsinghua University Press, 1997.(in Chinese))

[3] MACLAUGHLIN M M, BERGER E A. A Decade of DDA Validation[C]∥Proceedings of the 6th International Conference on Analysis of Discontinuous Deformation, Norway, October 5-8, 2003:13-32.

[4] OHNISHI Y, NISHIYAMA S, SAKAKI T,etal. The Application of DDA to Practical Rock Engineering Problems: Issues and Recent insights[C]∥Proceedings of the 7th International Conference on Analysis of Discontinuous Deformation, Hawaii, December 10-12, 2005: 277-287.

[5] WANG C Y, SHENG J, CHEN M H. Time Integration Theories for the DDA Method with Finite Element Meshes[C]∥Proceedings of the First International Forum on Discontinuous Deformation Analysis (DDA) and Simulations of Discontinuous Media, Albuquerque: TSI Press, June 12-14, 1996: 263-287.

[6] 邬爱清，丁秀丽，陈胜宏,等. DDA方法在复杂地质条件下地下厂房围岩变形与破坏特征分析中的应用研究[J]. 岩石力学与工程学报，2006,25(1):1-8. (WU Ai-qing, DING Xiu-li, CHEN Sheng-hong,etal. Researches on Deformation and Failure Characteristics of an Underground Powerhouse with Complicated Geological Conditions by DDA Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1):1-8.(in Chinese))

[7] MACLAUGHLIN M, SITAR N, DOOLIN D,etal. Investigation of Slope-stability Kinematics Using Discontinuous Deformation Analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(5): 753-762.

[8] HATZOR Y H, FEINTUCH A. The Validity of Dynamic Block Displacement Prediction Using DDA[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38: 599-606.

[9] 邬爱清. DDA方法块体稳定性验证及其在岩质边坡稳定性分析中的应用[J].岩石力学与工程学报，2008,27(4): 664-672. (WU Ai-qing. Validation for Rock Block Stability and Its Application to Rock Slope Stability Evaluation Using DDA Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 664-672.(in Chinese))

[10] 邱宽红，林绍忠，黄 斌. 基于DDA的膨胀土边坡破坏过程模拟[J]. 长江科学院院报，2009,26(11)：58-61. (QIU Kuan-hong, LIN Shao-zhong, HUANG Bin. Failure Simulation of Expansive Soil Slope Based on DDA [J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(11): 58-61. (in Chinese))

[11] 刘 军，李仲奎. 非连续变形分析方法中一些控制参数的设置[J]. 成都理工大学学报(自然科学版)，2004, 31(5):522-526.(LIU Jun, LI Zhong-kui. Setting Some Control Parameters in the Discontinuous Deformation Analysis Method[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2004, 31(5): 522-526.(in Chinese))