建基面与软弱结构面组合的抗滑稳定分析方法探讨

，

(1.中国水电顾问集团成都勘测设计研究院，成都 610072; 2.二滩水电开发有限责任公司， 成都 610051)

对于带部分建基面的大坝浅层和深层抗滑稳定计算问题，滑移模式较为复杂，常规规范方法不能完成计算，虽然也可用有限元等方法计算，但过于复杂和繁琐。本文在《混凝土重力坝设计规范》(SL219—2005)双滑面计算方法的基础上，推导了带建基面的复杂滑移通道的抗滑稳定计算方法，可解决工程中带部分建基面的大坝失稳滑移模式的抗滑稳定计算问题。

1 带部分建基面的深层抗滑稳定滑移模式

坝基深层抗滑稳定的滑移模式与特定结构面的分布有关。对图1所示的例题，f1错动带在坝基中部出露，且f1和f2错动带可形成滑移通道，所以ACDE可能成为其失稳滑移模式，该滑移通道上AC为建基面。图中①为虚拟滑块AC，②,③分别表示滑块BCD和BDE。

图1 建基面与特定结构面组合的滑移模式

对上述带部分建基面的深层抗滑稳定滑移模式，由于滑移通道的复杂性，无法直接利用重力坝设计规范方法进行抗滑稳定计算。本文将依照规范的刚体极限平衡原理，推导计算方法进行求解。

2 求解方法推导

对图1所示的滑移模式进行受力分析，如图2所示。其中建基面以上的竖向荷载和水平荷载分摊到AC，CB面；AC，CD，DE均受到扬压力U、基岩反作用力N和T；滑块BCD和滑块BDE受到自重G；滑块间BD面抗力R2及水平扬压力UP。

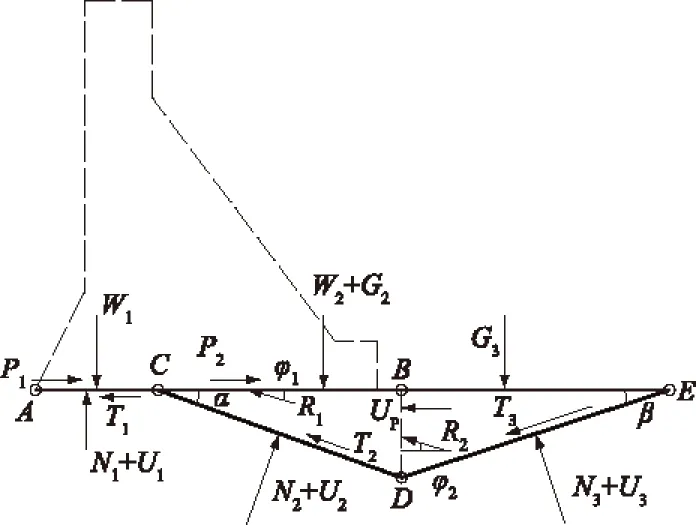
图2 建基面与特定结构面组合的受力分析

值得说明的是，AC，CB面上所受的大坝竖向和水平荷载，可以采用应力分摊的方式求解。根据相关文献[1]，坝基面竖向应力σy呈线性分布，水平应力τ呈抛物线分布，按照《混凝土重力坝设计规范》(SL219—2005)附录C可分别求出应力分布主要参数。

按照潘家铮的“最大最小原理”[2]，抗滑稳定各滑面的抗力可通过自行调整，以发挥最大的抗滑能力。因此，在BC界面上增加一个抗力R1，该抗力与BD界面上R2一样，起调整各滑移面安全系数的作用，使得整体滑移模式抗滑能力最强。

按照上述受力分析，基于刚体极限平衡原理，可以列出沿ACDE通道上各滑面抗滑稳定的求解公式：

(1)

K2={[(W2+G2)cosα-P2sinα+R1sin(φ1-α)-

G2)sinα+P2cosα+R1cos(φ1-α)-

R2cos(φ2-α)-Upcosα],

(2)

K3={[G2cosβ+R2sin(φ2+β)-

R2cos(φ2+β)+Upcosβ]。

(3)

采用等安全系数的概念，有

K=K1=K2=K3。

(4)

将式(4)代入式(1)至式(3)后，共有3个未知变量R1，R2，K，方程可解。上述方程为非线性方程组，其特点与文献[3]相同，可采用迭代法求解。

3 例题试算

对图1例题进行试算，其滑移通道计算参数见表1，大坝混凝土重度取24 kN/m3，基岩重度取26 kN/m3，主排水管x位置距坝踵10 m，扬压力折减系数为0.25。

表1 例题滑移通道计算参数

进行正常工况抗滑稳定计算，建基面以上竖向荷载70 905.39kN，水平荷载28 282.08kN，并进行荷载分摊(见表2)，计算中φi均取0。

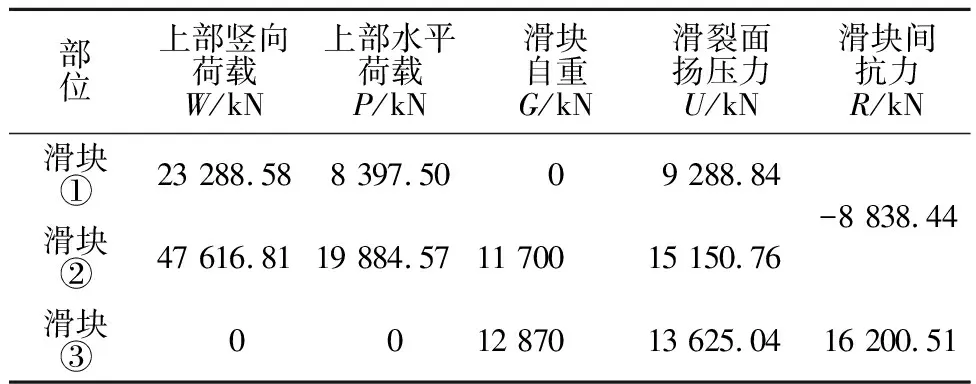
表2 例题抗滑稳定计算结果

注：水平力向下游为正，竖向力向下为正;安全系数K=2.715。

从表1和表2可知，由于f1和f2错动带形成的滑移通道参数较低，对抗滑稳定极为不利，导致整体安全系数为K=2.715,小于规范要求的3.0。值得说明的是，由于AC为坝体与基岩接触面，参数较高，能承受较大的抗滑作用，在各滑面的抗力自行调整后，AC面将产生较大的抗滑力(向上游)，并通过大坝传递给滑块体BCD，因此R1为BC面上的拉力(表2中R1表现为负值)。

4 工程验证

向家坝为金沙江梯级开发中下游的大型水电站，受地质构造的影响，立煤湾漆状挠曲带从坝址西北角延伸到东南角，与坝轴线呈斜交状态。坝基岩体完整性差，存在2条一级和10余条二级中缓倾向下游且贯通性好的软弱夹层，构成了大坝深层滑动的控制性结构面[5]。

图3为向家坝泄12坝段剖面图。从图中可以看出，坝基分布有T32-3,T32-5等软弱夹层带，其中T32-5在坝基中部出露。在水平荷载作用下，大坝可沿建基面、T32-5滑动，从下游基岩抗力体缓倾上游的结构面和岩桥组合剪出面滑出。

图3 向家坝泄12坝段剖面图

对泄12坝段上述滑移模式采用本文方法进行验算，计算参数和计算成果见表3、表4。

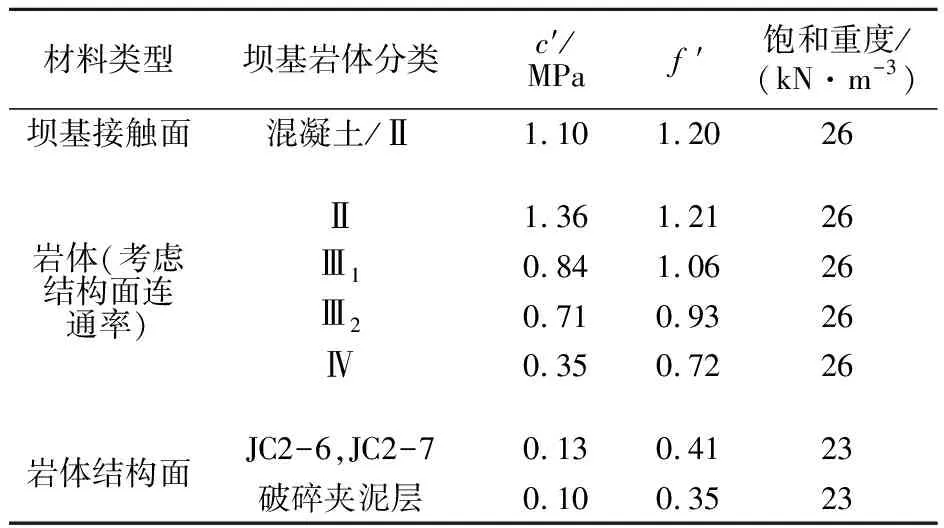
表3 向家坝抗滑稳定计算参数

注：计算中T32-5顶面取破碎夹泥层参数。

表4 向家坝泄12坝段抗滑稳定计算结果对比

为对比，表4中列出了Sarma法[5]和有限元法[6]的相关计算成果，其中有限元法采用材料抗剪强度折减法，坝基逼近临界破坏状态时的折减系数为3.6。

需要说明的是，本文方法计算结果与Sarma法计算结果有差异，可能原因是：①计算原理不一样。Sarma法以滑面及各条块侧面均达到极限平衡状态为计算原理，与本文基于简化毕肖普法推导的计算方法稍有不同，本文方法偏于保守，安全系数相对更低；②荷载施加有差异。Sarma法计算时将大坝自重荷载进行条分加在坝基滑块上，相对粗糙；本文按应力分布原理分摊建基面荷载，相比之下更符合实际受力情况。通过分析可知，Sarma法加在坝基面上的大坝竖向荷载要多一些，而建基面抗剪断参数较高，对抗滑稳定较为有利，也是导致计算结果差异的主要原因。

5 结 语

对于建基面与特定结构面一起构成复杂滑移模式的深层抗滑稳定问题，本文在重力坝设计规范方法的基础上，根据等安全系数方法的原理推导了复杂滑移模式的求解方法，该方法采用应力分摊的方式将坝体荷载分解到各滑块，并基于刚体极限平衡原理求解滑移通道整体安全系数。本文方法的求解假定与重力坝设计规范采用的简化毕肖普法一致，符合水电水利工程的设计要求。

通过例题试算及工程验算，本文方法计算结果与Sarma法及有限元法结论基本一致，证明了本文方法的可行性。

参考文献：

[1] 祁庆和，水工建筑物(第三版)[M].北京：中国水利水电出版社，1997：60-62.(QI Qing-he. Hydraulic Structures(Third Edition)[M]. Beijing: China Water Power Press, 1997: 60-62.(in Chinese))

[2] 潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京：水利出版社，1980.(PAN Jia-zheng. Slide-resistant Stability and Landslide Analysis of Structures[M]. Beijing: Water Power Press, 1980.(in Chinese))

[3] 彭文明.多滑动面深层抗滑稳定求解方法探讨[J].水电站设计，2009, (3):1-3.(PENG Wen-ming. Study on Stability against Deep Slide with Multiple Slip Planes[J]. Design of Hydroelectric Power Station, 2009, (3): 1-3.(in Chinese))

[4] 任青文.拱坝坝肩稳定分析中非线性方程组的线性化解法[J].河海大学学报，1991，19(3)：120-124.(REN Qing-wen. Linearized Solution to the Nonlinear Equations in Stability Analysis for Arch Dam Abutement[J]. Journal of Hohai University, 1991，19(3)：120-124.(in Chinese))

[5] 周建平，钮新强，贾金生.重力坝设计二十年[M].北京：中国水利水电出版社，2008.(ZHOU Jian-ping, NIU Xin-qiang, JIA Jin-sheng. Two Decades of Gravity Dam Design[M]. Beijing: China Water Power Press, 2008.(in Chinese))

[6] 于 沭.向家坝水电站两个坝段坝基深层抗滑稳定分析[D].北京：中国地质大学，2007.(YU Shu. Deep Slide-resistant Stability of the Foundation of Two Dam Blocks in Xiangjiaba Dam[D]. Beijing: China University of Geosciences, 2007.(in Chinese))