考虑雾化雨条件下边坡的稳定性分析

，

(1.四川理工学院 建筑工程学院，四川 自贡 643000；2.西南交通大学 岩土工程系，成都 610031)

1 研究思路

国内外在地下水对边坡的作用方面作了大量的研究[1]，主要有：Picarelli等[2]对地下水作用下的边坡破坏机理进行了研究；Uchida等[3]对地下水渗流的程度、范围和速率进行了分析；李文秀等[4]采用Fuzzy数学理论中的Fuzzy测度理论，对岩质边坡在地下水影响下的总体稳定性进行了预测；吴海艳等[5]将流固耦合理论引入边坡的稳定分析，提出了以位移和速率为标准的边坡稳定性评价方法。同时，降雨入渗导致边坡滑动是一个极其复杂的物理力学过程，它涉及坡面径流、渗流与应力场耦合等问题[6-8]。总结前人的研究成果不难发现，虽然有关地下水与边坡稳定性的关系方面取得了一定研究成果，但仍有2个基本问题需要解决：地下水作用下的边坡稳定性评价方法及采用排水或加固措施后的边坡稳定性评价方法。地下水作为一种敏感性因素，需要要用动态的观点来研究边坡体内的地下水作用，这样才会更符合实际情况。

本文采用渗流理论，对雾化雨渗透作用下的锦屏水电站边坡的稳定性进行动态的评价。实际上，土的力学参数具有一定的随机性及变异性，将土、荷载及计算模式都视为确定性的对象，得出的安全系数并不能全面客观地反映边坡的真实安全程度，可靠性分析是将有关参数作为非确定性对象，利用概率论及数理统计的方法研究边坡的稳定性，可以有效地解决上述问题。在此背景下，分析雾化雨入渗条件下边坡失稳机理与加固，探讨变化规律，具有其理论和现实意义。

雾化雨入渗会降低岩石或土体的抗剪强度，使得边坡地下水位和孔隙水压力升高，因此需要对雾化雨入渗对边坡稳定性影响进行研究分析。在锦屏水电站滑坡现场勘察、测试及室内试验的基础上，结合数值分析软件SLIDE，通过模型边界条件的改变来控制降雨入渗深度，并用渗流理论研究边坡在不同降雨入渗深度下的水压力和安全系数等方面的变化规律，并从多角度探讨边坡的稳定性评价方法。

同时，有自由面的渗流计算是一个难点[8]，其主要方法主要分为变动网格法和固定网格法，本文采用固定网格法，并考虑非饱和土的渗透性影响。

2 工程地质条件及边坡稳定性分析方法

2.1 工程地质条件

通过锦屏水电站泄洪雾化区左岸坝桩号1+340至1+580 m段覆盖层的地质调查和补充坑探揭示条件的编录分析，该边坡覆盖层工程地质条件如下。

该段覆盖层的分布范围：位于泄洪洞出口对岸山坡上，分布在高程1 710～1 860 m范围内，顺河向厚度分布不均匀，坑探揭示在坝桩号1+400 m剖面上垂直厚度一般为5～6 m，在坝桩号1+450 m剖面上垂直厚度一般为3～4 m，在坝桩号1+500 m剖面上垂直厚度一般为4～5 m；随高程降低，覆盖层厚度也逐渐变薄，最厚部位位于动防护网上下20 m高差范围内。

物质组成及结构特征：该段覆盖层为第四系坡残积体(Qdl及Qel)，其物质组成为灰褐色含块状碎石土，结构中密，块状碎石占40%～60%，块径一般5～20 cm，块状碎石岩性主要为板岩及少量砂岩，充填物为粉质黏土。表层植物根系发育。下伏基岩为砂板岩和大理岩，岩层倾坡内，产状NE30°～40°/NW30°～40°。岩体风化卸荷强烈，裂隙发育，基岩面起伏不平。

根据工程地质条件勘察及反演分析，雨水作用下土体的主要物理力学参数见表1。经室内实验测定，碎石土排除雨水后其抗剪强度的c值不变，内摩擦角提高2°。

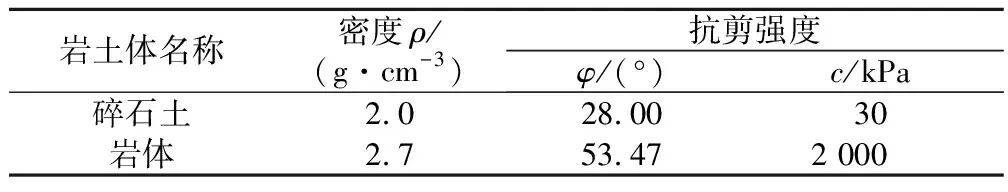
表1 岩土体主要物理力学参数建议值表

2.2 滑面确定

边坡的稳定性评价除了安全系数的计算外，在很多情况下滑动面并不确定，还需要对潜在危险滑动面进行搜索。在一般的滑坡中，可以通过钻孔和现场勘察的土层详细资料确定大致的滑动面位置。但对于本工程边坡，由于基岩及覆盖层的界面很长，地质条件复杂多变，且大都为局部破坏或崩塌，无法详尽地知道各处滑动面的位置。在这种情况下，如何对其最危险滑动面进行搜索，从而提出合理、有效的治理方案，成为评价边坡稳定的一个首要问题。因此需要采用经典极限平衡法、简化毕肖普法、简布法、修正的简布法、斯宾塞法、Fellenius法拟定多种滑体形态确定多组滑裂面进行稳定分析，比较不同滑动面条件下的稳定状况，从而确定最危险滑动面的位置。

2.3 工况的考虑

影响边坡稳定性的作用可以分为自重作用、地下水作用、地震力作用和加固力作用，各种作用包括不同的基本组合和偶然组合。考虑不同的组合则形成了不同的边坡设计状况。根据《水电边坡工程设计规范(征求意见稿)》，并结合本工程的实际情况，分析了边坡在开挖后的稳定性，共设计了2种不同的计算工况，即：

(1) 天然状况，即只考虑自重；

(2) 自重+降雨；采用边坡体孔隙水压力系数为0.1进行计算。

3 渗流稳定性分析

3.1 计算模型

选取坝桩号1+650 m典型剖面进行了泄洪雾化雨作用下的渗流分析，计算模型如图1所示，其中物质1为基岩，物质2为碎石土，碎石土的本构模型采用Mohr-Coulomb模型，碎石土分布在高程1 705～1 825 m范围之内，基岩与碎石土接触面长度为178.05 m；由潜在滑体碎石土高程1 825 m向左取45 m、高程1 705 m向下取65 m为有限元的计算分析边界，不考虑边界的位移和渗流，即边界位移为0，渗透系数为0。

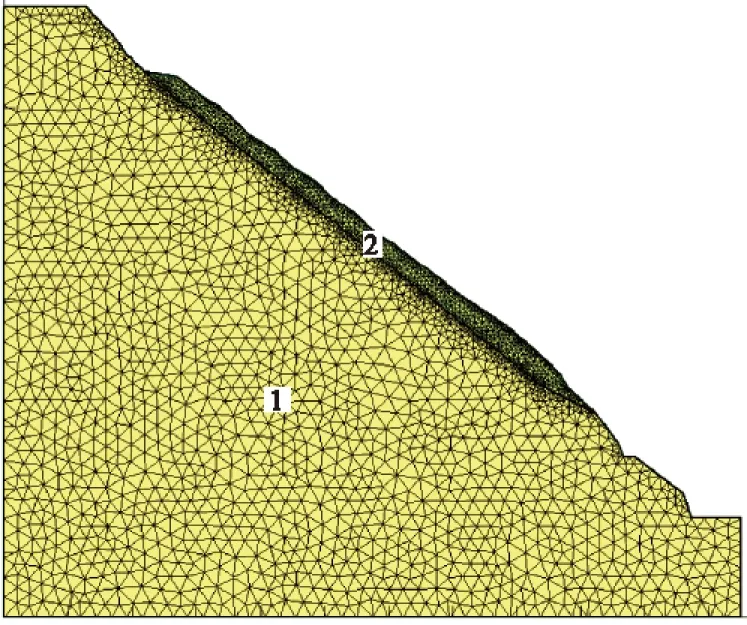
图1 渗流计算模型

对于不可压缩流体，根据水流的连续性条件和达西定律，当渗透系数kx=kz=k时，测管水头h满足如下的微分方程：

(1)

其中，h=z+u/rw，为重力势和压力势之和。

根据h的泛涵及变分，渗流能I(h)为

(2)

参考《泄洪雾化区左岸Ⅳ,Ⅵ号山梁及右岸猴子坡稳定分析及加固设计研究专题报告》，按V级岩体较松弛的岩块岩屑型确定覆盖层的饱和渗透系数为0.72 m/h。坝1+650 m处的雾化雨强度如表2所示。

边界条件：按照雾化雨强度设置覆盖层表面渗流边界为单位流量边界，1 705 m高程以下为总水头边界(H=0)，通过设置极低的饱和渗透系数(K=2.80×10-8cm/s)以确保下部基岩为弱透水边界。

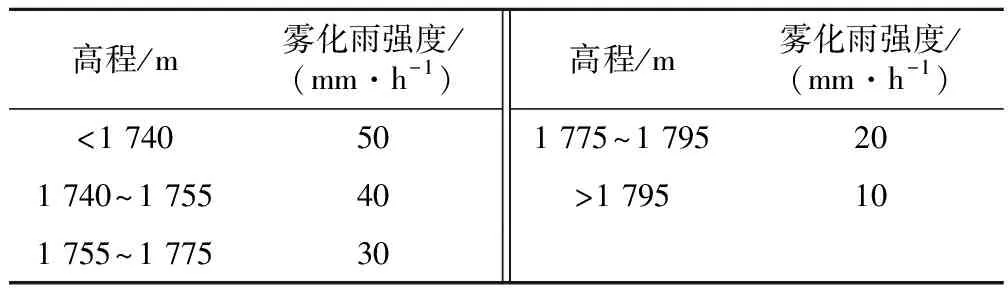
表2 雾化雨强度随高程变化情况表

其中：高程1 705 m以下为泄水区。

雾化雨渗流计算结束后，将水压力计算结果耦合于二维刚体极限平衡法中，核算下图2所示的各种潜在可能的滑面并计算滑体的安全系数。边坡潜在可能的滑坡破坏模式为：覆盖层发生沿碎石土与基岩接触面的滑坡；覆盖层边坡可能发生内部的折线形或圆弧形滑坡。经过滑面搜索及安全系数的比较，滑面沿覆盖层内部折线形滑坡的安全系数最小(图3)，限于篇幅本文仅给出折线形滑坡的安全系数分析结果。

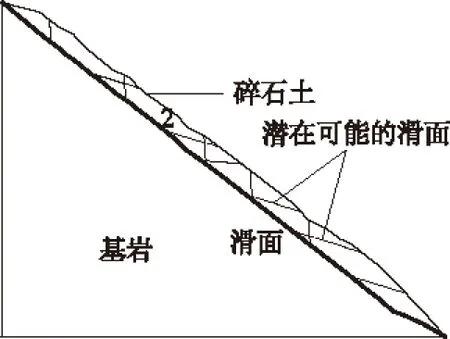
图2 各种潜在可能的滑面

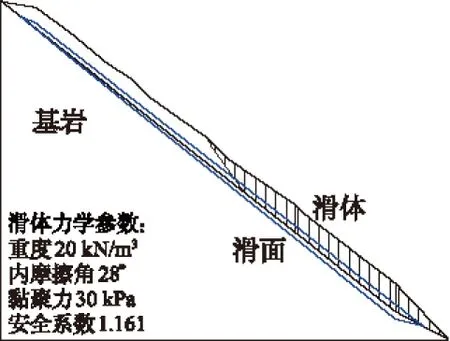
图3 雾化作用前边坡稳定性

3.2 计算结果

本文对坡体在雾化作用前和雾化雨作用1～5 d的水压力及坡体稳定性进行了计算分析，限于篇幅，本文给出了坡体在雾化雨作用1,2及5 d后的水压力等值线及坡体稳定性计算结果图(图4，图5)。图3所示的滑体为稳定性计算结果所拟定的最危险滑块，滑面为穿过覆盖层边坡内部的折线形滑面，滑面处基岩与碎石土接触面长度为81.72 m，分布在高程1 705～1 752.50 m范围之内，折线的起点位于高程1 705 m、顶点位于碎石土地表面高程1 771 m处。

图4 雾化雨作用后水压力等值线

图5 雾化雨作用后稳定性计算成果

图3至图5的计算结果表明：在雾化作用前，边坡的安全系数为1.161，坡体稳定性较好。雾化雨作用1 d后，坡体内水位线约位于坡体下部1/3处，边坡安全系数为1.069，相当于自然边坡暴雨工况(降雨量约720 mm)的稳定性状态。雾化雨作用2 d后，坡体下部水位线接近地表，坡体上部水位线位于坡体1/2高度处，边坡安全系数为0.979，稳定性低于临界状态，边坡有失稳可能。雾化雨作用3 d后，坡体下部水位线完全为地表面，坡体上部水位线位于坡体1/2高度以上，边坡稳定性较雾化2 d略有下降，为0.900，低于设计安全系数。上述结果表明，覆盖层边坡的稳定性仅取决于下部坡体，由于雾化3 d后，坡体下部已达到完全饱和状态，持续的雾化作用对坡体下部地下水位的改变不大，形成了稳定水流，因此边坡的安全系数也没有太大变化，如雾化5 d后，边坡的安全系数为0.851。

3.3 排水措施及支护力对边坡稳定性的影响分析

稳定性计算表明，工程边坡最危险的破坏模式是坝桩号1+650 m工程地质剖面的“上部覆盖层边坡内部折线形滑动破坏”，考虑到雾化雨作用范围的破坏机理是覆盖层下部首先启动的牵引式滑移破坏，因此需要对下部坡体加强支护。以坝桩号1+650 m工程地质剖面为反算剖面，以最危险破坏模式求算支护力，按照自重工况安全系数大于1.15，暴雨工况安全系数大于1.05为目标反算得到支护力，其他剖面安全系数自动满足要求。在最危险的破坏模式下，反算支护力为585 kN/m，边坡稳定性计算成果如表3所示(c=30 kPa，φ=28°)。

当工程中考虑排水措施和坡面防水措施，雾化雨能够得到有效疏干和减少入渗，则覆盖层坡体的抗剪强度能够得到提高，经室内实验测定，其内摩擦角提高2°，由此计算边坡的支护力为325 kN/m，在最危险的破坏模式下，边坡稳定性计算成果如表3所示(c=30 kPa，φ=30°)。

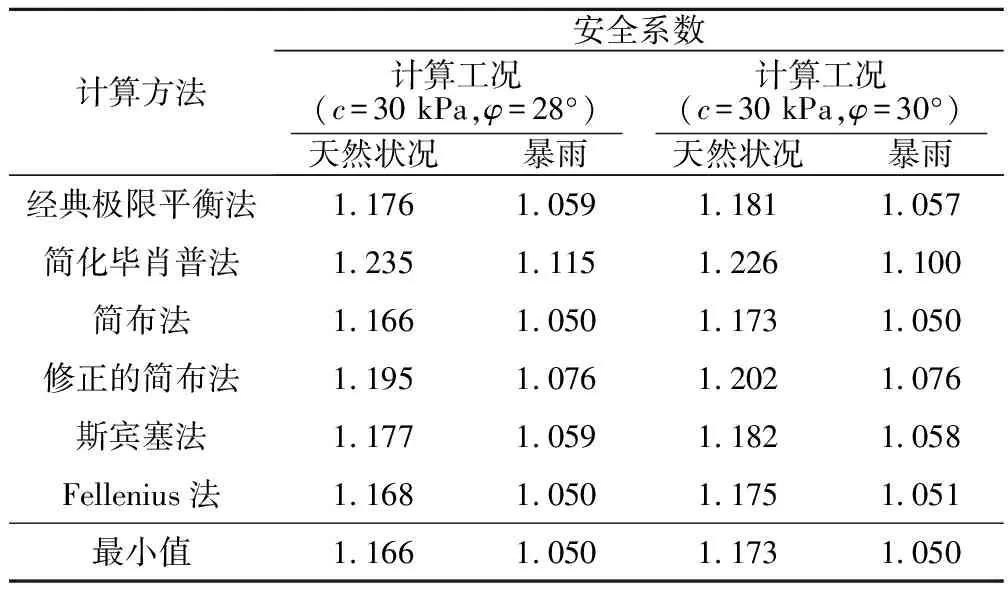
表3 覆盖层边坡的稳定性分析

上述计算成果表明，雾化雨是该处边坡稳定性的主要影响因素，除对边坡加强支护外，坡体内排水也是减小雾化雨影响、提高边坡稳定性的有力措施，以下分析了排水措施对边坡稳定性的影响。

以渗流计算模型为原型，由于计算模型为二维模型，采用排水量等效原则布置排水孔(设计采用间排距3 m布置排水孔，二维计算中采用上下排距10 m布置排水孔)。排水孔处的水力边界为水头边界(H=0)，以雾化雨作用5 d后的坡体稳定性进行分析。计算结果表明，由于布置了排水孔，坡体内仅排水孔之间的局部坡体部位有地下水存在，坡体内地下水没有连接成统一的水位。降雨5 d后，坡体达到了稳定渗流阶段，潜在失稳范围较未设置排水孔时有一定变化，相应的边坡安全系数为1.092，与前述计算结果比较可知，设置了排水孔后，即使是在长时间的雾化雨作用下，边坡的稳定性也较未设置排水孔时的边坡安全系数0.851要高。

3.4 土性参数的概率特性对边坡稳定性的影响分析

考虑到进行边坡稳定性分析时，传统的安全系数已经不能很准确地表达边坡发生破坏的概率，且未考虑到各主要参数的变异性对边坡稳定性的影响[9]，因此，在采用传统的安全系数法分析上述覆盖层边坡的稳定性分析后，还需采用可靠性设计方法对边坡进行稳定性分析，即结合经典极限平衡法、简化毕肖普法、简布法、修正的简布法、斯宾塞法、Fellenius法和Monte-Carlo数值模拟方法，运用土性参数的概率特性对边坡稳定性的影响[10-15]，并对2种方法的分析结果进行比较分析。

对于边坡的稳定性问题，可根据岩土体结构特点、破坏机理等，建立如下的状态函数[15]:

K=F(x1,x2,…,xm) 。

(3)

式中：xi=(1,2，…，m)代表随机变量，它们具有一定的分布特征(这些因素一般服从正态或对数正态分布)，其统计值己知。

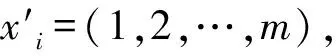
T=T1+T2+…+TN;

(4)

(5)

设在N次试验中， 安全系数K≤1的次数为numfailed，则边坡的破坏概率Pf为

(6)

当边坡的安全系数服从正态分布时，可靠指标β为

(7)

式中：μFS为安全系数平均值；σFS为安全系数标准差。

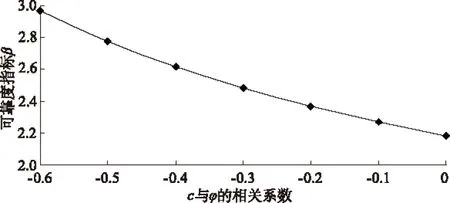
图6 土性参数c与φ值的相关系数r对可靠度指标的影响

分析结果表明：黏聚力变异系数δc、内摩擦角变异系数δφ及容重变异系数δγ的变化对边坡安全系数均值μFs的影响较小(表4)，但对边坡可靠度指标β的影响极为显现，可靠度指标β分别随着δc，δφ，δγ的增大而逐渐减小，其中黏聚力变异系数δc及内摩擦角变异系数δφ对边坡可靠度指标β的影响最为显著，容重变异系数δγ的变化对边坡可靠度指标β的影响小了许多，当δc，δφ，δγ分别增加50%，其它随机变量值不变时，可靠度指标β分别减少20.03%，21.96%，3.03%；土体抗剪强度参数c与φ值的互相关性也会对边坡稳定性评价产生较大影响(图6)，随着抗剪强度指标c与φ之间的负相关性的增强，可靠度指标β相应增大。因此采用固定的土性参数来计算边坡的稳定性不能全面地评价边坡的稳定性，而土体抗剪强度参数c,φ的变异性及其相关性是影响边坡可靠指标的一个极其重要的因素。

4 结 论

二维稳定性计算结果表明：正常状态下，覆盖层边坡的稳定性较好，自重工况下安全系数可达1.166左右，暴雨工况为1.05左右。但是，在泄洪雾化条件下，由于雾化降雨对覆盖层的降雨入渗作用，土体物理力学性状、土体与基岩接触面力学参数的恶化，该段覆盖层稳定性将变差。在暴雨工况下，边坡安全系数接近1.0，在长期的雾化雨作用下，边坡的安全系数最低为0.851。加之由于施工扰动，边坡的稳定性会进一步降低，可能发生土体滑坡。因此，需及时支护，以防止发生覆盖层土体滑动破坏。

采用排水、喷锚支护和下部锚索加固的综合处置措施。排水孔有利于边坡地下水的疏导，提高滑体抗剪强度，设置间排距3 m的排水孔后，在雾化雨长期作用下，边坡的安全系数可达到1.092(β值1.70)，高于未设置排水孔时的安全系数(0.851)；同时，喷锚支护可减少雾化雨入渗、增强滑体整体性，锚索可提高整个滑体的抗滑力，经综合比较分析，单位宽度的滑体锚索支护力可采用400 kN/m。

岩土体黏聚力变异系数δc及内摩擦角变异系数δφ对边坡的安全系数均值μFs的影响较小，而对边坡的可靠度指标β的影响极为显著，容重变异系数δγ的变化对边坡可靠度指标β的影响小了许多，当δc,δφ,δγ分别增加50%，其它随机变量值不变时，可靠度指标β分别减少20.03%,21.96%,3.03%；土体抗剪强度参数c,φ值的互相关性也会对边坡稳定性评价产生较大影响，随着抗剪强度指标c与φ之间的负相关性的增强，可靠指标相应增大。因此采用固定的土性参数来计算边坡的稳定性还不能全面地评价边坡的稳定性，土体抗剪强度参数c,φ的变异性及其相关性是影响边坡可靠度指标的一个极其重要的因素。

参考文献：

[1] 刘 燕, 王海平, 蒋永才. 长江三峡库区黄腊石边坡地下水作用规律与动态稳定性评价 [J].岩石力学与工程学报, 2005, 24(19): 3571-3576．(LIU Yan, WANG Hai-ping, JIANG Yong-cai. Groundwater Action Law and Evaluation on Dynamic Stability of Huanglashi Slope in Three Gorges Region[J]．Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3571-3576.(in Chinese))

[2] PICARELLI L,URCIUOLI G,RUSSO C.Effect of Ground-water Regime on the Behavior of Clayey Slopes[J]. Canadian Geotechnical Journal, 2004, 41(3): 467-484.

[3] UCHIDA T, ASANO Y, OHTE N,etal. Seepage Area and Rate of Bedrock Groundwater Discharge at a Granitic Unchanneled Hillslope[J]． Water Resources Research, 2003, 39(1): 10-18．

[4] 李文秀, 梁旭黎, 赵胜涛. 地下水影响下裂隙岩质边坡变形的Fuzzy测度分析[J].岩石力学与工程学报, 2005, 24(2): 302-306. (LI Wen-xiu, LIANG Xu-li, ZHAO Sheng-tao. Fuzzy Measure Analysis for Displacements and Deformations of Jointed Rock Slope under Influence of Groundwater[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 302-306 . (in Chinese))

[5] 吴海艳, 郭抗美, 王 超. 降雨入渗对黄土边坡破坏面的形成及滑动机理研究[J]. 路基工程,2011, 5(2): 146-149. (WU Hai-yan, GUO Kang-mei, WANG Chao. Study on the Influence of Rainfall Infiltration for Loess Slope Failure and the Mechanism of Sliding[J]. Subgrade Engineering, 2011, 5(2): 146-149.(in Chinese))

[6] 田东方, 刘德富, 王世梅. 土质边坡非饱和渗流场与应力场耦合数值分析[J].岩土力学,2009, 30(3): 810-814 . (TIAN Dong-fang, LIU De-fu, WANG Shi-mei. Coupling Numerical Analysis of Unsaturated Seepage and Stress Fields for Soil Slope[J]. Rock and Soil Mechanics, 2009, 30(3): 810-814. (in Chinese))

[7] 朱泽勋, 吴 莉. 基于SLIDE的某尾矿库边坡稳定性分析[J]. 采矿技术, 2011, 11(6)：49-128. (ZHU Ze-xun, WU Li. Slope Stability Analysis of a Mining Region Based on SLIDE[J]. Mining Technology, 2011, 11(6): 49-128. (in Chinese))

[8] 介玉新. 引用Monte Carlo法的自由面渗流分析[J]. 清华大学学报( 自然科学版), 2009, 49 (12): 1944-1947. (JIE Yu-xin. Seepage Analysis with Free Surface Using a Monte Carlo Model[J]. Chinese Journal of Tsinghua University( Natural Science) , 2009, 49 (12): 1944-1947. (in Chinese))

[9] 罗书学. 桩基概率极限状态法研究和工程应用[D]. 成都：西南交通大学, 2000. (LUO Shu-xue. Research and Engineering Application of Probability Limit State Design Method for Pile Foundation[D]. Chengdu: Southwest Jiaotong University, 2000. (in Chinese))

[10] 赵寿刚, 兰 雁, 沈细中. 蒙特卡罗法在土质边坡可靠性分析中的应用[J].人民黄河,2006, 28(5): 65-73. (ZHAO Shou-gang, LAN Yan, SHEN Xi-zhong. Application of Monte Carlo Method to the Reliability Analysis for Soil Slope[J]. Yellow River, 2006, 28(5): 65-73. (in Chinese))

[11] 陈菊香, 朱大勇, 卓建平,等. 基于Monte-Carlo法的土坡抗震可靠度分析[J]. 地下空间与工程学报,2005,5(5):884-892. (CHEN Ju-xiang ZHU Da-yong, ZHUO Jian-ping,etal. Reliability Study on Earth Slopes under Earthquake Based on Monte-Carlo Method[J]. Chinese Journal of Underground Space and Engineering, 2005, 5(5): 884-892. (in Chinese))

[12] 范明桥, 盛金保. 土强度指标c-φ的互相关性[J]. 岩土工程学报, 1997,19(7): 100-104. (FAN Ming-qiao, SHENG Jin-bao. The Cross Correlation of Soil Strength Indicatorsc-φ[J]. Chinese Journal of Geotechnical Engineering, 1997,19(7): 100-104. (in Chinese))

[13] 兰 雁, 赵寿刚, 沈细中,等. 土体强度指标的互相关性对堤防稳定性的影响[J].人民黄河, 2007, 29(3): 12-20. (LAN Yan, ZHAO Shou-gang, SHEN Xi-zhong,etal. Influence of Mutual Relativity of Intensity Index of Soil Mass to Stability of Embankments[J]. Yellow River, 2007, 29(3): 12-20. (in Chinese))

[14] 陈殿强. 评价碎石土抗剪强度的一种新方法[J]. 勘察科学技术, 1992, (4): 21-24. (CHEN Dian-qiang. A New Method to Assess the Shearing Resistance of Gravel Soils [J]. Site Investigation Science and Technology, 1992, (4): 21-24. (in Chinese))

[15] 李 晶．基于FLAC3D与Monte-Carlo法的边坡可靠性研究[D].兰州:兰州交通大学，2012. (LI Jing. Research of Slope Reliability Analysis Based on FLAC3Dand Monte Carlo Method[D]. Lanzhou: Lanzhou Jiaotong University, 2012. (in Chinese))