库水位变化和降雨作用下付家坪子高陡滑坡稳定性研究

,

(中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室, 武汉 430071)

1 研究背景

水库蓄水之后，根据水库运行调度方式，水位会有周期性的上升和下降，此时岸坡的地下水位也会随之发生变化，会同步产生相应的力学效应[1]：①岸坡被淹没的部分会有浮力作用，从而有效重力减少；②在水库水位骤降、库岸地下水响应不及时时，会在较大的水力梯度下形成动水压力，从而增大下滑力；③随着水位的升降变化，岩土体的饱和区与非饱和区也在不断变换，因而基质吸力和孔隙水压力也在不断地变化。降雨的入渗会引起地下水、坡体及滑带的物理力学性质发生改变，使岩土体的饱和度增加，同时降雨的入渗会降低岩土体的抗剪强度，抬高地下水位使得孔隙水压力升高，基质吸力则有所减小，另外长时间高强度的降雨会使得地下水位以上区域出现暂态饱和区[2]。我国西部正在或将要大力建设大中型水利水电工程，因此研究水库库岸滑坡在水库升降和降雨作用下的稳定性具有重要的理论意义和应用价值。

文献[3]分析了降雨和库水位联合作用下库岸边坡的暂态渗流场，并确定了不同降雨强度下滑坡的稳定性；文献[4]运用非饱和土渗流及抗剪强度理论，分析了降雨和库水位叠加作用对滑坡的渗流场和稳定性影响；文献[5]推导了库水位升降联合降雨作用下均质岸坡模型中浸润线的近似解析解；文献[6]建立了三峡库区千将坪滑坡的地质力学模型，指出水库蓄水是诱导该滑坡发生的主要因素；文献[7]通过建立水-气二相流模型，研究了库水位下降的岸坡非稳定渗流场。

上述研究为深入了解水库库岸滑坡在降雨及库水位变化作用下的稳定性具有重要意义，但所研究的滑坡坡度都比较缓，基本上没超过0.40，且滑坡体的后缘高程都不高。如文献[3]岸坡后缘高程约为250 m，平均坡度约为0.38；文献[4]滑坡的后缘高程约为320 m，平均坡度约为0.28；文献[5]模型的后缘高程约为400 m，平均坡度约为0.23；文献[6]滑坡的后缘高程为400 m，平均坡度约为0.30；文献[7]岸坡的顶部高程为185.3 m，坡比为1∶3。对于大型的高陡滑坡，并没有涉及。在我国西南，正在建设大型的水电工程，库区两岸高山峻岭，坡度比较陡峭，且雨水比较充沛，一旦发生滑坡，造成的灾害损失往往比之前研究的滑坡大得多。因此本文拟对库水位变化和降雨作用下付家坪子高陡滑坡的稳定性进行分析，希望对以后的工程有借鉴作用。

2 理论分析

2.1 饱和与非饱和渗流理论

随着水库水位的上涨和降落，滑坡体中的地下水位也会随之变化，因而在滑坡体中就会形成饱和区和非饱和区；当地下水位埋深较浅时，降雨的入渗也会改变地下水位，从而也会形成饱和区与非饱和区。饱和区的地下水与非饱和区的土壤水的运动是相互联系，这种由于水的运动导致岩土体状态的改变即为饱和与非饱和渗流问题。以压力水头h为控制方程的因变量，考虑渗透各向异性的饱和与非饱和渗流问题，可以得出二维饱和与非饱和渗流控制方程[8]：

(1)

式中：kx，ky分别为岩土体水平和垂直方向的渗透系数；ρw为水的密度；g为重力加速度；Q为施加的边界流量；mw为比水容重，定义为体积含水率θw对基质吸力偏导数的负值，即

(2)

mw也是土水特征曲线斜率的绝对值，因此在得到岩土体的土水特征曲线和渗透性函数曲线之后，并附加边界条件和初始条件，即可得到滑坡体的瞬态渗流场。

2.2 非饱和土的抗剪强度理论

在库水位变化和降雨条件下，滑坡体的饱和区与非饱和区在不断交替变化，因此要研究滑坡体的稳定性变化规律，采用非饱和土的抗剪强度理论比较合适。国内外就关于基质吸力对滑坡体稳定性的影响也做了一些研究[9-11]，认为基质吸力的贡献不可忽略。这里采用岩土界广泛认可的Fredlund的双应力变量公式[8]，即为

τ=c′+(σ-ua)tanφ′+(ua-uw)tanφb。

(3)

式中：c′,φ′为有效应力强度参数；σ为法向总应力；ua为孔隙气压力(本文认为孔隙气压力为大气压力)，即为0；uw为孔隙水压力； (ua-uw)为基质吸力；φb为基质吸力增加引起抗剪强度增加的曲线倾角(本文设定其为常量)。由上述公式可以看出，随着基质吸力压力的增减，抗剪强度也随之增减。

2.3 边坡稳定性分析的极限平衡法

边坡稳定性分析的方法目前主要有强度折减法和极限平衡法，在我国被广泛认可且拥有丰富的工程经验的是极限平衡法。传统的极限平衡法有瑞典圆弧法、Bishop法、剩余推力法和Morgenstern-Price法(简称M-P法)等，前3种方法虽然减少了计算量，但却大大简化了土条间的相互作用力，因此不能很好地反映各土条的实际受力情况。M-P法则是在滑裂面的形状、静力平衡以及多余未知数的迭代方面不做任何假定的方法，因而可以确定任意滑裂面的边坡稳定性，也能较好地反映出最危险滑面各土条间相互作用力的情况。本文拟采用M-P法来分析库岸滑坡的稳定性。

3 渗流模型的建立

3.1 工程概况

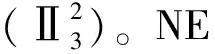
3.2 渗流计算模型

本文选择Ⅱ区滑坡段作为主滑剖面进行模拟，采用边坡稳定性分析软件SEEP/W 模拟滑坡在降雨和库水位变化条件下的暂态渗流场。根据滑面和岩性将滑坡体分为两层，库水位以上的表面坡作为入渗边界，库水位以下部分和边坡后缘作为定水头边界，底部也作为零流量边界。付家坪子主画面二维有限元网格剖分如图1所示。

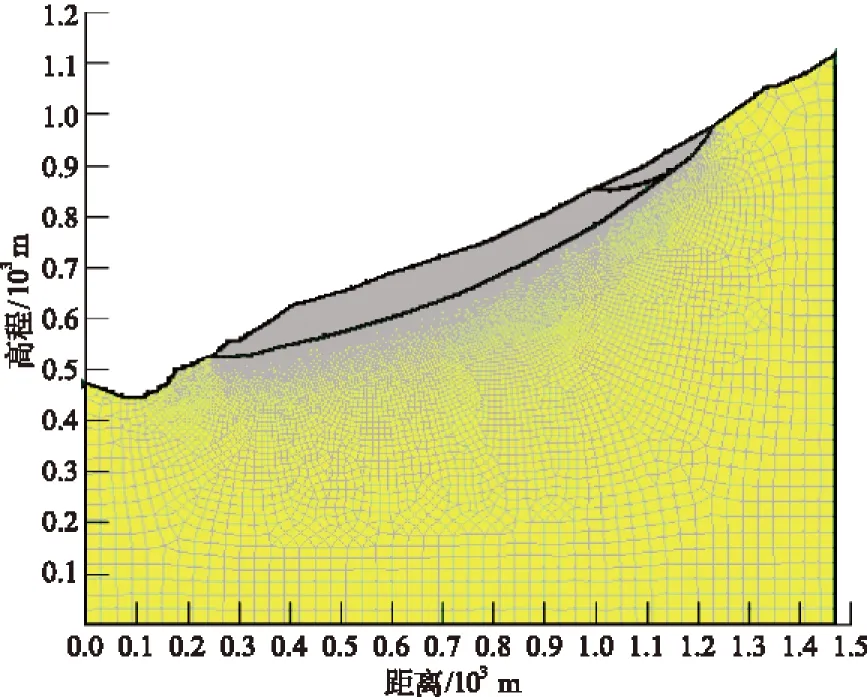
图1 付家坪子主滑面的二维有限元网格剖分图

3.3 计算参数

根据现场的原位试验和室内试验，滑坡体的上层土和滑床的饱和渗透系数分别为1.44×10-5m/s和5.787×10-7m/s。本文所用的土水特征曲线是由Van-Genuchten模型拟合而成，渗透性函数则是根据饱和渗透系数大小和土水特征曲线推导的。将SEEP/W 模拟出库水位变化和降雨引起滑坡体中的暂态孔隙水压力代入到SLOPE/W 中，根据M-P法计算出滑坡体各个工况下的安全系数。表1给出了滑坡土体的强度参数。

表1 滑坡体的强度参数

4 计算成果及分析

4.1 库水位变化对滑坡体稳定性的影响

4.1.1 库水位上升

为了研究库水位升速对滑坡稳定性的影响，根据水库调度曲线，本文设计了库水从560 m水位开始上升，升速分别为8,4,2 m/d 3种工况。图2表示库水位上升过程中安全系数的变化过程。

图2 库水位上升与安全系数的关系

由图2可知，库水位从560 m上升到600 m的过程中，安全系数一直是在增加。升速为8 m/d的安全系数增长速率最大，升速4 m/d次之，2 m/d的最小。说明了库水位上升越快，安全系数增长速率越大，安全系数也越大。升速越大，滑体内的地下水位线来不及随之上升，因此孔隙水压力和基质吸力的变化很小，而坡外的静水推力却在一直增加，从而使滑坡的安全系数增大；升速越小，滑坡体的浸润线会随水位的上升而上升，此时滑坡体的稳定性就由孔隙水压力、基质吸力和静水推力共同作用，但静水推力的影响最大，因而表现出了安全系数增大、增长速率却很小的规律。总的来看，3种工况下安全系数大小及其增长速率的差异均不大。

4.1.2 库水位下降

同样根据水库调度曲线，本文设计了库水从600 m水位开始下降，降速分别为0.667，0.364，0.267 m/d 3种工况。库水位下降过程中安全系数的变化过程如图3所示。

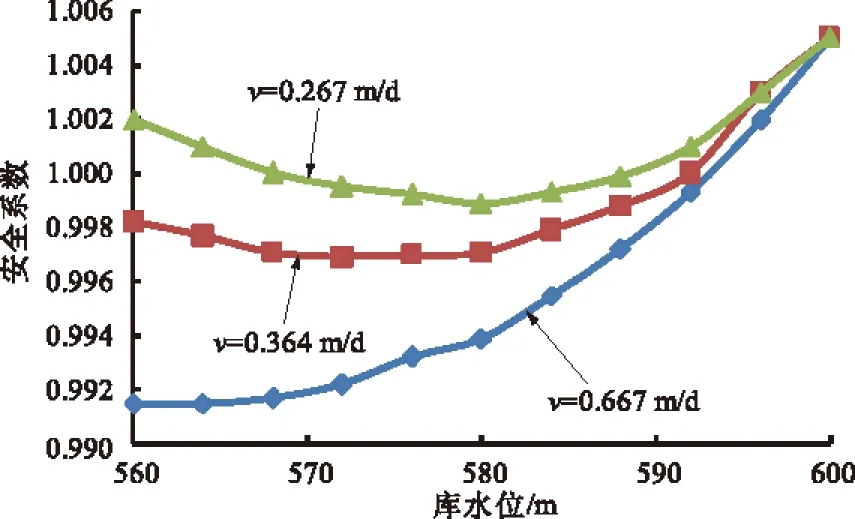
图3 库水位下降与安全系数的关系

由图3可知，滑坡体在3种工况下都有可能处于不稳定状态，尤其是降速v为0.667 m/d的工况；降速对滑坡稳定性的影响基本上呈抛物线变化，即安全系数先减小、后增加。水位在前期下降过程中，坡体中的地下水位来不及下降，而且会产生超孔隙水压力，随着时间的增加，坡体的地下水位也在下降，使坡体中的孔隙水压力减小，基质吸力增大，从而滑坡体的稳定性得到提高。此变化说明了在库水位下降过程中存在一个临界水位，如降速为0.667 m/d时，临界水位是560 m；当降速为0.364 m/d时，临界水位约为572 m；当降速为0.267 m/d时，临界水位在580 m左右。

4.2 降雨对滑坡体稳定性的影响

根据该地区的长年雨水统计资料，可知日最大降雨量为69.3 mm。为了研究不同库水位下的降雨强度对滑坡稳定性的影响，本文设计了天然水位、库水位为540，560 m；降雨强度分别为69.3mm/4 h,69.3 mm/6 h和69.3 mm/24 h。图4表示了不同水位下安全系数与时间的关系。图5给出了天然水位下持时为1.2 d不同降雨强度下有限元计算网格中x=320.21 m处孔隙水压力随埋深的变化。图6给出了天然水位下降雨强度为69.3 mm/24 h持时为5.4 d的降雨有限元计算网格中x=320.21 m处孔隙水压力随埋深的变化。

图4 不同库水位下安全系数与时间的关系

从图4可以看出，在不同库水位下，随着降雨强度的增大，安全系数减小速率越大；在一定的降雨强度下，安全系数随着时间的增加而减小；最大降雨强度与最小降雨强度对滑坡安全系数影响的差值均不超过0.01；在最大降雨强度下引起滑坡安全系数降低的幅度为：天然水位时，降低幅度为0.017；在540 m库水位时，降低幅度为0.015；在560 m库水位时，降低幅度为0.011。即安全系数的降低幅度都没有超过0.02，且随着库水位的升高，安全系数降低幅度减小。由图5可知，在相同持时下，随着降雨强度的增大，降雨入渗影响的深度也越大，边坡浅层岩土体的基质吸力也下降得越多。由图6可知，滑坡初始孔隙水压力分布于深度几乎成线性关系，随着降雨的发展，孔隙水压力的变化区域深度逐渐增大，变化区内基质吸力逐渐减小，可以看出降雨入渗是从坡面自上而下逐步发展的。

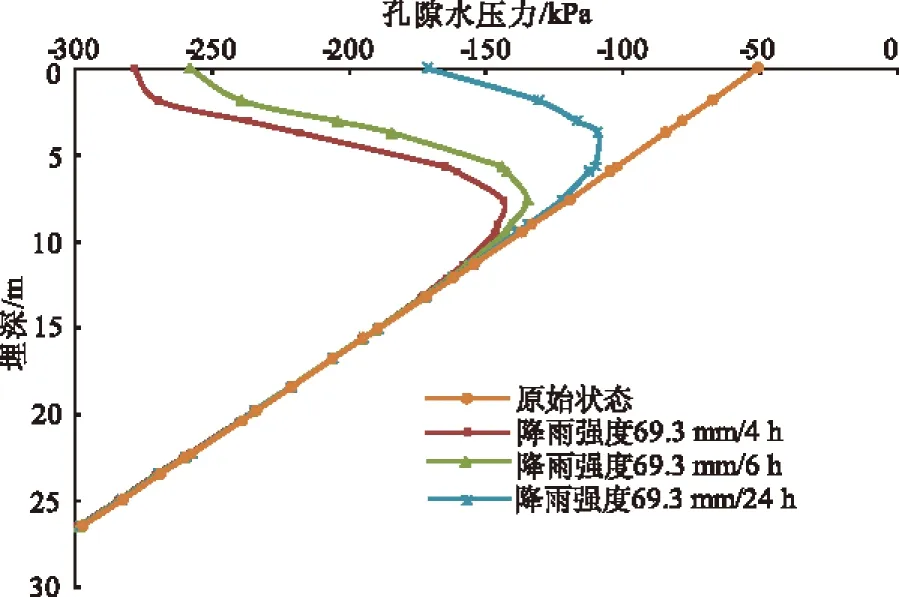
图5 不同降雨强度在天然水位下孔隙水压力随埋深的变化

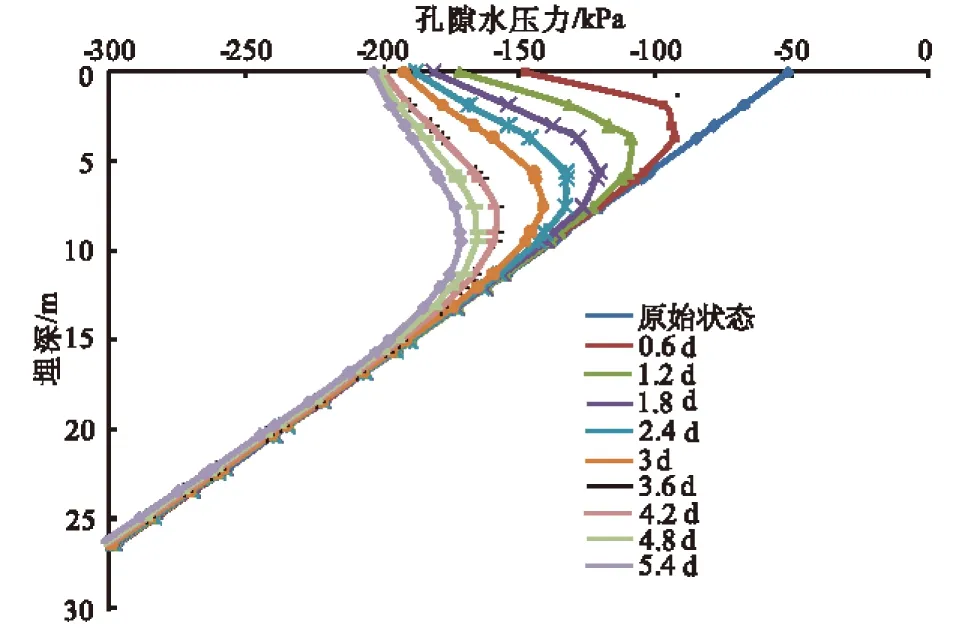
注：①降雨强度为69.3 mm/24 h;②在有限元计算网格中x=320.21 m处

4.3 库水位变化和降雨联合作用对滑坡体稳定性的影响

在库水位变化和降雨研究的基础上，对最不利条件进行组合，分析付家坪子滑坡在库水位变化和降雨联合作用下的稳定性。本文选择了一种最不利的工况：库水位从600 m降到560 m，降速为0.667 m/d；降雨强度为69.3 mm/4 h。为研究库水位下降与降雨在时间上的最不利组合方式，本文设计了降雨发生在最初和在最末2种方式。库水位下降和降雨联合作用下安全系数与时间的关系如图7所示。

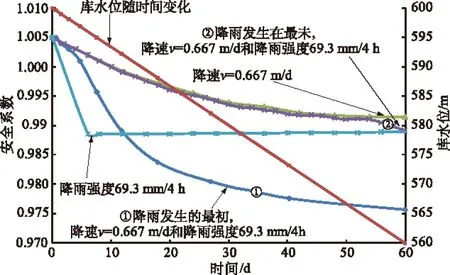
图7 库水位变化和降雨联合作用下安全系数与时间的关系

从图7可知，在库水位变化和降雨联合作用下，降雨发生在最初安全系数的减小速率在前6 d内与降雨单独作用下的基本相同，在后期则与库水位下降单独作用下的基本上相同，但安全系数下降幅度均比两者单独作用下的大，此时滑坡体处于最危险的状态；降雨发生在最末安全系数的减小速率基本上与库水位下降单独作用下的相同，只是在后期稍微有点下降，下降幅度却不大，在下降到560 m水位时，安全系数却与降雨单独作用的基本一致。说明了降雨发生在最初比发生在最末更危险，应该多注意。

5 结 论

(1) 库水位上升越快，滑坡安全系数的增长速率越大，安全系数也越大；在不同降速下，滑坡均处于不稳定状态，且降速对滑坡稳定性的影响基本上呈抛物线变化，即安全系数先减小，后增加，每个降速下均存在一个临界水位。

(2) 在一定的降雨强度下，安全系数随着时间的增加而减小，随着降雨强度的增大，安全系数减小速率越大；不同库水位下，最大降雨强度与最小降雨强度对滑坡安全系数影响的差值均不超过0.01，安全系数的降低幅度都不超过0.02，且随着库水位的升高，安全系数降低幅度减小。

(3) 在相同持时下，当降雨强度小于滑坡体的饱和渗透系数时，随着降雨强度的增大，边坡浅层岩土体的基质吸力下降得越多；随着降雨的发展，孔隙水压力的变化区域深度逐渐增大，变化区内基质吸力则逐渐减小。

(4) 在研究库水位下降与降雨在时间上的最不利组合方式时，发现降雨作用在最末对滑坡稳定性的影响比作用在最初要有利。

(5) 该滑坡只有在库水位上升过程中，才处于稳定状态，而在库水位下降、降雨以及库水位变化和降雨联合作用下稳定性都较差，但在所有工况下，安全系数的变化幅度均很小，最大的变化幅度也只为0.031。

参考文献：

[1] 吴争光. 库水位变化对库岸边坡稳定性影响研究[J]. 灾害与防治工程，2009，(1)：1-6.(WU Zheng-guang. The Influence of Water Level Fluctuation on Bank Slope Stability[J]. Disaster and Control Engineering，2009，(1)：1-6.(in Chinese))

[2] 邬 凯. 山区公路边坡地质灾害监测与预警系统研究[D].武汉：中国科学院武汉岩土力学研究所，2001.(WU Kai. Monitoring and Early Warning System for Geological Hazards of Mountainous Highway Slope[D]. Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences，2001.(in Chinese))

[3] 张桂荣，程 伟. 降雨及库水位联合作用下秭归八字门滑坡稳定性预测[J]. 岩土力学，2011，32(增刊1)：476-482.(ZHANG Gui-rong, CHENG Wei. Stability Prediction for Bazimen Landslide of Zigui County under the Associative Action of Reservoir Water Level Fluctuations and Rainfall Infiltration[J]. Rock and Soil Mechanics，2011，32(Sup.1)：476-482.(in Chinese))

[4] 唐满金. 降雨与库水位叠加作用下的库岸滑坡稳定性研究[J]. 中国水运，2007，5(10)：85-86.(TANG Man-jin. Stability of Reservoir Bank Slope under the Combined Action of Rainfall and Reservoir Water Level[J]. China Water Transport, 2007，5(10)：85-86.(in Chinese))

[5] 吴 琼，唐辉明，王亮清,等. 库水位升降联合作用下库岸边坡中的浸润线研究[J]. 岩土力学，2009，30(10)：3025-3031.(WU Qiong, TANG Hui-ming, WANG Liang-qing,etal. Analytic Solutions for Phreatic Line in Reservoir Slope with Inclined Impervious Bed under Rainfall and Reservoir Water Level Fluctuation[J]. Rock and Soil Mechanics，2009，30(10)：3025-3031.(in Chinese))

[6] 肖诗荣，刘德富，胡志宇. 三峡库区千将坪滑坡地质力学模型研究[J]. 岩土力学，2007，28(7)：1459-1464.(XIAO Shi-rong, LIU De-fu, HU Zhi-yu. Study on Geomechanical Model of Qianjiangping Landslide, Three Gorges Reservoir[J]. Rock and Soil Mechanics，2007，28(7)：1459-1464.(in Chinese))

[7] 孙冬梅，朱岳明，张明进. 库水位下降时的岸坡非稳定渗流问题研究[J]. 岩土力学，2008，29(7)：1807-1812.(SUN Dong-mei, ZHU Yue-ming, ZHANG Ming-jin. Research on Unsteady Seepage Problem of Bank Slope due to Drawdown of Reservoir Water Level[J]. Rock and Soil Mechanics，2008，29(7)：1807-1812.(in Chinese))

[8] FREDLUND D G，RAHARDJO H. 非饱和土土力学[M]. 陈仲颐，张在明，陈愈迥,等译，北京：中国建筑工业出版社，1997. (FREDLUND D G，RAHARDJO H. Unsaturated Soil Mechanics[M]. Translated by CHEN Zhong-yi, ZHANG Zai-ming, CHEN Yu-jiong,etal. Beijing: China Architecture & Building Press, 1997.(in Chinese))

[9] 张 华，陈善雄，陈守义. 非饱和土入渗的数值模拟[J]. 岩土力学，2003，24(5)：715-718.(ZHANG Hua, CHEN Shan-xiong, CHEN Shou-yi. Numerical Simulation of Infiltration in Unsaturated Soil[J]. Rock and Soil Mechanics，2003，24(5)：715-718.(in Chinese))

[10] 孟黔灵，姚海林，邱伦峰. 吸力对非饱和土抗剪强度的贡献[J]. 岩土力学，2001，22(4)：423-426.(MENG Qian-ling, YAO Hai-lin, QIU Lun-feng. The Contribution of Matric Suction to Shear Strength of Unsaturated Soils[J]. Rock and Soil Mechanics，2001，22(4)：423-426.(in Chinese))

[11] 吴俊杰，王成华，李广信. 非饱和土基质吸力对边坡稳定性的影响[J]. 岩土力学，2004，25(5)：732-737.(WU Jun-jie, WANG Cheng-hua, LI Guang-xin. Influence of Matric Suction in Unsaturated Soils on Slope Stability[J]. Rock and Soil Mechanics，2004，25(5)：732-737.(in Chinese))