HF-EMD频率选取原则及在暂态扰动检测中的应用

崔 艳，刘志刚，戴晨曦



HF-EMD频率选取原则及在暂态扰动检测中的应用

崔 艳，刘志刚，戴晨曦

(西南交通大学电气工程学院，四川成都 610031)

经验模态分解在处理电力系统暂态扰动信号时存在模态混叠的问题，基于高频谐波注入法的经验模态分解（简称HF-EMD）是一种简单高效的改进方法。该方法的有效性依赖于高频谐波频率的选取，而目前并没有有效的频率选取原则。着重对此问题进行了系统的研究，并通过理论分析和大量仿真试验得出了一个具体有效的选取原则: 当所注入的谐波频率在原信号高频成份的最小频率与该最小频率增加1/2倍基波频率的范围内时，HF-EMD普遍有效。对PSCAD模型仿真电能质量信号和变电站复杂实测扰动信号的分析表明，该原则具有高效性和普适性，能够有效提高暂态电能质量扰动信号的检测精度。

电能质量检测；经验模态分解；模态混叠；高频谐波注入法；频率选取原则

0 引言

电力系统中暂态电能质量问题，如脉冲暂态和振荡暂态等的发生，将造成某些电力设备绝缘破坏、电力电子设备损坏等不良后果，危害电网和电气设备安全、经济运行，影响居民正常生活。因此为保证电网的优质供电，有必要对其进行准确的检测，以实现监测和治理。对暂态电能质量的检测，目前应用最为广泛的是小波变换法及以此为基础的复合方法，该类方法分辨率高，理论成熟，但对小波基选取十分敏感，计算量较大且不具有自适应性。S变换具有比小波变换更细致的时频区分能力，但计算时间长、存储空间消耗大。

希尔伯特黄变换（Hilbert-Huang Transform, HHT）用于处理非线性非平稳信号，具有自适应性和精确识别能力，该方法首先通过经验模态分解(Empirical Mode Decomposition，EMD)将原信号分解为有限个固有模态函数（Intrinsic Mode Function， IMF），然后对每个IMF进行Hilbert变换，获取信号瞬时特征，具有较为明确的物理意义。文献[8-11]将HHT应用于各种电能质量检测中，效果显著。

大量研究表明EMD在处理电能质量信号时存在模态混叠的问题，使IMF不能真实地反映信号的物理意义。已有的改进方法大致可以分为三类：异常信号排除法处理实际信号有一定的效果，但会增加计算时间；信号滤波法处理过程复杂，不适合大量数据的分析处理；辅助信号注入法，文献[20]提出基于高频谐波注入法的EMD（HF-EMD），该方法过程简单，分解误差小，能够有效消除模态混叠，且运算速度快、不增加EMD复杂度，但其处理效果依赖高频谐波注入频率的选择，现有文献并没有给出具体的选取过程和方法，因而有必要对其进行系统而深入的研究，给出简单有效的频率选取原则以保证其应用的高效性和可靠性。

由于EMD所得IMF是由高频到低频排列，HF-EMD频率选取只需将注入高频谐波信号连同引起模态混叠的高频短时扰动作为第一个IMF分解出来，本文的频率选取过程为：首先对原信号进行小波滤波，其次对其高频成份求傅里叶频谱，此外选取不同的频率值分别进行HF-EMD，经大量仿真试验，得出有效的频率范围。最后，用基于该原则的HF-EMD分析PSCAD模型仿真电能质量信号和四川省某变电站实测复杂电能质量信号，验证了本文结果的实用性和有效性。

1 高频谐波注入法

1.1 EMD模态混叠问题

EMD本质上是一个自适应滤波过程，模态混叠的出现与其筛分过程有关，主要由某一或某几个时间尺度的本征模态函数不连续造成。电力系统暂态振荡、暂态脉冲等暂态扰动信号属于高频短时扰动，信号成份特征时间尺度相差极大，EMD在处理这类信号时，会出现同一个IMF中包含不同特征时间尺度的分量或者相近的特征时间尺度分布在不同的IMF中的现象，这种情况称为模态混叠。

对含脉冲、振荡的暂态扰动信号()、()分别进行EMD，其中基波频率50 Hz，原信号及所得前4个IMF如图1所示，从图中可以看出各IMF均出现了明显的模态混叠现象：IMF中分别包含了脉冲、振荡分量和部分本应出现在IMF的基波分量， IMF、IMF均包含两种或几种不同的特征时间尺度，相近的特征时间尺度在两个IMF中均有分布。模态混叠造成IMF的物理意义不明确。

1.2基于高频谐波注入法的改进EMD算法

由于EMD是一个从高频到低频的过程，高频信号总是出现在IMF中，且研究表明，IMF中往往包含了较宽的频率范围，而不是单一分量。若能将原信号中的高频扰动留在IMF中，后续分解将不再受其影响。

图1 含暂态扰动信号EMD结果图

HF-EMD方法就是通过在EMD之前向电力系统扰动原始信号注入适当的高频信号，改变原始信号的极值分布，削弱或“淹没”引起模态混叠的高频短时扰动成份，从而改善信号包络，提高EMD分解效果。该方法流程图如图2所示。

图2 HF-EMD流程图

HF-EMD所得第一个IMF为包含了所加高频谐波信号和原信号中高频短时扰动的分量，由于注入信号已知，需要时可以直接从第一个IMF减去，不影响对EMD结果的判断。该方法对信号中含特征时间尺度极大信号时，效果显著，但保证其有效性的关键是高频谐波信号的选取，而其频率（记为）的选取还没有统一的参考原则。

2 待注入高频谐波信号的选取

本文首先考虑各分量能量大小对EMD包络筛分的影响，得出大致有效的（记为）；然后考虑EMD不能分离频率较近的分量，得出有效选取范围。

2.1考虑高频能量的影响

由于EMD是求包络均值的筛分过程，获取信号包络取决于信号极值点的分布，而各分量能量大小影响信号极值点，因此高频成份各频率分量对应能量的不同对EMD过程有不同的影响。按能量变化随机选取不同的频率值，分别进行HF-EMD，对比分解效果，得出。

如图3所示为图1中信号()用本文所述方法求得高频成份频谱图，起始频率值为525 Hz，选取一系列不同幅值点对应频率值如表1所示，进行HF-EMD，结果如图4，=0 Hz对应不加高频谐波信号的EMD。从图中可以看出，当取高频起始频率点对应频率525 Hz时，振荡和基波成份分别被作为IMF和IMF正确分解，而取如=1 175、3 188 Hz等其他值时，振荡分量同时出现在IMF、IMF中，IMF频率成份混叠；=1 650、2 300、2 931 Hz、IMF总体上均体现信号中振荡成份特征，本应作为IMF分解出来的基波分量没有在前两阶中分离出来；=3 813、4 444、5 931 Hz时，IMF、IMF中高频成份甚至分布在整个采样时间段内，已无法辨时，IMF别各IMF特征。因此对()，有效频率值=525 Hz。

图3 x2(t)高频成份频谱图

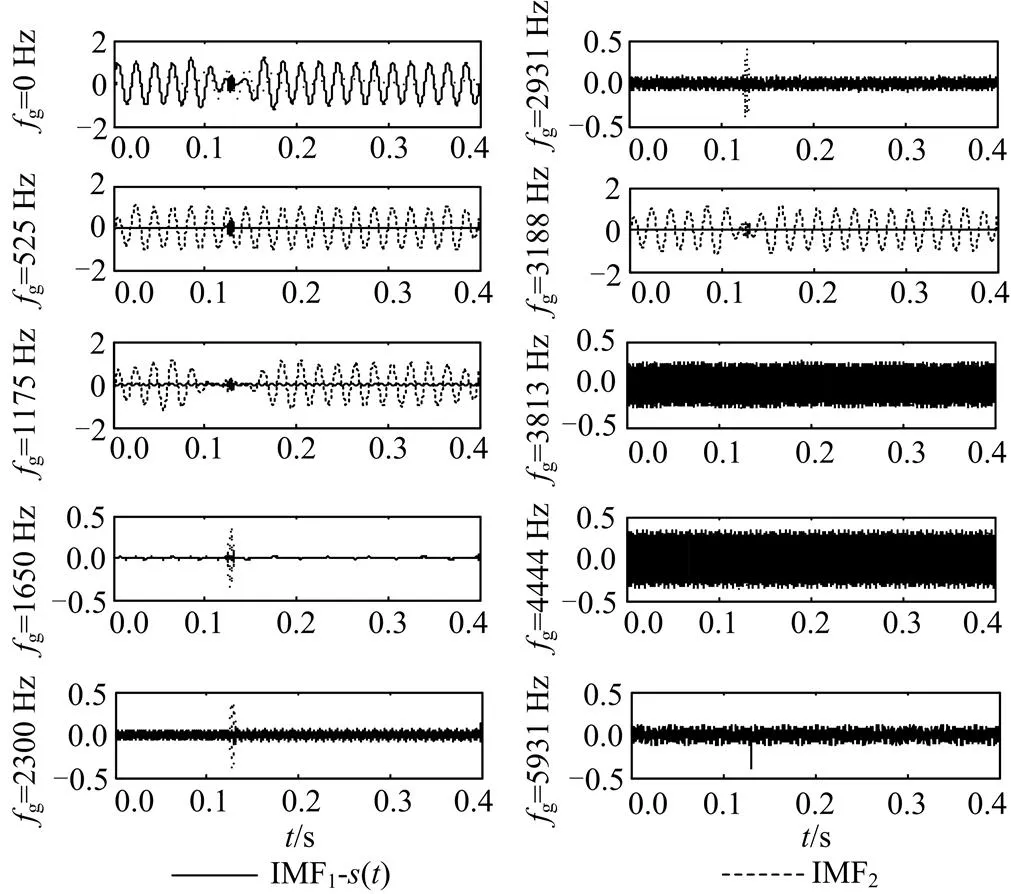
图4 HF-EMD结果图

表1 fg及对应能量取值表

由此，初步认为当扰动为特征时间尺度极大时，用HF-EMD方法消除模态混叠，有效应为高频成份最小频率值(记为)，对应频谱图中高频起始频率点（明显连续波动）。

2.2确定有效频率选取范围

由EMD是从高频到低频的分解过程，注入的高频谐波频率须高于信号中最小频率值，即应大于，以保证所加高频谐波在IMF中分解出来；同时有研究表明当信号中两分量频率0.5

对图1中信号()，在525~1 050 Hz范围内，随机选取了80个不同频率值进行HF-EMD，分析结果可知在该范围内取值并不都能消除模态混叠，依据模态混叠消除效果及其稳定性，可将该范围分为三个区间，对应处理效果见表2所示。图5为各区间部分分解效果。只有当取525至550 Hz时，信号中两种成份均被正确分解，HF-EMD方法稳定有效。

HF-EMD方法改善模态混叠有效频率值分布在以原信号中至2的范围内，且当频率值取至0.5范围内时，基本能全部起到改善效果。改变分析信号的暂态扰动类型、扰动频率、扰动幅值、扰动持续时间以及基波信号等，均得到与上述类似的结果，验证了本文方法的普遍适用性。由此可以认为高频注入频率有效的选取范围为：~0.5。

图5 确定有效频率范围HF-EMD结果图

表2 fg取值区间及HF-EMD效果

3 模型仿真验证

3.1电能质量扰动原始数据生成

在实际电网中，暂态脉冲主要由雷击、感性负荷投切等原因产生，暂态振荡主要由电容投切、电缆、架空线路投入等原因产生。本文基于PSCAD搭建220 kV输电线路简化模型，如图6所示，电源电压220 kV，工频50 Hz。为了满足分析要求采样频率设为6.4 kHz，采样时间0.3 s，采样第0.145 s在线路中投入10mF接地电容，获得含暂态振荡电流信号如图7所示，扰动在0.165 s结束，信号峰值为0.620 7 A，最大扰动幅值0.12 A。

图6 220 kV输电线路简化电路PSCAD模型

3.2 仿真分析

求取信号高频成份傅里叶频谱图如图7所示，高频起始频率值=700 Hz，构造高频谐波信号：()=0.6207sin(2π700) (A)。

分别用传统EMD和HF-EMD对仿真信号进行分解，均得到6个IMF分量，结果如图8所示。图中列出前4个IMF。比较分解结果，图8(a)所示传统的EMD不能将仿真信号各成份有效分离，模态混叠使IMF无法表示真实的物理过程： IMF、IMF均包含不同特征时间尺度的分量；IMF与IMF中分布有相近特征时间尺度的分量，使得IMF物理意义无法明确判断。图8(b)所示HF-EMD较之有非常明显的改进效果：IMF对应信号中暂态振荡成份，IMF对应信号中低频正弦成份，IMF值很小视为残差，模态混叠得到有效消除。

图7 仿真信号及其高频成份频谱图

图8 仿真信号EMD和HF-EMD结果图

已知该仿真信号基波频率为50 Hz，则基于本文研究结果的有效频率选取范围为700~725 Hz，随机选取该范围内一组频率值作为，分别进行HF-EMD，结果如图9。可以看出信号中振荡、基波成份分别作为IMF、IMF得到有效分离，HF-EMD均能有效消除模态混叠现象，验证了本文经验选取原则的可行性。

在有效范围外随机选取一组数据进行HF-EMD，对比各方法结果如表3所示，可知在有效频率范围内的HF-EMD不仅能改善模态混叠，且分解所得IMF个数与EMD方法基本一致，没有增加原方法的复杂度，运算时间相比缩短，提高了算法效率，而在有效范围外的HF-EMD不能起到明显的改善效果。

图9 仿真信号HF-EMD结果图

表3 各方法结果对比

3.3扰动检测

分别对图8中EMD与HF-EMD所得IMF进行Hilbert变换，检测扰动信息，并与小波法检测结果进行对比，结果如图10和表4所示。图10中()、()依次为EMD、HF-EMD方法下所得瞬时频率，()、()为瞬时幅值，图10(e)为小波法检测结果。

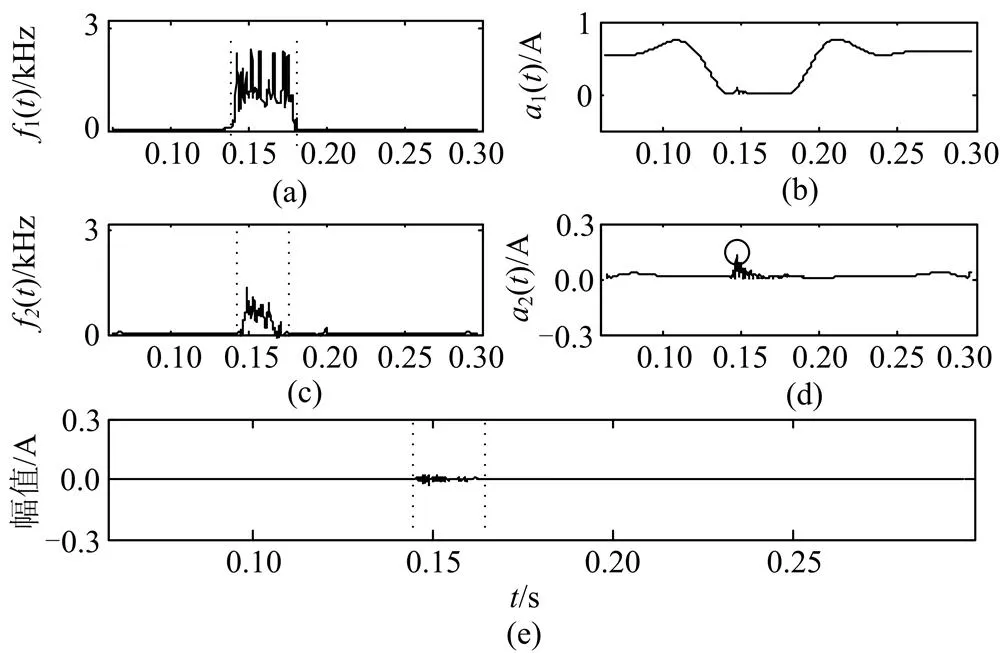
图10 仿真信号扰动检测图

表4 仿真信号扰动检测结果表

由表4可以看出采用HF-EMD的HHT方法定位扰动起止时刻更准确，检测精度高于小波分析法。由于EMD的模态混叠现象，传统方法不能得到有效的扰动幅值信息，采用HF-EMD和小波能检测到最大扰动幅值，但前者检测结果误差更小。因此经HF-EMD之后再Hilbert变换的HHT方法检测电能质量扰动的精度更高。

4 实测数据验证

为进一步验证本文选取原则的实际可行性，对四川省某110 kV变电站某日下午17：16现场实测电能质量信号进行分析，采样频率25.6 kHz，采样时间0.6 s，如图11中()所示。考虑实际信号的复杂性，先对原信号进行消噪处理，然后分别用EMD、有效频率范围内HF-EMD对其进行分解，其中注入高频谐波()=91.861sin(2π2246) (kV)，分解结果如图11所示，HHT扰动检测结果如图12和表5所示。可以看出基于本文频率选取原则的HF-EMD对实测信号处理效果良好，基于此的HHT检测实际扰动信号的方法可行。

图11 实测信号EMD和HF-EMD结果图

图12 实测信号扰动检测图

表5 实测信号扰动检测结果表

5 结论

本文采用高频谐波注入法对EMD方法分解暂态振荡、暂态脉冲等含特征时间尺度极大的电能质量信号时产生的模态混叠问题进行改进，着重讨论了待注入高频谐波信号频率的选取方法。大量的仿真试验表明，有效频率值分布在以原信号中高频部分最小频率值为起点，两倍基波频率大小的范围内，且当频率值取高频成份最小频率至1/2倍基波频率范围内时，得到较好的改善效果。运用基于本文提出选取原则的HHT方法对含暂态振荡信号进行分析和检测，HF-EMD能高效消除EMD方法分解时存在的模态混叠问题，扰动起止时间和幅值信息得到较准确的检测。

[1] 胡铭, 陈珩. 电能质量及其分析方法综述[J]. 电网技术, 2000, 24(2): 36-38.

HU Ming, CHEN Heng. Survey of power quality and its analysis methods[J]. Power System Technology, 2000, 24(2): 36-38.

[2] 曾德良, 刘继伟, 柳玉, 等. 小波多尺度分析方法在磨辊磨损检测中的应用[J]. 中国电机工程学报, 2012, 32(23): 126-131, 160.

ZENG De-liang, LIU Ji-wei, LIU Yu, et al. The application of wavelet multi-scale analysis for wear characteristics[J]. Proceedings of the CSEE, 2012, 32(23): 126-131, 160.

[3] 易建波, 黄琦, 丁理杰, 等. 提升经验模态分解检测低频振荡模式精度的改进算法研究[J]. 电力系统保护与控制, 2013, 41(22): 71-78.

YI Jian-bo, HUANG Qi, DING Li-jie, et al. Research on an improved algorithm to enhance the detection accuracy of low-frequency oscillation modes by empirical mode decomposition[J]. Power System Protection and Control, 2013, 41(22): 71-78.

[4] WANG D, MIAO Q, FAN X F, et al. Rolling element bearing fault detection using an improved combination of Hilbert and wavelet transforms[J]. Journal of Mechanical Science and Technology, 2009, 23(12): 3292-3301.

[5] 张扬, 刘志刚. 一种基于时频域多特征量的电能质量混合扰动分类新方法[J]. 中国电机工程学报, 2012, 32(34): 83-90.

ZHANG Yang, LIU Zhi-gang. A new method for power quality mixed disturbance classification based on time-frequency domain multiple features[J]. Proceedings of the CSEE, 2012, 32(34): 83-90.

[6] 刘毅力, 陶学军, 李佳, 等. 基于HHT的风力发电机组滚动轴承故障特征提取[J]. 电力系统保护与控制, 2012, 40(20): 79-82, 88.

LIU Yi-li, TAO Xue-jun, LI Jia, et al. Feature extraction of rolling bearing for wind generator based on HHT[J]. Power System Protection and Control, 2012, 40(20): 79-82, 88.

[7] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 45(4): 903-995.

[8] 苏玉香, 刘志刚, 李科亮, 等. Hilbert-Huang变换在电气化铁路谐波检测中的应用[J]. 电网技术, 2008, 32(18): 30-35.

SU Yu-xiang, LIU Zhi-gang, LI Ke-liang, et al. Application of Hilbert-Huang Transform in harmonic detection of electrified railway[J]. Power System Technology, 2008, 32(18): 30-35.

[9] 刘兴茂, 何正友. 基于希尔伯特-黄变换的输电线路距离保护方案[J]. 电力系统自动化, 2013, 37(2): 108-112.

LIU Xing-mao, HE Zheng-you. Distance protection scheme for transmission lines based on Hilbert-Huang Transform[J]. Automation of Electric Power Systems, 2013, 37(2): 108-112.

[10] BROWNE T J, VITTAL V, HEYDT G T, et al. A comparative assessment of two techniques for modal identification from power system measurements[J]. IEEE Trans on Power Systems, 2008, 23(3): 1408-1415.

[11] SENROY N, SURYANARAYANAN S, RIBEIRO P F. An improved Hilbert-Huang method for analysis of time-varying waveforms in power quality[J]. IEEE Trans on Power Systems, 2007, 22(4): 1843-1850.

[12] 李成鑫, 刘俊勇, 姚良忠, 等. 基于改进频移经验模态分解的低频振荡参数提取[J]. 电力系统自动化, 2012, 36(15): 8-13.

LI Cheng-xin, LIU Jun-yong, YAO Liang-zhong, et al. Extraction of low frequency oscillation parameters based on refined frequency shift empirical mode decomposition[J]. Automation of Electric Power Systems, 2012, 36(15): 8-13.

[13] 张宇辉, 贺健伟, 李天云, 等. 基于数学形态学和HHT的谐波和间谐波检测方法[J]. 电网技术, 2008, 32(17): 46-51.

ZHANG Yu-hui, HE Jian-wei, LI Tian-yun, et al. A new method to detect harmonics and inter-harmonics based on mathematical morphology and Hilbert-Huang Transform [J]. Power System Technology, 2008, 32(17): 46-51.

[14] MESSINA A R, VITTAL V, HEYDT G T, et al. Nonstationary approaches to trend identification and denoising of measured power system oscillations[J]. IEEE Trans on Power Systems, 2009, 24(4): 1798-1807.

[15] SAWALHI N, RANDALL R B. Spectral Kurtosis optimization for rolling element bearings[C] // Signal Processing and Its Applications. Sydney: Proceedings of the Eighth International Symposium on, 2005: 839-842.

[16] 黄迪山. 经验模态分解中虚假模态分量消除法[J].振动、测试与诊断, 2011, 31(3): 381-384.

HUANG Di-shan. Effect of sampling on empirical mode decomposition and correction[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3): 381-384.

[17] 姚林朋, 郑文栋, 钱勇, 等. 基于集合经验模态分解的局部放电信号的窄带干扰抑制[J]. 电力系统保护与控制, 2011, 39(22): 133-139.

YAO Lin-peng, ZHENG Wen-dong, QIAN Yong, et al. A narrow-band interference suppression method based on EEMD for partial discharge[J]. Power System Protection and Control, 2011, 39(22): 133-139.

[18] 刘志刚, 李文帆, 孙婉璐. Hilbert-Huang 变换及其在电力系统中的应用[J]. 电力自动化设备, 2012, 32(4): 109-116.

LIU Zhi-gang, LI Wen-fan, SUN Wan-lu. Hilbert-Huang Transform and its applications in power system[J]. Electric Power Automation Equipment, 2012, 32(4): 109-116.

[19] WU Zhao-hua, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[20] 李天云, 赵妍, 李楠, 等. 基于HHT的电能质量检测新方法[J]. 中国电机工程学报, 2005, 25(17): 52-56.

LI Tian-yun, ZHAO Yan, LI Nan, et al. A new method for power quality detection based on HHT[J]. Proceedings of the CSEE, 2005, 25(17): 52-56.

[21] HUANG N E. Introduction to the Hilbert-Huang transform and its related mathematical problems[J]. Hilbert-Huang Transform and Its Applications, 2005: 1-26.

[22] ABDEL-GALIL T K, KAMEL M, YOUSSEF A M, et al. Power quality disturbance classification using the inductive inference approach[J]. IEEE Trans on Power Delivery, 2004, 19(4): 1812-1818.

Frequency selection principle of HF-EMD and its application in transient disturbance detection

CUI Yan, LIU Zhi-gang, DAI Chen-xi

(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Modal aliasing problem exists in empirical mode decomposition for the decomposition of transient power quality disturbances, and high-frequency harmonic injection based EMD (HF-EMD) is a simple and efficient method to improve it. The effectiveness of this method depends on the selection of the frequency of the high-frequency harmonic, and there is no effective frequency selection principle. Focusing on this problem, this paper conducts a systematic study, and through theoretical analysis and simulation test, a concrete and effective selection principle is presented. That is to say, when the injected frequencies are in the range from the smallest frequency of the original signal’s high-frequency components to adding a 1/2 times fundamental frequency of the smallest frequency, HF-EMD shows general validity. The analysis of power quality signals simulated by PSCAD and the actual complex disturbance signals of substation shows that this principle is efficient and universal. The detection accuracy of transient power quality disturbances can be effectively improved.

This work is supported by National Natural Science Foundation of China (No. U1134205 and No. 51377136).

power quality detection; EMD; modal aliasing; high-frequency harmonic injection; frequency selection principle

TM76

A

1674-3415(2014)21-0047-07

2014-01-24

崔 艳（1991-），女，硕士研究生，主要研究方向为现代信号处理理论及其在电力系统中的应用；E-mail: cy_kuaile123@126.com

刘志刚（1975-），男，教授，博士生导师，主要研究方向为现代信号处理与智能计算及其在电力系统中的应用；

戴晨曦（1991-），女，硕士研究生，主要研究方向为基于MBD的牵引供电系统故障诊断。

国家自然科学基金(U1134205,51377136)