基于内点法的交直流混联系统抗差状态估计
2014-08-16郑伟业吴文传张伯明孙宏斌
郑伟业,吴文传,张伯明,孙宏斌
基于内点法的交直流混联系统抗差状态估计
郑伟业,吴文传,张伯明,孙宏斌
(电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京 100084)
针对交直流混联系统的状态估计问题,分析了其数学模型,对其求解方法进行了研究,并开发了软件。介绍了交直流混联系统的抗差状态估计模型,根据该模型的特点进行变量等价转换,以降低其复杂度。在利用内点法进行求解时,通过对原问题的海森矩阵进行近似,确保其正定且提升了算法的效率。通过IEEE 9节点、14节点、30节点、118节点、145节点系统这5个算例,分析了算法效率以及收敛域。结果表明,与牛顿法相比,基于内点法的状态估计的收敛域更宽广,可以应对更恶劣的现场状况,具备现场应用潜力。
电力系统;交直流混联系统;内点法;抗差状态估计
0 引言
高压直流输电在我国发展迅速,例如南方电网已建设成世界上最复杂的交直流混联电网。交直流的状态估计比纯交流的问题,要更为复杂,更难求解。从1980年开始,出现了有关交直流互联电网状态估计的研究。文献[1]对于20世纪状态估计问题的研究状况作出了系统性的总结。按照求解思路可分为整体求解法和解耦求解法这两类。
(1)整体求解法
整体求解法把交直流部分统一纳入状态估计的数学模型中,并且不考虑他们之间的解耦。文献[2]提出交直流互联系统状态估计的概念并给出了实际算例,但是,该文并没有为换流器建模。文献[3]对量测方程进行泰勒展开,并且只保留至二阶,使状态估计在迭代过程中的信息矩阵变为定常阵,对交直流系统进行整体建模,然后一起进行状态估计。
总体来说,整体求解法收敛性好,而且建模简单,缺点是求解起来难度较大,计算量大。
(2)解耦求解法
解耦求解法则在数学建模的时候,把原系统分成相互独立的部分,以减小问题的求解规模和复杂度,同时又可以沿用原有交流系统的状态估计程序。文献[4]首先提出基于双端直流系统的有功-无功-直流顺序迭代的交直流估计算法。文献[5]把交直流混联系统解耦为直流网络、交流网络以及交直流网络互联部分,并对这三部分分别进行计算,求出状态估计的次优解。文献[6]采用了主从分裂的算法,考虑了交直流之间的耦合关系,但是,并没有提供理论上的收敛性证明。文献[7]利用高斯消去法,把直流部分对交流部分的影响在信息矩阵中消去,而对于直流部分,则把交流的耦合放到量测方程右侧,从而实现交直流的解耦。
简而言之,解耦求解法求解方法简单,可以部分沿用先前的程序,但是建模技巧性要求高,不恰当的简化与假设会给结果带来误差,并且,在交替迭代的过程中经常会遇到不收敛的问题。
传统状态估计一般采用牛顿法,但是,在现场应用中发现,在重载等等恶劣情况下,牛顿法存在收敛性问题。牛顿法存在对初值敏感、收敛域窄的不足,以及无法考虑多种复杂不等式约束和等式约束的缺点,内点法以及其变种算法在电力系统中得到了日益广泛的应用。其中,文献[14-17]是内点法在电力系统状态估计中的应用。
本文把文献[18]提出的抗差状态估计模型推广到交直流混联系统中,并采用内点法对交直流混联系统进行整体求解。本文主要工作有以下三点:
(1)提出了变量等价转换的方法,对原抗差状态估计模型进行转换,降低其复杂度;
(2)开发了基于内点法的交直流混联系统抗差状态估计的程序,用算例验证了其宽广的收敛域;
(3)提出了近似海森矩阵的方法,算例结果表明,这可以有效提升算法效率。
1 抗差状态估计模型及其等价变量转换
在文献[18]中提出的抗差状态估计模型,可描述成以下形式。
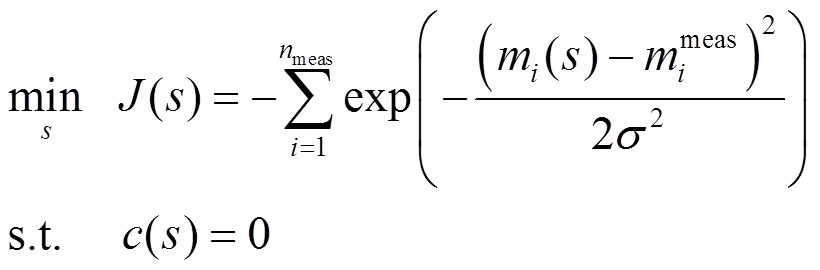

因此需要对原抗差状态估计模型进行等价转换,引入残差变量
(3)
则式(1)所描述的模型可以转换为以下模型。

其中:的状态量;的定义如式(3)所示。
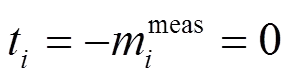
即可满足零注入约束。
做了这样的变换之后,把量测方程放在等式约束中,而在目标函数中只保留残差变量,那样雅可比矩阵各元素的表达式被极大地简化了。

(7)
(8)
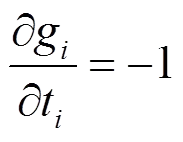
海森矩阵各元素的表达式也变得简洁不少,且大量元素变为0。
(10)

(12)
(13)

(15)
这样变换可以大大降低程序编写难度。
此外,只需要少量的代码改动,即可实现状态估计模型的转换。因为在式(4)的模型下,不同状态估计器之间的区别只在于目标函数,量测方程的等式约束都是一样的。例如,实现最常见的加权最小二乘,只需把式(4)的目标函数改为
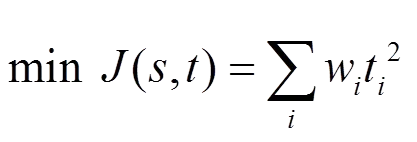
等式约束部分无需改动。
这时雅可比矩阵的元素只修改式(7)。

海森矩阵的元素也只需要修改式(12)。
(18)
而雅可比矩阵以及海森矩阵其余元素均无需改动。
2 交直流混联电网的整体建模
双端直流输电系统如图1所示。
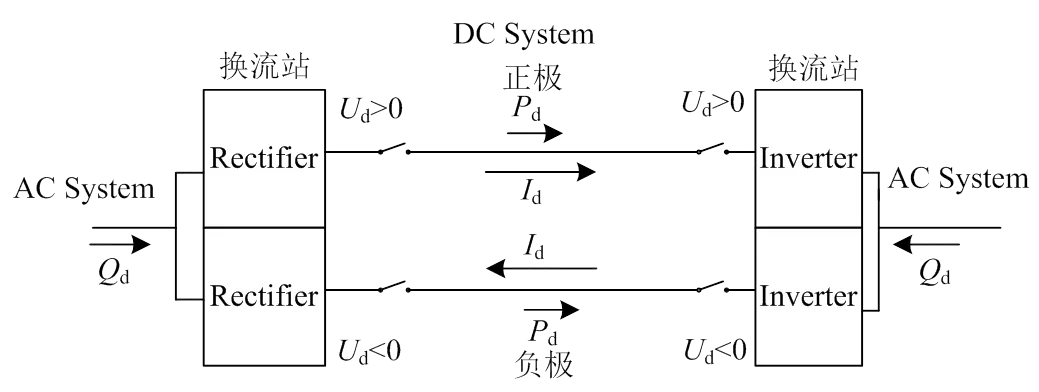
图1 双端直流输电系统
双端高压直流输电系统本质上可以看成是双端口元件,潮流的参考方向和电流的参考方向均取流入高压直流系统为正方向。
在此列出直流内部的量测方程(上标m表示量测)为

(20)
(21)

(23)
(24)
交直流边界处的量测方程为

(26)
式(20)和式(26)所示的无功功率量测方程中含有根号项,在内点法在迭代的过程其并不总在该函数的定义域内,因此会造成程序错误。
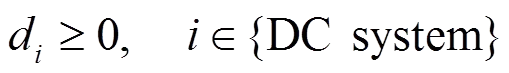
(28)
这样,可以避免在迭代过程中引起计算错误。与此同时,原来的直流支路无功功率方程则变为

3 内点法求解过程以及海森矩阵的近似
采用原始-对偶内点法来对式(4)的模型进行求解,算法流程如下。
(1)为了简明起见,把式(4)的模型改写成标准型为
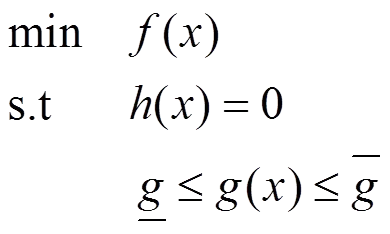
其中:是状态量和残差变量合并后的复合向量,;函数()包含所有等式约束;()包含所有不等式约束。
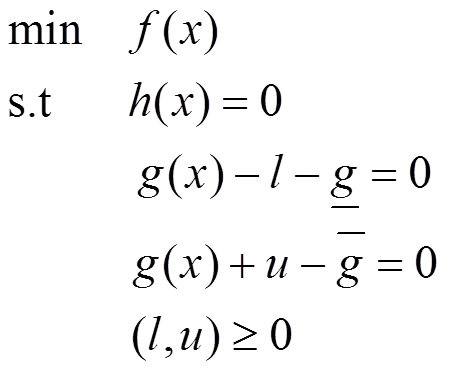
其中,为函数()的维数。
(3)构建增广拉格朗日函数为

(4)设置迭代初始值,将原始变量中,状态量中的电压幅值初值设为1,电压相角初值设为0,将残差变量的初始值设为0,将对偶变量的初始值设为0,设置迭代次数,设置最大迭代次数,的取值范围为:10~100,对于零注入母线,设定残差变量的第个分量。
(6)如果=1,则直接进行步骤(7)。

其中:和为松弛变量;和为对偶变量;为函数()的维数。

(8)按照以下KKT方程组,计算上述增广拉格朗日函数对原-对偶内点法中各原始变量和对偶变量的一阶偏导数为
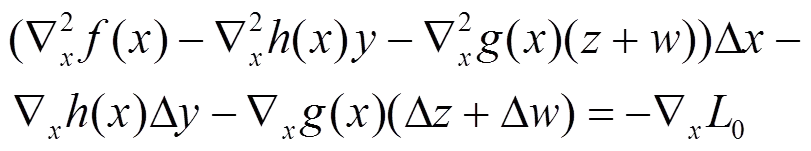
(35)

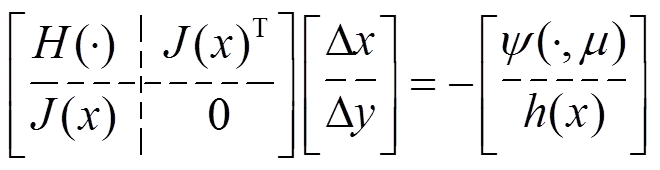
(36)
其中:

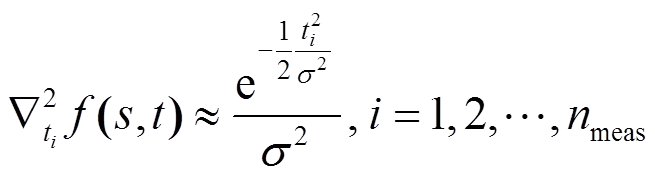
以保持海森矩阵正定进行迭代。
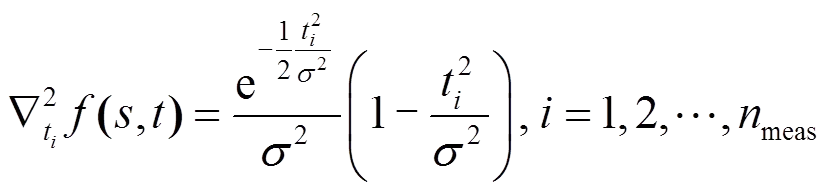
此时一般t较小,海森矩阵正定性可以得到满足,沿下降方向寻找最优解。
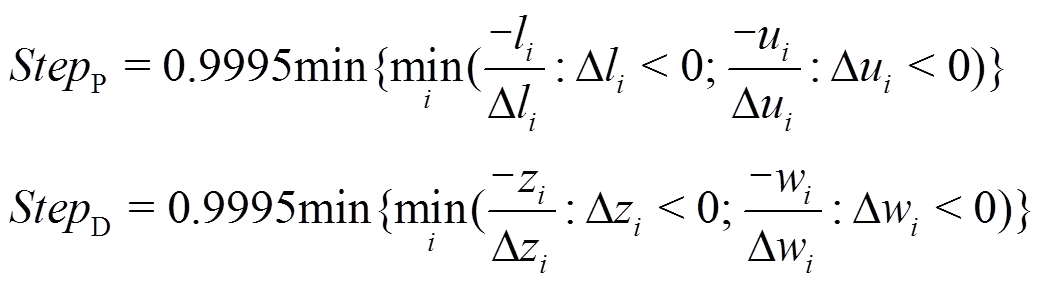
(11)根据步骤(10)的修正步长,更新上述原始变量和对偶变量, 使
(40)
(12)重复步骤(5)。
4 算例分析
(1)内点法和牛顿法收敛域的对比
为了验证性能,开发了基于上述方法的程序,程序中调用了基于原始-对偶内点法的开源包IPOPT(内点法优化包)来求解交直流混联抗差状态估计模型。测试系统的硬件环境为英特尔双核i5-3210 M CPU 2.50 GHz,8 GB内存,操作系统为Win7 64 bit,开发环境为Visual Studio 2008,IPOPT版本为3.5.5。
以IEEE 30节点标准测试系统为算例,核估计法的窗宽按经验设为(也可设为别的值),电压相角初值均选为0,基于同样的抗差状态估计模型,分别对内点法和牛顿法的收敛域作对比。针对相同数学模型,这两种求解算法,在收敛的情况下可以得到相同的结果。在此处关心的是两种算法的收敛域的区别。
从表1可见内点法的收敛域比牛顿法更宽广,也就意味着内点法更为鲁棒,能在质量恶劣的初值下迅速收敛。这是因为内点法引入了罚函数,当状态量在可行域之外时,罚函数能把状态量压回可行域内。而牛顿法遇到这种情况,可能就会发散。

表1 内点法和牛顿法收敛域对比
内点法优良的收敛性能是具有现实意义的。在极端的现场情况下,牛顿法的程序有时会不收敛。例如,负荷水平过高或过低时,节点电压幅值会偏离标准电压较远,但状态估计设初值一般采用平启动,由于牛顿法收敛域较窄,这时可能就不收敛了。而如果采用内点法来计算,就有可能应对这些极端情况。
依然以IEEE 30节点标准测试系统为算例,核估计法的窗宽不变,调节负荷水平,采用平启动,对内点法和牛顿法两种算法的收敛域做对比,结果如表2所示。

表2 不同负荷水平下内点法和牛顿法收敛域对比
(2)近似海森矩阵的效果
虽然基于内点法的抗差状态估计程序具有更宽广的收敛域,但是在程序调试时发现,如果一直采用精确的海森矩阵,当系统规模较大时(例如对于IEEE 145节点系统),程序的迭代次数过多,以至于计算的效率较低。为了提高效率,使得内点法更加可能满足现场对状态估计的实时性的需求,本文提出了加速算法的一种方法——在迭代前期对海森矩阵采用式(38)的近似。
为了验证这种方法的效果,以145节点标准测试系统为算例,对两种情况作对比:
1)不近似:一直采用精确的海森矩阵进行计算;
2)近似:在迭代前期对海森矩阵作式(38)的近似处理,转换阈值设为计算精度的2倍。当互补间隙时,就采用精确的海森矩阵。
得到结果如表3和图2所示。

表3 迭代次数对比
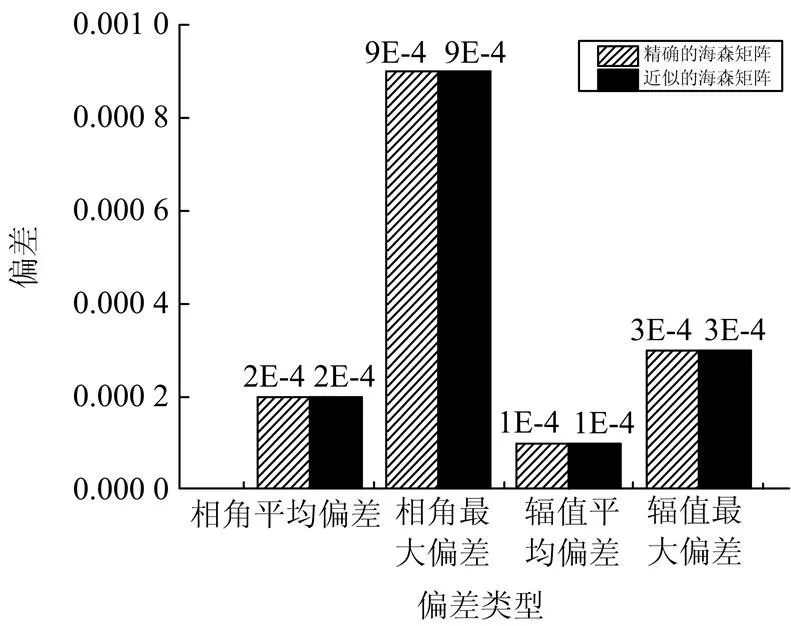
图2 估计精度对比
可见,在迭代初期对海森矩阵作数值近似,能有效地减少迭代次数,提高了求解效率,同时不影响状态估计的求解精度。
下面对IEEE 9节点系统、14节点系统、30节点系统、118节点系统、145节点系统共5个标准系统进行测试,窗宽按经验取,采用平启动方式,再对近似和不近似的两种情况进行测试。计算时间如图3所示。

图3 不同规模系统下的计算时间
5个系统的结果均表明,近似海森矩阵是一种加速算法的有效方法。
(3)抗差性能
在此处验证一下该程序在交直流混联系统中的抗差性能。请注意,抗差性能只与数学模型有关,而与算法的实现无关。如果计算精度设定一致,而且结果收敛的话,牛顿法和内点法的计算结果是一样的。跟牛顿法相比,内点法的优点是收敛域更宽,如前文所述。
把IEEE 30节点标准测试系统的其中一条线路换成直流线路,得到交直流混联系统,其结构图如图4所示。其中,节点10、20之间的直流线路参数如表4~表6。

图4 30节点交直流混联系统结构图
为了测试,在量测值加上一个服从(0,0.01)正态分布的随机误差,核估计法的窗宽也取为0.01,则当坏数据比例从0逐渐增至10%时,可得估计结果如表7。

表4 30节点交直流混联系统的直流线路参数(A)

表5 30节点交直流混联系统的直流线路参数(B)

表6 30节点交直流混联系统的直流线路参数(C)

表7 30节点算例计算结果
可见式(4)的模型应用到交直流混联系统中,依然有较强的抗差性。
5 结论
传统的牛顿法存在收敛域窄的问题,为了克服这个缺点,本文从研究对象、状态估计模型、求解算法三方面着手,以指数型目标函数为抗差估计模型,对交直流混联电网进行整体建模,并基于内点法开发了一套抗差状态估计程序。
本文提出的等价转换的技巧,简化了程序编写的难度。此外,算例表明,采用内点法来做抗差状态估计,具有比牛顿法更为宽广的收敛域,在质量极为恶劣的初值下也能迅速收敛,能应对现场出现的极端情况。
内点法的抗差状态估计程序目前存在效率较低的问题,为此,本文提出一种加速算法的方法——近似海森矩阵,并从理论和仿真实验两方面说明其有效性。
本文工作还需要从理论上对算法效率进行研究,对Parzen窗宽进行自适应调整,进一步加速算法,以供现场大规模互联电网使用。
[1] 李碧君, 薛禹胜, 顾锦汶, 等. 电力系统状态估计问题的研究现状和展望[J]. 电力系统自动化, 1998, 22(11): 53-60.
LI Bi-jun, XUE Yu-sheng, GU Jin-wen, et al. Status quo and prospect of power system state estimation[J]. Automation of Electric Power Systems, 1998, 22(11): 53-60.
[2] GLOVER J D, SHEIKOLESLAMI M. State estimation of interconnected HVDC/AC systems[J]. IEEE Power Engineering Review, 1983, 3(6): 55-56.
[3] HAQUE M Z, KALAM A. Second-order AC-DC power system state estimator[J]. International Journal of Power & Energy Systems, 1997, 17(2): 138-144.
[4] SIRISENA H R, BROWN E P M. Inclusion of HVDC links in AC power-system state estimation[J]. IEE Proceedings on Generation, Transmission and Distribution, 1981, 128(3): 147-154.
[5] LEITE DA SILVA A M, PERROTTA G, PRADA R B, et al. State estimation for integrated multi-terminal DC/AC systems[J]. IEEE Trans on Power Apparatus and Systems, 1985, 104(9): 2349-2355.
[6] 李大志. 南方电网交直流混合状态估计的研究[D]. 北京: 清华大学, 2008.
LI Da-zhi. Study on state estimation of the AC/DC hybrid power system in China Southern Power Grid[D]. Beijing: Tsinghua University, 2008.
[7] DING Qi-feng, CHUNG T S, ZHANG Bo-ming. An improved sequential method for AC/MTDC power system state estimation[J]. IEEE Trans on Power Systems, 2001, 16(3): 506-512.
[8] KARMARKAR N. A new polynomial-time algorithm for linear programming[C] // Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing, 1984: 302-311.
[9] MONTEIRO R D C, ADLER I, RESENDE M G C. A polynomial-time primal-dual affine scaling algorithm for linear and convex quadratic programming and its power series extension[J]. Mathematics of Operations Research, 1990, 15(2): 191-214.
[10]钟世霞, 袁荣湘. 内点法在电力系统中的应用述评[J]. 高电压技术, 2005, 31(12): 76-79.
ZHONG Shi-xia, YUAN Rong-xiang. An application of interior point method in optimization of power systems [J]. High Voltage Engineering, 2005, 31(12): 76-79.
[11] 王剑, 刘天琪, 刘学平. 基于优先级排序和内点法的机组优化组合[J]. 电力系统保护与控制, 2010, 38(13): 55-60.
WANG Jian, LIU Tian-qi, LIU Xue-ping. Unit commitment optimization based on priority list and interior point methods[J]. Power System Protection and Control, 2010, 38(13): 55-60.
[12] 姚煜, 蔡燕春. 离散粒子群与内点法结合的电力系统无功优化[J]. 电力系统保护与控制, 2010, 38(3): 48-52.
YAO Yu, CAI Yan-chun. A hybrid strategy based on DPSO and IPM for optimal reactive power flow[J]. Power System Protection and Control, 2010, 38(3): 48-52.
[13] 张锋, 段余平, 邱军, 等. 基于粒子群算法与内点算法的无功优化研究[J]. 电力系统保护与控制, 2010, 38(13): 11-16.
ZHANG Feng, DUAN Yu-ping, QIU Jun, et al. Research on reactive power flow based on particle swarm optimization and interior point method[J]. Power System Protection and Control, 2010, 38(13): 11-16.
[14] SINGH H, ALVARADO F L. Weighted least absolute value state estimation using interior point methods[J]. IEEE Trans on Power Systems, 1994, 9(3): 1478-1484.
[15] JABR R A. Primal-dual interior-point approach to compute the solution of the state estimation problem[J]. IEE Proceedings on Generation, Transmission and Distribution, 2005, 152(3): 313-320.
[16] 王雅婷, 何光宇, 刘铠诚, 等. 求解状态估计问题的内点半定规划法[J]. 电网技术, 2012, 36(10): 209-215.
WANG Ya-ting, HE Guang-yu, LIU Kai-cheng, et al. An semi-definite programming method for state estimation problem[J]. Power System Technology, 2012, 36(10): 209-215.
[17] RAMIREZ-ARREDONDO J M, BAROCIO E E, CHACON O L. The affine-scaling dual algorithm as an alternative to solve the power system state estimation problem[J]. IEEE Power Engineering Review, 1999, 19(6): 50-52.
[18] WU Wen-chuan, GUO Ye, ZHANG Bo-ming, et al. A robust state estimation method based on maximum exponential square (MES)[J]. IET Generation, Transmission & Distribution, 2011, 5(11): 1165-1172.
Robust state estimator for AC/DC hybrid power system based on an interior point method
ZHENG Wei-ye, WU Wen-chuan, ZHANG Bo-ming, SUN Hong-bin
(State Key Lab of Power Systems, Dept of Electrical Engineering, Tsinghua University, Beijing 100084, China)
A robust SE model is introduced for AC/DC hybrid system. First, to simplify its formulation, the SE model is transformed into an equivalent form by introducing equality constraints and new variables. In this model, the hybrid system is formulated as a whole. Then, an interior point method is used to solve this problem. And an approximating technique is proposed to guarantee the Hessian matrix positive definite, which can significantly improve the efficiency of the solution. Five numerical tests with IEEE 9 node system, IEEE 14 node system, IEEE 30 node system, IEEE 118 node system, and IEEE 145 node system show that the proposed algorithm is efficient, robust and reliable. It has the potential to be applied in real application.
This work is supported by National Key Basic Research Program of China (973 Program) (No. 2013CB228203).
power system; AC/DC hybrid system; interior point method; robust state estimation
TM71
A
1674-3415(2014)21-0001-08
2014-02-19;
2014-03-12
郑伟业(1990-),男,博士生,研究方向为电力系统状态估计、分布式自律优化与控制;E-mail: neo_adonis@139.com
吴文传(1973-),男,博士,教授,博士生导师,主要从事控制中心自动化系统的研究和教学工作;
张伯明(1948-),男,博士,教授,博士生导师,IEEE Fellow,主要从事电力系统运行、分析和控制的研究工作。
国家重点基础研究发展计划(973 计划)(2013CB228203)
