基于AHP-DEA模型的电网规划方案综合评判决策

陈 奎，韦晓广，牛俊萍，陈景波



基于AHP-DEA模型的电网规划方案综合评判决策

陈 奎，韦晓广，牛俊萍，陈景波

(中国矿业大学信息与电气工程学院，江苏 徐州 221008)

针对电网规划方案综合评判决策的复杂性以及层次分析法（AHP）的主观性过强和数据包络法（DEA）无法体现决策者偏好的缺陷，提出了一种AHP和DEA相融合的方法。将该方法依据是否融合灰色关联度又分别建立两种模型。通过建立电网规划综合评判体系，运用两种模型对一个实际电网规划问题进行求解分析，计算结果与实际期望方案一致。在此基础上对模型进行容错性分析，分析表明融合灰色关联度的AHP-DEA模型相比其他模型具有较强的容错性能，在遭到非正常因素的干扰下仍能选出最优方案。

电网规划；层次分析法（AHP）；数据包络法（DEA）；灰色关联；超效率；容错性能

0 引言

电网规划是电力行业正常运行的重要保证。一个地区的电网运作是否良好直接取决于电网规划是否科学和合理。随着电力市场的逐步形成，电网规划不再是单一性目标，而是一个多目标的复杂性的非线性决策过程。另外，它受到多方面因素的制约，例如经济性、技术性、环境性等因素直接决定电网的实际规划。

现今，解决电网规划的难题主要有：1）电网规划的指标众多，这些指标中有些是定量指标，有些是定性指标，准确量化各指标是科学合理规划电网的重要保证；2）电网规划受到多指标的制约，不仅仅取决于技术性、同时要综合考虑投资者的经济性以及地区环境因素的影响，因此，如何平衡各指标是电网规划的前提。

目前，电网规划评估方法众多，但概括起来主要有两大类。1）以决策者主观判断为主的评估方法（下文简称主观评价法），主要代表为层次分析法（AHP）。2003年，陈大宇等人提出了模糊AHP，通过将AHP中的专家评分用模糊数替代，减少主观判断的不确定性；2004年，肖峻等人把区间AHP应用于电网规划，该方法改进了层次分析法中的区间判断矩阵一致性的校验方法；文献[3]利用区间AHP形成综合效益评分，然后通过区间0/1规划进行再分配求解。AHP虽然能够将决策者的主观印象定量化，但是由于受决策者的主观判断影响，不确定性因素较多。2）以客观数据为基础的评估方法（下文简称客观评价法），主要代表为数据包络法（DEA）。韦钢等人于2007年利用超效率DEA应用于电网规划，主要思想是把指标定量化，并归纳为输入和输出两类；文献[5]在此基础上融合了交叉概率模型对DEA进行了改进。DEA虽然是一种客观方法并且无需考虑各指标的权重，但是把指标分为输入和输出来评价决策单元的有效性，由于输入和输出指标联系性不大，因此不能完全地体现各方案的优势性。另外，忽视了决策者在电网规划中的重要性。同时，这两类方法容错性能不好，当决策者判断失误，或者客观数据错误时将带来不可估量的后果。

基于上述分析，本文提出了能体现决策者主观判断并且能够考虑客观数据的方法—AHP和DEA相融合的方法。在此基础上，笔者提出了两种方法—带有灰色关联度和不带有灰色关联度的模型。灰色关联度是利用各方案与最优方案之间的关联度来对方案排序的方法，已广泛应用于工业生产生活中。在不带有灰色关联度的方法中，决策者通过AHP分析各种指标权重，然后利用DEA分析各指标中的数据。在带有灰色关联度的方法中，利用AHP和DEA共同决定指标的权重，然后利用灰色关联度计算各方案与最优方案之间的关联度大小评估电网规划方案。

1 电网规划综合评价指标

由于电网规划是一个复杂多变、目标众多、不确定因素较大的非线性决策过程。因此，要评价一个电网规划方案是否合理，必须建立一个与方案相关的指标因素。这些因素主要包括：可靠性指标、经济性指标、占地和环境指标以及适应性指标。其中各指标因素又分成若干个指标，为便于统计，将电网规划综合评价指标以层次结构的形式展现，具体见图1。图中各关系通过树的形式呈现，最终确定21个树叶属性因素作为全面评价电网规划方案的指标。

图1 电网规划方案指标集体系

2 基于AHP-DEA的综合评价模型

2.1层次分析法

层次分析法是一种定性分析与定量分析相结合的多目标决策分析方法。其基本原理是首先将决策问题的组成因素按支配关系形成递阶的层次结构；然后，专家依据一定标度对各元素之间的相对重要性进行打分评判，使专家的主观意见客观化；其次，此基础上构造出判断矩阵；最后，通过判断矩阵计算出各元素指标的权重系数。具体步骤如下。

1）建立层次结构模型

将决策的目标、准则和对象按它们之间的相互关系分为最高层、中间层和最低层，建立层次结构图。

2）构造判断矩阵

针对上一层的某个因素，确定本层所有因素的相对重要性的比较，文中采用1-9标度法（具体见表1）对重要性判断结果进行量化。

3）计算各因素权重

文中采用几何平均近似法（方根法）计算判断矩阵的最大特征值和对应的特征向量。

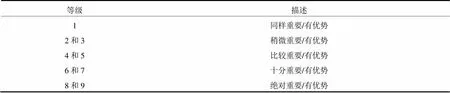
表1 评判标准

(2)

④计算判断矩阵的最大特征值

4）判断矩阵的一致性检验

①计算判断矩阵的一致性

其中，=0表示完全一致，越大，判断矩阵的一致性越差。

②设定平均随机一致性指标

对于1～9阶矩阵，平均随机性一致性指标如表2。

表2 平均随机性一致性指标

③计算随机一致性比率

2.2数据包络法

数据包络法（DEA）是一种直接使用输入、输出数据建立非参数的线形规划数学模型。它是以决策单元中的输入和输出数据的权重作为变量，从最有利于决策的角度进行综合评价，以便确定各决策单元是否为DEA有效。其中模型是DEA中运用最广泛的模型之一。其基本思想是：设有个决策单元DMU，每个决策单元DMU有个输入指标和个输出指标，则对应的输入量和输出量分别为和，且有和。另外，设输入量对应的输入权重为和输出量对应的输出权重为。现针对第个决策单元DMU进行效率评估，以第个决策单元的效率指数为目标，以所有决策单元的效率指数为约束，可建立一个分式规划的优化模型，引入剩余变量和松弛变量以及非阿基米德无穷小量，利用对偶规划进行Charnes-Cooper变换，则可得到以下线性规划模型。但是，在实际评价过程中，当评价多个决策单元时很可能出现多个决策单元同时有效，从而无法对决策单元做出有效判断。基于此，通过Per Andersen等人提出的一种DEA的超效率（Super Efficiency SE-DEA）模型，可以有效地对决策单元进行排序，其基本思想是当评价某决策单元时，把该决策单元排出在集合之外，其表达式为

(8)

2.3 AHP-DEA评价模型

针对上述的AHP和DEA方法不难看出，AHP评价方法受决策者主观影响较大，是一种非定量的主观评价方法。DEA虽然是一种客观的评价工具，但是它只受输入和输出指标影响，没有考虑实际因素的影响，不具有全面性。基于此，笔者综合这两个模型的优势，提出了两种AHP-DEA的多目标优化的主客观相结合评价模型。即不带有灰色关联的AHP-DEA模型和带有灰色关联的AHP-DEA模型。

2.3.1 不带灰色关联的AHP-DEA模型

该方法基本思想是通过AHP计算电网规划中的一层指标（技术性指标、经济性指标、占地和环境指标、适应性指标）对总目标的权重，然后结合DEA分析各一级指标的超效率值。

① 基于AHP计算技术性指标、经济性指标、占地和环境指标以及适应性指标对总目标的权重为、、和，写成向量形式为。

② 所有指标按技术性指标、经济性指标、占地和环境指标以及适应性指标分类形成评价集合，并把各个评价集合中的下一层指标分成输入指标和输出指标通过超效率DEA计算各一层指标的超效率值为、、和，写成向量形式为。

③ 利用①中的权重和②中的超效率计算总体效率值为

2.3.2 带有灰色关联的AHP-DEA模型

带有灰色关联的综合模型通过确定各方案与最优方案之间的关联度来评价方案的优劣，可提高各方案的可区分度。

① 利用AHP求出底层指标（文中电网规划的底层指标共有21个子指标）对总目标的权重为；

② 把21个底层指标分为输入（10个指标）和输出（11个指标）两类，通过超效率DEA求出不同方案下的剩余变量和松弛变量，则第个方案的剩余变量和松弛变量的向量为，对进行归一化处理为。

(11)

⑤ 对方案集矩阵进行规范化处理，由于各指标之间的量纲和数量级不同，无法直接比较，依据本文电网规划数据的特点，各数据之间相差较大，笔者选择Z-score方法进行数据标准化，设、分别为中第列元素的平均值和标准差，则中某元素以及规范化为

(13)

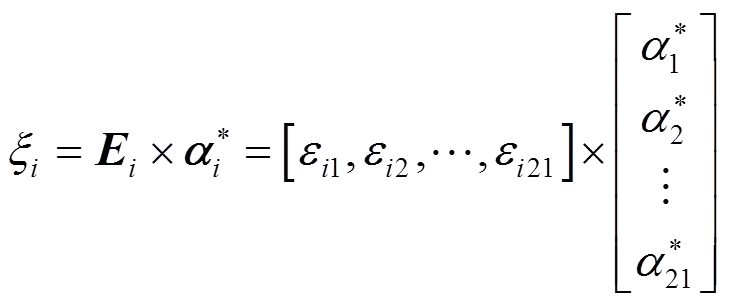
3 实例分析

3.1 实例

为了验证模型的合理性，对其实际电网进行综合规划。某规划区的配电网规划如下：高压配电网规划范围为面积为62 km的全区、中压配电网规划范围：面积为7.43 km的核心区以及面积为2.4 km的新镇一区。经过筛选比较，最终确定三个最具代表性的方案：35 kV方案（方案1）、110 kV方案（方案2）以及35 kV和110 kV混合方案（方案3）。各方案的实际情况和具体数据见表3，其中带“*”的为输入指标，处理方法见文献[4]，本文不再赘述。表中的数据均为处理后的数据，其中把“越小越优”的指标确定为输入指标，“越大越优”的指标确定为输出指标。

3.2实验结果分析

表4为利用本文案例通过不同方法计算的3个电网规划方案的实际权重以及排序。

由表可知：和文献[7]中的方法无法排序以及文献[8]的最优方案与其它不同，不难发现，分析可知三种方法在运用进行有效性判断时，出现了多个决策单元同时有效，从而弱化了DEA的作用。本文方法的最优方案为方案三，与SE-DEA、AHP、文献[1]的模糊层次分析法和文献[2]的区间层次分析法得的结果一致。实际规划中，方案三也是首选方案。

表3 各方案的输入数据

表4 各方法决策结果

虽然SE-DEA、AHP、模糊层次分析法和区间层次分析法都取得了一致结果，但是AHP、模糊层次分析法和区间层次分析法完全是由决策者的主观设定，通过决策者的主观偏好建立判断矩阵，存在不可忽视的主观不确定因素。SE-DEA是一种只受输入和输出数据影响的评价方法，完全忽视了决策者实际偏好。本文两种算法充分利用了两种方法的优势，通过AHP和DEA共同决定决策方案的最终权重，从而有效地考察电网规划方案。

3.3容错性能分析

在实际情况中，方案的决策受到众多因素的影响。因此，会出现某些数据真实性不强或人为干预的状况，在这种极端非正常的情况下各评估方法是否能够得到正确的结果体现了算法的容错性能和实用性能。在主观评价法中某决策者出现非正常判断性失误时，例如，电网规划中占地与环境指标遭到人为因素的干预，使得为了追求技术和经济的最大化，忽略了占地与环境的重要，得到的结果如表5。

表5 主观评价方法的容错性能

通过表5分析可知，当遭到非正常干预时，本文方法1—不带灰色关联度的AHP-DEA和AHP具有较差的容错性能，而本文方法2—带灰色关联度的AHP-DEA具有较强的容错性，在非正常情况下都能得到理想结果。

在客观评价中，如果某一输入数据错误，例如各地区站点浪费情况输入错误，变成0.000 01时，结果如表6。

表6 客观评价方法容错性能

通过表6分析可知：带灰色关联度的AHP-DEA相比其他算法具有较强的容错性。因此，不难得出结论本文方法二出现错误数据干扰时，仍能够筛选出合理的规划方案。

4 结论

本文提出了两种AHP-DEA方法应用于电网规划综合评判中，取得了较好的效果。方法巧妙地结合了AHP和DEA的优点，有效地弥补了AHP主观性过强和DEA不能反映决策者偏好的缺陷。另外，文中的方法二融合了灰色关联度提高了各方案的可区分度，并且相对于其他方法具有较强的容错性能，因此，在电网规划中具有广泛的运用前景。

[1] 陈大宇, 肖峻, 王成山. 基于模糊层次分析法的城市电网规划综合评判[J]. 东北电力技术, 2003(9): 5-14.

CHEN Da-yu, XIAO Jun, WANGCheng-shan. Comprehensive judgment of policy-making for urban power network based on fuzzy analytic hierarchy process[J]. Northeast Electric Power Technology, 2003(9): 5-14.

[2] 肖峻, 王成山, 周敏. 基于区间层次分析法的城市电网规划综合评判决策[J]. 中国电机工程学报, 2004, 24(4): 50-57.

XIAO Jun, WANG Cheng-shan, ZHOU Min. An IAHP-based MADM method in urban power system planning[J]. Proceedings of the CSEE, 2004, 24(4): 50-57.

[3] 肖峻, 罗凤章, 王成山. 一种基于区间分析的电网规划项目决策方法[J]. 电网技术, 2004, 28(7): 62-67.

XIAO Jun, LUO Feng-zhang, WANG Cheng-shan. An interval-based method for evaluation and decision-making of power system planning projects[J]. Power System Technology, 2004, 28(7): 62-67.

[4] 韦钢, 吴伟力, 刘佳, 等.基于SE-DEA 模型的电网规划方案综合决策体系[J]. 电网技术, 2007, 31(24): 12-14.

WEI Gang, WU Wei-li, LIU Jia, et al. Comprehensive judgment for power system planning alternatives based on SE-DEA model[J]. Power System Technology, 2007, 31(24): 12-14.

[5] 高庆敏, 张乾业.基于 SE-DEA 的交叉效率模型的城市电网规划综合评判决策[J]. 电力系统保护与控制, 2011, 39(8): 60-64.

GAO Qing-min, ZHANG Qian-ye. Comprehensive evaluation and decision-making for urban power system planning using a cross efficiency model based on SE-DEA[J]. Power System Protection and Control, 2011, 39(8): 60-64.

[6] 王先甲, 张熠. 基于AHP和DEA的非均一化灰色关联方法[J]. 系统工程理论与实践, 2011, 31(7): 1221-1229.

WANG Xian-jia, ZHANG Yi. Non-uniform grey relational method based on AHP and DEA[J]. Systems Engineering-Theory & Practice, 2011, 31(7): 1221-1229.

[7] 杨德权, 裴金英. 基于DEA-AHP的物流系统绩效评价研究[J]. 运筹与管理, 2009, 18(5): 81-86.

YANG De-quan, PEI Jin-ying. Study on logistics performance evaluation based on DEA-AHP method[J]. Operations Research and Management Science, 2009, 18(5): 81-86.

[8] DENG J L. Control problems of grey systems[J]. System &ControlLetters, 1982, 1(5): 288-294.

[9] 李如琦, 唐林权, 凌武能, 等. 基于前景理论和灰色关联分析法的黑启动方案优选[J]. 电力系统保护与控制, 2013, 41(5): 103-107.

LI Ru-qi, TANG Lin-quan, LING Wu-neng, et al. Optimization of black-start based on prospect theory and grey relational analysis[J].Power System Protection and Control, 2013, 41(5): 103-107.

[10] 马丽叶, 卢志刚, 常磊, 等. 基于灰色关联度的输电网经济运行指标体系研究[J]. 电力系统保护与控制, 2011, 39(12): 22-26.

MA Li-ye, LU Zhi-gang, CHANG Lei, et al. Study of index system of economic operation of grid based on gray correlationdegree[J]. Power System Protection and Control, 2011, 39(12): 22-26.

[11] 万卫, 王淳, 程虹, 等. 电网评价指标体系的初步框架[J]. 电力系统保护与控制, 2008, 36(27): 14-18.

WAN Wei, WANG Chun, CHENG Hong, et al. Preliminaryframe of index system for evaluating power network[J]. Power System Protection and Control, 2008, 36(27): 14-18.

[12] 李正明, 张纪华, 陈敏洁. 基于层次分析法的企业有序用电模糊综合评估[J]. 电力系统保护与控制,2013, 41(5): 136-141.

LI Zheng-ming, ZHANG Ji-hua, CHEN Min-jie. Fuzzy comprehensive evaluation of enterprise’s orderly power utility based on analytic hierarchy process[J]. Power System Protection and Control,2013, 41(5): 136-141.

[13] 李金超, 李金颖, 牛东晓, 等. 基于ANP的电网企业运营能力评价模型研究[J]. 电力系统保护与控制,2011, 39(19): 37-43.

LI Jin-chao, LI Jin-ying, NIU Dong-xiao, et al. Study on the evaluation model for the power grid corporation operation ability based on ANP[J]. Power System Protection and Control, 2011, 39(19): 37-43.

[14] 李晓辉, 张来, 李小宇, 等. 基于层次分析法的现状电网评估方法研究[J]. 电力系统保护与控制, 2008, 36(14): 57-61.

LI Xiao-hui, ZHANG Lai, LI Xiao-yu, et al. The research on the evaluation system for existing network based on analytic hierarchy process and Delphi method[J]. Power System Protection and Control, 2008, 36(14): 57-61.

[15] 朱乔. 数据包络分析(DEA)方法综述与展望[J]. 系统工程理论与方法用, 1994, 3(4): 1-8.

ZHU Qiao. Data envelopment analysis: a review and visions for future research[J]. Systems Engineering- Theory Methodology Application, 1994, 3(4): 1-8.

[16] 刘艳, 顾雪平, 张丹于. 数据包络分析模型的电力系统黑启动方案相对有效性评估[J]. 中国电机工程学报, 2006, 26(5): 32-37.

LIU Yan, GU Xue-ping, ZHANG Dan-yu. Data envelopment analysis based relative effectiveness assessment of power system black-start plans[J]. Proceedings of the CSEE, 2006, 26(5): 32-37.

[17] 罗道平, 肖笛. 数据包络分析(DEA)在电力工业的应用[J]. 系统工程理论与实践, 1996(4): 60-66.

LUO Dao-ping, XIAO Di. The application of data envelopment analysis (DEA) in electric power industry[J]. Systems Engineering-Theory & Practice, 1996(4): 60-66.

Comprehensive judgment for power system planning alternatives based on AHP-DEA

CHEN Kui, WEI Xiao-guang, NIU Jun-ping, CHEN Jing-bo

(School of Information and Electrical Engineering, China University of Mining & Technology, Xuzhou 221008, China)

Regarding the complexity of the judgment for power system planning alternatives and the fact that analytic hierarchy process (AHP) has the strong subjective and data envelopment analysis (DEA) can not reflect the preference of decision makers, a method integrating AHP and DEA is proposed. The method is divided into two models whether grey relational method is fused. Meanwhile, two models are applied to a practical power system planning problem by establishing an evaluation system for power planning. It is showed that the calculation result is consistent with the expected result. On the basis, the fault-tolerant for the models is analyzed. It is found that the fault-tolerant of the model with the grey relational method is better than other methods. When the abnormal factors affect power system planning, the model with the grey relational method can still choose the optimal plan.

power system planning; analytic hierarchy process (AHP); data envelopment analysis (DEA); grey relational method; supper efficiency; fault-tolerant

TM715

A

1674-3415(2014)21-0040-07

2013-12-22；

2014-09-02

陈 奎（1973-），男，博士，副教授，主要研究方向为电力系统继电保护；

韦晓广（1973-），男，通讯作者，硕士，主要研究方向为人工智能在电力系统中的应用和电网规划；E-mail: wei_xiaoguang@aliyun.com

牛俊萍（1986-），女，硕士，主要研究方向为电力系统谐波检测。