Savitzky-golay滤波在陀螺仪角加速度测量中的应用

雷 阳，门义双

（中国北方车辆研究所，北京 100072）

近年来，陀螺仪作为高精度伺服控制系统的反馈元件，用来反馈测量物体转动的角速度。但当控制系统进行高精度控制时，就需要测量反馈角加速度的数据值。目前，角加速度的测量方法有直接法和间接法两种[1]。为了系统不增加传感器，提高系统的可靠性，本文采用间接法，也就是利用系统原有的速率陀螺仪进行现场采样，采样得到的数字角速度信号数据再进行分析与微分处理来求得角加速度值。因此，对陀螺仪采集的速度数据处理是在实际工程系统设计应用中的一个重要的环节[2-3]。

然而，在震动环境下工作的陀螺仪所采集到的数据中干扰信号量比较大，微分运算对干扰量的放大严重影响了求解角加速度的准确性。所以陀螺仪采集到的数据必须要经过滤波处理才能微分求解。当精度要求不高时，系统可应用输出量为模拟信号的陀螺仪，输出的信号可以直接经过电容等硬件滤波的方法进行平滑处理。然而，随着控制精度的提高，系统应用于高精度的数字陀螺仪，尤其是光纤陀螺仪时，所输出的数字信号就无法硬件滤波，必须进行软件数字滤波的处理。目前，通常采用一般软件数字滤波方法，如算数平均滤波、限幅滤波、中值滤波和一阶滞后滤波对其测量数据进行处理，但滤波效果不是很理想。通过对多种滤波的实际计算结果进行了对比研究，提出了一种应用Savitzky-golay数值滤波来消除这些干扰信号的软件数子滤波方法，很好地解决了这个问题。

1 一般数字滤波数据处理的局限性

1.1 陀螺仪速度信号的采集与加速度的计算

对于实时性要求很高的伺服运动控制系统来说，需要每0.002 1 s采集一个速度信号值，来达到精确的位置控制，满足高精度的要求。然而，根据所采集到的速度信号求其所对应时刻的加速度值时，通常使用的是数值微分公式对实际测量到的原始速度数据进行数据处理。常用的数值微分公式有两点数值微分公式和三点数值微分公式。由于三点数值微分公式相对误差值小，因此使用三点数值微分公式对原始采样数据进行处理，以得到相应的加速度信号[4]。

1.2 一般数字滤波数据处理的局限性

在一般数据处理中，通过陀螺仪采样得到速度信号的原始数据，通过三点数值微分公式计算得到相应的加速度值，结果如图1所示。

从图1可以看出，用原始数据直接计算得到实时的加速度曲线出现了非常多的毛刺和跳跃。这是因为陀螺仪是在振动的环境下进行速度数据采集的。这些振动是难以避免的，这使得测量的数据偏移了实际数值。众所周知，加速度是速度的一阶导数，在采样时间周期为0.002 1 s这样非常小的数值时，对于速度的一个很小的扰动，都会对数据处理后的加速度数据产生很大的影响。从图1（b）就可以看出，不经过滤波处理计算得到的加速度曲线毛刺和跳跃很大，没有数据分析的价值。

目前在工程中，一般数字滤波方法主要有算数平均滤波、限幅滤波、中值滤波和一阶滞后滤波。分别运用这四种方法，首先对陀螺仪采集到的速度信号进行滤波，再应用三点数值微分公式进行加速度计算。正弦速度运动应用四种不同滤波方法得到的加速度波形如图2所示。其中，图 2（a）为 5点求取平均值方法的算数平均滤波后求得的角加速度波形图，图2（b）为最大偏差值为0.02方法的限幅滤波后求得的角加速度波形图，图2（c）为连续采样5次方法的中值滤波后求得的角加速度波形图，图 2（d）为滤波参数 a=0.2方法的一阶滞后滤波后求得的角加速度波形图。

从图2可以看出，算数平均滤波的方法较原始数据所求得角加速度的曲线图有所平滑，但是角加速度曲线的跳跃仍然很大，取得的效果不理想，而且降低了精度；限幅滤波的方法与中值滤波的方法应用效果不明显，毛刺以及跳跃均很大，数据分析价值不大；一阶滞后滤波的方法，虽然使角加速度的波形有所平滑，但由于滤波本身方法的限制，产生了相位的滞后，与系统其他数据时域相结合分析时造成了困难，不利于进一步的数据分析。

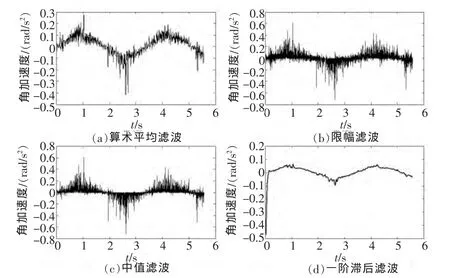
图2 滤波后微分得到的的角加速度曲线

综上所述，由于一般数字滤波数据处理中存在局限性，不能满足陀螺仪采集数据处理的要求。

2 基于Savitzky-golay滤波的数字滤波方法的设计实现

2.1 Savitzky-golay滤波原理[5-6]

SG滤波算法的主要思想是：通过取采集数据点xi附近固定个数的点拟合一个多项式，多项式在xi的值就给出了它的光滑数值 gi（gi∈G所求光滑数值矩阵）[7]。

以nl表示xi左边点的个数；以nr表示xi右边的点的个数；pi（x）表示相对于点 xi的一个 M次多项式，用它在最小二乘意义下拟合这nl+nr+1个点。因此：

根据实测数据 yi拟合 M次多项式 pi（x），可写成：

假设横坐标xi具有xi+1-xi≡△x的均匀间距，为在最小二乘意义下用 pi（x）拟合测试数据，必须准确确定系数 bk，使得：

分别定义矩阵A、B和Y：

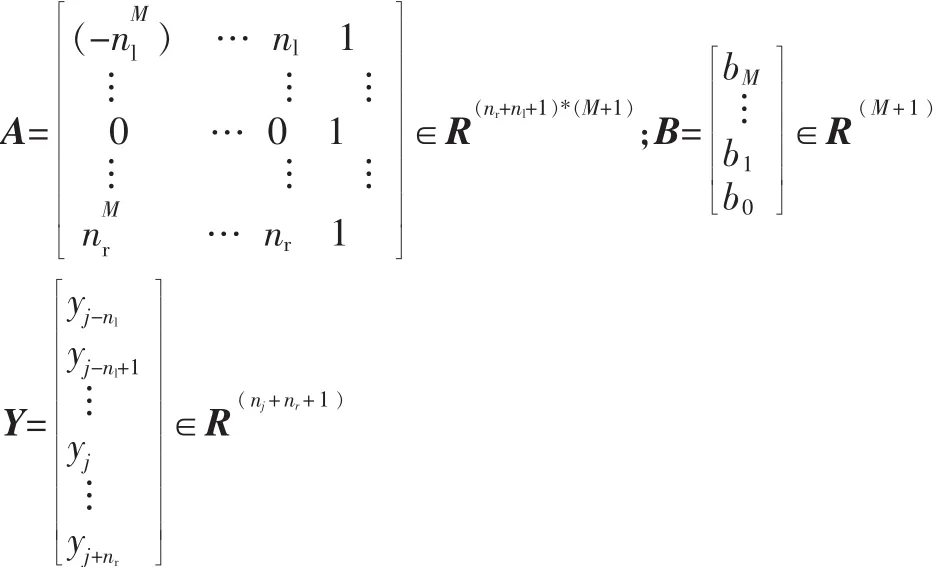
利用这些定义，就可以用矩阵形式进行表述此问题：

为求解 B，使得式（4）达到最优，令 AB=Y，左乘 AT方程变为：

根据式（5），则可以进一步求得：

因此，可得到矩阵 Y=A（ATA）-1ATY，则所求得光滑数值为

2.2 基于Savitzky-golay滤波的数字滤波方法的实现

通过滤波原理，可得出 nl和 nr越大，曲线的平滑性越好，不过这是以牺牲曲线特性为代价的；相反，M的取值越大，曲线特性失真率越低，但使得数据低频部分的平滑度降低，计算量也变大[8]。

本文通过对多组实测数据进行多个不同滤波参数处理后的综合比较，在满足确定失真率不大的情况下，尽可能地增加平滑性，最后选择出了所采用nl=nr=15、M=3的滤波参数。应用此参数，对陀螺仪采集的速度信号进行滤波，经过滤波后的波形以及滤波后求得的角加速度的波形图如图3所示。

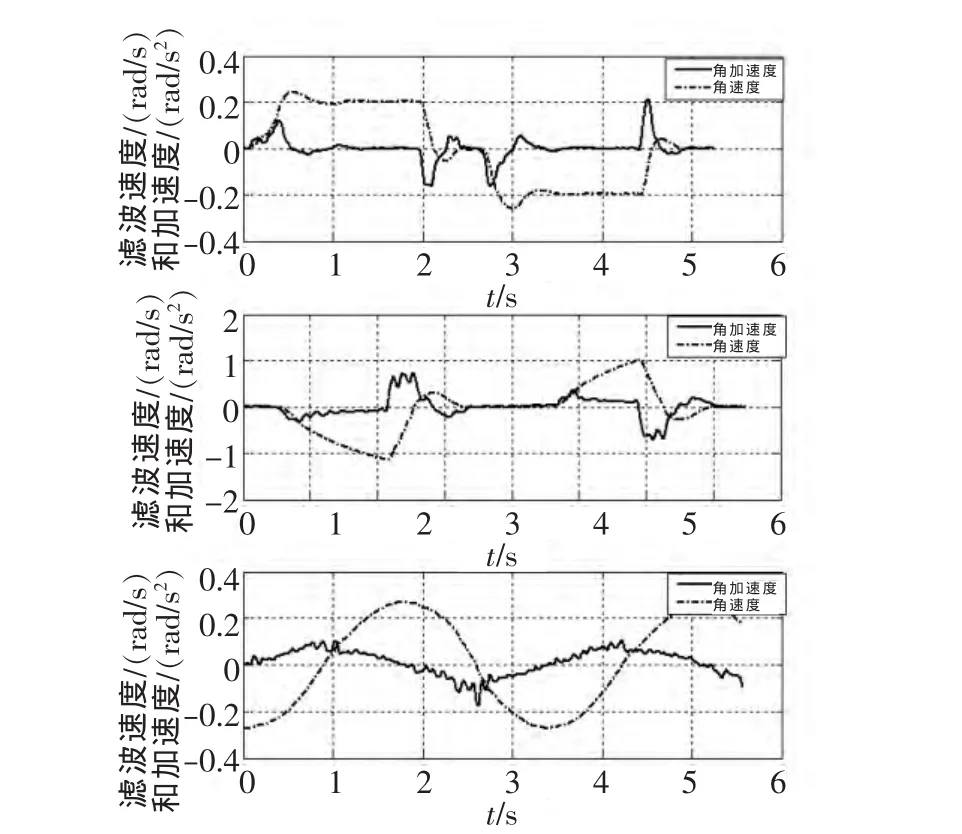
图3 Savitzky-golay滤波后求得的角加速度的波形图

下面选择采取 SSE（误差平方和）和 RMSE（标准差）的技术指标来评价在正弦速度运动的采集信号经不同种滤波方法处理后的滤波效果，如表1所示。

从图3、表1可以看出，原始数据经过Savitzky-golay滤波后数据得到了平滑，SSE值和RMSE值也越接近于0，有效地消除了毛刺，较好地保证了经过滤波后速度信号数据，并且依旧保留了信号的主要特征，消除了干扰信号。这样，对滤波后的速度信号再进行数据微分处理，得到的加速度曲线基本上消除了毛刺以及各种跳跃，而且没有时间滞后现象的发生，有利于对数据进行进一步处理，进而为设计高精度的控制系统提供了依据。

本文针对陀螺仪采集到的速度数据信号进行微分处理中遇到的问题，进行了采用不同滤波方法的分析与研究。提出了将Savitzky-golay滤波方法应用到此数据处理中，发现Savitzky-golay滤波方法在进行陀螺仪速度信号处理方面取得了较好的效果，而且此滤波方法是一种不受原始数据本身限制的低通平滑滤波算法，并不需计算滤波的截止频率。最后通过实际计算得到的滤波后的速度波形和加速度波形可以看出，Savitzsky-golay滤波方法较工程上的传统滤波方法在去噪效果和数据微分方面有了一定程度的改进。

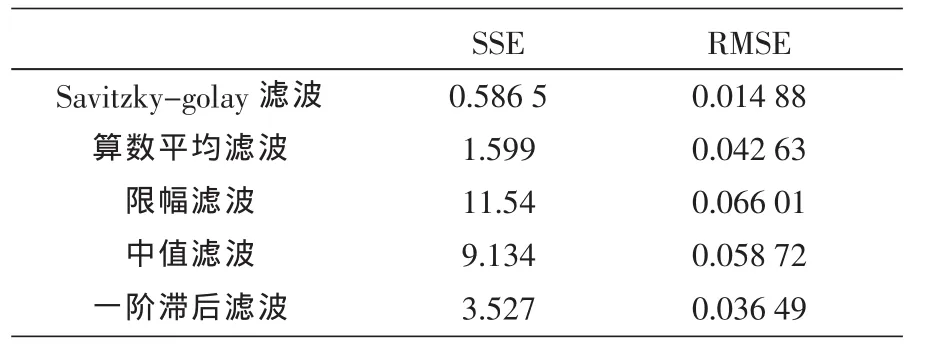
表1 滤波效果对比

[1]OVASKA S J， VALIVIITA S. Angular acceleration measurement：a review[J].IEEE Transactions on Instrumentation and Measurement， 1998，47（5）：1211-1217.

[2]卓斌.速度陀螺仪采样数据的分析研究[J].计算机测量与控制，2006，14（9）：1213-1215.

[3]ROMMANEE J， PIOTR P， VANJA G， et al.A method for dead reckoning parameter correction in pedestrian navigation system[J].IEEE Transactions on Instrumentation and Measurement， 2003，52（1）：209-215.

[4]李广华，张爱民，张杭，等.Savitzky-golay滤子在断路器在线检测数据处理中的应用 [J].高压电器，2005，41（3）：225-227.

[5]蔡天净，唐瀚.Savitzky-Golay平滑滤波器的最小二乘拟合原理综述[J].数字通讯，2011，01（017）：63-68.

[6]GANDER W， HREBIEEK J， BARTON S.Solving Problem in Scientific Computing Using Maple and Matlab[M].Berlin： Springer-verlag， 1993.

[7]桑庆双，程健.SG滤波在朗缪尔探针信号处理中的应用[J].计算机工程，2011，37（17）：220-226.

[8]PRICHARD D，THEILER J.Generating surrogate data for time series with several simultaneously measured variables[J].PhysicalReview Letters， 1994， 73（7）： 951-954.