LPC与LSF系数转换的FPGA实现

张 俏，杨 骁，汤 炜

（华侨大学 信息科学与工程学院，福建 厦门 361021）

线性预测法（LPC）成功地应用于语音信号处理的各个方面，在语音参数的估计中也被广泛地应用，如基音周期、共振峰频率和谱特征分析等。线性预测的基本思想是：由于语音信号之间存在相关性的特点，可以用过去若干个语音采样值或它们的线性组合近似表示当前语音采样值。在LPC分析中，最普遍的方法是使用线谱频率（LSF）表示LPC参量[1]。LSF是频域参数，具有良好的量化特性和内插特性，小系数的误差引起滤波器的局部误差，构成的合成滤波器有较好的稳定性[2]。10阶的LPC系数的LSF参数成功地应用在低速率语音编码器中，如混合激励线性预测（MELP）声码器。近几年，在语音信号处理中，LSF参数研究一直是热点，参考文献[3-4]对LSF参数量化方法进行分析与仿真，但由LPC系数与LSF系数相互转换的研究少之又少。

伴随语音技术的不断发展，对语音信号数字化处理的实时性要求越发严格，专用的语音信号处理芯片能满足语音信号实时性的要求，LPC与LSF转换是专用语音处理芯片的关键模块之一。MELP算法语音编码过程中，首先，把经过带宽扩展后的线性预测系数转为LSF系数；其次，LSF参数按最小间隔排序；最后，对排序后的LSF进行4级矢量量化。MELP算法解码过程中，由内插的LSF参数计算合成滤波器的系数，得到合成滤波器，激励信号经过合成滤波器得到合成语音。由于LSF参数的特性，保证了合成滤波器的稳定性[5]。LPC与LSF转换算法的FPGA实现对语音编码、语音合成等领域硬件实现至关重要。本文给出了LSF到LPC转换运算推导，并给出了算法的实现步骤。

1 转换算法原理

1.1 由LPC系数向LSF系数转换

本文针对LPC系数计算LSF系数的Chebyshev多项式求解法进行研究：

P阶线性预测滤波器函数为：

{ai}i=1，2，…，p为线性预测系数。预测系数 ai在最小均方误差准则下，由Durbin递推算法求解自相关方程得到[6]。

LSF[7]作为LPC系数的等价表现形式，可通过求解p+1阶对称多项式 P（z）和反对称多项式 Q（z）的共轭复根获得。其中p+1阶多项式表示如下：

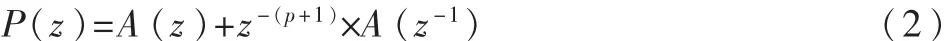
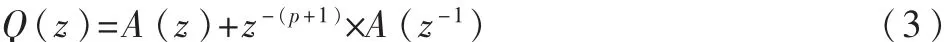
可以证明，当 A（z）的根位于单位圆内时，P（z）和Q（z）的根沿着单位圆相互交替出现。当p是偶数时，则P（z）有一个根 z=-1，Q（z）有一个根 z=1；当 p 为奇数时，Q（z）有±1 两个实根。设 P（z）的零点为 e±jωi，设 Q（z）的 零 点 为 e±jθi，则满足：0＜ω1＜θ1＜…ωp/1＜θp/1＜π。为计算方便，去掉与LSF系数无关的实根，得到两个新的多项式P′（z）和 Q′（z），当 p 为偶数时：

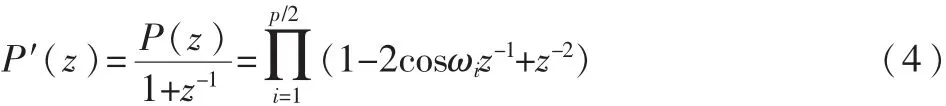
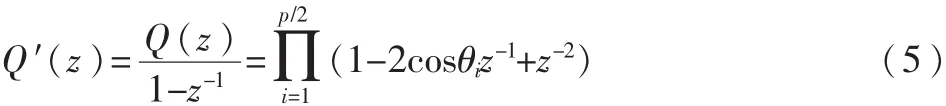
cosωi，cosθi，i=1，2，…，p，是余弦域的表示，ωi和 θi为P（z）和 Q（z）的第 i个零点，其中 ωi和 θi是成对出现的，反应信号的频谱特性，称之为“线谱对”，即要求的LSF参数。LSF系数可由切比雪夫多项式估计并在余弦域得到。可把 P′（z）和 Q′（z）写为：

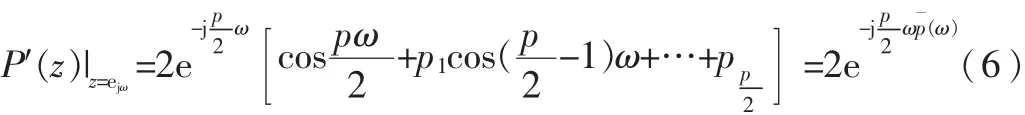
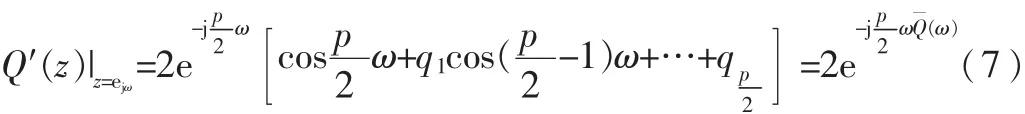
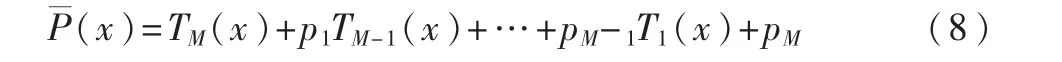
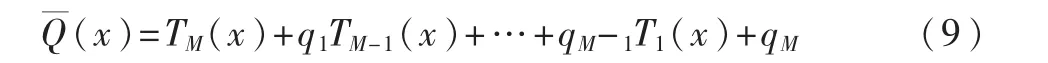
Chebyshev多项式求解法本质是求解x满足区间[-1，1]，求（x）=0 和（x）=0 的根{xi}，对应的 LSF 系数由ωi=arccosxi确定。

1.2 由LSF系数向LPC系数转换

在语音解码过程中，需要把量化和内插后的LSF系数转换回 LPC系数{ai}i=1，2，…，p，逆向推导，已知内插的 LSP 系数 fi，根据 fi可计算出 P′（z）和 Q′（z）的系数 p′i和 q′i。

其中 f2i-1=cosω2i-1，求出 p′i和 q′i。 根据原来方程式对应关系：

最后得到 LPC 系数可由 A（z）+P（z）+Q（z）/2 得到参数ai。

2 FPGA实现架构

2.1 算法实现步骤

量化和内插后的LSP系数需要更换成LPC系数ai。已知量化和内插的 LSP 系数 qi，i=0，1，…，p-1，根据前文推导，可以得到下面迭代公式：

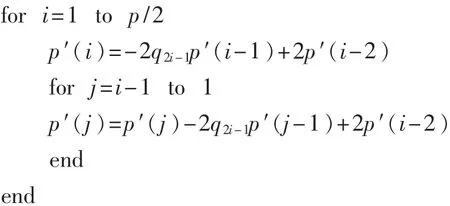
公式中的qi=coswi，余弦是通过查找表方式求得的，迭代过程中的初始值 p′（0）=1，p′（-1）=0。 上面迭代公式给出的是 p′（i）的求法，在求解 q′（i）时将上面的迭代公式中的q2i-1换成q2i即可。

在求得 p′（i）和 q′（i）后就可以求得 p（i）、q（i），求解公式如下：

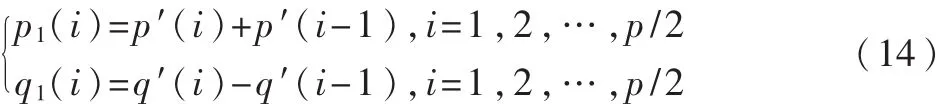
最后得到LPC系数：

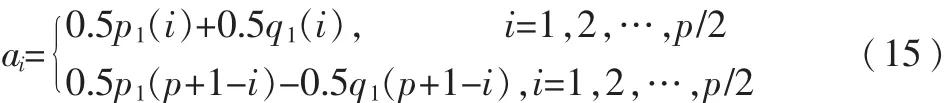
2.2 余弦信号发生器

FPGA实现LSP到LPC转换是通过上文介绍的迭代算法来实现的。因为qi=coswi，迭代过程中qi的值是根据wi值来求出的。对于余弦的计算有很多方法，CORDIC旋转是一种方法，查找表也是一种方法。CORDIC旋转方法通过数学函数逼近的原理，每次旋转一定的角度来得到余弦值，但是这种方法得到的精度和迭代的次数有关；查找表方法是先将余弦值根据量化位数计算出来存在ROM中，每次计算是需要将数据进行量化然后去ROM中查找量化值所对应的余弦值，这种方法计算速度快，但是存在一定的量化误差，会消耗一定存储空间。考虑到实时性语言编解码，本文的设计方案选择的是查找表法，在每一轮计算中通过wi值查找ROM来得到qi，借助DDS算法原理[8]，用相位累加器输出的数据作为波形存储器（ROM）的相位取样地址，这样就可以把存储在波形存储器内的波形抽样值（二进制编码）经查找表查出，完成相位到幅值的转变。

凭借MATLAB软件可以生成ROM中余弦波形的定点数值，共分3步完成。

（1）运用MATLAB计算出余弦波形浮点值，对其进行量化，生成定点数值。

（2）产生 mif文件（Altera FPGA ROM初始化数据文件格式）。

[1]苏新宁.数据仓库和数据挖掘[M].北京：清华大学出版社，2006.

[2]蒋盛益.数据挖掘原理与实践[M].北京：电子工业出版社，2011.

[3]罗雨滋，赵鹏起.改进的ID3算法在学生综合技能评估中的应用研究[J].佳木斯：佳木斯大学学报，2013（4）：80-82.