基于性能衰退的多态制造系统可靠性分析

周丰旭，李爱平，谢 楠，徐立云，邵 焕

（1．同济大学 现代制造技术研究所，上海 201804；2．同济大学 中德工程学院，上海 201804）

0 引言

可靠性是指产品在规定的条件下和规定的时间内，完成规定功能的能力［1］，它是产品质量的重要指标之一。对于价格高昂、结构复杂的机械系统，具有高可靠性是系统可靠运作、避免造成巨大经济损失和人身事故的重要保证。传统的可靠性分析方法往往把系统状态简化为“二元状态”（完全可靠和完全失效）。而实际生产中，系统从完全可靠衰退至完全失效会经历多种状态，称这种系统为多态系统［2－3］。多态系统于20世纪70年代提出，80年代初步建立了多态系统的相关理论。随着理论研究的深入，系统的多态性为可靠性理论的发展提出了新要求。

目前，国内外学者对多态系统可靠性理论的研究已取得一定成果。对于可靠性建模方法的研究，吴军等［4］探讨了运用数控装备使用过程中的性能劣化数据对数控装备可靠性进行预测的方法与工具，给出了基于性能状态监测的性能劣化建模与可靠性预测原理。王灵芝等［5］分析了生产设备各单部件最优的预防性维修策略，建立了以可靠性为中心的多部件系统预防性维修费用的优化模型。周金宇等［6］基于载荷离散化方法和概率发生函数建立了多状态系统可靠性定量评估模型，新模型可反映在失效共因下元件部分失效及其累积效应对系统各级性能的影响。刘宇［7］提出了模糊多状态复杂系统可靠性建模理论以及模糊多状态元件的更换维修决策方法。张均一［8］分别采用广义随机Petri网以及扩展随机Petri网对制造系统进行了模块化建模。针对可靠性分析策略，冯虎田等［9］讨论了强理智多态系统可靠性的特征量及评价指标，给出了强理智多态串联及并联系统可靠度计算表达式。Gregory Levitin等［10］利用可靠性框图和通用生成函数相结合的方法，分析了多态系统中故障传递对系统性能的影响规律。Suprasad等［11］采用多值决策图对多态系统失效概率进行了分析。Sharma等［12］利用实数编码遗传算法和模糊λ－τ算法研究了多态机器人系统的故障率、修复时间等各项可靠性参数，对多态机器人系统进行了可靠性分析和预测。李春洋等［13］针对具有多性能参数的多态系统可靠性分析的需要，提出了向量通用生成函数的定义和对应的运算符，并对系统的可靠度进行了评估。

以上文献的研究，要么假设故障后的系统经维修后可恢复至全新状态，要么只分析系统在运行过程中的两种状态（正常工作和失效状态）。对制造系统的深入研究表明，系统性能水平会随着使用和维修而逐渐衰退，且衰退速度随着维修次数的增加而加快。如果将维修后的系统简单地视为全新状态进行系统可靠性分析，或只研究系统维修后的两种状态，则会造成与实际情况有较大偏差。因此，建立制造系统性能衰退过程的数学模型，分析系统性能衰退规律对可靠性的影响，更加具有实际应用价值。

考虑到制造系统在性能衰退过程中的状态变化规律与时间间隔的起始时刻相关，本文运用非时齐Markov理论，在考虑系统非修复如新的前提下，建立可修机床性能衰退过程的多态模型，由机床到系统进行层级分析，探讨衰退现象对制造系统可靠性的影响规律。

1 问题描述

现代制造业中，复杂制造系统一般由若干个独立制造单元通过不同的方式组合而成。制造单元在工作过程中常常会因使用、磨损等发生老化衰退甚至失效等现象。制造单元失效后，虽可得到及时维修，但无论如何都不可能使其性能恢复至全新状态。随着工作时间的积累和维修次数的增加，会逐渐呈现老化状况，同时由最佳性能状态衰退至最差性能状态的速度也越来越快，整个系统性能也随之呈现出不同的状态。对其进行可靠性分析，研究性能衰退规律对可靠度的影响，可为将来寻找最佳维修方案提供依据。

为研究问题的方便，并为后续的模型分析提供依据，提出以下假设：

（1）制造系统为可修系统，系统中各单元失效后均可及时得到维修，维修后均能恢复至最佳的性能状态km，但并非全新状态。此时，整个系统也将恢复至其最佳的性能状态。

（2）对于整个系统而言，认为实际性能水平与任务性能水平相比较低时系统失效，并立即进行维修。

（3）进行可靠性分析时，只考虑因机床使用和磨损产生的退化失效，不考虑其他因素。

（4）组成系统的各单元寿命分布，以及其他出现的有关分布均为指数分布，且所有与这些分布有关的随机变量都相互独立。

对大型复杂制造系统进行可靠性分析时，如果直接对其进行建模求解，会导致状态维数的灾难现象，使计算的复杂程度成倍增加。根据随机过程原理建立机床在性能退化过程中的Markov模型，分析不同状态下机床的概率分布情况，再利用通用发生函数（Universal Generating Function，UGF）法结合层次分析法，推算出系统和子系统所对应的发生函数，可降低对多态制造系统进行可靠性分析的复杂程度。

2 单机床系统性能退化过程的Markov模型

假设系统由一台机床m组成，对系统的性能退化过程进行建模与可靠性分析，只需分析机床m即可。在m工作的过程中，往往因某些零件失效而使其性能发生变化，因此有必要对失效零件进行及时维修。根据Markov更新过程，随着维修次数的增加，机床由最佳性能状态衰退至最差性能状态的速度越来越快，换句话说，在下一个维修周期内，机床的状态转移率会按比例增加，定义该随机过程为｛Xm（t），t≥0｝。机床在第一个维修周期内的状态转移过程如图1所示。其中，状态km为机床m的最佳性能状态，状态0为机床m 的最差性能状态，ηm（ij）（t）表示机床m 从任意的较好性能状态i∈［1，…，km］转移到较差性能状态j∈［0，…，km－1］的转移率，这里i＞j。

机床m的瞬时状态转移矩阵

机床的状态概率为

任意状态i和状态j之间的转移率为

3 单机床系统性能退化过程的状态分析

定义机床m的性能为Gm（t），假设机床的性能分布区间为［0，km］，将机床分为km＋1个状态，由非时齐Markov理论［14］可得，t时刻m机床的各状态概率如下：

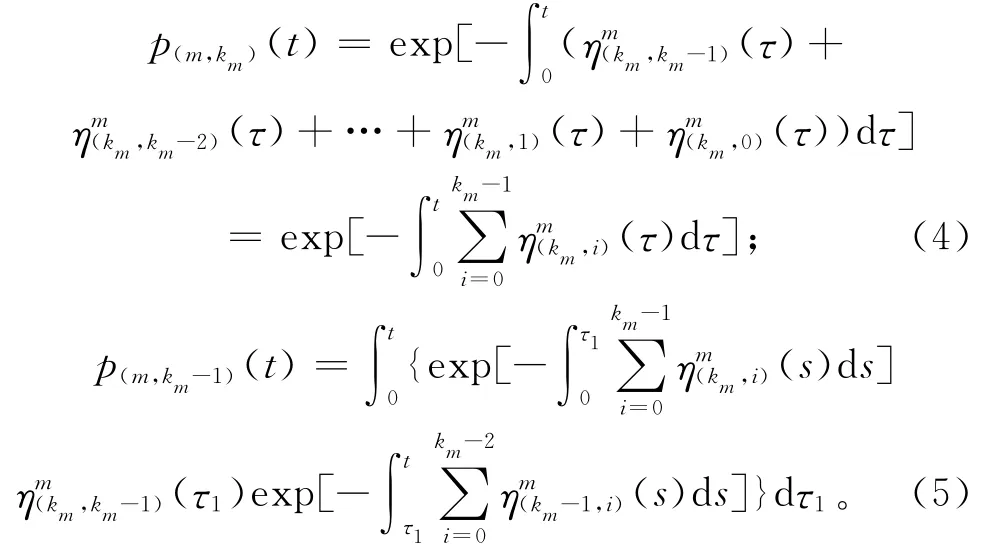
机床m处于km－2的状态概率与km－1状态相比，更加复杂。因为机床从最高性能状态km衰退至km－1时只有一种途径，即km，km－1，而机床从km状态衰退至km－2状态时有两种途径，分别为：和机床处于km－2状态的概率应为以上两种途径的概率之和，即

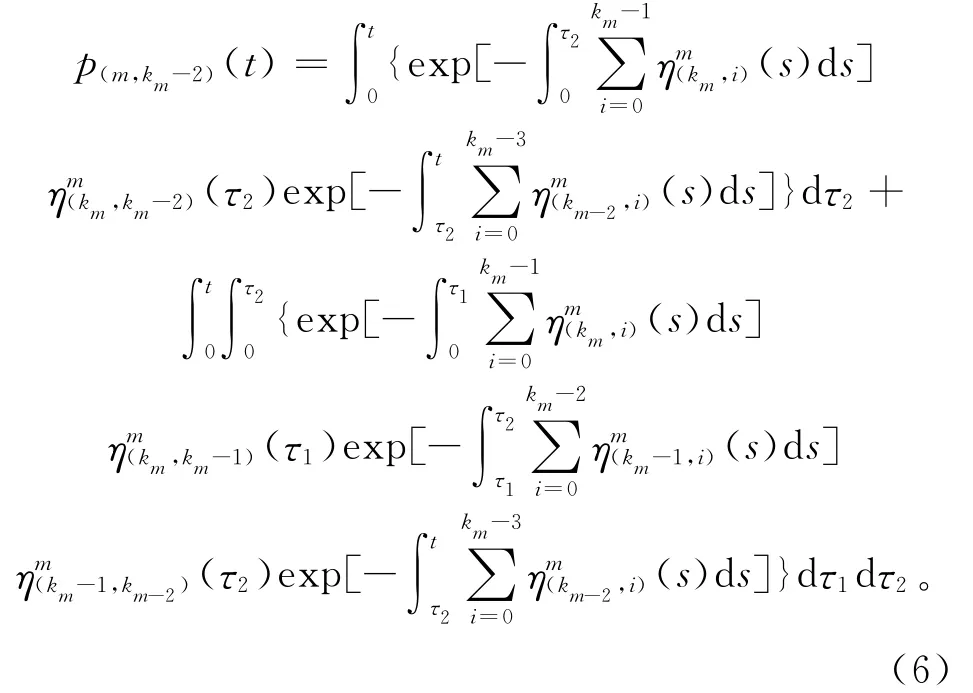
以此类推，机床m处于任意状态i的概率

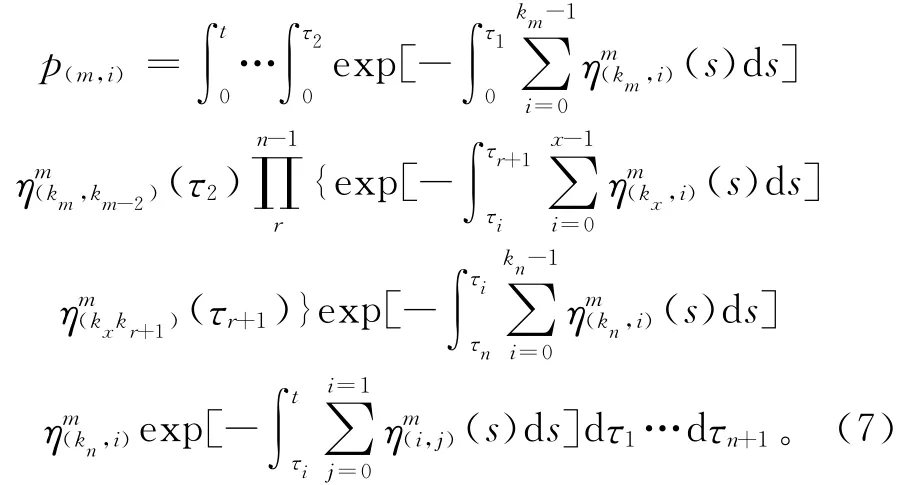
式中：n为从状态km到i所需要经过的中间状态数；kn为km－1，…，i＋1；r为1，2，…，n。

在机械制造系统中，往往只考虑稳定状态，假设机床m在t＝0时刻处于全新状态km，p（m，km）（0）＝1，p（m，km－1）（0）＝0，p（m，km－2）（0）＝0，…，p（m，0）（0）＝0为（t）＝1，即可求得机床在各个状态下的稳态概率。

表1是多状态机床m不同性能取值时的稳态概率，结合UGF法，可得出机床m的发生函数

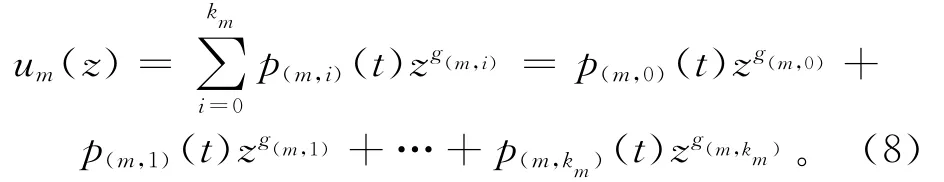
表1_机床m不同性能取值时的稳态概率

与二态元件不同，性能退化型机床的功能无法仅用“正常工作”和“失效”两种状态的属性进行描述，而是通过机床的某个可测量的性能指标来说明，这个性能指标的大小可反映任务性能水平的高低。初始条件，且各状态概率满足全概率条件当退化量为时间的单调递增函数时，与之相关的实效判断依据为：当性能水平降低到任务性能水平时，机床就处于失效的临界状态。

4 非串行多态系统可靠性分析

4．1 多态系统多级结构层级划分

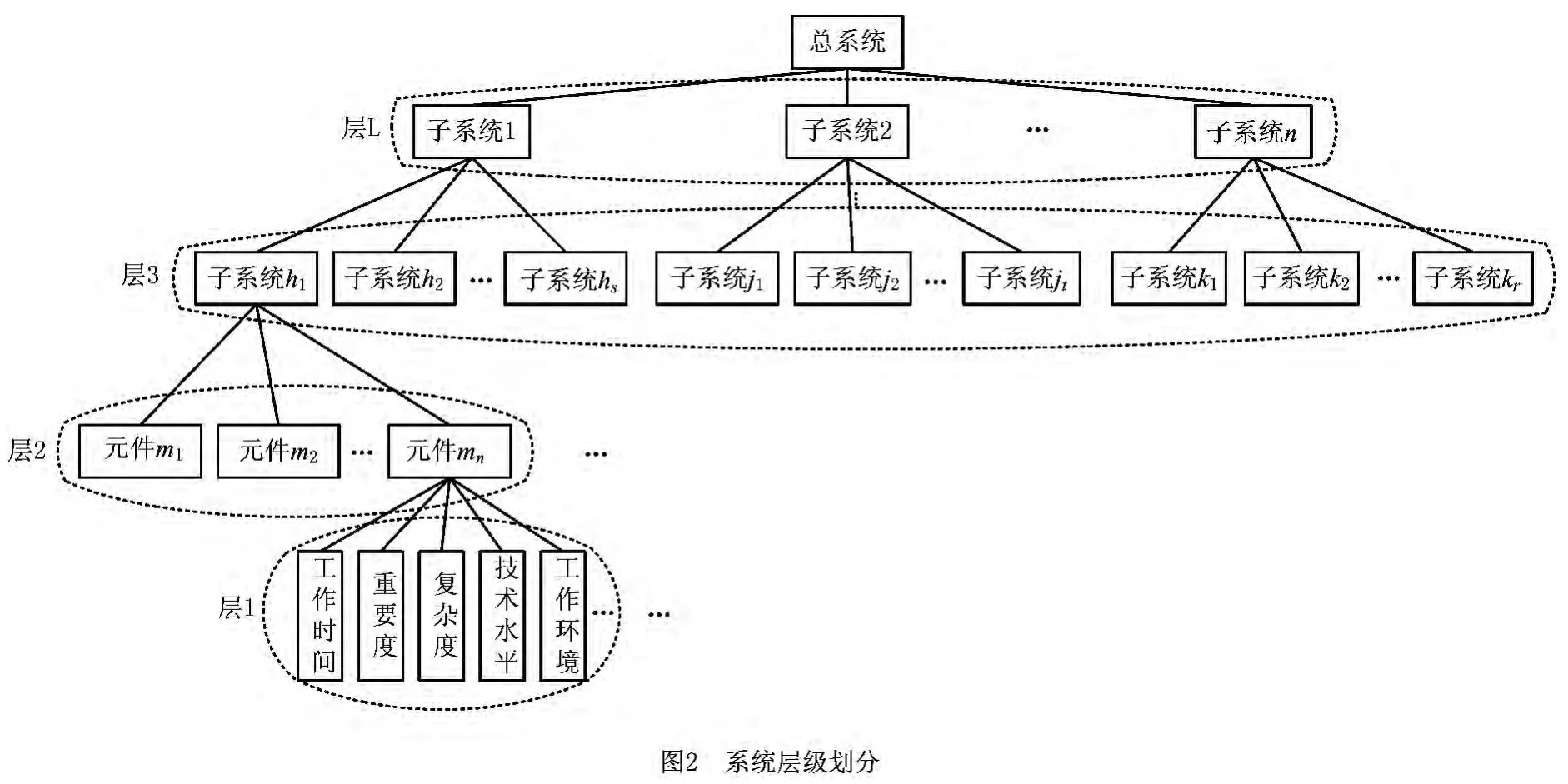
在对单机床系统（Single Machine System，SMS）状态分析的基础上分析Non－SMS的可靠性，还必须得到各机床与子系统、子系统与总系统的性能状态之间的关系。通过对非串行多态系统（Non－Serial Multistate System，Non－SMS）结构的深入分析发现，系统虽复杂但带有明显的层次性。为此，根据系统和子系统的层级关系和子系统在每一层级的权重，对整个系统结构进行层级划分，如图2所示。图2中，总的系统被分成L层，第L层可分为n个子系统，该层中的子系统n又可分为第L－1层中的子系统1，子系统2，…，子系统q，第3层中的子系统h1又分为第2层中的元件m1，元件m2，…，元件mn。对于层2的元件mn进行性能分析时，要同时考虑工作时间、重要度、复杂度、技术水平和工作环境等因素。运用模糊集理论，结合模糊层次分析法，依据不同领域专家的知识来确定影响因素的权重，从而可以得到真实、客观的评价结果［15］。一个由多个层级组成的性能衰退多态系统，如果各层级影响性能衰退的因素相对权重可以确定，则利用层级分析法再结合UGF法，就可以得到系统的性能可靠性。图2中，mn包含k个下级指标，即mn＝｛m，m，…，m｝，其中，第i个子集评价矩阵m

n1n2nkni＝［mni1，mni2，…，mni］，i＝1，2，…，k，这里，mni（i＝

jj1，2，…，k）表示指标mn的第i个下级指标相对于评定等级的隶属度。综上分析，指标mn的模糊关系矩阵

对模糊关系矩阵作归一化处理，可得模糊评价矩阵及各指标的权重集。在此基础上，定义第L层子系统n的性能状态为该子系统在第L－1层中所有子系统总的性能状态与子系统n相对于第L层中其他子系统的权重之积，即

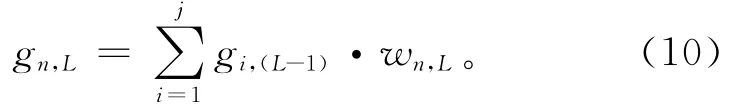
式中：gn，L，gi，（L－1）和 wn，L分别表示第L 层中子系统n的性能状态，第L－1层中子系统i的性能状态和子系统n相对于第L层中其他子系统的权重。

4．2 基于UGF法的系统可靠性分析

UGF是解决多态系统可靠性问题的有效途径。第一层中元件mn的发生函数可用如下多项式表示：

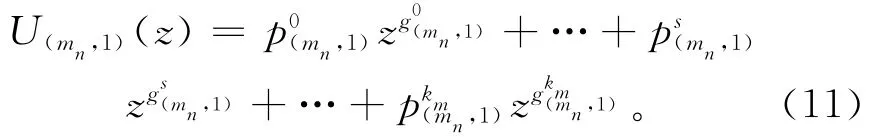
为获得各层子系统的发生函数，引用运算符Ω，由式（8）和式（10），可得第3层子系统hs的发生函数为

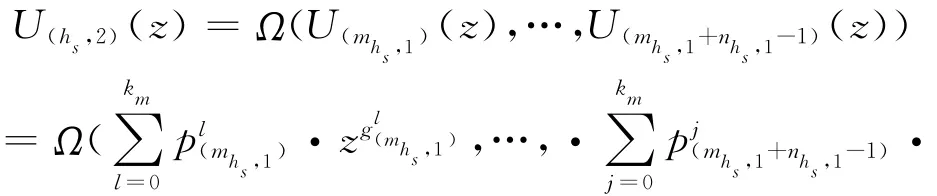
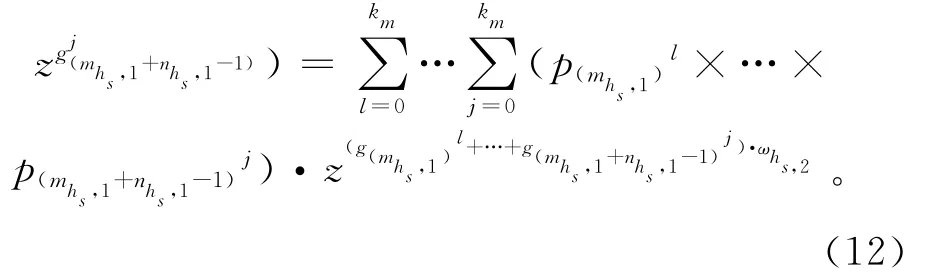
由式（11）和式（12）不难推出，整个系统在L层的发生函数为

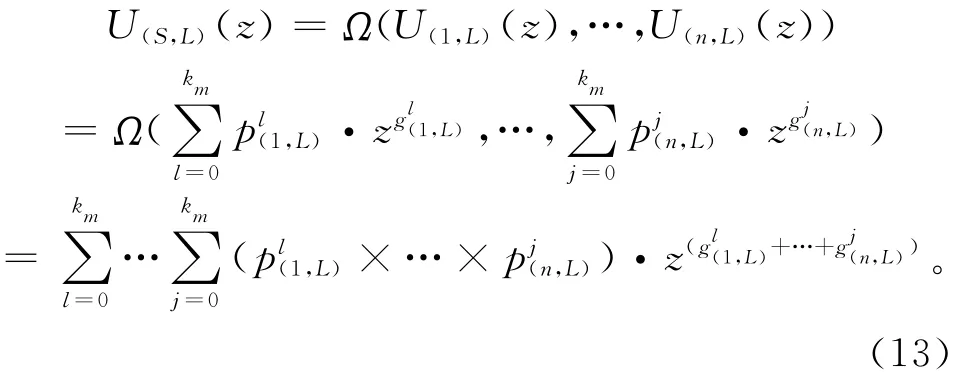
可靠度是可修系统重要的可靠性指标之一，对于制造系统而言，可靠度是指系统性能水平达到任务性能水平的概率。一旦制造系统的发生函数Us（z）确定下来，其可靠度即不难求出。定义：系统的性能水平大于或等于任务需求性能水平时系统可靠，否则系统失效，用公式表示为

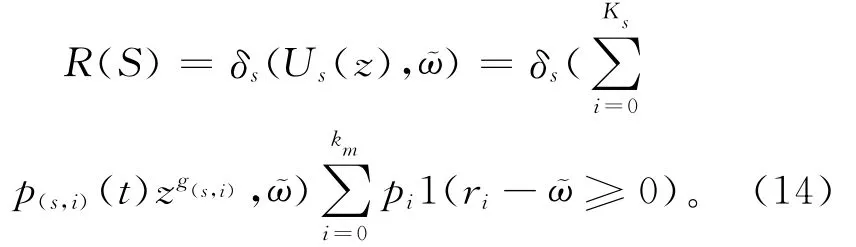
式中：1（⊙）为示性函数，当ri≥时为1，否则为0；δs为算子；Rm为系统性能参数；ri为系统性能取值；pi为系统性能取值为ri时的概率取值。

5 算例分析

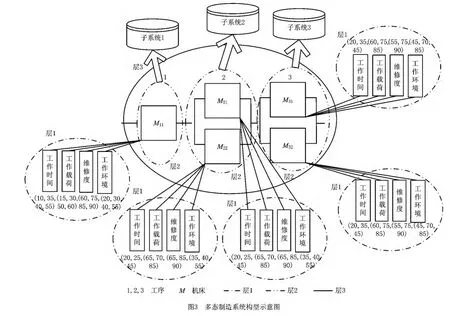
图3所示为多态制造系统构型示意图，用于加工某发动机缸体的主轴承孔，主要由钻、镗、铰三个工序组成，每道工序分别由若干台性能、结构相同的可维修机床并联而成。机床M11看作子系统1，并联机床M21和M22，M31和M32分别看作子系统2和子系统3，每台机床的可靠性认为主要是由工作时间、工作载荷、维修度和工作环境决定的。机床的性能退化主要由刀具磨损引起，实际生产过程中刀具的磨损退化维修情况已知。第一道工序的机床在工作过程中共有4种状态（状态0，状态1，状态2和状态3），其余工序的机床在工作过程中均有3种状态（状态0，状态1和状态2）。各机床的初始状态和性能退化状态转移率等如表2所示，P（Mys，n）（0）为机床Mys的初始状态，ηMys（ji）为机床Mys从高性能状态j到低性能状态i的转移率。系统任务性能水平＝35，求系统的稳态可靠度。

表2 机床性能退化过程状态转移

5．1 各机床多态性分析

由所给条件和第2章衰退过程分析方法，各机床的瞬时状态转移矩阵分别为

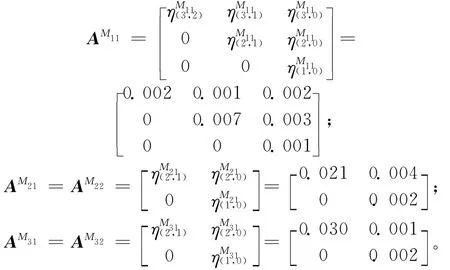
在稳定状态下，根据机床的性能衰退规律，由各机床从高性能状态向低性能状态的转移率求出各机床的稳态概率。

由式（4）～式（6）和初始条件，可得：

（1）机床 M11

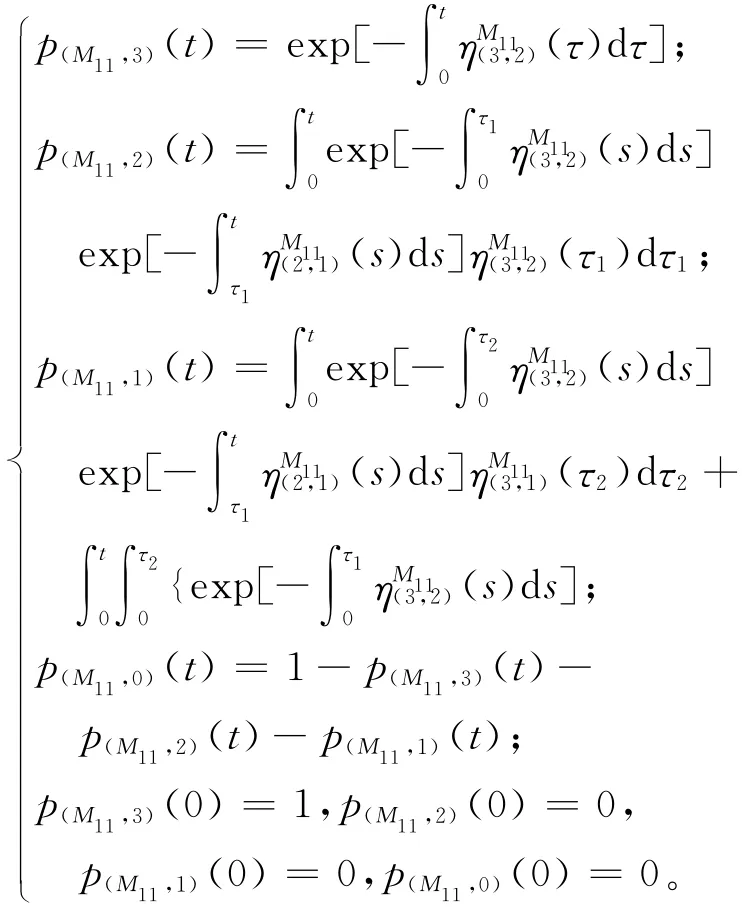
各状态的稳态概率

p（M，3）＝0．405，p（M，2）＝0．412，

1111

p（M11，1）＝0．283，p（M11，0）＝0．096。

（2）机床 M21和M22

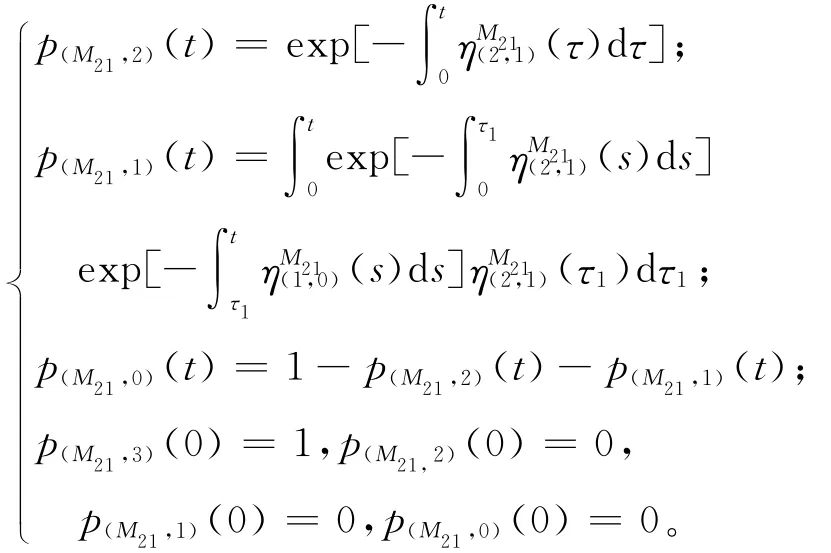
各状态的稳态概率：

p（M21，2）＝p（M22，2）＝0．523，

p（M21，1）＝p（M22，1）＝0．379，

p＝p＝0．167。

（M21，0）（M22，0）

（3）机床 M31和M32

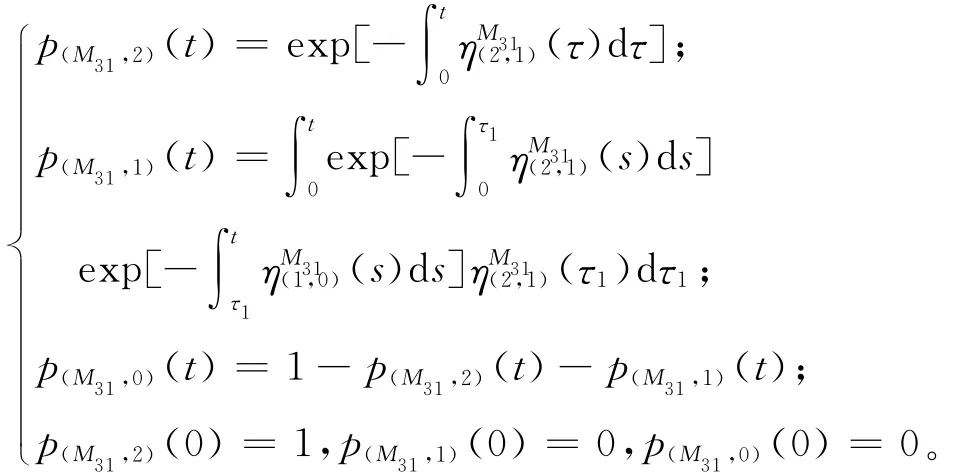
各状态的稳态概率：

p（M31，2）＝p（M32，2）＝0．309，

p（M31，1） ＝p（M32，1） ＝0．322，

p（M31，0）＝p（M32，0）＝0．063。

5．2 系统可靠性分析

并联

算再例与中机，床系M统由串机联床而M成21。和对M该22系并统联进、M行31可和靠M性3211分析，按照第4章的方法，对系统进）：行层级划分。该系统可以分为3个层级（如图3最上一层（第3层）为相互串联的子系统1、子系统2和子系统3，第（二第层一为层每）个为子性系能衰统退所过包程含中的影各响台机机床床可，最靠下性边的一各个层因素，主要为机床的工作时间、工作载荷、维修度和工作环境。图2给出了机床各影响因素在不同状态下的性能取值。其中：（10，15，60，20），（35，30，75，30），（40，50，85，40）和（55，60，90，55）分别表示机床M11的工作时间、工作载荷、维修度和工作环境在状态0、状态1、状态2和状态3下的性能取值。此处，各并联机床的性能机构相同。不难推出，并联机床相对于本层级其他机床的权重为0．5，即机床M21相对于M22的权重为0．5，机床M31相对于M32的权重也为0．5。分析影响机床性能的各因素，运用层次分析法中评价矩阵的建立方法，聘请机械设计、制造、维修和使用四个领域的四位专家对影响因素Py（y＝1，2，3，4）进行两两评价，根据第4章模糊评价矩阵构建方法和图3的指标层次结构，共可形成12个模糊关系矩阵，对其进行归一化处理并进行模糊变换，可构造出模糊评价矩阵，同时各指标权重的计算结果如表3所示。

表3 模糊评价矩阵和各指标相对权重

由第3章的式（8），对机床M11下属的第一层各因素求发生函数，可得：

U1M，111（z）＝0．405×z55＋0．412×z40＋0．283×z35＋0．096×z10；

U2M，111（z）＝0．405×z60＋0．412×z50＋0．283×z30＋0．096×z15；

U3M，111（z）＝0．405×z90＋0．412×z85＋0．283×z75＋0．096×z60；

U4M，111（z）＝0．405×z55＋0．412×z40＋0．283×z30＋0．096×z20。

当考虑系统不能修复如新时，由式（11）～式（13）可得系统的发生函数为

Us（z）＝Ω（U1，2（z），U2，2（z），U3，2（z））＝Ω（0．016×z88＋0．167×z81＋…＋0．009×z23，0．274×z74＋0．198×z66＋…＋0．028×z57，0．095×z68＋0．099×z62＋0．004×z34）＝0．000 4×z162＋0．002×z89…＋0．000 036×z57。

由式（14）可得系统可靠度 R（S）＝δs（Us（z），35）＝0．000 4＋0．002＋…＋0．046＝0．73。

假设系统在维修后能恢复至全新状态，则系统的发生函数为

Us（z）′＝Ω（0．103×z88＋0．142×z81＋…＋0．026×z23，…，0．302×z68＋0．002×z34）＝0．002 4×z162＋0．065×z89…＋0．031×z57。

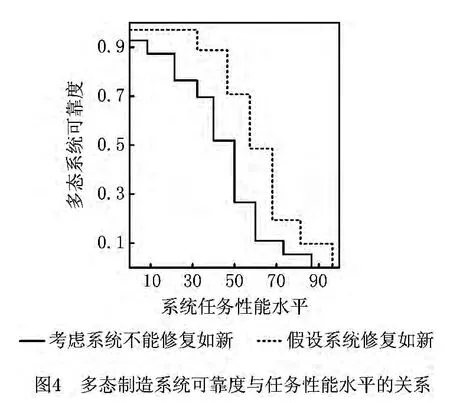
由式（14）可得到上述两种情况下的多态制造系统可靠度与任务性能水平的关系，如图4所示。

由图4可以看出，当考虑系统不能修复如新时，其在相同任务性能水平下的可靠度低于假设能修复如新时系统的可靠度，这是因为后者是假设系统在发生故障后，在指定的更换时刻被一个完全相同的系统所取代，所以结果与实际情况相符。

当考虑性能衰退规律、用传统的方法直接建模求解时，系统的状态数为34×4＝324，运用UGF法可将系统的状态数缩减为15种状态。采用模糊层次分析法，决策者无论对单一因素重要性的把握，还是在因素较多的复杂情况下，都能充分利用决策者的偏好信息构造模糊一致矩阵，避免一般层次分析法中判断矩阵不满足一致性带来的问题，从而保证评价结果的公正性和可靠性分析的正确性。

6 结束语

本文建立了单机床系统性能衰退过程的Markov模型，分析了机床的各种状态。结合非时齐Markov理论，探讨了机床从高性能状态向低性能状态转移的概率组合，进而求出性能转化的状态转移率。结合UGF法和模糊层次分析法，对非串行制造系统进行层级划分，得出单机床与子系统、子系统与总系统之间的性能映射关系，根据系统的发生函数求出系统的可靠度。通过具体实例，由机床各状态的稳态概率推算出多态制造系统的可靠度与任务性能水平的关系，算例的计算结果验证了应用Markov进行多态制造系统可靠性建模的有效性和分析方法的先进性。

［1］ ZHANG Guozhi，YANG Guang，GONG Yinghai．Reliability analysis of complex systems［D］．Harbin：Harbin Institute of Technology，2009（in Chinese）．［张国志，杨 光，巩英海．复杂系统可靠性分析［M］．哈尔滨：哈尔滨工业大学，2009．］

［2］ LISNIANSKI A，LEVITIN G．Multi－state system reliability：assessment，optimization and applications［M］．Singapore City，Singapore：World Scientific，2003．

［3］ LEVITIN G．The universal generating function in reliability analysis and optimization［M］．Berlin，Germany：Springer－Verlag，2005．

［4］ WU Jun，SHAO Xinyu，DENG Chao，et al．Reliability prediction system development based on performance degradation［J］．Computer Integrated Manufacturing Systems，2011，17（1）：191－197（in Chinese）．［吴 军，邵新宇，邓 超，等．基于性能劣化的可靠性预测与系统开发［J］．计算机集成制造系统，2011，17（1）：191－197．］

［5］ WANG Lingzhi，XU Yugong，ZHANG Jiadong．Optimization of reliability－centered preventive maintenance for multi－component systems［J］．Computer Integrated Manufacturing Systems，2008，14（10）：2042－2046（in Chinese）．［王灵芝，徐宇工，张家栋．以可靠性为中心的多部件系统预防性维修优化研究［J］．计算机集成制造系统，2008，14（10）：2042－2046．］

［6］ ZHOU Jinyu，XIE Liyang．Common cause failure mechanism and risk probability quantitative estimation of multi－state systems［J］．Chinese Journal of Mechanical Engineering，2008，44（10）：77－82（in Chinese）．［周金宇，谢里阳．多状态系统共因失效机理与定量分析［J］．机械工程学报，2008，44（10）：77－82．］

［7］ LIU Yu．Multi－state complex system reliability modeling and maintenance decision［D］．Chengdu：University of Electronic Science and Technology of China，2010（in Chinese）．［刘 宇．多状态复杂系统可靠性建模及维修决策［D］．成都：电子科技

大学，2010．］

［8］ ZHANG Junyi，XIE Liyang，LI Bing，et al．Reliability analysis of non－series manufacturing systems based on Petri nets［J］．Journal of Mechanical Engineering，2009，45（12）：95－101（in Chinese）．［张君一，谢里阳，李 兵，等．基于Petri网的非串行制造系统的可靠性分析［J］．机械工程学报，2009，45（12）：95－101．］

［9］ FENG Hutian，YIN Aihua，HAN Jun．Reliability eigenvalue and evaluating index of strongly coherent multistate system［J］．Journal of Nanjing University of Science and Technology，2003，27（2）：137－140（in Chinese）．［冯虎田，尹爱华，韩 军．强理智多态系统可靠性特征量及评价指标［J］．南京理工大学学报：自然科学版，2003，27（2）：137－140．］

［10］ LEVITIN G，XING Liudong．Reliability and performance of multi－state systems with propagated failures having selective effect［J］．Reliability Engineering and System Safety，2010，95（6）：655－661．

［11］ AMARI S V，XING Liudong，SHRESTHA Akhilesh，et al．Performability analysis of multistate computing systems using multivalued decision diagrams［J］．IEEE Transactions on Computers，2010，59（10）：1419－1433．

［12］ SHARMA S P，KUMAR D，KUMAR A．Reliability analy

sis of complex multi－robotic system using GA and fuzzy meth

odology［J］．Applied Soft Computing，2012，（12）：405－415．［13］ LI Chunyang，CHEN Xun，YI Xiaoshan，et al．Reliability analysis of multi－state system with multiple performance parameters based on vector－universal generating function［J］．Acta Armamentarll，2010，31（12）：1604－1610（in Chinese）．［李春洋，陈 循，易晓山，等．基于向量通用生成函数的多性能参数多态系统可靠性分析［J］．兵工学报，2010，31（12）：1604－1610．］

［14］ LIU Y，KAPUR K C．Customer's cumulative experience measures for reliability of non－repairable aging multi－state systems［J］．Quality，Technology and Quantitative Management，2007，4（2）：225－234．

［15］ ZHANG Genbao，LIU Jian，WANG Guoqiang．Fuzzy reliability allocation of CNC machine tools based on task［J］．Computer Integrated Manufacturing Systems，2012，18（4）：768－774（in Chinese）．［张根保，柳 剑，王国强．基于任务的数控机床模糊可靠性分配方法［J］．计算机集成制造系统，2012，18（4）：768－774．］