基于报贩模式的供应链收益分享策略

李 劲，吴政治，王 华

（1．昆明理工大学 质量发展研究院，云南 昆明 650093；2．昆明理工大学 研究生院，云南 昆明 650093）

0 引言

随着全球化的高度竞争与市场的复杂多变，企业为了及时满足客户需求，必须不断进行技术创新。因此，许多高科技电子产品的生命周期均快速缩短，例如全球一年导入的手机模型有上千种，但平均寿命少于10个月。当一个新型产品导入市场时，旧产品就会萎缩，商家会抓紧时间将剩余产品以便宜价格销售。因此，构建一个适合供应商与零售商双方利益协调的机制非常重要，通过整体供应链的有效运作与管理，使供应链中的成员能密切合作，富有弹性地回应市场需求，降低供应链的库存风险与成本。产品销售通常会含有质量风险，从而造成额外成本。其中尤以电子产品为甚，许多质量不良产品送至客户后均会退回换新。因此，质量管理的好坏是供应链成本支出的重点之一，若消费者买到失效产品，则商家不仅要给消费者补足良好的产品，还要额外增加运费成本，而破坏信誉所造成的损失更难以估计，这些都可称为质量风险成本。抽样检验是降低质量风险成本的重要方法，一个有效率的抽样检验，可提升供应链产品的信誉并降低成本。我国是电子产品制造业大国，国内相关产业公司数量庞大、竞争激烈、产品生命周期短，具有明显的季节性商品特征，而且质量良莠不齐、市场风险大，如何制定出一套有效的收益分享策略来应对这些问题，使供应链成员达到双赢，对于企业可持续发展而言是一项重要的课题。报贩模型一直以来被大量应用于季节性商品的库存决策分析，在制造业和零售业等方面也有广泛应用。传统的供应链模式通常是由零售商管理库存，近年来的研究发现，供应商管理库存（Vendor Managed Inventory，VMI）比传统模式能获得更大的收益。在VMI模式中，上游供应商可直接了解市场情况，控制库存与订货量，降低牛鞭效应，减少库存成本与缺货成本，加上双方若签订适当的寄售合约（consignment contract），则更能使下游零售商推销产品、刺激销售量，使双方均能获得更多收益。

本文主要研究两级供应链并同时考虑市场风险与质量风险，以报贩问题为范围来比较传统供应链与VMI模式的利益差异；同时在VMI部分，探讨如何使供应链成员收益最大化以及如何分享收益。已有文献中，探讨VMI与供应链收益分享的相关文献很多，许多学者考虑不同因素提出了策略、模式与解决方法。如RU［1］等比较了两种不同的供应链系统，由零售商选择供应链的库存水平和零售价，称为RMCI（retailer managed consignment inventory）模式，由供应商决定库存以及零售商的寄售价，称为VMCI（vendor managed consignment inventory）模式，作者应用博弈论得出VMCI优于RMCI的结论。LEE等［2］讨论了谁该控制库存的问题并比较了两种模式：①寄售合约，由供应商决定库存水平；②传统模式，协调出批发价，由下游零售商决定订货量并承担库存。唐宏祥［3］分析了协调机制对VMI性能的影响。钟磊钢等［4］提出了价格折扣的协调机制。在收益 分 享 方 面，TSAY 等［5］、李 江 峰 等［6］和CACHON［7］对于报贩问题的成员契约问题进行了文献回顾，包括选择批发价、回扣策略、市场价、多级水 平 买 回 或 退 货 策 略 等。WANG 等［8］、GERCHAK等［9］和曹武军等［10］分别设计了收益共享契约，以协调VMI中供应商与零售商的收益。LINH等［11］研究了两期报贩问题的收益分享策略，探讨如何决定销售收入的比例反馈与批发价，以达到成员间的最佳双赢。ZHOU等［12］针对产品价格敏感的市场，提出一个供应链收益分享契约模型来决定产品价格，目标为使总收益最大，结果表明该分享契约模型的收益比传统的好，同时探讨了收益分享的比例在哪一个范围内会使整个供应链成员的收益均增加。QIN等［13］对报贩问题的相关研究进行了回顾，同时提出一些未来研究方向。PAN等［14］探讨了两个制造商与单一零售商间的销售分享与批发价机制，每个制造商能选择批发价契约或销售收入比例反馈契约，还讨论了一个制造商与两个零售商、每个零售商均可选择批发价契约或销售收入比例反馈契约的情况；蔡建湖等［15］从供应链契约的角度研究供应链的协调，对收益分享契约进行了讨论，但其主要假设需求服从正态分布；杨道箭［16］在1个生产商、1个销售商和具有策略行为与风险偏好的客户群体所组成的报贩供应链系统中，从多个方面就其供应链协调问题进行了深入研究。

通过文献综述发现，VMI协调的相关研究取得了一定的成果。然而在其研究中，还很少有同时将市场风险与质量风险因素纳入考虑范围。但是，在现实中面对市场不确定性风险和产品质量风险，将使供应链收益分享的决策复杂化，进而增加供应链系统的成本。为此，本文针对高科技市场生命周期短的电子产品，纳入质量风险因素，提出不同的供应链模式，并应用模型构建分析方法推导出供应链模型，再基于贝叶斯方法建立计量及计数型检验模型，并以决策树推导出相应的数学模型，以达到供应链成本最小化和成员收益最大化，保证企业可持续地健康发展。

1 供应链模式构建

本文研究两级供应链成员收益分享问题，成员含单一上游供应商与下游零售商，供应链成本有制造成本、市场风险成本和质量风险成本。建立两个供应链模式，分别为模式1和模式2，模式中均假设市场需求服从威布尔分布，两模式的质量风险成本均由供应商负责，并应用贝叶斯方法结合质量与成本建立挑选型检验模型，重点放在单一元件规格的检验上。图1为本文的研究框架。

在交货给零售商之前，供应商先以挑选型抽样检验模型来检验产品质量，若有不合格品送到客户手中，则将产生失效成本，产品检验成本与失效成本均由供应商承担。本文建立两个供应链模式，分述如下：

（1）模式1

由下游零售商决定市场价和订货量，并承担市场风险，产品的剩余价值属于零售商。在双方均了解市场风险的情况下，供应商将产品卖给零售商的单价称为批发价，批发价由双方协议而定，然后先以零售商的收益最大化为目标决定最优订货量；供应商则根据零售商的订货量安排生产并交足产品数量，同时承担质量风险成本。因此，模式1是供应商提出批发价，零售商则根据产品订货量的多寡来与供应商讲价。

（2）模式2

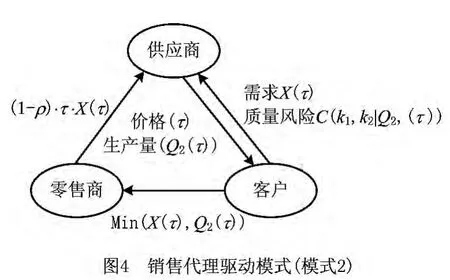
由上游供应商决定市场价和生产量，同时承担市场风险与质量风险成本。目标为求出供应链的总收益最大化与供应商的产品最优制造量；零售商仅扮演销售的角色，收益来自于总收益的提成比例（ρ）。综合市场风险、质量风险成本与最优总收益，双方协议出供应商给零售商的提成比例。

1．1 模型假设

图2为报贩供应链架构图，在不同市场价（τ）下，客户产生不同的需求X（τ）。

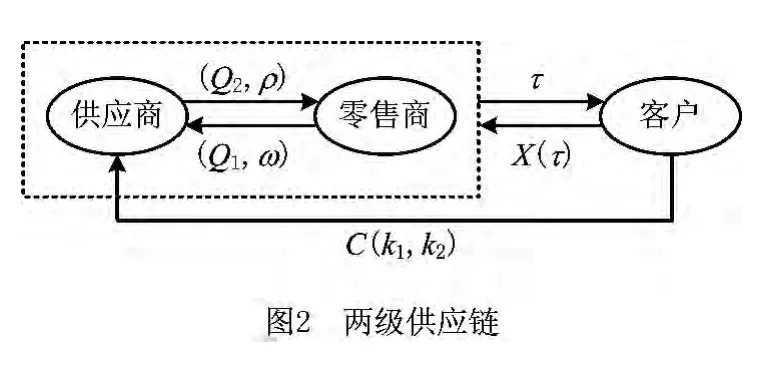
在两种供应链模式中，供应链成员有不同的定购策略和收益分享策略，上游供应商需承担质量风险（C（k1，k2））。模式相关假设如下：

（1）仅考虑单一产品、单期规划。

（2）市场需求分布为X（τ）＝μ（τ）·W。其中：W 为随机变量，μ（τ）受市场价τ的影响，μ（τ）＝a·τ－b，a＞0，b＞0，且b＞1。假设随机变量W 服从威布尔分布，比例参数为λ、形状参数为k。因为

所以X（τ）～Weibull（μ（τ）·λ，k），不同价格下的市场需求量会影响λ。

（3）批发价（ω）与提成比例（ρ）的假设。在模式1中，上游将产品卖给下游的价格称为批发价（ω），在双方均了解市场风险的情况下协议出批发价。在模式2中，提成比例（ρ）将决定双方的收益，但因为上游还需承担质量风险成本，所以双方也将该成本纳入协议，来决定双赢的提成比例。

（4）质量风险成本（C（k1，k2））的假设。假设模式1及模式2的质量风险成本均由供应商承担，并且利用检验模型来减少质量风险成本，检验模型中的单位产品检验成本为k1，单位产品失效成本为k2。

1．2 模型参数

模型所需参数定义如下：（1）决策变量

τ为市场价；

Q1（τ）为模式1中价格τ时的产品订货量；

Q2（τ）为模式2中价格τ时的产品生产量；

ω为上游供应商的单位产品批发价；

ρ为单位产品的提成比例，即市场总收入的提成比例。

（2）其他参数

X（τ）为价格τ下的产品需求量，X（τ）＝μ（τ）·W；

c为上游供应商的单位产品制造成本；

B为单位产品的缺货成本；

g为单位产品的剩余价值；

UP为上游供应商的收益；

DP为下游零售商的收益；

TP为供应链成员的总收益。

1．3 模式1

如图3所示的模式1中，下游零售商的收益为销售收入扣除购买成本和市场风险成本。

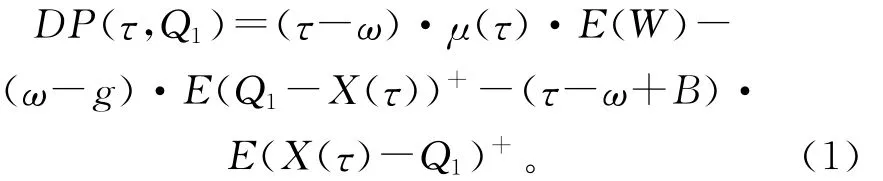
式中：E（Q1－X（τ））＋＝

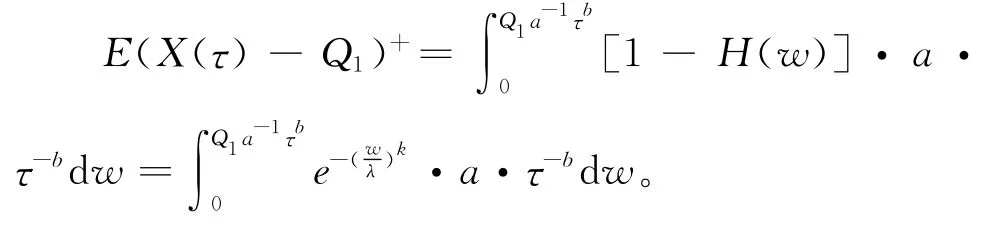
式中H（w）为随机变量W 的累积概率密度函数。

对零售商期望收益（式（1）），固定价格τ针对Q1微分，可得价格τ下的最优产品订货量

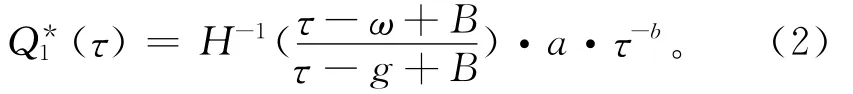
式中H－1（·）为随机变量W 的累积概率密度函数的反函数。

将式（2）代入式（1），再对τ微分，可得最优市场价τ＊。但τ＊的具体方程不易求解，需以数值分析方法求得近似值。为符合实际情况与简化计算，本文设τ为整数值，求出每个τ值的订货量，再代入式（1）求出零售商的最大收益值，就可决定τ＊和Q＊1（τ＊）。

上游供应商的期望收益为产品卖给零售商的批发价减去制造成本乘以订货量，但真实收入需再扣除质量风险成本，期望公式为

E（UP（τ＊））＝（ω－c）·Q＊1（τ＊）－E［C（k1，k2）］。

1．4 模式2

在如图4所示的模式2中，只考虑市场风险时供应链的总收益如下：

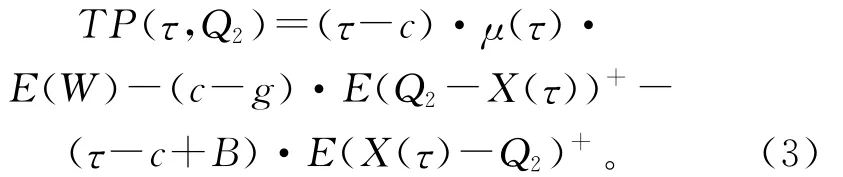
式中E（Q2－X（τ））＋与E（X（τ）－Q2）＋期望值的计算与模式1相同。针对式（3），固定τ对Q2微分，可得价格τ下的最优产品生产量

将式（4）代入式（3）后，针对τ微分，可得最优价格τ＊。为符合实际情况与简化计算，本文设τ为整数值，求出每个τ值的订货量，再找出整体供应链的总收益最大值，就可决定τ＊和Q＊2（τ＊）。双方决定提成比例后，可得到零售商的期望总收益值

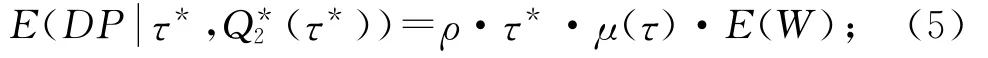
供应商的期望总收益值

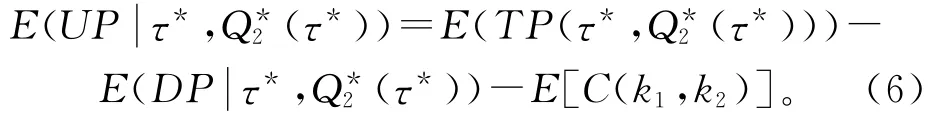
2 检验模型构建

2．1 模型参数

N为产品需求量；

n为抽验样本数；

Xi为批量中第i个产品的功能表现值；

P（v）为参数V＝v时合格产品的概率；

S为样本功能表现值的总和s为其一样本值；

y为抽验样本中不合格品的个数；

k1为单位产品的检验成本；

k2为单位产品的失效成本；

a1为第二阶段决策为“停检”；

a2为第二阶段决策为“全检”；

R（y）为y个不合格品中所需额外检验产品的个数；

YN－n为N－n个剩余未检验产品中的不合格品个数；

R（YN－n）为YN－n个不合格品中所需额外检验产品的个数。

2．2 模型假设

假设模式1中需交给零售商的产品总数为Q1，模式2的最终生产总数为Q2，在检验模型中称该数量为产品需求量（N）。采用挑选型检验，给定样本数n，若检验时有不合格品，则选取新产品持续检验，直至得到n个合格品为止，在该过程中，均会产生单位检验成本k1，检验出不合格品时还会产生额外检验成本，直至确认新的合格品为止。在N－n个剩余产品中，若有不合格品送至客户手中，则每件不合格品将产生失效成本（k2），包括信誉、运输成本的损失。

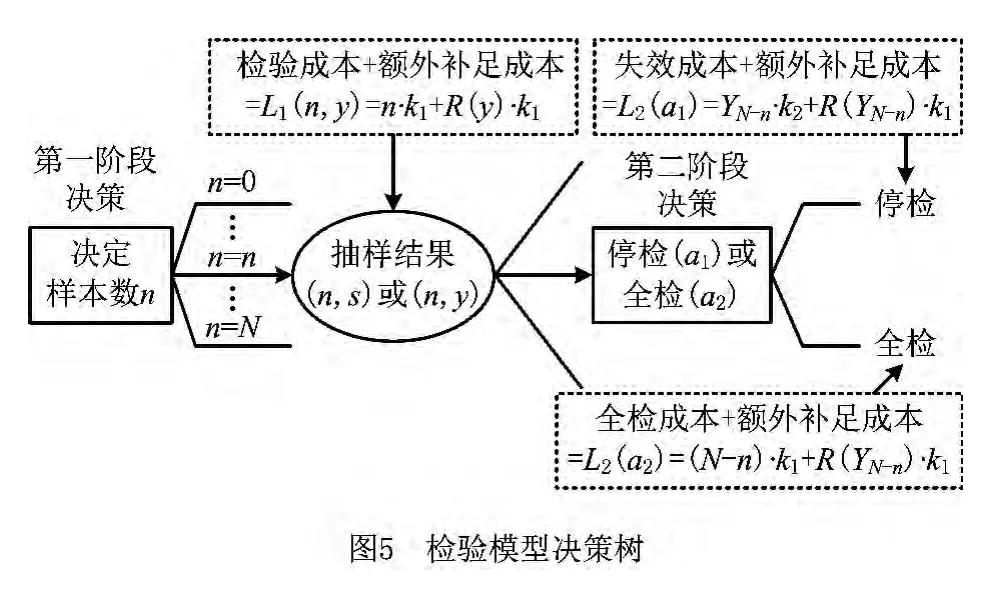
以动态规划推导检验模型的目标成本，由后向前推可得到整体决策模式及目标函数。该检验模型包括两阶段：第一阶段为决定最优抽验数，第二阶段为决定“停检”或“全检”。当停检时，剩余N－n个产品中就可能有不合格品送至客户手中；当全检时，就无此顾虑，但需较多检验成本。如何平衡这些风险以使质量风险的总成本最小，是该检验模型的目标。采用贝叶斯方法，可以先估算相关成本，利用决策树（如图5）寻找最优决策。

（1）第一阶段决策因为不合格品数y有不同的可能值，所以期望成本为E［L1（n）］ ＝。最后得到检验模型最小成本目标函数为两阶段期望成本相加的最小值［L（n）］＝min｛E［L1（n）］＋E［L2（n）］｝。求得最小期望成本时的样本数（n），就是检验模型的最优抽样数。

（2）第二阶段决策选择“停检”（a1）时，期望成本为E［L2（a1）］＝E（YN－n）·k2＋E［R（YN－n）］·k1。选择“全检”（a2）时，期望成本为E［L2（a2）］＝（N－n）·k1＋E［R（YN－n）］·k1。

2．3 计量型检验模型

由2．2节的假设，若V的检验前分布为Gamma（α，β），则产品合格率为

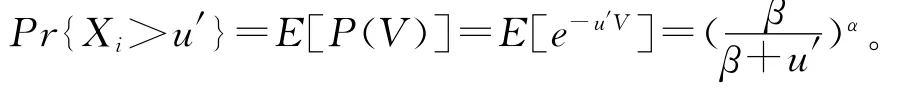
由图5知，第二阶段决策的期望成本如式（7）和式（8）：

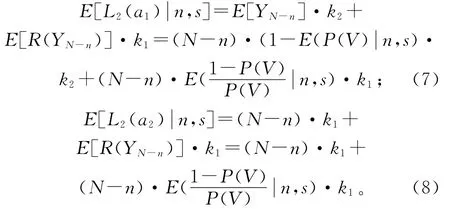
当抽样结果为（n，s）时，第二阶段的期望成本为

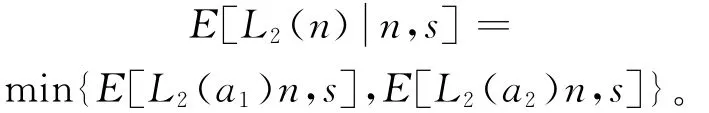
将此成本回推至第一阶段决策，其样本数为n时，可得

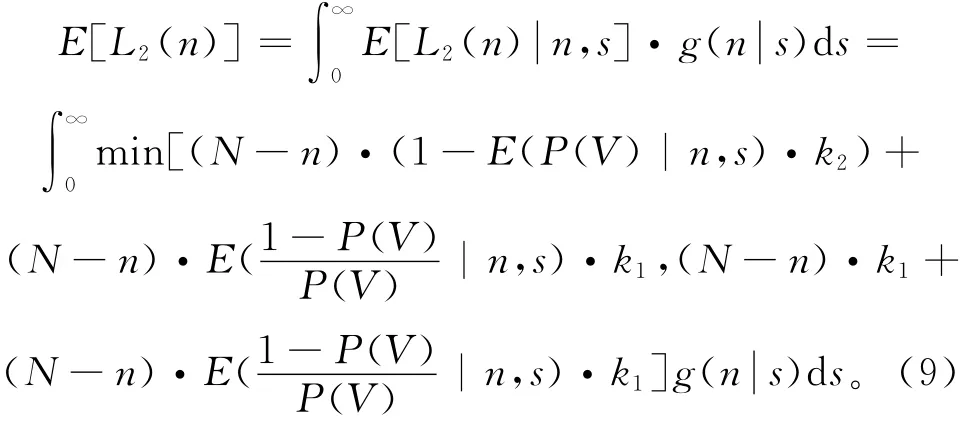
当1－E（P（V）n，s）≤k1/k2时，“停检”优于“全检”；否则是全检优于停检。

第一阶段的期望检验成本为：

计量型检验模型的最小成本目标函数为

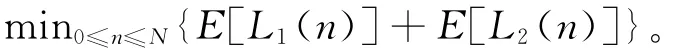
2．4 计数型检验模型

若检验出第k个产品为不合格品，则Yk＝1，否则Yk＝0。产品被检验为合格的概率为

Pr｛Yk＝0｝＝Pr｛Xk＞u′｝＝E（P（V））＝

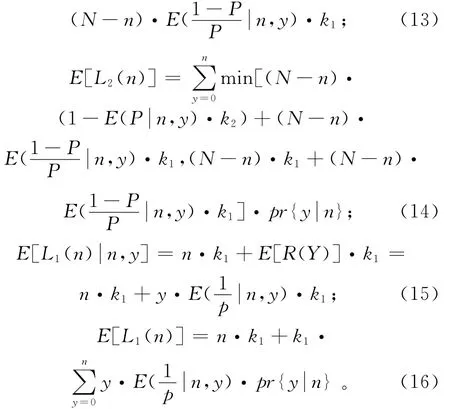
最小期望成本目标函数为

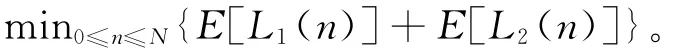
若1－E（P n，0）≥k1/k2，则选择“全检”；若1－E（P n，n）≤k1/k2，则采取“停检”。而在1－E（P n，0）≤k1/k2且1－E（P n，n）＞k1/k2时，计数型检验模型存在一个c＊，0≤c＊≤n，当0≤y≤c＊时采取“停检”；当y＞c＊时采取“全检”。

3 案例验证与分析

为研究本文提出的模式是否适用于电子产品等制造产业，以中国西南地区机电制造业最发达的重庆市调研的数据为基础，案例相关参数设定如下：

随机变量W～Weibull（λ＝3 200，k＝5），影响市场需求的参数a＝2 253．6、b＝2．15，因此市场需求的分布为X（τ）～Weibull（3 200·2 253·6·τ－2．15，5）。供应商的单位产品制造成本c＝10；市场风险方面，单位产品缺货成本B＝15，单位产品剩余价值g＝4。质量风险方面的参数将在3．1节说明。

3．1 检验模型的成本分析

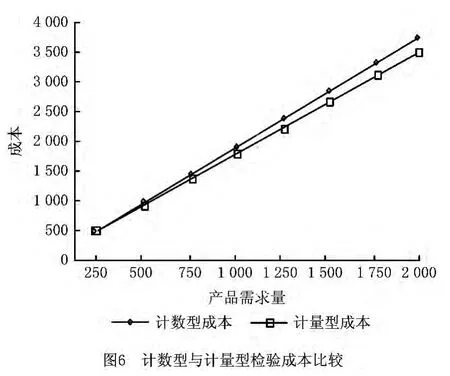
首先，探讨检验模型的成本。检验模型中，单位产品失效成本、产品需求量以及不合格品数均会影响检验模型成本。分析不同的产品需求量（N）对两种检验模型的影响，其他因素固定。图6为实验结果，当产品需求量在［250～2 000］区间内时，计量型检验成本小于计数型检验成本，且产品需求量越大时，两检验模型成本的差异越大。

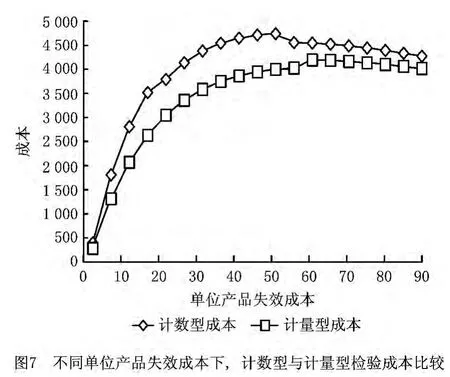
其次，分析不同的单位产品失效成本对于两种检验模型的影响，其他因素固定。图7为实验结果，当单位产品的失效成本在［0，95］区间内时，计量型检验成本小于计数型检验成本。

再次，分析不同的产品不合格品数对于两种检验模型的影响，其他因素固定。图8为实验结果，当产品不合格数为在［0，48］区间内时，计量型检验成本小于计数型检验成本，且产品不合格数越大时，两检验模型的成本差异越大。在下面的数据分析中，上游供应商将只考虑成本较低的计量型检验模型。

图6～图8表明，计量型检验相对于计数型检验的成本要低，这是因为：在信息相同的情况下做决策，计量型检验可以利用的信息比计数型检验要多，计数型检验仅使用（good＝0，bad＝1），因此在贝叶斯决策方法的预先事后分析（preposterior analysis）下，计量型抽样检验比计数型抽样检验所得的期望成本低。

3．2 供应链模式的数据分析

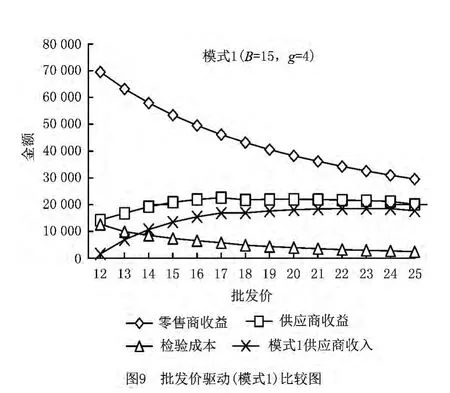
下面以固定的市场价为基础，比较两种模式的优劣。在模式1中，双方将协议批发价；零售商希望以较低的价格买入，当零售商购买成本低时，市场售价较低，市场需求量也会提高。供应商则希望以较高的价格卖给零售商，但批发价高时，零售商就会提高产品的市场售价，相应的需求量会下降，产品订货量也会降低。因此，供应商收益并非随着批发价的提高而增加。模式1中在批发价为12～25时，对供应链成员收益的影响结果如表1和图9所示。

由图9可发现，下游零售商的收益随批发价的增加而减少，供应商在批发价为20时有最优收益（21 970．2），之后收益缓慢下降；批发价越高，零售商的订货量会下降，检验成本也随之降低。供应商收益扣除检验成本的趋势与供应商的收益相似，随着批发价的增大，增加幅度减小，且在批发价为23时有最优收入（18 510．74）。

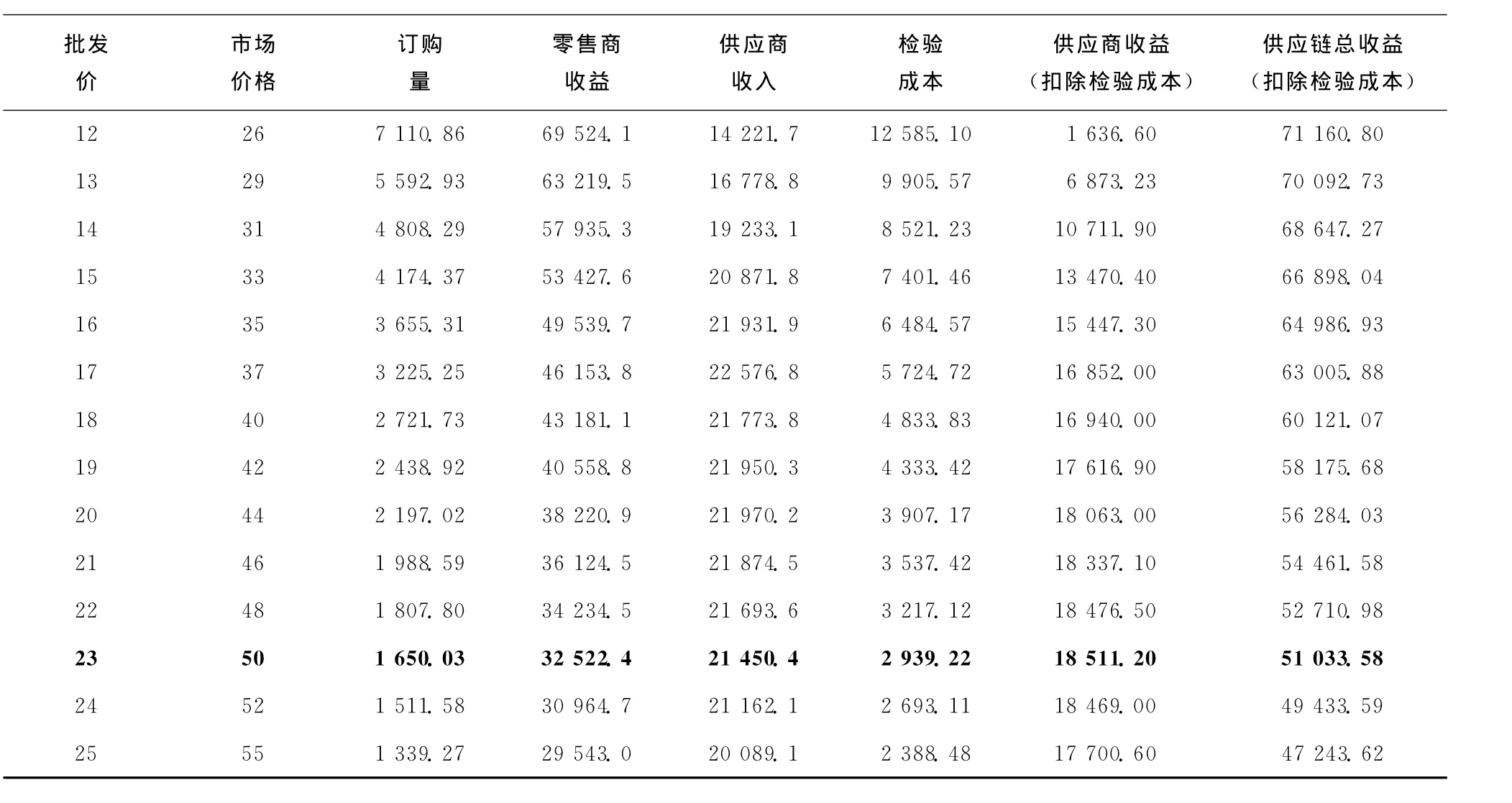
表1 模式1实验结果

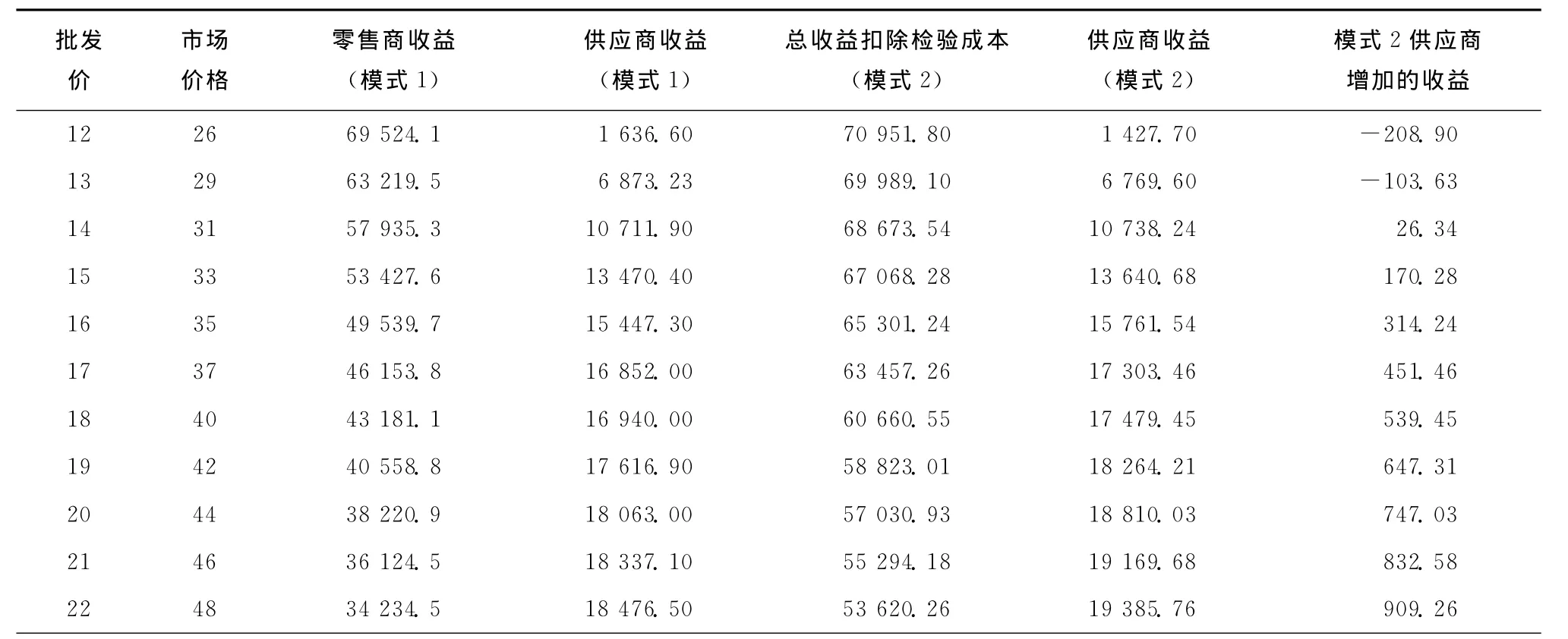
表2 相同市场价下，两模式之间供应链成员收益比较

续表2

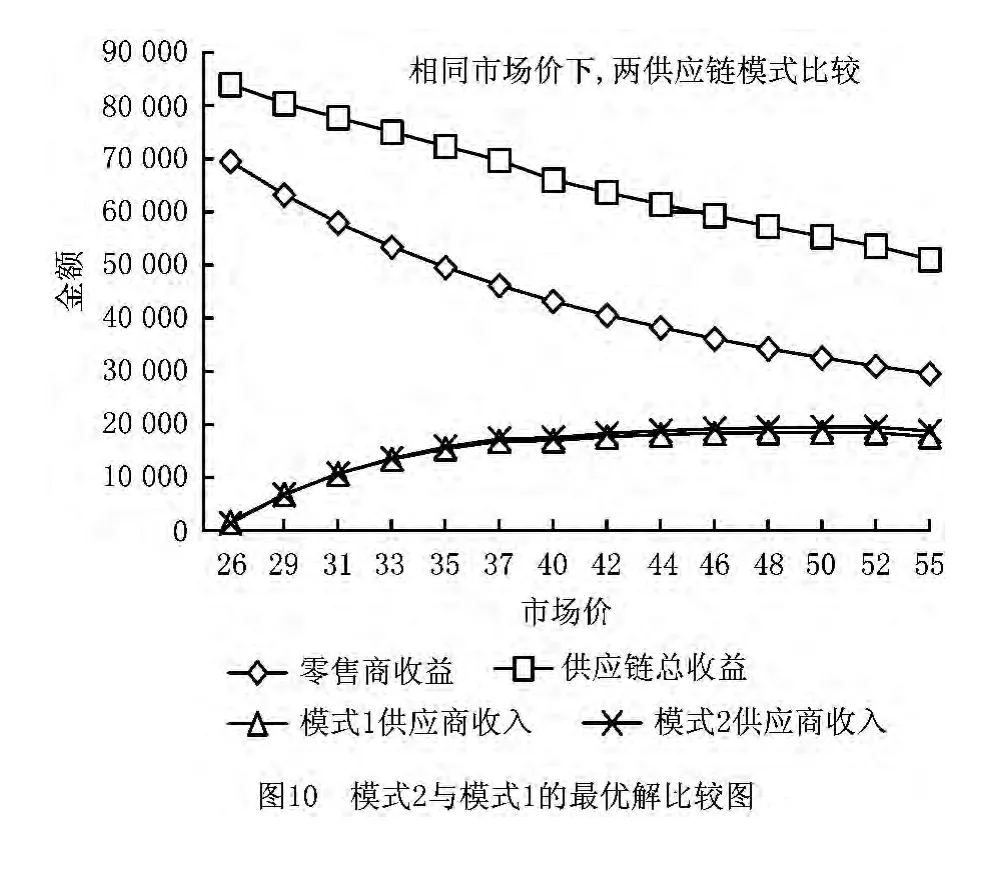
在模式1中，零售商对每个批发价均可找到最优市场价。下面进一步从上游供应商的角度出发，先不考虑模式2的提成比例，在相同的市场价与市场风险下，比较模式1与模式2。市场价为模式1中批发价为12～25时所对应的最优市场价（如图10的横坐标）。实验中：①模式1供应商的收入，是模式1的供应商收益减去检验成本；②模式2供应商的收入，是模式2的供应链总收益扣除检验成本以及相同市场价下的模式1零售商的收益。表2为实验结果，图10为对应的模式2与模式1之最优解的比较。

模式1零售商的收益及模式2供应链的总收益均随市场价的增加而减少，在市场价较小时两者差异也较小，这是因为模式1中零售商的收益太高，如果导致模式2中零售商的收益要与其持平，则供应商需给予相当高的提成比例，这对供应商的收入不利。但随着市场价的提高，模式2供应商的收入大于模式1，且两模式收入的差距逐渐变大，表明市场价高时，上游供应商承担市场的风险优于下游零售商，不仅零售商的收益不会减少（相对于模式1），还可增加供应商的收入，由此可推出提成比例（ρ）的上限与下限。提成比例为零售商抽取总收益的比例，以市场价40为例（如表3）：提成比例下限＝（43 181．1/66 003．5）×100%＝65．4%，表示模式2中零售商的收益与模式1持平；提成比例上限＝（（43 181．1＋539．45）/66 003．5）×100%＝66．2%，表示模式2中的供应商把增加的收益都给予零售商。

表3 固定市场价时，供应链成员的收益变化

4 结束语

本文研究了报贩供应链，同时考虑市场风险与质量风险成本，提出两种供应链模式，建立了挑选型检验模型以降低质量风险，纳入检验成本来探讨供应链成员如何分享收益。得出以下结论：

（1）检验模型方面。对于单一元件检验建立了计量型与计数型两种检验模型，且实验数据分析表明，计量型检验成本较低，故在供应链模式中，供应商应采用计量型检验来降低质量风险成本。

（2）供应链模式方面。本文提出两种供应链模式，模式1由零售商承担市场风险及决定市场价，供应商承担质量风险；模式2则由供应商掌控整体供应链，供应商同时承担市场风险与质量风险，并决定市场价。在相同市场价时，模式1中的零售商会有对应其市场价的订价策略，使零售商收益最大化；若从供应商的角度出发，则模式2中由供应商承担市场风险、决定市场价，供应商从总收益中将相同价格时的最优收益分享给零售商，剩余的收益扣除检验成本为模式2的供应商收入。实验数据分析表明，在市场价较大时，模式2优于模式1，且两模式的差距随市场价的增加而变大。

本文所提供应链模式有三个决策变量（批发价、市场价、订货量），模式2属于集中式机制，其决策空间不须考虑批发价，目标是供应链总收益最大，而模式1属于分散式机制，供应商仅对批发价做决策，目标为寻找批发价以使从零售商所返回的收益最大，而供应链总收益为两个各自收益相加。因此，模式1的供应链总收益可视为零售商的最优（市场价、定货量）限制在某个批发价下，两者收益的总和不会高于模式2的供应链总收益。本文通过数值分析方法得到这个结论，并对两种供应链模式下的最优解进行了比较。下一步的研究可将下游扩展到多个零售商，并且各个零售商的需求量随市场价格波动而变化的情况；产品订购周期方面，可考虑两周期以上的订购时间，并且将可能影响的参数纳入考虑，如产品订购的前置时间等。

［1］ RU J，WANG Y．Consignment contracting：who should control inventory in the supply chain？［J］．European Journal of Operational Research，2010，201（3）：760－769．

［2］ LEE C C，CHU W H J．Who should control inventory in a supply chain［J］．European Journal of Operational Research，2005，164（1）：158－172．

［3］ TANG Hongxiang．Analysis on influence of VMI on the performance of supply chain［J］．Chinese Journal of Management Science，2005，12（2）：60－65（in Chinese）．［唐宏祥．VMI对供应链性能的影响分析［J］．中国管理科学，2005，12（2）：60－65．］

［4］ ZHONG Leigang，HU Yong，ZHANG Cuihua．The coordination strategy analysis of a kind of supply chain on VMI［J］．Chinese Journal of Management Science，2006，14（6）：92－97（in Chinese）．［钟磊钢，胡 勇，张翠华．一类供应商管理库存供应链协调策略研究［J］．中国管理科学，2006，14（6）：92－97．］

［5］ TSAY A A，NAHMIAS S，AGRAWAL N．Chapter 10：modeling supply chain contracts：a review［M］//Quantitative Models for Supply Chain Management．Druten，the Nether－lands：Kluwer Academic Publishers，2003：299－336．

［6］ LI Jiangfeng，ZHANG Shunming，LIU Weifang．Newsvendor model with pricing and ordering decision－making based on pessimistic bias［J］．Systems Engineering，2013，31（1）：105－110（in Chinese）．［李江峰，张顺明，柳维芳．基于悲观偏差的定价订购报贩模型［J］．系统工程，2013，31（1）：105－110．］

［7］ CACHON G P．Supply chain coordination and revenue sharing contract：strength and limitation［J］．Management Science，2005，51（1）：30－44．

［8］ WANG Yunzeng，JIANG Li，SHEN Zuojun．Channel performance under consignment contract with revenue sharing［J］．Management Science，2004，50（1）：34－47．

［9］ GERCHAK Y，KHMELNITSK E．A consignment system where suppliers cannot verify retailer｀s sales reports［J］．International Journal of Production Economics，2003，83（1）：37－43．

［10］ CAO Wujun，LI Chenggang，WANG Xuelin，et al．Analysis on the revenue sharing contract in VMI［J］．Journal of Industrial Engineering and Engineering Management，2007，21（1）：51－55（in Chinese）．［曹武军，李成刚，王学林．VMI环境下收入共享契约分析［J］．管理工程学报，2007，21（1）：51－55．］

［11］ LINH G T，HONG Y．Channel coordination through a revenue sharing contract in a two－period newsboy problem［J］．European Journal of Operational Research，2009，198（3）：822－829．

［12］ ZHOU Y W，YANG S．Pricing coordination in supply chains through revenue sharing contracts［J］．Information and Management Sciences，2008，19（1）：31－51．

［13］ QIN Y，WANG R，VAKHARIA A J，et al．The newsboy problem：review and directions for future research［J］．European Journal of Operational Research，2011，213（2）：361－374．

［14］ PAN K，LAI K K，LEUNG S C H，et al．Revenue－sharing versus wholesale price mechanisms under different channel power structures［J］．European Journal of Operational Research，2010，203（2）：532－538．

［15］ CAI Jianhu，ZHOU Gengui．Influence of revenue sharing contracts on the performance of a two－echelon supply chain［J］．Computer Integrated Manufacturing Systems，2008，14（8）：1636－1645（in Chinese）．［蔡建湖，周根贵．收益分享契约对供应链性能的影响分析［J］．计算机集成制造系统，2008，14（8）：1636－1645．］

［16］ YANG Daojian．Supply chain coordination research based on strategic customer behavior［D］．Tianjin：Tianjin University，2010（in Chinese）．［杨道箭．基于顾客策略行为的供应链协调研究［D］．天津：天津大学，2010．］