一类广义变分不等式组的迭代算法

张丽娟，佟慧

(河北大学 数学与计算机学院，河北 保定 071002)

1 预备知识

变分不等式是由Stampacchia[1]在1964年导出的，在工业生产、金融学、社会学等方面有广泛应用，变分不等式理论成为重要的数学分支，它的理论和方法仍在不断发展和创新，许多数学家和工程技术人员都对此问题进行研究[1-9].近来Noor[3]考虑了多个不同非线性算子的变分不等式组，利用投影算子方法，提出并分析迭代算法，在适当的条件下证明迭代序列的收敛性.本文主要是在Banach空间下讨论多个不同非线性算子的变分不等式组，得到的结果能够运用到Lp,Wm,p(p>1)等更为广泛的空间.

设B是实Banach空间，B*是它的对偶空间，〈.,.〉是B和B*的偶对(泛函的取值)，2B记为B的子集全体.广义对偶映射Jq(x):B→2B*定义为

Jq(x) = {f*∈B*:〈x,f*〉=‖x‖q,‖f*‖=‖x‖q-1},

q>1是常数.J2称为正规对偶映射，对所有的x∈B，Jq=‖x‖q-2J2.当空间B*是严格凸时,Jq(x)是单值的.假设空间B*是严格凸的，则Jq(x)是单值的.记J2=J,若B=H是Hilbert空间，J2=I是H上的恒等映射.

设C是B的非空闭凸子集.映射Q:B→C称为向阳的，如果

Q(Qx+t(x-Qx))=Qx,∀x∈B,∀t≥0,

映射Q:B→C称为保核的,如果对x∈C有x=Qx.若B是光滑的，则B映为C的向阳非扩张保核映射是唯一确定的.

引理1[10]设B是实光滑的Banach空间,C是B的非空闭凸子集.设QC:B→C是保核的,J,Jq是B上的正规对偶映射和广义对偶映射，则以下结论等价：

a)QC是向阳非扩张的.

b)‖QCx-QCy‖2≤〈x-y,J(QCx-QCy)〉,∀x,y∈B.

c)〈x-QCx,Jq(QCx-y)〉≥ 0,∀y∈C,x∈B.

(1)

引理2[11]设B是实q(q>1)一致光滑的Banach空间,则存在常数cq>0,使得

‖x+y‖q≤‖x‖q+q〈y,Jqx〉+cq‖y‖q,∀x,y∈B.

特别的，B是2-一致光滑的Banach空间，则存在常数c2>0,使得

‖x+y‖2≤‖x‖2+2〈y,Jx〉+c2‖y‖2,∀x,y∈B.

设C是B的非空闭凸子集，Ti:C×C→B,fi:C→B,gi:C→C,i=1,2是给定的非线性映射，考虑变分问题：求点(x*,y*)∈C×C,使得

〈π1T1(y*,x*)+g1(x*)-f1(y*),Jq(x-g1(x*))〉≥0,∀x∈C,π1>0;

(2)

〈π2T2(x*,y*)+g2(y*)-f2(x*),Jq(x-g2(y*))〉≥0,∀x∈C,π2>0.

(3)

这个问题称为广义变分不等式组，其中π1和π2是2个参数，它在研究迭代法的收敛性分析时起重要作用.广义变分不等式组包含了一些特殊型的变分不等式和优化问题.

定理1 设B是光滑Banach空间,Ti(i=1,2):C×C→B是2个任意算子，π1和π2是2个任意正数，则(x*,y*)∈C×C是变分不等式组(2),(3)的解当且仅当(x*,y*)满足算子方程

g1(x*)=QC[f1(y*)-π1T1(y*,x*)],π1>0,

(4)

g2(y*)=QC[f2(x*)-π2T2(x*,y*)],π2>0.

(5)

证明：变分不等式(2)可以写成

〈[f1(y*)-π1T1(y*,x*)]-g1(x*),Jq(g1(x*)-x)〉≥0,∀x∈C,π1>0.

由QC的性质(1),上述公式等价于

g1(x*)=QC[f1(y*)-π1T1(y*,x*)],π1>0.

类似地，变分不等式(3)等价于以下公式

g2(y*)=QC[f2(x*)-π2T2(x*,y*)],π2>0.

2 迭代算法和收敛性分析

利用定理1的2个等价公式，构造变分不等式组解的迭代算法.

算法对任意的初值x0,y0∈C,计算序列{xn}和{yn}，使得

(6)

其中QC是B映为C的向阳非扩张保核映射，π1>0和π2>0是常数，{αn}是(0,1]的序列.

下面用隐迭代序列讨论变分不等式组解的逼近问题.首先给出以下定义.

定义1 映射T:C×C→B称为r强增生的，如果存在常数r>0,使得

〈T(x1,y)-T(x2,y),Jq(x1-x2)〉≥r‖x1-x2‖q,∀x1,x2,y∈C.

定义2 映射T:C×C→B称为γ松弛协强制的，如果存在常数γ>0,使得

〈T(x1,y)-T(x2,y),Jq(x1-x2)〉≥-γ‖T(x1，y)-T(x2,y)‖q,∀x1,x2,y∈C.

定义3 映射T:C×C→B称为(γ,r)松弛协强制的，如果存在常数γ>0,r>0,使得

〈T(x1,y)-T(x2,y),Jq(x1-x2)〉≥-γ‖T(x1，y)-T(x2,y)‖q+r‖x1-x2‖q,∀x1,x2,y∈C.

(γ,r)松弛协强制算子类比强增生算子类广.

定义4 映射T:C×C→B称为关于第1变量μ李普希兹连续，如果存在常数μ>0,使得

‖T(x1,y)-T(x2,y)‖≤μ‖x1-x2‖，∀x1,x2,y∈C.

引理3[12]{sn}是满足下列条件的非负序列：

sn+1≤(1-λn)sn+βn,∀n≥0.

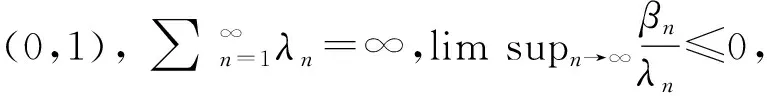
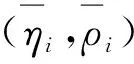
b)0 ≤ω1+π1μ12<1,0≤ω2+π2μ22<1;

c)(θ1+ξ1)(θ2+ξ2)<(1-ω1-π1μ12)(1-ω2-π2μ22),

其中

(9)

则对任意的初值x0,y0∈C，由算法得到的xn，yn分别强收敛到x*和y*.

证明：由式(4)可得

x*=(1-αn)x*+αn{x*-g1(x*)+QC[f1(y*)-π1T1(y*,x*)]},π1>0.

由式(6)和QC的向阳非扩张保核性质可得.

‖xn+1-x*‖=
‖(1-αn)xn+αn{xn-g1(xn)+QC[f1(yn)-π1T1(yn,xn)]}-(1-αn)x*-αn{x*-g1(x*)+
QC[f1(y*)-π1T1(y*,x*)]}‖ ≤
(1-αn)‖xn-x*‖+αn‖xn-x*-[g1(xn)-g1(x*)]‖+
αn‖f1(yn)-π1T1(yn,xn)-[f1(y*)-π1T1(y*,x*)]‖≤
(1-αn)‖xn-x*‖+αn‖xn-x*-[g1(xn)-g1(x*)]‖+
αn‖yn-y*-[f1(yn)-f1(y*)]‖+αn‖yn-y*-π1[T1(yn,xn)-T1(y*,x*)]‖,

其中

‖yn-y*-π1[T1(yn,xn)-T1(y*,x*)]‖≤

‖yn-y*-π1[T1(yn,xn)-T1(y*,xn)]‖+π1‖T1(y*,xn)-T1(y*,x*)‖.

T1关于第2变量μ12李普希兹连续性，得‖T1(y*,xn)-T1(y*,x*)‖≤μ12‖xn-x*‖.由引理2，T1的(γ1,δ1)松弛协强制性且关于第1变量μ11李普希兹连续性，得

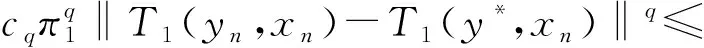
因此

‖yn-y*-π1[T1(yn,xn)-T1(y*,xn)]‖≤θ1‖yn-y*‖,其中θ1由式(7)定义.类似地，利用f1的(η1,ρ1)松弛协强制性且λ1李普希兹连续性，得到

‖yn-y*-[f1(yn)-f1(y*)]‖≤ξ1‖yn-y*‖.

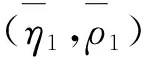
‖xn-x*-[g1(xn)-g1(x*)]‖≤ω1‖xn-x*‖.

其中ξ1和ω1由式(8)和式(9)定义.综上可得

‖xn+1-x*‖≤[1-αn(1-ω1-π1μ12)]‖xn-x*‖+αn(θ1+ξ1)‖yn-y*‖.

(10)

由式(5)、式(6)和QC的向阳非扩张保核性质可得，

‖g2(yn+1) -g2(y*)‖=
‖QC[f2(xn+1)-π2T2(xn+1,yn+1)]-QC[f2(x*)-π2T2(x*，y*)]‖≤
‖f2(xn+1)-π2T2(xn+1,yn+1)-[f2(x*)-π2T2(x*,y*)]‖≤
‖xn+1-x*-[f2(xn+1)-f2(x*)]‖+‖xn+1-x*-π2[T2(xn+1,yn+1)-T2(x*,y*)]‖,

其中

‖xn+1-x*-π2[T2(xn+1,yn+1)-T2(x*,y*)]‖≤
‖xn+1-x*-π2[T2(xn+1,yn+1)-T2(x*,yn+1)]‖+π2‖T2(x*,yn+1)-T2(x*,y*)‖.

T2关于第2变量μ22李普希兹连续性，得‖T2(x*,yn+1)-T2(x*,y*)‖≤μ22‖yn+1-y*‖.由引理2，T2的(γ2,δ2)松弛协强制性且关于第1变量μ21李普希兹连续性，得

从而‖xn+1-x*-π2[T2(xn+1,yn+1)-T2(x*,yn+1)]‖≤θ2‖xn+1-x*‖,其中θ2由式(7)定义.类似地，利用f2的(η2,ρ2)松弛协强制性且λ2李普希兹连续性，得到

‖xn+1-x*-[f2(xn+1)-f2(x*)‖≤ξ2‖xn+1-x*‖.

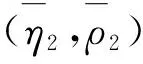
‖yn+1-y*-[g2(yn+1)-g2(y*)]‖≤ω2‖yn+1-y*‖.

其中ξ2和ω2由式(8)和式(9)定义.综上可得

‖yn+1-y*‖≤
‖yn+1-y*-[g2(yn+1)-g2(y*)]‖+‖g2(yn+1)-g2(y*)‖≤
ω2‖yn+1-y*‖+ξ2‖xn+1-x*‖+θ2‖xn+1-x*‖+π2μ22‖yn+1-y*‖.

因此

(11)

把式(11)代入式(10)得出

根据条件(a),(c)由引理3得出

由式(11)可得

参 考 文 献:

[1] STAMPACCHIA G.Formes bilineaires coercivities sur les ensembles convexes [J].C R Acad Sci Paris,1964,258:4413-4416.

[2] NOOR M A,NOOR K I.Resolvent methods for solving system of general variational inclusions[J].J Optim Theory Appl,2011,148:422-430.

[3] NOOR M A,NOOR K I.Projection algorithms for solving a system of general variational inequalities[J].Nonlinear Anal, 2009,70:2700-2706.

[4] IIDUKA H, TAKASHIHA W, TOYODA M. Approximation of solutions of variational inequalities for monotone mappings[J].Panam Math J, 2004,14(2):49-61.

[5] QIN Xiaolong, CHO S Y, KANG S M. Convergence of an iterative algorithm for system of variational inequalities and nonexpansive mappings with applications[J].J Comput Appl Math,2009, 233: 231-240.

[6] YAO Yonghong, NOOR M A, NOOR K I,et al. Modified extragradient methods for a system of variational inequalities in Banach spaces[J]. Acta Appl Math, 2010,110:1211-1224.

[7] VERMA R U. Generalized system for relaxed cocoercive variational inequalities and projection methods[J].J Optim Theory Appl, 2004,121:203-210.

[8] VERMA R U. General convergence analysis for two-step projection methods and applications to variational problems[J].Appl Math Lett, 2005,18:1286-1292.

[9] 徐永春，何欣枫，何震.一类广义变分不等式组的隐迭代算法[J].数学学报：中文版，2010,53(4):751-758.

XU Yongchun, HE Xinfeng, HE Zhen. Implicit iteration algorithms of a class for general variational inequalities system[J].Acta Math Sinica: Chinese Series, 2010, 53(4)：751-758.

[10] BRUCK R E. Nonexpansive projections on subsets of Banach spaces[J].Pacific J Math,1973,47:341-355.

[11] XU Hongkun.Inequalities in Banach spaces with applications[J].Nonlinear Anal, 1991,16:1127-1138.

[12] XU Hongkun. An iterative approach to quadratic optimization[J].J Optim Theory Appl,2003,116:659-678.