一种简单的加权整体最小二乘直线拟合方法

王继刚，周 立，蒋廷臣，孙佳龙

(淮海工学院 测绘学院，江苏 连云港 222005)

一、引 言

道路桥梁工程、工业测量拟合、GIS数据采集和变形监测分析与预报等测量数据处理工作中直线拟合有着广泛的应用。常规方法是测定直线上若干点，列立误差方程式时只顾及因变量误差，依据最小二乘准则获得拟合方程。由于忽略了自变量误差，导致拟合方程中存在着一定的模型误差。若要克服模型误差，应利用整体最小二乘法来求解直线的斜率和截距。文献[1—4]较为详细地探讨了顾及因变量误差的直线拟合问题，但这些文献存在的问题是：要么未彻底解决模型误差问题，要么模型仅仅适用于等精度观测。事实上，在实际应用中，直线坐标分量观测精度可能不等，这时应使用加权整体最小二乘法拟合。沈云中等[5-8]提出了严密的加权整体最小二乘直线拟合模型，虽然这些模型精度高，但算法往往涉及复杂的矩阵理论，运算过程繁琐，不利于广大一线测绘工作者理解和应用。

实际上，在不等精度直线拟合模型中，有两个问题待解决：① 同时考虑坐标分量的误差和观测精度；② 所建立的直线方程是否是唯一的。无论哪种坐标分量是因变量，也无论直线方程系数近似值是如何得到的，最终得到的拟合方程都是一样的。本文通过对直线拟合模型的深入分析，从广大测绘工作者熟悉的测量平差角度入手，运用附有参数的条件平差理论建模，拟解决上述两个问题，将不等精度的整体最小二乘法直线拟合纳入到测量平差方法范畴，为进一步研究加权整体最小二乘拟合模型打下了基础。

二、拟合模型

设某一条待定直线上某点i观测值为(xi,yi)，i=1,2,…,n，其对应的观测误差分别为εxi和εyi，那么坐标分量之间存在的关系可表述为

a(x+εxi)+b(y+εyi)=c

(1)

式中，a和b为待估参数；c为由相关关系确定的常数，此处可设为1。

考虑到待估参数受到观测误差的影响，不妨取a=a0+δa和b=b0+δb，a0和b0分别为a和b的近似值，δa和δb分别为对应的改正数。将式(1)展开并略去二次项，得线性近似表达式为

a0vxi+b0vyi+xiδa+yiδb+a0xi+b0yi=1

(2)

式中，vxi和vyi为对应误差εxi和εyi的估计值。现有n个观测值，存在着n个观测方程，用矩阵形式可表述为

在测量数据处理中，采用赋权方法处理不等精度观测问题，由加权最小二乘准则

VTPV=min

(4)

来求解式(3)。其中，权阵P为2n阶方阵，权阵本质是一种先验精度矩阵。当所有的坐标分量都是独立观测得到的，此时P为对角阵；更特殊的是所有坐标分量都是独立等精度观测得到的，此时P为单位阵。

实际上式(3)是一个附有参数的条件平差问题，与附有参数的条件平差问题略有差异，其秩R(B)=2，参数的个数等于待估计的参数个数，但这不影响估计结果。从平差模型本质上看，间接平差和条件平差模型都可以看成附有参数的条件平差的特例，附有参数的条件平差模型是无法用间接平差或条件平差模型所表述的狭义模型。

根据附有参数的条件平差模型求解参数估值和精度评定方法，易得参数估值、单位权方差估计及平差参数的协方差阵，现直接给出相关结果如下，具体推导和有关符号含义参见文献[9]。

特别的，当P为单位阵时，式(5)和式(7)可分别简化为

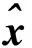
三、实例计算

本文采用一个经典的不等精度的直线拟合算例进行分析，具体数据见表1。文献[5—8]均运用该算例验证了加权整体最小二乘法的有效性。算例中共有10个样本点，每一个样本点的坐标分量观测精度用权加以量化。

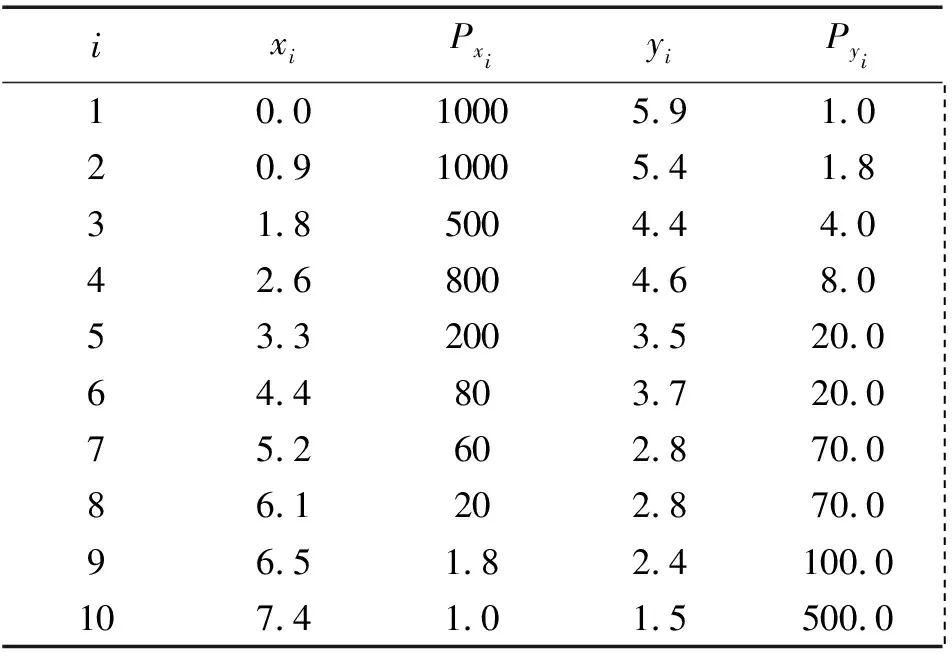
表1 观测值样本

对于表1中的数据，用常规的加权拟合法无法同时使用x和y两坐标分量的权，而如果仅仅采用x或y的权，得到的结果误差较大，甚至严重地背离了真值，直接影响了拟合结果的应用，几种拟合方法计算结果见表2。

表2 几种方法计算结果比较

在采用本文模型时，可认为每个坐标分量都是独立观测得到的，即权阵P为对角阵。首先分析等精度的情况，即忽略坐标分量观测精度，取P为20阶单位阵，计算得到直线的斜率和截距与严密模型矩阵分解法(Golub算法)所得结果完全一致，表明本文建模方法是正确的。

对于加权模型，因为获取近似值的3种方法(即x为自变量、y为自变量和等精度模型)得到的a0和b0相差很大，必须采用迭代算法。本文阈值设置为10-5，对于这3种方法获得的近似值，最多迭代5次后就都收敛到了同一数值，表明本算法稳定，不受近似值的影响，解决了用不等精度直线拟合模型中存在的两个问题。

从表2可以看出，本文的结果与真值和严密算法相比还存有微小的误差，用向量的2-范数来衡量相对误差，该方法计算结果的相对误差仅有2%，完全能满足一般工程计算的精度要求。表明本文所提出的加权拟合模型误差小，进一步证明了建模方法的正确性。

四、结束语

在深入分析直线拟合误差模型的基础上，本文基于附有参数的条件平差理论建模，得到了一种简单的加权整体最小二乘直线拟合模型。该模型解决了不等精度直线拟合中存在的两个问题，同时将加权整体最小二乘直线拟合模型纳入到测量平差体系中，模型算法简单且稳定、占机时间少、计算误差小，不涉及诸如矩阵分解和Kronecker积运算等复杂的矩阵理论，非常有利于广大一线测绘工作者的应用。对于解决目前遇到的许多新问题具有一定的参考价值，对进一步研究顾及系数矩阵误差的整体最小二乘解具有一定的启发，为今后更深入地研究加权整体最小二乘在测绘中的应用打下了一定的基础。

参考文献：

[1] 王安怡，陶本藻. 顾及自变量误差的回归分析理论和方法[J]. 勘测科学技术，2005(3)：29-32.

[2] 刘大杰，史文中，童小华，等. GIS空间数据的精度分析与质量控制[M]. 上海: 上海科学技术文献出版社, 1999.

[3] 鲁铁定，陶本藻，周世健. 基于整体最小二乘法的线性回归建模和解法[J].武汉大学学报：信息科学版，2008,33(5)：504-507.

[4] 丁克良，沈云中，欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学：自然科学版，2010,29(1)：44-47.

[5] SHEN Y, LI B, CHEN Y. An Iterative Solutin of Weighted Total Least-squares Adjustment [J].Journal Geodesy, 2011,85(4)：229-238.

[6] NERI F, SAITTA G, CHIOFALO S. An Accurate and Straightforward Approach to Line Regression Analysis of Error-affected Experimental Data [J]. Journal Physics E: Scientific Instruments, 1989,22(4)：215-217.

[7] SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Liner Regression [J].Journal Geodesy, 2008,82(7)：415-421.

[8] AMIRI-SIMKOOEI A, JAZAERI S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodetic Science，2012，2(2)：113-124.

[9] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M].2版. 武汉:武汉大学出版社,2009：96-103.