改进型负输入整形与最优控制结合的振动抑制方法

赵志刚， 游斌弟， 赵 阳

(1.中国民航大学 空中交通管理学院，天津 300300；2.哈尔滨工业大学 航天学院，哈尔滨 150001；3.哈尔滨工业大学 (威海)船舶与海洋工程学院,山东 威海 264209)

改进型负输入整形与最优控制结合的振动抑制方法

赵志刚1,2， 游斌弟3， 赵 阳2

(1.中国民航大学 空中交通管理学院，天津 300300；2.哈尔滨工业大学 航天学院，哈尔滨 150001；3.哈尔滨工业大学 (威海)船舶与海洋工程学院,山东 威海 264209)

针对诸如柔性机械臂这类柔性系统的主动振动控制问题，提出了基于改进型负输入整形和最优控制结合的振动抑制方法。以柔性机械臂为研究对象，设计最优状态反馈控制实现其旋转机动任务及柔性振动抑制。为增强柔性振动抑制效果和改善系统的运动时间，根据引入线性二次型调节器(LQR)反馈后整个闭环系统的振动频率和阻尼比设计改进型负输入整形器作为前馈控制器。将前馈控制与反馈控制相结合能发挥其各自的优点，提高系统的性能。仿真分析结果表明，所设计的混合控制策略可以有效地抑制柔性振动，且可以减少系统响应时间的延迟和加快系统响应速度。

主动振动控制；改进型负输入整形；最优控制；线性二次型调节器；柔性机械臂；振动抑制

现代工业和航空航天等领域广泛应用柔性结构来满足轻型化、柔性化的设计要求。其中，柔性机械臂(如高空作业车的伸缩臂，空间机械臂等)作为一种典型代表常用来完成各种作业任务。然而，柔性机械臂在执行操作任务时容易产生振动，影响其定位精度和工作效率，严重时甚至危害机械臂系统结构的安全。解决柔性机械臂的柔性振动抑制问题可以提高其工作性能，增强系统的安全性和可靠性，并且可以降低系统的操作成本。因此，这一课题具有重要的工程意义，已引起了国内外许多研究者的兴趣。

针对柔性结构的振动抑制问题，国内外学者提出了许多种研究方法[1-2],如最优控制、自适应控制、鲁棒控制、奇异摄动控制、模糊控制、滑模控制等，上述方法及其复合控制方法等获得了较深入的研究。其中，最优控制是通过求解最优控制力来使系统振动达到理想的抑制效果，且兼顾响应与控制两方面相互矛盾的要求，是满足一定最优条件的反馈控制。对于具有二次型性能指标的线性系统，因其最优反馈控制律能用解析的形式表示，易于工程实现，历来受到人们的重视。戈新生等[3]针对双连杆空间刚柔性机械臂的残余振动问题，采用LQ最优控制方法来消除残余振动，通过数值仿真表明所提出方法的有效性。

除了上面列举的控制方法之外，还有一种越来越吸引人们兴趣的主动振动控制方法——输入整形(Input Shaping，IS)(又称为输入成形或输入成型)振动抑制方法。该方法作为一种典型的前馈控制方法，自从Singer等[4]正式提出以来就得到了广泛而深入的研究。近年来，国内学者在此领域也取得了丰富的研究成果。董明晓等[5]设计最优输入整形器(Input Shaper)，应用于变参数桥式起重机等的防摆控制中。张鹏等[6]通过引入偏值点，提出了基于零点配置技术的EI成型器设计方法。输入整形作为一种简单、高效的前馈补偿器与反馈控制相结合时，不仅可以提高控制性能，甚至还可以降低反馈控制器的设计难度。胡庆雷等[7-10]将输入成形方法与滑模变结构控制相结合应用于挠性航天器大角度姿态机动时挠性结构的振动控制。Pai[11]提出了输入整形结合自适应滑模控制的方案解决带有参数不确定性和外扰的柔性结构振动控制问题。孔宪仁等[12]将输入成形和PD反馈控制器相结合来解决柔性航天器的振动抑制问题。李瑞川等[13]将PD控制结合输入整形控制策略应用到含有刚性模态的弹性机构中，研究了输入整形参数对系统控制力的作用规律以及降低系统能耗的机理。王晓军等[14]研究了输入整形技术结合线形二次型调节器(LQR)的混合控制方案来解决桥式起重机这一类不完全控制系统的负载残留振荡抑制问题。上述研究所取得的成果大多都是基于传统的输入整形设计方法，陕晋军等[15]通过放宽设计整形器需满足包含最少脉冲个数的约束，提出了改进型的输入成形方法(Modified Input Shaping, MIS)并应用该方法结合PD控制用于柔性机械臂的振动抑制，理论分析表明在一些方面比传统的输入成形方法有更好的性能。输入整形法能够很好地抑制柔性系统振动所付出的代价是系统运动响应时间的延迟，为了获得更快的运动响应，可以通过在输入整形器脉冲序列中引入负脉冲来提高系统的上升时间。

综上所述，为进一步提高控制效果、改善控制系统性能，尤其是提高系统上升时间，本文提出改进型负输入整形控制和最优状态反馈控制相结合的控制方法。首先设计LQR反馈控制器，然后设计改进型负输入整形器作为前馈控制器，构成前馈控制和反馈控制的混合控制方案来解决柔性结构的振动抑制问题。

1 输入整形

输入整形是指由一系列脉冲序列与一定的期望输入相卷积，所形成的指令作为控制系统运动的输入。其中，根据振动系统频率和阻尼比所设计的脉冲序列称之为输入整形器[2]。其成形过程如图1所示。

图1 输入整形器对输入信号进行成形Fig.1 The input shaping process

为研究输入整形方法，考虑单自由度有阻尼二阶振动系统：

(1)

式中：ω为系统自然振动频率，ζ为系统阻尼比。

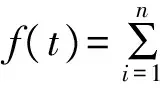
(2)

其中：

(3)

(4)

为使成形后的指令可以使系统达到与原控制指令相同的运动位置，还需要脉冲幅值约束条件，即

(5)

此外，整形器的时间长度越短，给系统带来的时间滞后就会越短，有利于提高系统的响应速度。因此，时间约束条件为

min(tn)

(6)

根据式(2)至式(6)，对于确定的系统，已知其自然频率ω和阻尼比ζ，就可根据残余振动V(ω,ζ)的值为零或低于某一期望水平来确定脉冲幅值Ai和作用时间ti。

1.1 典型输入整形器

传统最简单的正输入整形器是包含两脉冲的整形器，称之为ZV(Zero Vibration)整形器[4]，其数学表示形式为

(7)

其中KT、Td表示如下式

(8)

满足约束条件式(2)-式(5)，并在同一振动周期内选择多个脉冲可以获得MIS ZV整形器[15]，对于3脉冲MIS ZV整形器可表示如下：

(9)

其中KM表示如下式

(10)

1.2 改进型负输入整形

设计输入整形器的关键在于确定脉冲序列中各脉冲的幅值和作用时间。除此之外，确定整形器中所包含的脉冲个数也至关重要。本文给出一种改进型负输入整形(Modified Negative Input Shaping，MNIS)方法，该方法放宽整形器包含最少脉冲个数的约束，且在同一振动周期内选择包含正负交替的脉冲。

满足约束条件式(2)为零，即保证系统残余振动为零，且同时满足式(5)的MNIS ZV整形器的脉冲作用时间选择为

(11)

式中：n为整形器脉冲序列所包括脉冲个数。式(11)同时表明：随着脉冲个数的增加，每个脉冲可以获得更短的延迟时间。

与脉冲作用时间式(11)相对应的脉冲幅值为

(12)

式中：

(13)

M=-K+…+(-1)i-1Ki-1+…+(-1)n-1Kn-1=

(14)

式(11)-式(14)给出了改进型负输入整形器的封闭解，根据以上内容，只要知道系统的振动频率与阻尼比以及所确定的脉冲数目，就可以很方便地设计MNIS ZV整形器。通过该方法所设计的整形器可以得到更短的延迟时间，且脉冲序列中所包含的脉冲个数可以灵活选择。这给研究人员在实际工程设计中留有更多的选择空间。例如，对于3脉冲MNIS ZV整形器，可表示如下：

(15)

式中：

(16)

2 线性二次型最优控制

LQ最优控制因其产生状态线性反馈的最优控制律，易于构成闭环最优控制，对从事主动振动控制的研究人员具有很大吸引力，在工程中得到了广泛应用。

LQR最优控制是要求在满足动力学方程

(17)

且能使系统在消耗较少控制能量的情况下，确定最优控制输入u*，使下面二次型性能指标Jm最小。

(18)

式中：Q是对状态变量加权矩阵，为半正定对称矩阵；R是对控制变量加权矩阵，为正定对称矩阵。

LQR最优控制问题就是对线性时不变系统式(18)确定最优控制的输入规律，即

其实，我和阿花也是老朋友了，阿花当年从韶关来深圳时,我们就认识了。林强信将雪茄掐在烟灰缸里，说，我们曾有过多次合作，而且很愉快。所以你去她厂里，我赞成。你帮她，就等于我在帮她嘛。哈哈哈……

u=-Kx

(19)

式中：K为状态反馈增益矩阵。

利用极值原理，使得二次型性能指标式(19)最小的K表示为

K=R-1BTP

(20)

其中：P为正定对称常数矩阵，满足下列Riccati代数方程

ATP+PA-PBR-1BTP+Q=0

(21)

由式(19)和式(20)，则可得LQR最优控制为

u*=-R-1BTPx

(22)

3 柔性机械臂系统

以柔性机械臂作为被控对象进行应用研究，仿真模型如图2所示。柔性机械臂系统由中心刚体、柔性臂杆及末端刚性负载mp组成。图2中OXY和Oxy分别是惯性坐标系和柔性臂体固联坐标系，Ox与未变形时柔性臂的轴线重合，其原点位于臂与中心刚体的连接处，θ(t)表示两坐标系间的相对转动关系。柔性臂相对坐标系Oxy的柔性变形用δ表示。l,ρ,E,φ,Φ分别表示柔性臂长度、密度、弹性模量、内外圆直径。Jo表示中心刚体转动惯量。

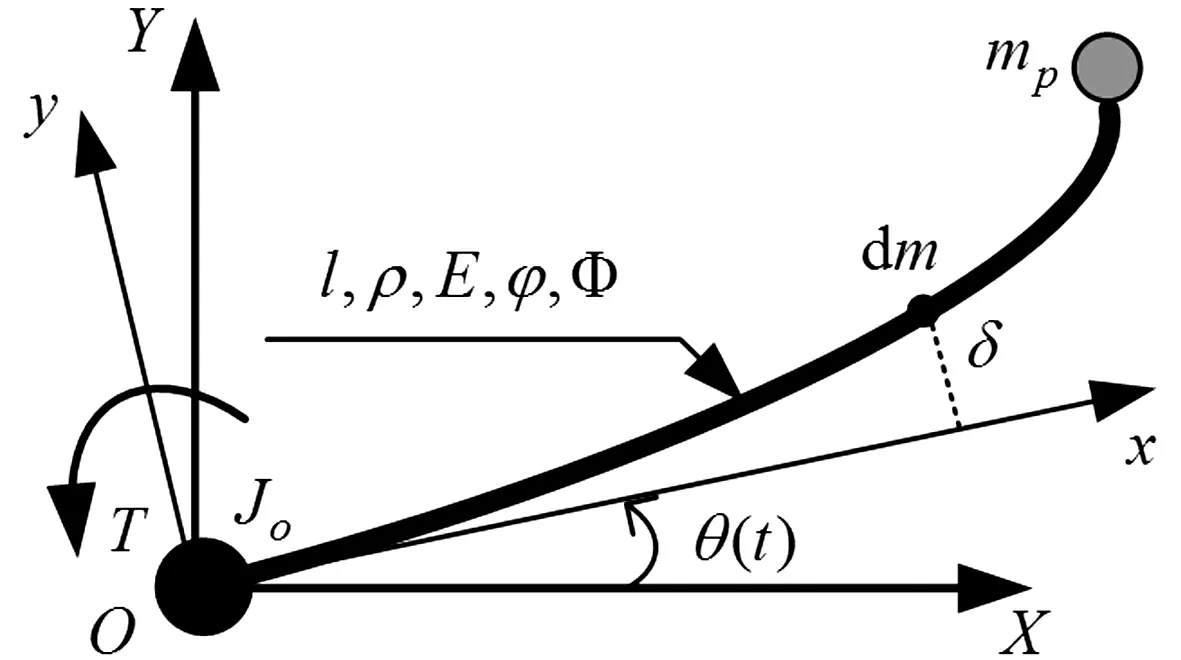
图2 柔性机械臂的简化模型Fig.2 Sketch of the flexible manipulator model

应用有限元法描述系统的弹性变形，采用拉格朗日方法建立系统的动力学方程，可得由系统广义自由度θ和节点位移列阵d表征的动力学方程:

(23)

式中：J为系统总转动惯量；I为刚柔耦合矩阵；M为柔性臂质量阵；C为柔性臂阻尼阵；K为柔性臂刚度阵；T为驱动力矩。

利用约束模态法展开式(23)，可得柔性臂运动与振动耦合的动力学方程如下：

(24)

式中：ωc=diag(ωc1,…,ωcN)和ζ分别表示约束模态频率矩阵和阻尼比矩阵；ηc=[ηc1,…,ηcN]T为约束模态坐标向量；Hc为1×N维的模态坐标耦合矩阵，EN为N×N维单位阵，N表示约束模态截断阶数。

4 改进型负输入整形与LQR联合设计

则可以将式(24)写为

(25)

式中：E为相应维数的单位阵。

即可得状态空间的形式方程

y=CX

(26)

其中：

Bc=[0 0 1 0]T,C=[1 0 0 0]

进一步改写为如下状态方程的形式

y=CX

(27)

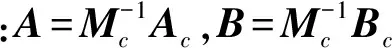
本文提出的改进型负输入整形控制和最优状态反馈控制相结合方法主要分为以下两个步骤：

第一步，设计最优状态反馈控制律，实现柔性机械臂旋转机动任务的同时对柔性振动进行抑制。

将式(22)代入式(27)，可得闭环系统的状态方程为

y=CX

(28)

式中：As=A-BR-1BTP为闭环系统矩阵。

第二步，根据整个闭环系统的特征值设计改进型负输入整形器，输入形成器的控制作用在LQR反馈回路的前端，目的是在保证被控对象完成旋转机动任务的同时进一步抑制其柔性振动。

闭环系统矩阵As的特征值，可求出系统模态的振动频率和阻尼比

(29)

其中：λsi为矩阵系统矩阵As的第i个特征值，ωsi和ζsi分别为系统模态的振动频率和阻尼比。

基于改进型负输入整形与LQR联合设计实现机械臂振动抑制的原理如图3所示。

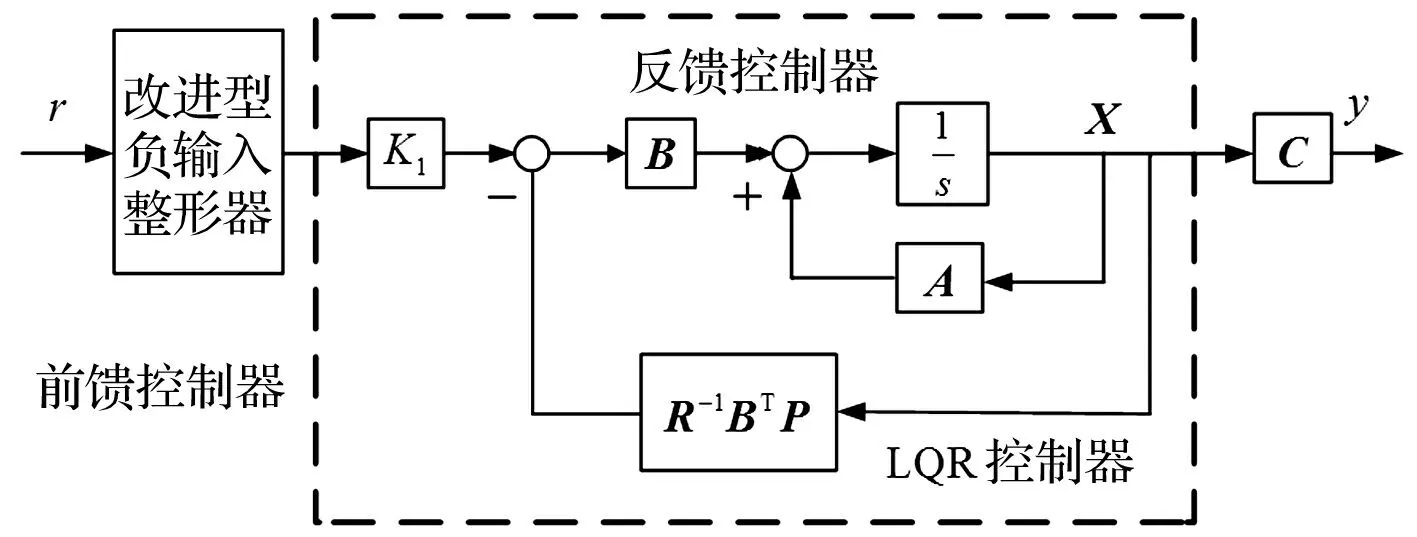
图3 实现振动抑制的控制系统原理框图Fig.3 Block diagram of control system for vibration suppression

其中：r为期望输入，K1取决于状态反馈增益K=[K1K2…K2(N+1)]中对应的角位移反馈系数。

根据式(29)中闭环系统振动模态的振动频率ωsi和阻尼比ζsi可以灵活设计一系列包含不同脉冲个数的MNIS整形器，使机械臂在改进型负输入整形器和LQR控制器联合控制下完成指定旋转任务，同时实现振动抑制。

当然，实际情况中受控对象一般包含多阶振动模态，这就需要设计多模态整形器。多模态系统的输入整形器设计方法一般有联立方程法[16]和级联法[4]。考虑到前者的计算相当复杂，往往需要借助专门的计算软件进行求解和设计，而后者设计简单，且对高模态的不灵敏性要比前者更高，所以本文应用级联法实现多模态整形器的设计，即采用如下的卷积形式来获得：

Smj=S1*S2*…*Si*…*SN

j=1,2,…,N

(30)

其中“*”表示进行卷积运算处理，Si代表对应系统第i个振动模态的输入整形器。

5 仿真算例

为了进一步验证本文所提出的MNIS整形器的有效性，系统主要仿真参数：转动惯量Jo=40 kg·m2，臂杆长度l=4 m，材料密度ρ=2 700 kg/m3，弹性模量E=70 GPa，外圆直径Ф=0.03 m，内圆直径φ=0.028 m，负载质量mp=2 kg。有限单元体个数n=10，初始状态为零。为了对比分析仿真效果，应用LQR控制器结合不同输入整形器设计了四种控制方案完成参考输入为60°机械臂旋转机动任务，详见表1。

表1 四种控制方案

考虑到系统存在刚体运动振动和柔性模态振动，这里抑制刚体运动模态(ωr=0.337 2 rad/s，ζr=0.706 0)和一阶柔性系统模态(ωf=5.517 7 rad/s，ζf=0.023 5)，采用级联法进行设计。首先为刚体运动的振动模态设计相应的整形器Sr，然后为柔性模态振动设计相应的整形器Sf。根据式(30)，将获得的整形器进行级联，可得一个新的整形器Sm=Sr*Sf，以实现同时对刚体运动的振动和柔性模态振动的振动抑制。为便于比较，四种控制方案中LQR均取相同反馈增益，K=[10.00 0.025 3 41.96 1.749]，K1=10.00(取LQR反馈中x1的增益)；所用各种整形器参数如下：

i=1,2

(31)

i=1,2,3

(32)

i=1,2,3

(33)

四种方案的仿真结果如图4-图9所示，分析其控制效果如下：

四种方案均有效地完成了柔性机械臂的旋转60°机动任务。由图4-图9可以看出，单独采用LQR控制的方案1能够实现机动任务，所用上升时间约为9.87 s，但是存在超调量，调整时间大约为23 s；而且存在残余振动，一阶模态振动持续时间约30 s，机械臂末端弹性变形也较大，难于迅速精确定位于期望的位置。而引入整形器的方案2和方案3刚体运动都非常平稳，没有超调量，所用上升时间分别约为13.7 s和18.3 s。这说明LQR通过和输入整形技术结合，产生的混合方案能够有效地减小机械臂的振动，但由于整形器时滞时间的存在而增加了系统的上升时间。为了降低这种不利影响，方案4基于改进型负输入整形与LQR联合控制使刚体运动非常平稳，没有超调量，且柔性振动模态抑制效果也很好。所用上升时间约为9.15 s。

方案2、方案3和方案4与方案1相比，由于输入整形器的作用使得角速度曲线变得比较光滑，角速度变化更平稳，如图6所示。方案4与方案2相比虽然所用整形器包含脉冲个数多，但是由于负脉冲的引入，仍然有更短的上升时间，减少了4.55 s；方案4的上升时间仅为方案3的一半，大大减少了正输入整形器导致的系统响应的时间延迟，这说明了方案4在改善机械臂运动时间上比方案2和方案3具有较大优越性。

综上所述，仿真实验结果表明改进型负输入整形器和LQR控制器联合控制方案使机械臂在下完成指定的旋转任务的同时有效抑制了柔性振动，且在减少系统响应延迟时间、提高了工作效率上优于LQR控制器和其它输入整形器组成的方案。

图4 控制输入指令Fig．4Controlinputcommand图5 角位移Fig．5Angulardisplacement图6 角速度Fig．6Angularvelocity

图7 一阶模态坐标Fig．7Thefirstmodalcoordinate图8 末端弹性变形Fig．8Deformationangleoftip图9 末端弹性变形速度Fig．9Deformationvelocityoftip

6 结 论

以柔性机械臂为研究对象，提出了基于改进型负输入整形主动振动控制和最优控制相结合的控制器设计方法来解决诸如柔性机械臂这类柔性系统的振动抑制问题，具体工作及结论如下：

(1) 为完成柔性机械臂旋转机动任务，以消耗较少控制能量为性能指标设计LQR反馈控制器，并同时进行振动抑制；

(2) 为进一步改善控制效果、提高系统响应速度，根据LQR反馈后的整个闭环系统的振动频率和阻尼比设计改进型负输入整形器，应用级联法设计刚体运动振动和柔性模态振动的多模态整形器作为前馈控制器，进行振动抑制；

(3) 对比文中设计的四种控制方案：改进型负输入整形器和LQR控制器联合控制的方案增强了振动抑制效果，有效减小系统响应超调量，在改善机械臂的运动时间，提高工作效率上优于LQR控制器和其它输入整形器组成的方案；

(4) 进一步工作重点是将本文方法应用于柔性结构振动抑制试验研究中。此外，如果系统的转动惯量等参数的实际值和名义值不同，即模型参数不精确，这将影响系统的频率和阻尼比信息的获得。根据不精确信息设计的整形器可能会导致系统残余振动不能被完全消除，这就需要设计具有鲁棒性的改进型负输入整形器来解决此问题，这也是进一步要研究的问题。

[ 1 ] Benosman M, Vey G L. Control of flexible manipulators: A survey[J]. Robotica, 2004, 22(5), 533-545.

[ 2 ] 王树新, 员今天, 石菊荣, 等. 柔性机械臂建模理论与控制方法研究综述[J]. 机器人, 2002, 24(1), 86-91, 96. WANG Shu-xin, YUAN Jin-tian, SHI ju-rong, et al. A roadmap of research on modeling and control strategy for flexible manipulators[J]. Robot, 2002, 24(1), 86-91, 96.

[ 3 ] 戈新生, 姜兵利, 刘延柱．空间刚柔性机械臂振动抑制的LQ最优控制方法[J]. 振动与冲击, 1999, 18(1)：49-52, 56. GE Xin-sheng, JIANG Bing-li, LIU Yan-zhu. The LQ optimal control method for vibration suppression of rigid flexible space manipulator[J]. Journal of Vibration and Shock, 1999, 18(1): 49-52, 56.

[ 4 ] Singer N C, Seering W P. Preshaping command inputs to reduce system vibration[J]. Journal of Dynamics Systems, Measurement and Control, 1990, 112(3): 76-82.

[ 5 ] 董明晓, 脱建智, 任意翔, 等. 最优输入整形抑制变参数桥式起重机载荷摆动[J]. 振动与冲击, 2009, 28(10): 207-209. DONG Ming-xiao, TUO Jian-zhi, REN Yi-xiang, et al. Optimal input-shaper to suppress payload oscillation of bridge cranes with varying parameters[J]. Journal of Vibration and Shock, 2009, 28(10): 207-209.

[ 6 ] 张鹏, 李元春. 基于混合EI成型器的多模态柔性结构振动控制[J]. 力学学报, 2010, 42(4): 774-781. ZHANG Peng, LI Yuan-chun. Vibration control of multi-mode flexible structure based on hybrid extra-insensitive shaper[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 774-781.

[ 7 ] 胡庆雷, 马广富.基于滑模输出反馈与输入成形控制相结合的挠性航天器主动振动抑制方法[J]. 振动与冲击, 2007, 26 (6):133-138, 189. HU Qing-lei, MA Guang-fu. Active vibration suppression in flexible spacecraft with mismatched uncertainty via sliding mode/shaped input control[J]. Journal of Vibration and Shock, 2007, 26 (6):133-138, 189.

[ 8 ] HU Qing-lei, SHI Peng, GAO Hui-jun. Adaptive variable structure and commanding shaped vibration control of flexible spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 804-815.

[ 9 ] HU Qing-lei, MA Guang-fu. Active vibration suppression in flexible spacecraft attitude maneuver using variable structure control and input shaping technique[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California, Aug. 15-18, AIAA, 2005：2005-6246.

[10] HU Qing-lei. Input shaping and variable structure control for simultaneous precision positioning and vibration reduction of flexible spacecraft with saturation compensation[J]. Journal of Sound and Vibration, 2008, 318 (1-2): 18-35.

[11] Pai M C. Closed-loop input shaping control of vibration in flexible structures via adaptive sliding mode control[J]. Shock and Vibration, 2012, 19(2): 217-229.

[12] 孔宪仁, 杨正贤, 叶东, 等.基于输入成形的柔性航天器振动闭环抑制方法研究[J]. 振动与冲击, 2010, 29(3): 72-76.

KONG Xian-ren, YANG Zheng-xian,Ye Dong, et al. Feedback control in conjunction with input shaping for flexible spacecraft vibration suppression[J]. Journal of Vibration and Shock, 2010, 29(3): 72-76.

[13] 李瑞川, 徐涛, 左文杰, 等. 基于PD结合输入整形控制的含有刚性模态弹性机构的力及能耗分析[J]. 振动与冲击, 2010, 29(12): 158-161. LI Rui-chuan, XU Tao, ZUO Wen-jie, et al. Analysis on force and energy consumption for elastic mechanisms with a rigid mode motion based on PD combined with input-shaping control[J]. Journal of Vibration and Shock, 2010, 29(12): 158-161.

[14] 王晓军, 邵惠鹤. 基于输入整形的线性二次型调节器及其应用[J]. 上海交通大学学报, 2006, 40 (5): 848-851, 855. WANG Xiao-jun, SHAO Hui-he. The linear quadratic regulator based on input shaping technique and its application[J]. Journal of Shanghai Jiaotong University, 2006, 40 (5): 848-851, 855.

[15] Shan J J, Liu H T, Sun D. Modified input shaping for a rotating single-link flexible manipulator[J]. Journal of Sound and Vibration, 2005, 285(1-2): 187-207.

[16] Hyde J M, Seering W P. Inhibiting multiple mode vibration in controlled flexible systems[C]. American Control Conference. Boston: IEEE, 1991: 2449-2454.

Combination of modified negative input shaping and optimal control for vibration suppression

ZHAO Zhi-gang1,2, YOU Bin-di3, ZHAO Yang2

(1.College of Air Traffic Management, Civil Aviation University of China, Tianjin 300300, China;2. School of Astronautics，Harbin Institute of Technology， Harbin 150001，China; 3. School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China)

A new vibration reduction control strategy was presented. With it, the modified negative input shaping (MNIS) technique was combined with the optimal control method for active vibration control of flexible systems, such as, a flexible manipulator. An optimal state feedback controller was designed for the flexible manipulator maneuver and its vibration eliminating. To improve the performance of vibration control and reduce the system response time duration, a modified negative input shaper was used as a feed-forward controller, it was designed to utilize the vibration frequency and damping ratio of the whole closed loop system with a linear quadratic regulator (LQR). Combining the feed-forward control and feedback control and utilizing the respective advantages, the performance of the control system can be improved. Both analytical and numerical results were presented to demonstrate the effectiveness of the hybrid control strategy. It was shown that the proposed method can be used to reduce the time delay of the system’s response and increase the response speed of the system.

active vibration control; modified negative input shaping (MNIS); optimal control; linear quadratic regulator (LQR); flexible manipulator; vibration suppression

国家重点基础研究发展计划(973计划)项目(2013CB733000);国家自然科学基金资助项目(50975056，11072066);国家青年科学基金资助项目(51205079)

2012-12-06 修改稿收到日期：2013-03-23

赵志刚 男，博士生, 1982年生

V414; TP271

A

10.13465/j.cnki.jvs.2014.08.035