弹性地基上受切向力作用梁稳定性研究

李 威, 曾志松, 韩 旭

(1.华中科技大学 船舶与海洋工程学院，武汉 430074；2.湖南大学 机械与运载工程学院，长沙 410082;3.船舶与海洋水动力 湖北省重点实验室，武汉 430074)

弹性地基上受切向力作用梁稳定性研究

李 威1,3, 曾志松1, 韩 旭2

(1.华中科技大学 船舶与海洋工程学院，武汉 430074；2.湖南大学 机械与运载工程学院，长沙 410082;3.船舶与海洋水动力 湖北省重点实验室，武汉 430074)

用广义微分求积法(GDQR)分析了弹性地基上复杂弹性支承条件下受切向力作用梁的稳定性问题。基于弹性支承梁的运动微分方程及边界条件，采用GDQR进行离散化，获得由动力方程组及边界条件合成的特征值矩阵方程。通过对相应特征值方程的具体分析，讨论了弹性地基模量、剪切系数、复杂边界条件对临界载荷的影响，研究了一端固定约束、另一端弹性约束梁弹性失稳区域随弹性地基模量和支承弹簧刚度变化的情况，得到了一些有益的结论。结果表明：GDQR能很好地解决此类系统的稳定性问题。

广义微分求积法；稳定性；弹性地基；切向力

弹性地基上复杂支承条件下梁的稳定性问题，具有较高的学术研究价值以及广泛的工程应用背景。许多学者已经对弹性地基上不同边界条件下梁的稳定性问题进行了研究，Smith等[1]研究了弹性地基上受随从力作用梁的稳定性问题，发现Winkler弹性地基模量对切向力作用下悬臂梁的临界颤振失稳载荷没有影响；Lee等[2-3]研究了弹性地基上梁的稳定性问题，发现剪切系数增强或者减弱梁的稳定性取决于弹性地基模量、支承条件等因素；马小强等[4]运用传递矩阵法研究了弹性地基上任意支承输液管的稳定性，计算了其临界流速；包日东等[5]用微分求积法讨论了水下弹性支承管道的动力特性，发现弹性支承条件对系统的动力特性影响很大。然而，以往的研究更多的是基于刚性约束边界条件，对于弹性地基上更为复杂边界条件、受剪切力作用下梁稳定性的讨论则比较少。

广义微分求积法(GDQR)是求解微分方程边值、初值问题的有效的数值计算方法，已经成功地用于许多力学问题的求解[6-10]，其替代规则中采用的独立变量不仅包括各网点处的函数值，而且包括函数的导数项，克服了微分求积法需要在边界点处选取微小段来进行边界的邻接处理，能够精确的施加边界条件，因而简单易行，具有较高的精确度和数值稳定性。本文将GDQR应用到弹性地基上受切向力作用复杂弹性支承梁的稳定性问题中，对于一端固定约束、一端支承弹簧约束梁，研究了弹性地基模量对梁临界载荷随剪切系数变化的影响，讨论了在一定Winkler弹性地基模量、不同支承弹簧刚度下，临界载荷随剪切系数的变化规律；而针对一端固定约束、一端扭转弹性约束梁，则分析了不同扭转弹簧刚度下，临界载荷随剪切系数的变化情况；最后研究了Winkler 弹性地基模量和支承弹簧刚度对一端固定约束、另一端弹性约束梁弹性失稳区域的影响。

1 运动微分方程及边界条件

考虑如图1所示的弹性地基上两端弹性支承均匀梁受剪切力作用，假定W(X,t)=w(X)eiωt,M*(X,t)=M(X)eiωt,Q*(X,t)=Q(X)eiωt,W、M*、Q*分别代表弯曲变形、弯矩、剪力，i=(-1)1/2,ω代表梁振动的角频率。对于弹性地基本文采用Winkler弹性地基模型。

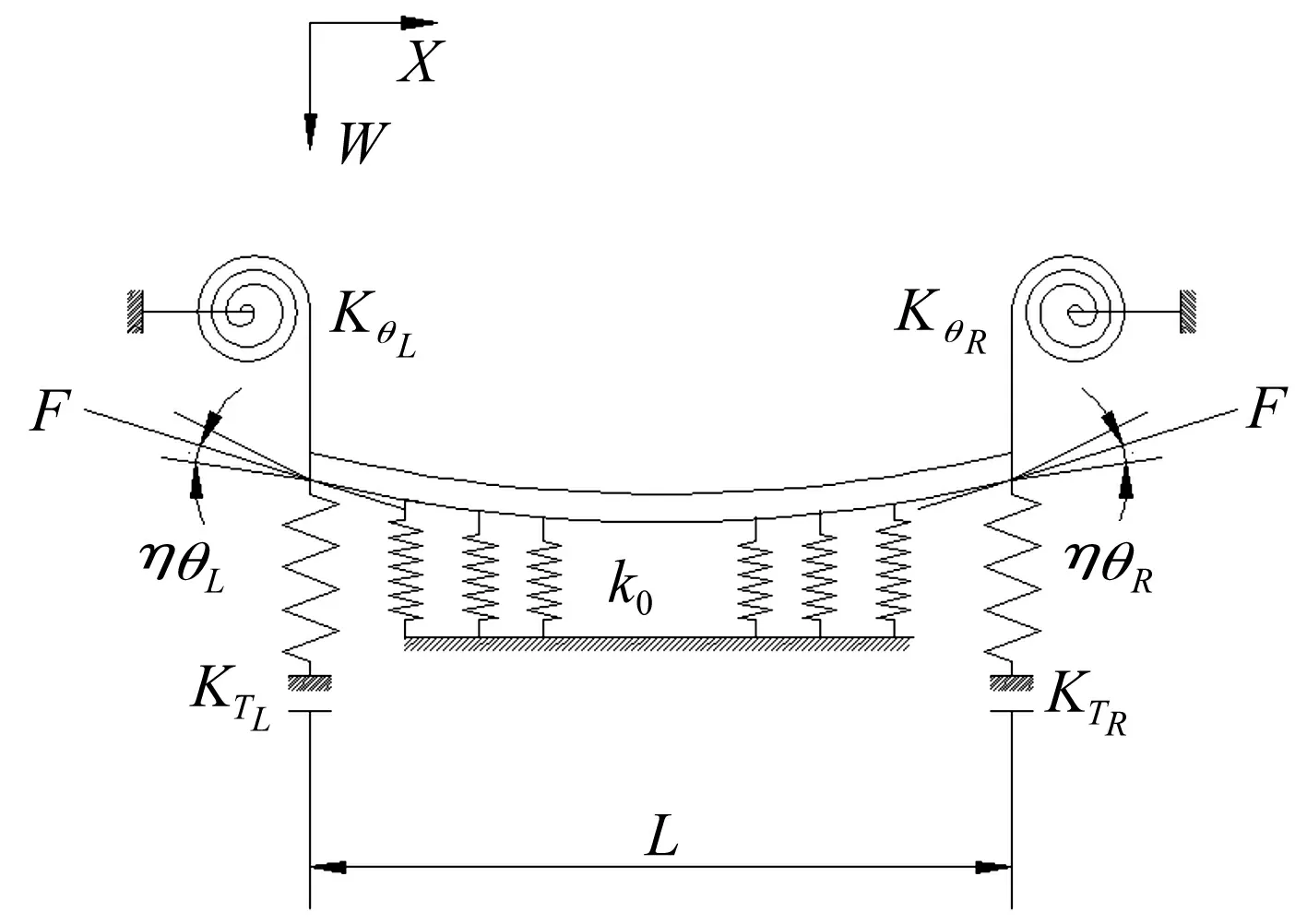
图1 系统模型简图Fig.1 Geometry of the system

引入无量纲量：

E表示杨氏模量，I表示梁截面惯性矩，F为剪切力，η表示剪切系数，m表示梁单位长度质量，L表示梁长度，k0表示Winkler 弹性地基模量，KθL，KTL，KθR，KTR分别表示左右两端面的扭转弹簧刚度、支撑弹簧刚度。θL，θR表示左右两端转角。

上述梁系统的控制方程[3]可表示为

V″″(x)+PV″(x)+(K-Λ2)V(x)=0

x∈(0,1)

(1)

相应的边界条件是：

(2)

(3)

2 广义微分求积法

GDQR的基本思想是用某一函数在物理域上的所有离散点上的函数值及其偏导数值的加权和来逼近该函数在某一离散点偏导数，函数ψ(x)在点x=xi处的第r阶导数可近似写成：

(i=1,2,…,N)

(4)

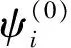
{U}T={U1,U2,…,UK,…,UM}=

文献[6-7]介绍了权系数的获取及网点划分方式，本文采用上述文献中的cos型网点划分方式，即

(i=1,2,…,N)

(i=1,2,…,N)

(5)

{U1,U2,…,Uk,…,UN+2}=

(6)

将以上两式运用到梁系统的控制方程和边界条件，则方程(1-3)可以写成模拟方程：

(K-Λ2)Ui=0

(i=2,3,…,N-1)

(7)

(8)

(9)

用下标b表示边界上的元素,d表示非边界上的元素，则有：

Ub={U1,U2,UN+1,UN+2}T

Ud={U3,U4,…,UN-1,UN}T

(10)

将上述(7-9)三式改写成矩阵形式：

(11)

消除变量Ub，对上式进行整理可得特征徝方程：

S{Ud}=(Λ2-K){Ud}

(12)

[S]=[Sdd]-[Sdb][Sbb]-1[Sbd],矩阵S中包含了KθL、KTL、KθR、KTL、P、η等参量,在四个无量纲弹簧刚度确定的情况下，固定η，K，逐步增大P，可由矩阵S得到相应的特征值Λ，如果P使频率参数为0，则P为分叉失稳载荷；如果使频率参数有两个相等的根，则P为颤振失稳载荷，最小的分叉失稳和颤振失稳载荷就是系统的临界载荷。

3 计算结果

本节首先运用GDQR分析一定弹性地基模量下受剪切力作用一端固定约束、一端支撑弹簧约束梁的临界载荷，通过与文献[3]的结果进行比较，验证了基于GDQR的计算结果的准确性；进而讨论了一端固定约束、一端支承弹簧支承梁，在一定支承弹簧刚度下，弹性地基模量对临界载荷随剪切系数的变化的影响；进一步研究了特定弹性地基模量、不同支承弹簧刚度下，临界载荷随剪切系数的变化规律；接着分析了一端固定约束、一端扭转弹簧支承，不同扭转弹簧刚度下，临界载荷随剪切系数的变化情况；最后探讨了弹性地基模量和弹簧刚度对一端固定约束、一端弹性支承梁的弹性失稳区域的影响。

3.1 GDQR方法验证

为验证基于GDQR的计算结果的正确性，本文采用文献[3]中相应的结果进行比较,在本算例中，采用与文献[3]一致的参数，即K=0,βθL=βTL=∞,βTR=βθR=0，运用GDQR分析受剪切力作用下一端固定约束、一端悬臂梁的稳定性，得到不同剪切系数下的临界载荷值，计算结果如图2所示。

图2 GDQR得到的临界载荷与文献[3]中临界载荷比较Fig.2 The comparision between the critical load calculated by GDQR and the result in Ref[3]

由图2可以看出，两种方法结果吻合的很好，由此说明，基于GDQR方法分析弹性地基上受切向力作用弹性支承梁稳定性问题是准确、有效的。

3.2 弹性地基对临界载荷随剪切系数的变化的影响

图3给出了βθL=βTL=∞,βθR=0,βTR=5，即左端固定约束，右端支承弹簧支承，不同弹性地基模量下，临界载荷随剪切系数的变化曲线，从图中可以看出，梁的颤振失稳临界载荷不随弹性地基模量的改变而变化，另外当弹性地基模量K=25.019时，失稳形式发生转变时的临界载荷不变；而当K>25.019时，失稳形式发生转变时，临界载荷下跳；当K<25.019时，失稳形式发生转变时，临界载荷上跳。本文所取的右端支承弹簧刚度βTR=5，βTR取其它不同值时也有类似的规律。

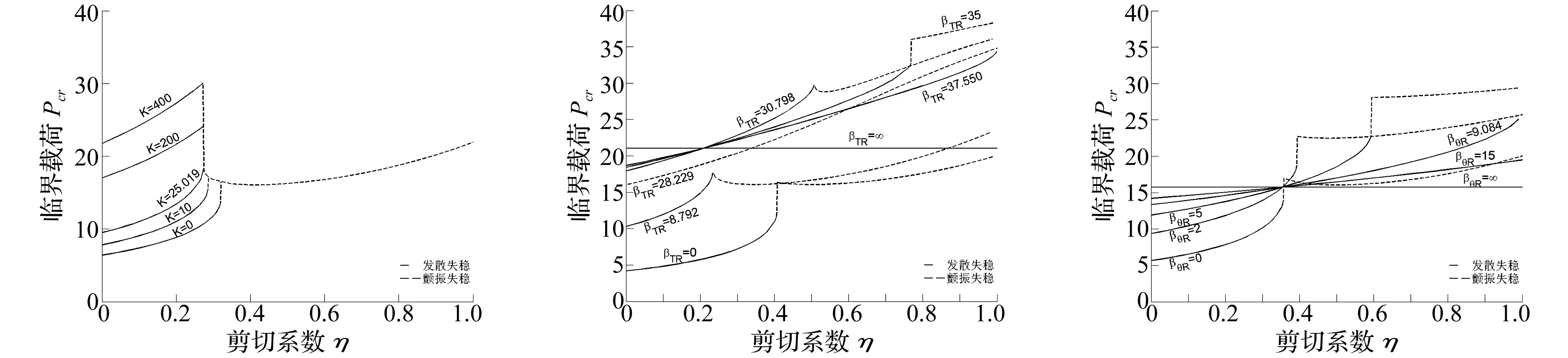
图3 不同Winkler弹性地基模量时，临界载荷随剪切系数的变化曲线Fig．3CriticalloadversustangencycoefficientunderdifferentWinklerelasticfoundationmodulus图4 不同支承弹簧刚度下，一端固定约束，一端支承弹簧支承梁临界载荷随剪切系数的变化曲线Fig．4Criticalloadversustangencycoefficientforaclamped⁃translationalspringsupportedbeamunderdifferenttranslationalspringconstants图5 不同扭转弹簧刚度，一端固定约束，一端扭转弹簧支承梁临界载荷随剪切系数的变化曲线Fig．5Criticalloadversustangencycoefficientforaclampedrotationalspringsupportedbeamunderdifferentrotationalspringconstants

3.3 特定弹性地基下，临界载荷随剪切系数的变化规律

图4给出了K=0,βθL=βTL=∞,βθR=0，即弹性地基模量取10，左端固定约束、右端支承弹簧支承时，不同支承弹簧刚度下，临界载荷随剪切系数的变化曲线，计算发现，当βTR>37.550时,系统的失稳形式是发散失稳,当βTR<37.550时，随着剪切系数的增大，存在一个失稳形式由发散向颤振转换的临界值，失稳形式转换时，临界载荷会有一个有限的跳跃，当30.789<βTR<37.550，βTR<8.792时临界载荷将上跳，而当8.792<βTR<30.798时，临界载荷将下跳，因此，剪切系数增强或降低系统的稳定性取决于无量纲支承弹簧刚度βTR的值。

图5给出K=20,βθL=βTL=∞,βTR=0，即弹性地基模量取20，左端固定约束，右端扭转弹簧约束，不同扭转弹簧刚度时，临界载荷随剪切系数的变化曲线，可以发现，当扭转弹簧刚度取值比较小时，随着剪切系数的增加，同样会存在一个失稳形式发生转变的临界值，此时临界载荷将也会有一个有限的跳跃；而当扭转弹簧刚度取值大于某一值时，梁的失稳形式均转变为发散失稳。

另外，结合图4与图5可以发现，一定弹性地基模量下，当一端固定约束，另一端的支承弹簧刚度或者扭转弹簧刚度取无穷大时，临界载荷的大小不随剪切系数的改变而变化。以上图4与图5所对应两种支承情况中，本文所取的弹性地基模量分别是K=10、K=20，而当K取其它值时，均也会有类似的规律。

3.4 弹性地基和弹簧刚度对弹性失稳区域的影响

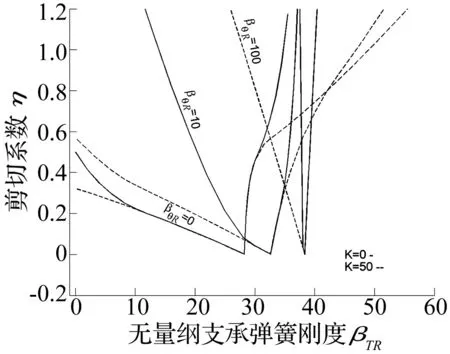
图6 K=0,K=50时，不同βθR下，分散/颤振失稳临界剪切系数随βTR变化曲线Fig.6 Critical tangency coefficient versus translational spring constant of flutter and divergence instability with different value of rotational spring constants and elastic foundation modulus K=0,K=50

图6和图7分别给出了K=0,K=50，一端固定约束、一端弹性约束梁，剪切系数随约束弹簧刚度变化的分散/颤振失稳区域。图中边界线及其以上的区域失稳形式是颤振失稳，其它区域失稳形式是发散失稳，实线对应弹性地基模量K=0的情况，虚线对应K=50的情况。对比发现：当扭转弹簧刚度增加时，颤振失稳区域减小，当支承弹簧刚度增加时，颤振失稳区域增加，而当弹性地基模量增加时，颤振失稳区域会随之增加。

图7 K=0,K=50时，不同βTR下，分散/颤振失稳临界剪切系数随βθR变化曲线Fig.7 Critical tangency coefficient versus rotational spring constant of flutter and divergence instability with different value of translational spring constants and elastic foundation modulus K=0,K=50

4 结 论

本文运用GDQR研究弹性地基上复杂弹性支承条件下受切向力作用梁的稳定性问题，通过计算受剪切力作用下一端固定约束、一端支撑弹簧约束梁的临界载荷，并将计算结果与文献[3]中相应的值进行比较，验证了基于GDQR计算结果的准确性, 进而讨论了弹性地基模量对临界载荷随剪切系数变化的影响，同时分别探讨了特定弹性地基模量下，一端固定约束、另一端支承弹簧支承，不同支承弹簧刚度下和一端固定约束、另一端扭转弹簧约束，不同扭转弹簧刚度下，临界载荷随剪切系数变化的规律；最后研究了弹性地基模量和弹簧刚度对一端固定约束、另一端弹性支承梁弹性失稳区域的影响。

结果表明：弹性地基上的一端固定约束、另一端支承弹簧支承梁，在特定支承弹簧刚度下，梁的颤振失稳临界载荷不受弹性地基模量的影响；而且存在一个临界弹性地基模量，使失稳形式发生改变时的临界载荷不发生变化；当弹性地基模量一定时，剪切系数增强或降低系统的稳定性取决于支承弹簧刚度βTR的值。对于一端固定约束、另一端扭转弹簧约束梁，扭转弹簧刚度βθR决定梁的失稳形式以及临界载荷随剪切系数的变化规律。一端固定约束、另一端弹性支承梁，当支承弹簧刚度或者扭转弹簧刚度取无穷大时，临界载荷的大小将不随剪切系数的改变而变化；其颤振失稳区域会随扭转弹簧刚度的增加而减小，随支承弹簧刚度的增加而增加，随弹性地基模量的增加而增加。

[ 1 ] Smith T E, Herrmann G. Stability of a beam on elastic foundation subjected to a follower force [J]. Journal of applied Mechanics, 1972, 39(2): 628-629.

[ 2 ] Lee S Y, Kuo Y H, Lin F Y. Stability of a Timoshenko beam resting on a Winkler elastic foundation [J]. Journal of Sound and Vibration, 1992, 153(2): 193-202.

[ 3 ] Lee S Y, Liu J C，Hsu K C. Elastic instability of a beam resting on an elastic foundation subjected to a partially tangential force [J]. Computes & Structures, 1996, 59(6): 983-988.

[ 4 ] 马小强, 向宇, 黄玉盈. 求解弹性地基上任意支承输液直管稳定性问题的传递矩阵法[J]. 工程力学, 2004, 21(4): 194-198. MA Xiao-qiang, XIANG Yu, HUANG Yu-ying. A transfer matrix method for solving stability of pipes conveying fluid on elastic foundation with various end supports [J]. Engineering Mechanics, 2004, 21(4): 194-198.

[ 5 ] 包日东, 闻邦椿. 用微分求积法分析不同支承条件下水下输流管道的动力特性与容许悬跨长度[J]. 地震工程与工程振动, 2009, 29(2): 131-137. BAO Ri-dong, WEN Bang-chun. Dynamic characteristics and limited span analysis of submarine pipeline under different supporting conditions [J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(2): 131-137.

[ 6 ] Wu T Y, Liu G R. A Differential Quadrature as a numerical method to solve differential equations [J]. Computational Mechanics, 1999，24 (3), 197-205.

[ 7 ] Wu T Y, Liu G R. The generalized differential quadrature rule for fourth-order differential equations [J]. International Journal for Numerical Methods in Engineering, 2001，50: 1907-1929.

[ 8 ] WANG Lin, NI Qiao. In-plane vibration analyses of curved pipes conveying fluid using the generalized deferential quadrature rule[J]. Computes & Structures,2008,86:133-139.[ 9 ] Marzani A, Tornabene F, Viola E. Nonconservative stability problems via generalized differential quadrature method [J]. Journal of Sound and Vibration, 2008, 315(1-2): 176-196. [10] 李威, 曾志松, 韩旭. GDQR求解切向力下复杂弹性支承梁的稳定性[J]. 华中科技大学学报(自然科学版), 2012, 40(11): 68-71. LI Wei, ZENG Zhi-song, HAN Xu. Stability of elastically supported beams subjected to a partially tangential force based on GDQR [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(11): 68-71.

Stability of a beam on elastic foundation subjected to a tangential force

LI Wei1，ZENG Zhi-song1，HAN Xu2

(1.School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2.College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;3. Hubei Key Laboratory of Naval Architecture & Ocean Engineering, Hydrodynamics (HUST), Wuhan 430074, China)

Generalized differential quadrature rule(GDQR)was applied to investigate the stability of a complexly and elastically supported beam on an elastic foundation subjected to a partially tangential force. Based on the motion equations and boundary conditions of an elastically supported beam, the matrix eigenvalue equation combining the dynamic equations and boundary conditions was derived after the beam was discretized with GDQR. After analyzing the corresponding eigenvalue equations, the effects of elastic foundation modulus, shear coefficient, and complex boundary conditions on the beam critical load were discussed. The influences of elastic foundation modulus and support spring stiffness on the instability area of a clamped-elastically supported beam were studied and some useful conclusions were obtained. It was shown that GDQR is an effective means for solving the stability of such systems.

generalized differential quadrature rule (GDQR); stability; elastic foundation; tangential force

国家杰出青年科学基金项目(10725208)

2012-12-17 修改稿收到日期：2013-05-15

李威 男，副教授，1975年生

O327

A

10.13465/j.cnki.jvs.2014.08.033