基于混合高斯输出贝叶斯信念网络模型的设备退化状态识别与剩余使用寿命预测方法研究

张星辉， 康建设， 赵劲松,2， 肖 雷， 曹端超， 刘 浩

(1.军械工程学院，石家庄 050003；2.军事交通学院，天津 300161；3.重庆大学 重庆 400030)

基于混合高斯输出贝叶斯信念网络模型的设备退化状态识别与剩余使用寿命预测方法研究

张星辉1， 康建设1， 赵劲松1,2， 肖 雷3， 曹端超1， 刘 浩1

(1.军械工程学院，石家庄 050003；2.军事交通学院，天津 300161；3.重庆大学 重庆 400030)

提出了基于混合高斯输出贝叶斯信念网络模型的设备退化状态识别与剩余使用寿命预测新方法，将变量消元和期望最大化算法相结合对模型进行推理，应用聚类评价指标对状态数进行优化，通过计算待识别特征向量的概率值来确定设备当前的退化状态，在退化状态识别的基础上，提出了剩余使用寿命预测方法。最后，分别应用50组轴承全寿命仿真数据和3组轴承全寿命实验数据对模型进行验证。结果表明，该模型可有效地识别设备的退化状态并对剩余使用寿命进行预测。

混合高斯输出贝叶斯信念网络模型；退化状态识别；剩余使用寿命预测；轴承

基于状态的维修(Condition Based Maintenance，CBM)是指由安装在设备外部的传感器获取设备运行时的状态信息后，通过对状态信息进行分析，判断设备当前所处的退化状态并对设备的剩余使用寿命(Remaining Useful Life，RUL)进行预测，在此基础上对设备的维修活动进行规划。目前，RUL预测方法主要有两种：基于物理模型的方法和基于数据驱动的方法。Bechhoefer等[1]应用Paris法则构建了裂纹与振动监测指标之间的关系并对RUL进行预测。Jin等[2]研究了卫星动量轮的故障机理并建立了RUL预测模型。对于复杂设备的部件而言，由于其故障机理非常复杂，很难建立有效的物理模型对RUL进行预测。而基于数据驱动的方法则可以直接利用状态监测数据对RUL进行预测。其主要方法有：人工神经网络(Artificial Neural Network，ANN)[3-4]、隐马尔可夫族模型(Hidden Markov Models，HMM)[5-11]、支持向量机(Support Vector Machine，SVM)[12-15]、比例风险模型(Proportional Hazards Model，PHM)[16-17]和状态空间模型(State Space Model，SSM)[18-20]等。

如果按照退化状态进行分类，基于数据驱动的方法可以分为两类：连续退化状态模型和离散退化状态模型。对于连续退化状态模型，其需要用最新的退化特征对模型参数不断的更新。如果退化特征非平稳且有较大的噪声，那么模型的性能将会下降并导致虚警率升高。而离散退化状态模型则能克服这些不足，对退化特征的平稳性要求较低。与已有的离散退化状态模型(HMM等)相比，贝叶斯信念网络(Bayesian Belief Networks，BBN)模型[21-24]结构更易于扩展，且有较强的退化状态识别能力。孟光磊等[25]构建了混合贝叶斯网络对空域目标的威胁进行评估。王利民等[26]提出了具有抗噪音能力的增量式混合贝叶斯网络。王双成等[27-28]对混合贝叶斯网络结构的学习方法进行了研究。Tobon-Mejia等[11]应用混合高斯输出HMM(Mixture of Gaussian Hidden Markov Model, MoG-HMM)对设备的退化过程建模并对其RUL进行预测。借鉴混合高斯输出HMM的模型结构，可以构建与之有相同功能且结构更为简化的混合高斯输出贝叶斯信念网络(Mixture of Gaussian Bayesian Belief Networks，MoG-BBN)。且实验分析证明MoG-BBN退化状态识别效果要优于MoG-HMM，因此该研究采用MoG-BBN对设备退化过程进行建模。

退化状态识别需要提取退化特征向量，该特征向量可由时域特征、频域特征和时频域特征中的一种或者多种共同组成。本文应用小波包分解提取退化特征向量。目前，如何合理划分设备的退化状态数还需要进行更为深入的研究，它是退化状态识别和RUL预测乃至维修决策的前提。为此，本文应用聚类指标确定退化状态数。然后应用已知退化状态序列的设备历史数据对模型进行训练。模型训练好后即可对新设备的退化状态进行识别并结合预测模型对RUL进行预测。最后，仿真数据和实验数据验证了方法的有效性。

1 MoG-BBN基本原理

图1 贝叶斯信念网络Fig.1 Bayesian Belief Network

BBN是一种概率推理网络，它以图形节点表示随机变量，节点之间的有向箭头表示随机变量之间的因果关系。BBN也是一种在不确定条件下强有力的知识表达和推理方法。BBN中节点所代表随机变量的取值可以是连续的，也可以是离散的。连续变量可以服从任意分布，离散变量的取值可以是两个或多个。本文构建的MoG-BBN模型，其网络结构如图1所示：

MoG-BBN模型参数描述如下：

(1)X表示隐状态，代表设备的退化状态，取值为1,2,…,a；

(2)M表示混合数，代表组成设备某个退化状态的高斯函数的个数，取值范围为1,2,…,b；

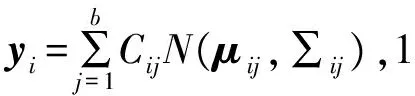
在图1所示的贝叶斯网络中，X是根节点(M和Y的父节点)，M是中间节点(X的子节点，Y的父节点)，Y是叶节点(X和M的子节点)。

该模型和HMM、SVM类似，都是具有模式识别功能的模型。利用已知类别的数据({yi,xi}，i=1,2,…,n)对模型进行训练，再利用该模型对未知类别的数据(yj，j=1,2,…,n)进行分类。在退化状态识别中，X表示设备的退化状态，Y表示经过信号处理得到的反映某时刻设备退化的特征向量，y表示该随机变量的值。识别过程即求取P(X|Y)的过程，其可以通过VE-EM算法实现。

2 VE-EM算法

2.1 变量消元(Variable Elimination，VE)算法

根据贝叶斯信念网链规则得：

(1)

根据条件概率公式得：

(2)

式(2)中P(X,Y=y)可表示为

(3)

式(2)中P(Y=y)可表示为

(4)

结合式(1)、(3)、(4)，式(2)可进一步表示为

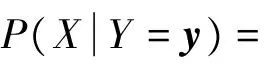
(5)

2.2 期望最大化(ExpectationMaximization，EM)算法

假设训练数据集为{y(1), …,y(n)}，n表示样本数。由式(5)可以最终求得数据集所对应的退化状态序列，因此必须求得P(X)，P(M|X)和P(Y|X,M)，分别对应四个参数：

(1)π：隐状态(设备退化状态)概率分布，πi=P(X=i)，i∈{1, 2, …,a}；

(2)C：隐状态混合系数，Cij=P(M=j|X=i)，i∈{1, 2, …,a}，j∈{1, 2, …,b}；

(3)μ：隐状态产生高斯分布的均值；

(4) ∑：隐状态产生高斯分布的方差。

这四个参数可以表示为：λ=(π,C,μ, ∑)。

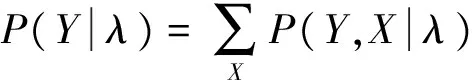
(6)

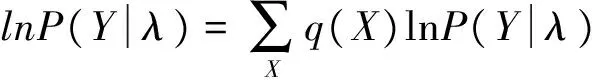
s.t.

(7)

其中，为引入q(X)的未知分布，并给出它的约束条件。根据条件概率公式和贝叶斯公式，(7)式可表示为[29]：

(8)

其中的两项分别为

(9)

(10)

根据Jensen不等式，(10)式可表示为

(11)

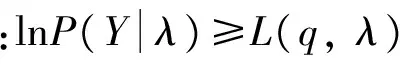
Q(λt,λt-1)+const

(12)

其中：

(13)

(14)

E步：

对所有的(i,j,l)

(15)

i∈{1, 2, …,a}，j∈{1, 2, …,b}，l∈{1, 2, …,n}。

根据贝叶斯公式，式(15)可表示为

(16)

M步：更新参数

(17)

(18)

(19)

(20)

3 基于MoG-BBN的退化识别与RUL预测

设备从正常到失效是一个逐渐退化的过程，即存在“潜在故障—功能故障”间隔。该间隔也称为P-F间隔，如图2所示。“P”点是潜在故障点，是能够发现设备缺陷的点，它通常会以更快的速度退化到功能故障点“F”点。

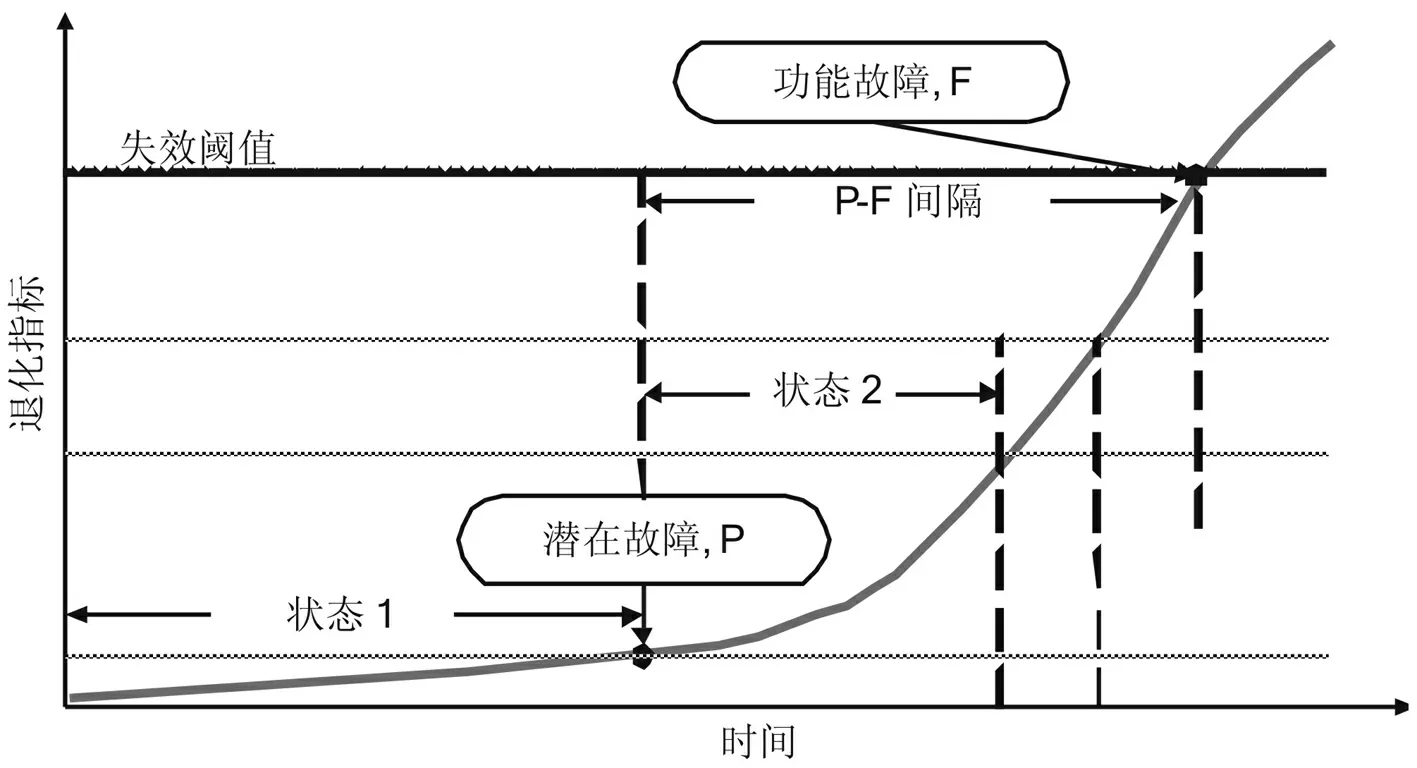
图2 P-F间隔期Fig.2 P-F interval

设备的全寿命过程可分为若干个退化状态，有些退化状态处于潜在故障点“P”之前，退化指标相比于设备刚开始运行时并没有明显的变化。因此，RUL预测不考虑“P”点之前的阶段。对于CBM而言，为确保将设备的停机时间控制到最短，提高设备的可用度，最大化生产效益，需要RUL能够满足维修活动规划(备件订购、运输、维修队实施更换等)。也就是说，只要RUL能够满足这些要求，就说明该预测方法是有效的。

利用MoG-BBN模型对设备退化状态进行识别和RUL预测包括：确定最优退化状态数、状态识别和RUL预测。

3.1 退化状态数优化

设备退化状态数的确定是利用MoG-BBN模型进行退化状态识别和RUL预测的前提。多数研究都是靠经验来确定退化状态数。董明根据油液的污染度将泵轴承分为四个退化状态[7-8]。文献[9]在应用HMM预测时，假设设备的退化状态数为两个(好和坏)。退化状态数的确定大致可分为三种方法：一是由专家根据经验确定；二是利用交叉验证思想以分类器的分类错误率最低来确定；三是应用聚类评价指标确定。专家经验是通过大量实验积累的，对于高可靠、价格昂贵的部件并不适用。利用交叉验证的思想确定最优退化状态数需要对不同的退化状态数都训练分类器并检验其分类错误率，计算时间长，效率低[5]。而应用聚类评价指标确定最优退化状态数则简便易行，计算效率高。因此，本文采用第三种方法。

首先，假设聚类数(退化状态数)为a，a∈{2, 3…,amax}。可任意选择一种模糊聚类方法将提取的特征矩阵分为a类，计算各聚类指标的值，每个聚类数值都有一组评价指标值与其对应，由此可以确定最优的聚类数。聚类评价指标分别为

分割系数[30](Partition Coefficient，PC)，其定义式为

(21)

分割指标[31](Partition Index，SC)，其定义式为

(22)

分离指标[31](Separation Index，SI)，其定义式为

(23)

Xie和Beni指标[32](Xie and Beni’s Index，XB)：其定义式为

(24)

以上表达式中，uil表示第l个样本属于第i类的概率，y(l)表示第l个样本，vi表示第i类的聚类中心，vk表示第k类的聚类中心，1≤i,k≤a，l表示样本数目。对于最优的聚类数目而言，PC取值越大越好，SC、SI和XB取值越小越好。

3.2 基于MoG-BBN的退化状态识别

图3 全寿命过程退化状态识别Fig.3 Degradation state recognition of full life cycle

3.3 基于MoG-BBN的RUL预测

设备全寿命退化过程状态识别结果表示为设备处于每个状态的概率，如图4所示。它表示当设备最开始运行时，其处于正常状态(第一退化状态)的概率为1，然后其概率逐渐下降，到达一定时刻时，第二退化状态的概率逐渐上升，依次往复，当最后一个退化状态的概率为1时，设备失效。这些求取的退化状态概率值是RUL预测的基础。

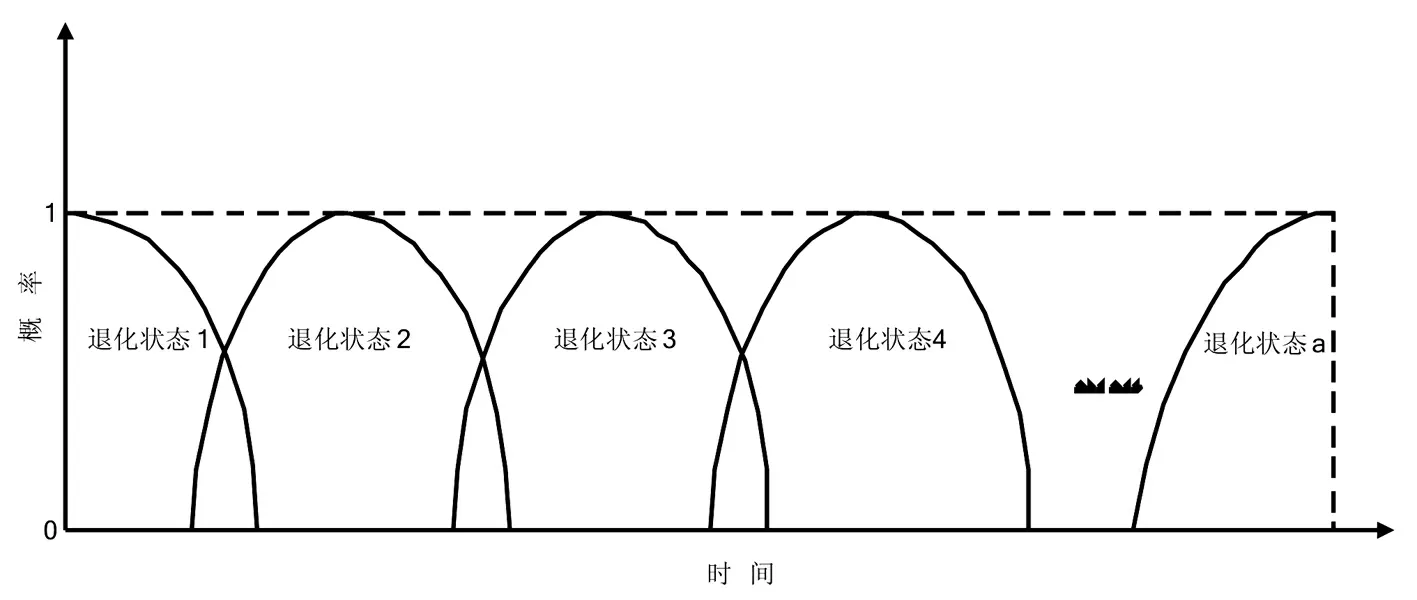
图4 全寿命过程退化状态识别结果示意Fig.4 Degradation state identification results of full life cycle

t时刻设备的RUL可以通过式(25)计算得出：

(25)

其中：

(26)

式中，Dui表示由历史数据得出的设备在第i个退化状态的驻留时间，RULi表示由历史数据得出的设备处于第i个退化状态时的RUL。k为当前状态驻留时间系数，用于调整RUL预测的准确度。

假设设备退化状态的驻留时间服从正态分布，由历史数据可以统计得出各个退化状态驻留时间的均值和方差。最后，根据2Sigma准则得出RUL预测值的范围。待新设备从正常运行到失效后，用所得退化状态识别和RUL预测结果对历史数据进行更新，重新计算各退化状态驻留时间的均值和方差。

基于MoG-BBN的退化状态识别和RUL预测过程可用图5表示。

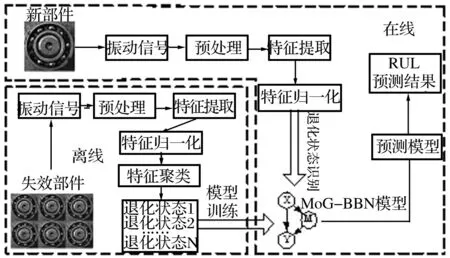
图5 基于MoG-BBN的设备退化状态识别与RUL预测框架Fig.5 Framework of degradation states identification and RUL prediction based on MoG-BBN

4 仿真数据分析

4.1 数据仿真

根据文献[33-34]中的方法对轴承外圈故障进行仿真，所仿真轴承的几何参数为：节径39.039 8 mm、滚动体9个、滚动体直径15.001 2 mm、接触角0°。通过轴承故障特征频率计算公式可求得轴承的频率倍数如表1所示。

表1 轴承各部件故障频率倍数

仿真轴承的转速为1 800 r/min，采样频率为12 kHz，采样持续时间10 s。

图6所示为仿真信号的时域表示，图7为该信号的包络谱。

由于指数函数经常用来描述机械产品的退化规律，可见文献[35-37]。因此，为使得信号的峰值不断增长直至超过预先设定的阈值，可在仿真时，将轴承外圈故障信号乘以一个指数函数。假设轴承的寿命服从威布尔分布，指数函数可由式(27)确定。

eTi/βi=阈值

(27)

Ti表示轴承寿命，βi表示与轴承寿命相对应的参数，当阈值和轴承寿命已知时，可求得βi，从而进行轴承全寿命数据的仿真。取威布尔分布的尺度参数和形状参数为3 500和5，设定峰值20 m/s2为阈值。仿真后，得到50组轴承全寿命数据。图8所示为仿真的前5组轴承全寿命数据的峰值。

图6 轴承外圈故障仿真信号时域表示Fig．6Simulatedsignalofbearingwithanoutracedefect图7 轴承外圈故障仿真信号包络谱Fig．7Frequencyspectrumafterenvelopedemodulation图8 前5组轴承全寿命数据的峰值Fig．8Peakvaluesof5simulatedbearingtest⁃to⁃failuredata

4.2 仿真数据退化状态识别

(1) 状态数优化

用‘db4’小波对轴承仿真数据进行小波包3层分解，提取各频带能量作为特征向量，从而得到每组数据全寿命过程特征矩阵F。对轴承1(第1组数据)的特征矩阵F进行聚类时，取聚类数2～7。分别计算PC、SC、SI、XB的值，结果如表2所示。从表中可以看出，

聚类数目为5时，PC值最大，SC、SI和XB值最小。因此将轴承的全寿命过程分为5个退化状态。应用K均值聚类算法将轴承仿真数据的特征矩阵聚为5类，获得类别序号及聚类中心向量。

为了验证提出的聚类指标确定退化状态数方法的优越性，与交叉验证方法进行对比分析。按照文献[5]中的步骤，可以用交叉验证方法求得轴承1每种退化状态数相对应的分类错误率，如图9所示。

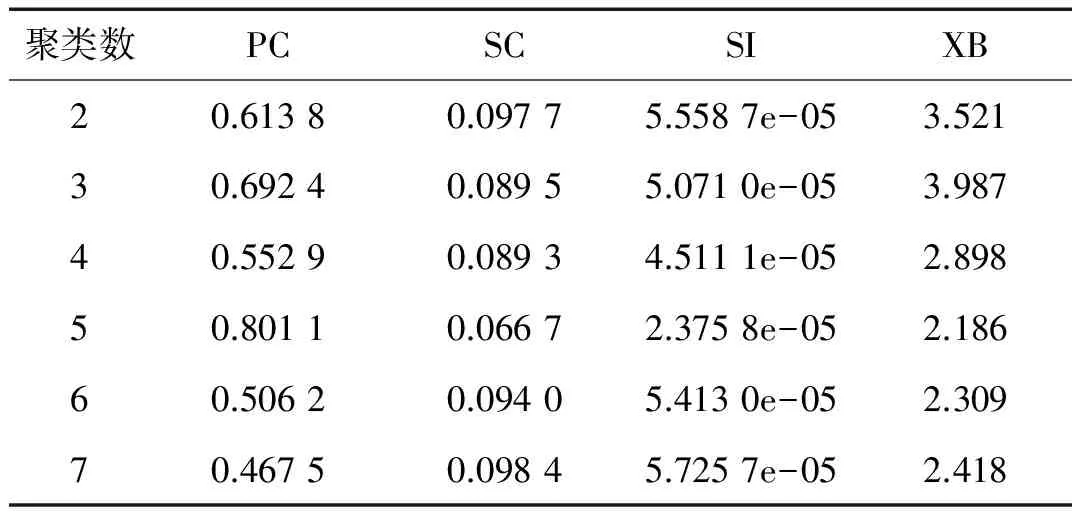
表2 四种聚类评价指标不同状态数目划分取值

图9 轴承退化状态数优化Fig.9 Degradation state number optimization

从图9可以看出，退化状态数为5时，分类错误率最低。和聚类评价指标确定的退化状态数一致。但交叉验证方法确定最优状态数所需的时间为1 113.54 s，而聚类评价指标确定最优状态数仅需13.75 s，大大缩短了计算时间。对于待优化退化状态数范围的选取，一般从2开始，上限则需要根据具体设备的退化过程确定。对于本文中的轴承仿真数据，从其峰值观测，其不可能有太多的退化状态，因此将上限定为7。

(2) MoG-BBN模型训练和退化状态识别

首先，用前40组轴承仿真数据中每个退化状态所对应的特征矩阵训练MoG-BBN模型，应用训练好的模型对第41组轴承仿真数据进行退化状态识别后，该组数据就加入历史数据，重新对MoG-BBN模型进行训练。依次类推，对剩余的9组轴承仿真数据进行状态识别。图10所示为对第41组数据的状态识别结果。

图10所示的结果与图4相似，轴承开始运行时，处于正常状态(第一退化状态)的概率为1， 然后逐渐下降，与此同时，下一退化状态的概率逐渐上升，依次往复，直至轴承失效。

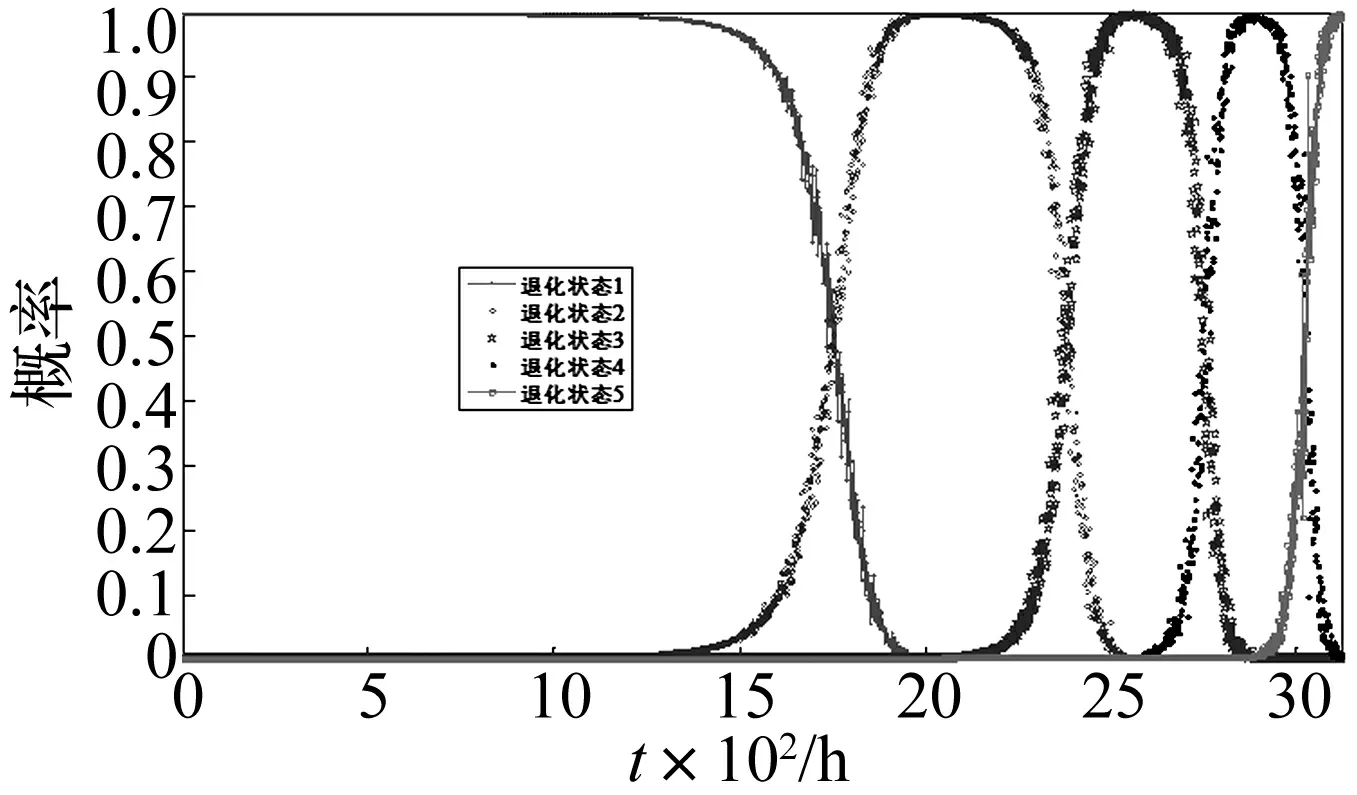
图10 第41组仿真数据的退化状态识别结果Fig.10 State recognition results of 41th bearing simulation data

4.3 仿真数据RUL预测

结合第41组仿真数据退化状态识别的结果，可认为“P”点即是退化状态2起始时刻。因此，对第41-50组仿真组据的RUL预测都是从退化状态2起始时刻开始的。每组数据预测完成后，根据状态识别结果，对退化状态驻留时间的均值和方差重新估计，用于下一组数据的预测。以2Sigma作为RUL预测的范围。预测结果如图11所示。

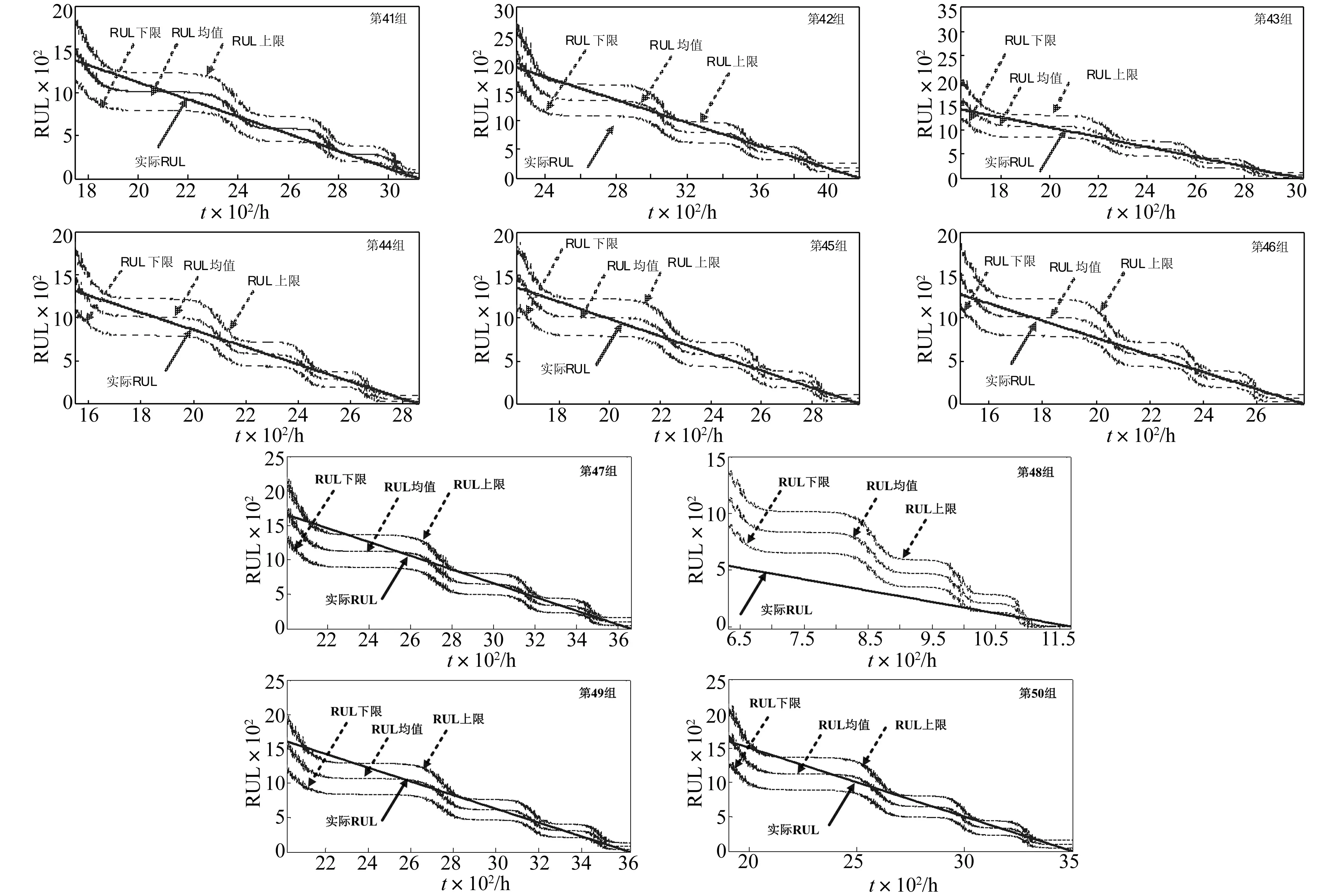
图11 第41～50组轴承全寿命仿真数据RUL预测结果Fig.11 RUL prediction results of the 41st～50th bearing test-to-failure simulation data

从图11中可以看出，对于多数数据而言，其RUL预测结果与实际RUL都较为接近。由于第48组轴承的寿命与平均轴承寿命偏差太大，因此其每个退化状态的驻留时间与平均驻留时间相差也较大。导致预测得到的RUL比实际RUL值小很多，但当轴承将近失效时，预测的RUL与实际RUL值较为接近。像第48组轴承寿命与平均寿命偏差较大的情况属于少数。因此，对于绝大多数轴承而言，该预测方法还是非常有效的。另外在制定维修决策时，充分考虑退化状态识别结果可以避免RUL预测不准确带来的损失。

5 实验数据分析

5.1 预测模型实验验证

轴承全寿命数据来自IMS中心[38]。实验台如图12所示，1个轴上安装了4套Rexnord(莱克斯诺)ZA-2115双列滚子轴承，每列滚子数量为16，滚子组节圆直径为75.501 mm，滚子直径为8.407 4 mm，接触角为15.17°。轴的转速为2 000 r/min，采样频率为20 kHz。每个轴承座都安装2个PCB加速度传感器，分别从水

平和垂直方向采集数据。振动信号由NI公司DAQCard-6062E数据采集卡采集，每次采样长度为20 480个点。轴承2和轴承3额外增加27 210 N载荷。

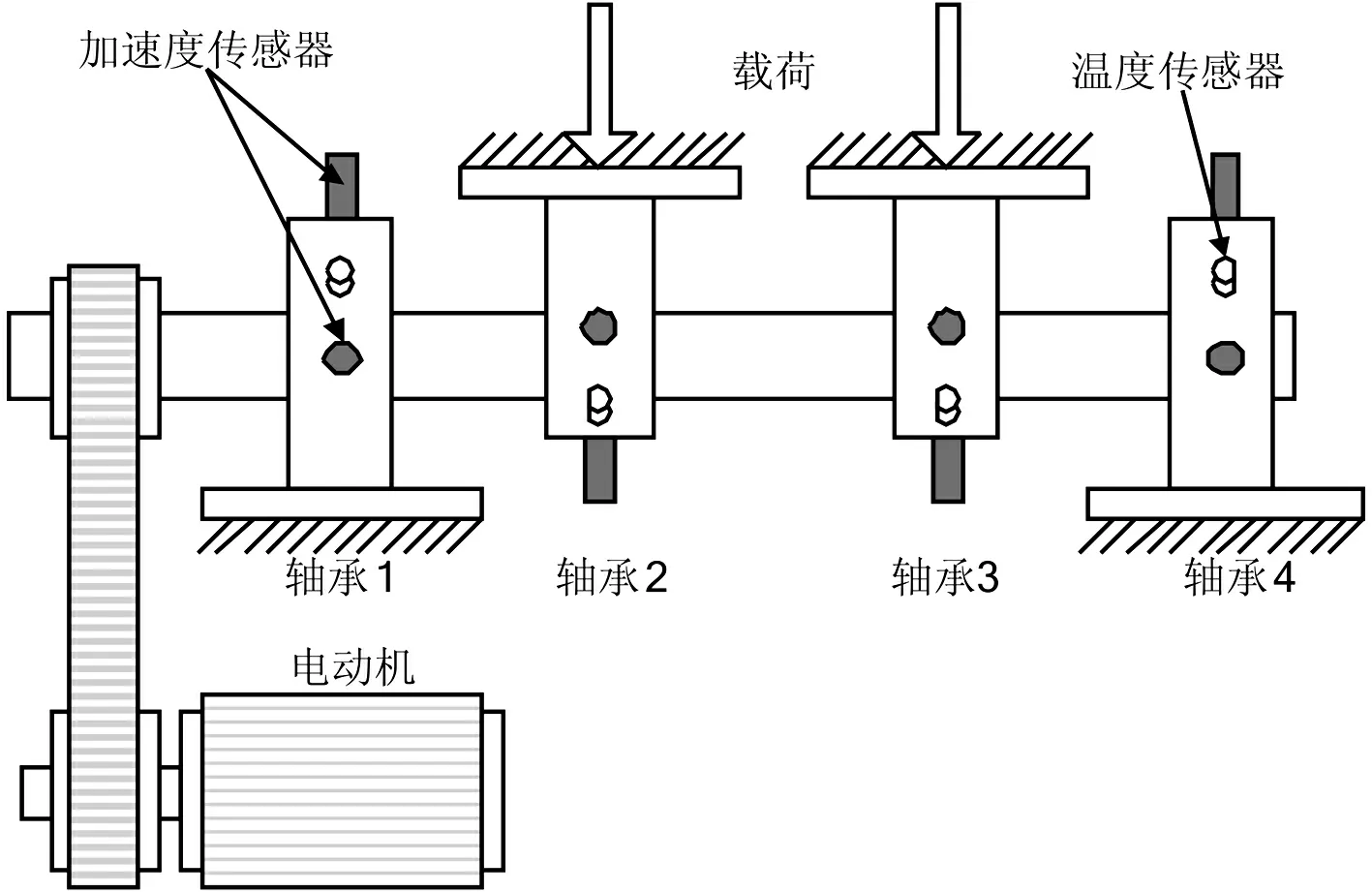
图12 轴承实验台Fig.12 Bearing Test Rig

共进行了3组实验，获得了12个轴承的寿命数据。可以将第一组实验的轴承编号为：轴承1、轴承2、轴承3和轴承4；第二组实验的轴承编号为：轴承5、轴承6、轴承7和轴承8；第三组实验的轴承编号为：轴承9、轴承10、轴承11和轴承12。12组轴承寿命过程的峰值如图13所示。

图13 12组轴承寿命过程的峰值Fig．13Peakvalueoftwelvebearing’slifeprocess图14 轴承4RUL预测Fig．14RULpredictionresultsofbearing4图15 轴承4均方根值Fig．15RootMeanSquarevalueofbearing4

假如设定轴承失效阈值为1.7 m/s2，从图13中可以看出，只有轴承3、轴承4和轴承5的峰值超过了失效阈值。用轴承3和轴承5的数据对MoG-BBN训练，用轴承4的数据对模型进行验证。为了提取有效的轴承退化特征，首先对数据进行包络分析，然后用‘db4’小波对包络信号进行小波包3层分解，以第三层分解系数的能量作为退化特征向量。应用聚类评价指标确定最优退化状态数为3。按照图5所示的流程可以对轴承4的RUL进行预测。结果如图14所示。

对比图14和15可知，应用MoG-BBN模型对轴承4的RUL预测是非常有效的。从时间点1 200/10 min开始，轴承4开始加速退化，其RUL预测值与真实值也开始接近。

5.2 MoG-BBN与MoG-HMM模型对比分析

为了对MoG-BBN和MoG-HMM的退化识别能力进行对比分析，对凯斯西楚大学公开轴承实验数据[39]进行分析。选择驱动端同工况下不同程度的内圈退化数据对模型进行对比，数据的采样频率为12 kHz。轴承型号为6205-2RS JEM SKF，损伤直径分别为0.177 8、0.355 6和0.533 4 mm，分别对应轴承的三种退化状态。工况为1 730 r/min，3马力。将每个退化状态的信号分为24段(每段0.42 s采样)，应用‘db4’小波对信号进行小波包3层分解，以第三层分解系数的能量作为退化特征向量。每个退化状态用4组数据作为训练数据，其它20组数据作为测试数据。对所有的数据的数据进行归一化。MoG-HMM应用PMTK[40]工具箱实现。MoG-HMM和MoG-BBN的初始参数都随机选择。混合数设为2。退化识别结果如图16和17所示。P0.177 8、P0.355 6和P0.533 4分别代表三种退化状态的概率，概率最高的即为识别结果。

图16 MoG-HMM识别结果Fig.16 Degradation state identification using MoG-HMM

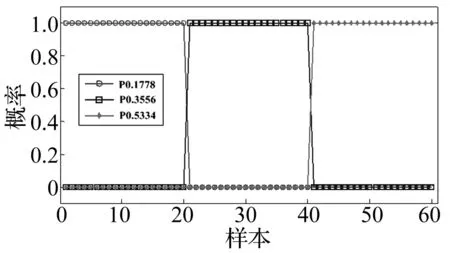
图17 MoG-BBN识别结果Fig.17 Degradation state identification using MoG-BBN

对比分析图14和图15可知，MoG-BBN退化识别效果要优于MoG-HMM。对其它实验数据的分析得到同样的结果。通常，MoG-HMM需要更多的退化特征才能达到较好的效果。而当提取的退化特征有限时，MoG-HMM的识别效果就会较差。与此相的是MoG-BBN即使是在退化特征有限的条件下，仍然能够达到较好的退化识别效果。因此，充分说明了应用MoG-BBN进行退化状态识别和RUL预测的有效性。由于篇幅关系不能和所有的方法一一比较。

6 结 论

(1) 轴承全寿命仿真数据和全寿命实验数据较好地验证了MoG-BBN模型退化状态识别和结合预测模型进行RUL预测的有效性。在具体实施过程中，当前状态驻留时间系数k的选取对RUL预测结果有较大影响。在第41-50组轴承全寿命仿真数据RUL预测中，k的取值分别为0.3、0.9、0.4、0.3、0.3、0.3、0.5、0、0.4、0.5；轴承全寿命实验数据RUL预测中，k的取值为0.7。在下一步研究中，如何选取最优的系数k以提高平均预测准确率是主要研究内容。对于混合数M的选取，目前还没有有效的方法。在下一步的研究中，将以退化识别结果为目标对混合数进行优化。在工程实际中，同一种型号的轴承其失效模式不尽相同，因此其退化过程也不相同，论文中的退化识别和预测方法需要结合实际做进一步的改进。

(2) 基于状态的维修决策优化主要是在RUL预测的基础上对备件订购、运输、库存及维修队派遣等一系列活动进行优化，旨在降低设备停机时间，提高设备的可用度，降低维修费用，最大化生产效益。因此，只要在RUL预测值与实际值相近的时刻，还能留有足够的时间用于维修决策优化活动就说明该方法是有实际意义的。从轴承实验数据研究结果可知，预测值与实际值相近的时间约占全寿命的28%。由文献[41]可知，风电机组的平均故障间隔时间约为10 000～15 000小时。那么，按照MoG-BBN预测的RUL有效时间可以达到2 800～4 200小时，该段时间内能够保障企业有充足时间对各种维修活动进行安排。案例研究发现退化特征的提取对于RUL预测的有效时间(P-F间隔)有重要影响，如果提取的特征能够更早的具有明显的增长趋势(也就是更早地发现“P”点)，那么，RUL的有效预测区间也能更大，就有更加充足的时间对维修活动进行安排。因此，提取更为有效的退化特征是下一步的主要研究内容。

本文提出了基于MoG-BBN模型的设备退化状态识别与RUL预测方法，建立了基于VE-EM的模型推理算法。50组轴承全寿命仿真数据和3组轴承全寿命实验数据较好地验证了论文提出方法的有效性，为设备的健康管理提供了科学依据，对于提高设备的可用度，最大化生产效益具有重要的现实意义。

[ 1 ] Bechhoefer E, Bernhard A, He D. Use of paris law for prediction of component remaining life[C]. IEEE Aerospace Conference, 2008, 1-9.

[ 2 ] Jin G, Matthews D, Fan Y, et al. Physics of failure-based degradation modeling and lifetime prediction of the momentum wheel in a dynamic covariate environment[J]. Engineering Failure Analysis, 2013, 28(3):222-240.

[ 3 ] Gebraeel N, Lawley M, Liu R, et al. Residual life predictions from vibration-based degradation signals: a neural network approach[J]. IEEE Transactions on Industrial Electronics, 2004, 51(3):694-700.

[ 4 ] Tian Z G, Wong L, Safaei N. A neural network approach for remaining useful life prediction utilizing both failure and suspension histories[J]. Mechanical Systems and Signal Processing, 2010, 24(5):1542-1555.

[ 5 ] 滕红智,赵建民,贾希胜,等. 基于CHMM的齿轮箱状态识别研究[J]. 振动与冲击, 2012, 31(5):92-96. TENG Hong-zhi,ZHAO Jian-min, JIA Xi-sheng, et al. Gearbox state recognition based on Continuous Hidden Markov Model[J]. Journal of Vibration and Shock, 2012, 31(5):92-96.

[ 6 ] 胡海峰,安茂春,秦国军,等. 基于隐半Markov模型的故障诊断和故障预测方法研究[J]. 兵工学报,2009,30(1):69-75. HU Hai-feng, AN Mao-chun, QIN Guo-jun，et al. Study on fault diagnosis and prognosis methods based on hidden semi-markov model[J]. Acta Armamentarii, 2009,30(1):69-75.[ 7 ] Dong M, He D. A segmental Hidden Semi-Markov Model (HSMM)-based diagnostics and prognostics framework and methodology[J]. Mechanical Systems and Signal Processing, 2007,21(5):2248-2266.

[ 8 ] Peng Y,Dong M. A prognosis method using age-dependent hidden semi-Markov model for equipment health prediction[J]. Mechanical Systems and Signal Processing, 2011, 25(1):237-252.

[ 9 ] Zhou Z J, Hu C H, Xu D L,et al. A model for real-time failure prognosis based on hidden Markov model and belief rule base[J]. European Journal of Operational Research, 2010, 207(1):269-283.

[10] Baruah P,Chinnam R B. HMMs for diagnostics and prognostics in machining processes[J]. International Journal of Production Research, 2005, 43(6):1275-1293.

[11] Tobon-Mejia D A, Medjaher K, Zerhouni N, et al. A data-driven failure prognostics method based on mixture of gaussians hidden Markov models[J]. IEEE Transactions on Reliability, 2012, 61(2):491-503.

[12] Kim H E, Tan A C C, Mathew J, et al. Bearing fault prognosis based on health state probability estimation[J]. Expert Systems with Applications, 2012,39(5):5200-5213.

[13] Caesarendra W, Widodo A, Thom P H, et al. Combined probability approach and indirect data-driven method for bearing degradation prognostics[J]. IEEE Transactions on Reliability, 2011, 60(1):14-20.

[14] Kang J S, Zhang X H, Zhao J M, et al. Gearbox fault diagnosis based on CHMM and SVM[C]. Proceedings of the 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, 703-708.

[15] Widodo A, Yang B S. Machine health prognostics using survival probability and support vector machine[J]. Expert Systems with Applications, 2011, 38(7):8430-8437.

[16] Carr M J,Wang W. A case comparision of a proportional hazards model and a stochastic filter for condition-based maintenance applications using oil-based condition monitoring information[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2008, 222(1):47-55.

[17] Samrout M, Chatelet E, Kouta R, et al. Optimization of maintenance policy using the proportional hazard model[J]. Reliability Engineering and System Safety, 2009, 94(1):44-52.

[18] Sun J Z, Zuo H F, Wang W B, et al. Application of a state space modeling technique to system prognostics based on a health index for condition-based maintenance[J]. Mechanical Systems and Signal Processing, 2012, 28(4):585-596.

[19] Wang W B. A prognosis model for wear prediction based oil-based monitoring[J]. Journal of the Operational Research Society, 2007, 58(7):887-893.

[20] Wang W B. Overview of a semi-stochastic filtering approach for residual life estimation with applications in condition based maintenance[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2011, 225(2), 185-197.

[21] Xu B G. Intelligent fault inference for rotating flexible rotors using Bayesian belief network[J]. Expert Systems with Applications, 2012,39(1):816-822.

[22] Dey S, Stori J A. A Bayesian network approach to root cause diagnosis of process variations[J]. International Journal of Machine Tools and Manufacture, 2005,45(1):75-91.

[23] Verron S, Li J, Tiplica T. Fault detection and isolation of faults in a multivariate process with Bayesian network[J]. Journal of Process Control, 2010,20(8):902-911.

[24] Sahin F, Yavuz M C, Arnavut Z, et al. Fault diagnosis for airplane engines using Bayesian networks and distributed particle swarm optimization[J]. Parallel Computing, 2007,33(2):124-143.

[25] 孟光磊,龚光红.基于混合贝叶斯网的空域目标威胁评估方法[J].系统工程与电子技术,2010,32(11):2398-2401. MENG Guang-lei, GONG Guang-hong. Threat assessment of aerial targets based on hybrid Bayesian network[J]. Systems Engineering and Electronics, 2010,32(11):2398-2401.

[26] 王利民,苑森淼. 具有抗噪音能力的增量式混合贝叶斯网络[J]. 仪器仪表学报,2005,26(3):221-225. WANG Li-min, YUAN Sen-miao. Incremental hybrid bayesian network with noise resistance ability[J]. Chinese Journal of Scientific Instrument, 2005,26(3):221-225.

[27] 王双成,李小琳,侯彩虹.用于因果分析的混合贝叶斯网络结构学习[J].智能系统学报,2007,2(6):82-89. WANG Shuang-cheng, LI Xiao-lin, HOU Cai-hong. Learning in a hybrid Bayesian network structure for causal analysis[J]. CAAIT Transactions on Intelligent Systems, 2007,2(6):82-89.

[28] 王双成.混合贝叶斯网络隐藏变量学习研究[J]. 计算机学报,2005,28(6):1564-1569. WANG Shuang-cheng. Research on learning the hidden variables of hybrid Bayesian network[J]. Chinese Journal of Computers, 2005,28(6):1564-1569.

[29] Bishop C M. Pattern recognition and machine learning[M]. Springer, 2006:435-455.

[30] Bezdek J C. Pattern recognition with fuzzy objective function algorithms[M]. Plenum Press, 1981.

[31] Bensaid A M, Hall L O, Bezdek J C, et al. Validity-guided (re) clustering with applications to image segmentation[J]. IEEE Transactions on Fuzzy Systems, 1996, 4(2):112-123.

[32] Xie X L, Beni G. A validity measure for fuzzy clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8):841-847.

[33] McFadden P D, Smith J D. Model for the vibration produced by a single point defect in rolling element bearing[J]. Journal of Sound and Vibration, 1984, 96(1):69-82.

[34] Wang Y F, Kootsookos P J. Modelling of low shaft speed bearing faults for condition monitoring[J]. Mechanical System and Signal Processing, 1998, 12(3): 415-426.

[35] Shao Y, Nezu K. Prognosis of remaining bearing life using neural networks[C]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2000: 217-230.

[36] Gebraeel N, Lawley M, Liu R, et al. Residual life predictions from vibration-based degradation signals: A neural network approach[J]. IEEE Transactions on Industrial Electronics, 2004, 51(3):694-700.

[37] Heng A S. Intelligent prognostics of machinery health utilising suspended condition monitoring data[D]. Thesis of Queenland University of Technology, Australia,2009.

[38] NASA Prognostic Data Repository: Bearing Data Set NSF I/UCRC Center for Intelligent Maintenance Systems[DB/OL]. 2010, Available at http://ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-repository.

[39] Bearing Data Center (BDC), Case Western Reserve University Bearing Data[DB/OL]. Available at http://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website,2013.

[40] PMTK: Avaiable at http://code.google.com/p/pmtk3/ (2013).

[41] Tavner P J, Xiang J, Spinato F. Reliability analysis of wind turbines[J]. Wind Energy, 2007, 10(1):1-18.

Equipment degradation state identification and residual life prediction based on MoG-BBN

ZHANG Xing-hui1, KANG Jian-she1, ZHAO Jin-song1,2, XIAO Lei3, CAO Duan-chao1, LIU Hao1

(1.Ordnance Engineering College, Shijiazhuang 050003, China; 2.Military Transportation College, Tianjin 300161, China; 3. Chongqing University, Chongqing 400030, China)

A new approach for equipment health state identification and residual life prediction based on mixture of Gaussian Bayesian belief network (MoG-BBN) was presented. The inference algorithm was established based on variable elimination (VE) and expectation maximization (EM). State number was optimized based on cluster validity indexes. The equipment degradation state was determined through calculating the probability of eigenvectors to be identified. Then, the residual life prediction method was presented based on identifying the degradation state. Finally, 50 bearings whole life simulation data and 3 bearings whole life test data were used to demonstrate the proposed methods. The results showed that the proposed method can be used to identify degradation states of an equipment and predict its residual life effectively.

mixture of Gaussian Bayesian belief network; health state identification; residual life prediction; bearing

国家自然科学基金(51035008);军队“十二五”武器装备预先研究项目(51327020101，51327020304)

2013-02-05 修改稿收到日期：2013-05-17

张星辉 男，博士生，讲师，1984年6月生

TH165.3

A

10.13465/j.cnki.jvs.2014.08.030