超空泡运动体圆柱薄壳动力屈曲及可靠性分析

王杰方， 安伟光， 宋向华

(哈尔滨工程大学 航天工程系, 哈尔滨 150001)

超空泡运动体圆柱薄壳动力屈曲及可靠性分析

王杰方， 安伟光， 宋向华

(哈尔滨工程大学 航天工程系, 哈尔滨 150001)

首先将超空泡运动体模拟成受动态轴向载荷作用的圆柱薄壳，推导了结构的动力稳定性微分方程和动力不稳定区域，然后考虑动态轴向载荷的随机性，采用有限步长迭代法将给出的动力屈曲失稳的多个安全余量方程线性化，并利用逐步搜索法找出有效的安全余量方程，最后结合逐步等效平面法计算了舱段动力屈曲的可靠性指标。通过算例分别分析了载荷频率、速度和载荷比例系数这三个随机参数的变化对动力屈曲可靠性的影响。计算结果为如何选择载荷频率、速度和载荷比例系数的安全范围提供了理论依据。

动力屈曲；可靠性；有限步长迭代法；逐步搜索法；逐步等效平面法

超空泡运动体是在低压汽化或者人工通气形成的超空泡中高速航行的运动体，其头部空化器和水相互接触所产生的阻力随速度的二次方增长，结构所承受的轴向载荷非常大，容易发生屈曲，另外，空泡形状和尺寸的不稳定性会导致载荷随时间变化，对于承受动态轴向载荷作用的圆柱薄壳结构，一般来说，结构只有轴向振动，但是，当轴向载荷的扰动频率与结构横向的固有频率之间的比值存在某种关系时，圆柱薄壳结构的横向振动的振幅迅速增大，导致结构将丧失动力稳定性。因此，研究超空泡运动体的动力屈曲问题是十分必要的。

目前，国内外对超空泡运动体动力屈曲问题的研究主要有：Ruzzene[1]将超空泡运动体模拟成弹性的轴对称壳体，采用Bolotin方法分析了各种轴向屈曲载荷和不同的壳体结构形式下的动态屈曲稳定性；Edward 等[2]用有限元法和多学科优化方法改进了结构的动态进了结构的动态稳定性；施连会等[3]用Bolotin方法对水下航行体的动力稳定性问题进行了数值计算，并分析了载荷参数和航行体变化参数对主动力不稳定区域的影响规律；宋向华等[4]对超空泡射弹的截锥形结构的动力稳定性进行了计算。运动体的静力屈曲可靠性分析的文献主要有：顾永维等[5]将超空泡运动体简化为变截面梁，研究了其抗弯稳定可靠性的问题；周凌等[6]将运动体的环向加肋舱段简化为变厚度的圆柱薄壳，对其进行了屈曲可靠性分析，同时,周凌等[7]对超空泡运动体强度和稳定性两失效模式组成的串联系统进行了非概率可靠性分析。

现有资料中，分析超空泡运动体的动力屈曲和静力屈曲可靠性的文献较多，但是分析动力屈曲可靠性的文献极少，而实际情况下，与载荷相关的几何参数、物理参数、流场参数等都存在随机性，结构的动力不稳定区也存在随机性，因此，在确定性动力屈曲分析的基础上，研究超空泡运动体动力屈曲的可靠性是十分必要的。

文中将有限步长迭代法和逐步等效平面法相结合，将功能函数线性化，并计算结构动力屈曲的可靠度指标。有限步长迭代法对于非线性程度较高的极限状态方程收敛速度快、迭代精度高，而等效平面法能得到体系对应的线性功能函数，有利于进一步结合其他子系统计算总系统的可靠度指标。另外，由于圆柱薄壳的动力不稳定区的数目众多，即动力屈曲的安全余量方程众多，而实际影响结构安全的只是那些离载荷频率较近的不稳定区域，称为有效不稳定区，因此，文中还将给出搜索有效安全余量方程的逐步搜索法。

1 超空泡运动体受力分析及动力稳定性分析

1.1 超空泡运动体圆柱薄壳舱段受力分析

对于超空泡运动体水平向前运动时的动力屈曲分析，其受力可以简化为轴向的均布载荷，即头部阻力和尾部推力，二者大小相等，作用在头部空化器的阻力[8]为

(1)

其中，ρw为流体密度，Ac是空化器的横截面积，Cx是空化器的阻力系数，V是航行体的运动速度。零攻角时，圆盘空化器的阻力系数为

Cx=Cx0(1+σ)

(2)

Cx0=0.5+1.81(φ/360-0.25)-2(φ/360-0.25)2

(3)

(4)

其中，φ为空化器锥角，圆盘空化器的锥角180°，σ为空化数，pc为空泡内压力，p∞为环境压力，其表达式为

p∞=ρwgH+p

(5)

其中，H为航行深度，p为标准大气压。

运动体在高速航行过程中，空泡形状和尺寸的不稳定性会导致轴压幅值p0随时间变化，本文将这一动态的轴向载荷简化为[1]

p(t)=p0+pδ(t)=p0+(1+δcosθt)

(6)

(7)

其中，p0为不随时间变化的部分，pδ(t)为随时间变化的部分，δ为扰动载荷的比例系数，是扰动载荷的幅值与载荷p0的比值，θ为扰动载荷的角频率,dn为圆盘空化器的直径。

1.2 动力稳定性微分方程

根据符拉索夫的弹性壳体理论，适用于细长圆柱薄壳的壳体稳定平衡方程应满足：

(1) 平衡方程中，在圆周切线方向考虑横向剪切力的影响；

(2) 几何方程中，在弯曲变形的几何关系中计入切向位移的影响；

(3) 物理方程中，中面力中计入了弯曲变形的影响，而中面外的力中则计入了中面应变的影响。

联立平衡方程、几何方程和物理方程，并引入函数Φ=Φ(α,β,t)，得到用Φ表示的圆柱薄壳舱段的稳定平衡方程为[9]

(2+1)222Φ-

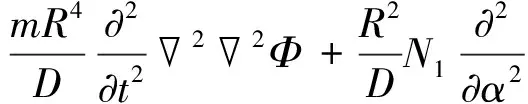
(8)

令Φ(α,β,t)=f(t)sinnαcoskβ(n=iπR/L)(薄壳两端没有径向位移)，i,k取整数值，分别为轴向和周向的半波数，代入式(8)得到圆柱薄壳动力稳定性微分方程为

(9)

其中，

g(n,k)=

从式(9)的量刚分析得，无弯矩状态下的轴向内力N1的量纲应为N/m，即p(t)的量纲为N，文献[3]中p(t)的量纲是N/m2，是错误的。

整理上式得

(10)

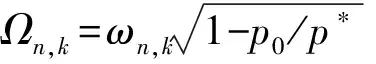
1.3 动力不稳定区

上述方程即mathieu方程，它有一个重要的性质：当它的系数(Ωn,k,γ,θ)存在某些关系时，方程式具有无限增长的解，这些无限增长的解在参数平面上布满了许多区域，即动力不稳定区，根据Bolotin方法，圆柱薄壳的前三阶动力不稳定区域边界为[10]

(11)

(12)

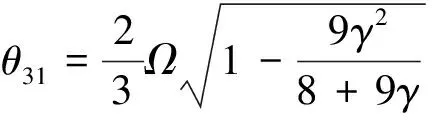
(13)

其中，θ11和θ12，θ21和θ22，θ31和θ32分别为第一、第二和第三阶动力不稳定区域的上边界和下边界。

文献[3]给出了以速度V为变量的动力不稳定区域，是二维的动力不稳定区域，由式(7)可知，其他参数取定值时，p0取决于运动体的航行速度V，而p0决定了mathieu方程中的参数Ωn,k,γ，载荷比例系数δ决定了mathieu方程中的参数γ，因此，下文中给出的以V和δ两者同时作为变量的三维动力不稳定区域能更全面的反映不稳定区的信息。

2 圆柱薄壳动力屈曲可靠性分析

2.1 动力屈曲安全余量方程

当超空泡体动态轴向载荷的频率落入动力不稳定区间时，运动体将发生参数共振。圆柱薄壳动力屈曲可靠性分析即计算动态轴向载荷的频率不落入结构动力不稳定区域的概率。从式(9)和式(11)～(13)可知，每组(i,k)分别对应着三个动力不稳定区域，圆柱薄壳舱段存在多个动力不稳定区域，因此，圆柱薄壳动力屈曲可靠性分析相当于多个安全余量方程的可靠性分析。每组(i,k)对应的第一、二、三阶动力不稳定区域的功能函数形式一致，即

(14)

(15)

(16)

上述三式中，gi(X)<0，则动态轴向载荷的角频率落入了动力不稳定区域；结构发生屈曲失效；gi(X)>0，则结构稳定；gi(X)=0，则结构有周期解，处于失效和可靠的临界状态。

2.2 动力屈曲可靠性分析方法

无论载荷频率落入哪一个动力不稳定区域，结构都会失去稳定性，因此，动力屈曲的可靠性分析等同于多个失效函数串联的可靠性分析。对于串联系统而言，对各失效函数失效概率贡献最大的验算点，对结构体系失效概率的贡献也最大。因此，近似计算串联系统的失效概率时，可利用有限步长迭代法将各失效模式的功能函数在各自的验算点处线性化，并采用等效平面法计算结构的动力屈曲指标。相比一般的迭代法，有限步长迭代法[11]对于非线性程度较高的极限状态方程收敛速度快、迭代精度高，而等效平面法[11]是将那些经过有限步长迭代法线性化后的功能函数逐步等效，最终得到一个线性功能函数，这个线性功能函数中的常数项即为结构的动力屈曲可靠性指标，且这个线性功能函数有利于计算系统的可靠度指标。

对于第i个失效函数，有限步长迭代法在相互独立的正态随机变量空间中的迭代公式为

(17)

(18)

(j=1,2,…,n)

(19)

那么，经有限步长迭代法线性化的功能函数为

其中，

对于串联系统，其失效概率采用逐步等效平面方法计算。逐步等效平面法是通过两两极限状态面的依次等效，逐步减少极限状态面的数目，最后剩下一个极限状态面时，即为系统的功能函数。由式(20)中Ai恒大于0，那么，考虑两个失效函数的情形，其线性化功能函数的等效函数为

(21)

其中，(B11,B12,…,B1n)和(B21,B22,…,B2n)均为单位向量。

两两等效平面对应的可靠指标公式为

βe=βp=-Φ-1[Φ(-β1)+

Φ(-β2)-Φ2(-β1,-β2;ρ12)]

(22)

其中，Φ2(-β1,-β2;ρ12)计算方法[9]如下:

(23)

(24)

B1=-A1(-β1+A1)

(25)

(26)

等效后各随机变量对可靠度指标的敏感系数为

(27)

将敏感系数归一化

(28)

两个失效模式的等效线性功能函数为

(29)

2.3 逐步搜索法

有效不稳定区域是指对动力屈曲可靠性指标有主要影响的那些不稳定区域，从2.1节可知，圆柱薄壳舱段存在多个动力不稳定区域，精确计算超空泡运动体圆柱薄壳舱段的动力屈曲可靠度的过程应为：对每组(i,k)取值所对应的前三阶动力不稳定区域都给出其安全余量方程，再线性化这些安全余量方程，最后利用逐步等效平面法来计算动力屈曲可靠度。显然，对于那些远离载荷频率θ的动力不稳定区域，其可靠性指标很大，当某一不稳定区的可靠性指标β≥βc(βc为有效可靠性指标)时，可以认为这一不稳定区对系统的动力屈曲可靠性指标的影响极小，分析它对系统可靠度的影响是完全不必要的。

本文给出如图1所示的逐步搜索法的计算框图，来筛选有效不稳定区域。图1中，取轴向最大半波数为a，周向最大半波数为b，搜索出a×b组振型对应的3×a×b个不稳定区中，影响动力屈曲可靠性指标的有效不稳定区域。图1中，计算B1j,β1,B2j,β2,B3j,β3，采用式(17)～(20)的有效步长迭代法。搜索出有效的不稳定区域后，采用式(21)～(29)计算圆柱薄壳的动力屈曲可靠性指标即可。

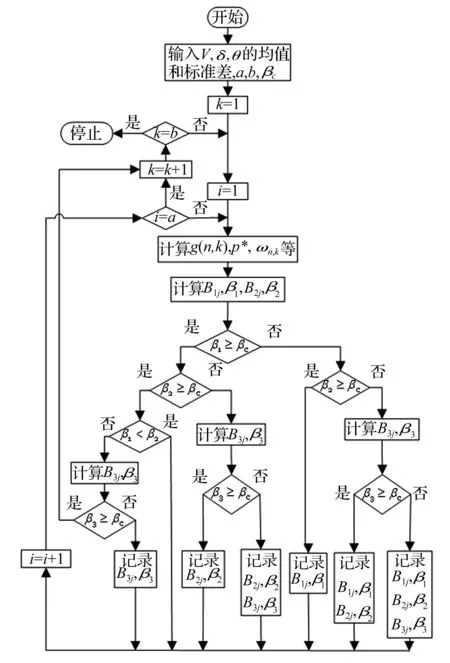
图1 逐步搜索法Fig.1 Step by step searching method

3 超空泡运动体圆柱薄壳舱段数值算例

超空泡运动体航行深度H=10 m，流场密度ρw=1 000 kg/m3，对于自然超空泡，空泡内的饱和蒸汽压pc=2 350 Pa(20℃)，标准大气压p=101 325 Pa。圆柱薄壳舱段的几何参数：R=0.2 m，L=4 m，h=3 mm，dn=0.2 m。材料物理参数：E=209 GPa，ρ=7 850 kg/m3，μ=0.3。

3.1 动力屈曲计算结果及分析

由1.2节可知，i=0时，p*→∞，γ→0，即载荷比例系数δ→0，相当于受静力载荷作用，不必进行动力屈曲及可靠性分析；计算表明，k=0时，f=θ/2π的最低值都在以上2 500 Hz，因此也不必进行动力屈曲及可靠性分析。

图2(a)给出了i=1,k=1时，依赖于V、δ和f=θ/2π这三个参数的前三阶动力不稳定区域；图2(b)给出了i=1,k=1时，前三阶不稳定区域宽度变化图。

图2(a) i=1,k=1时动力不稳定区域Fig.2(a) Dynamic unstable regions(i=1,k=1)

图2(b) i=1,k=1时动力不稳定区域宽度Fig.2(b) The width of dynamic unstable regions(i=1,k=1)

结论1(由图2得到)：

速度和载荷比例系数增大，不稳定的载荷频率值减小，且第一阶不稳定载荷频率减小的速度明显大于后两阶；第一阶动力不稳定区域宽度明显大于后两阶的宽度。因此，对于承受动态轴向载荷且高速运动的超空泡运动体而言，必须充分考虑第一阶不稳定区域对于结构的动力稳定性的影响，避免发生参数共振。

图3给出i=2,k=1时，依赖V、δ和f=θ/2π这三个参数的前三阶动力不稳定区域；图4给出i=3,k=1时的前三阶动力不稳定区域。

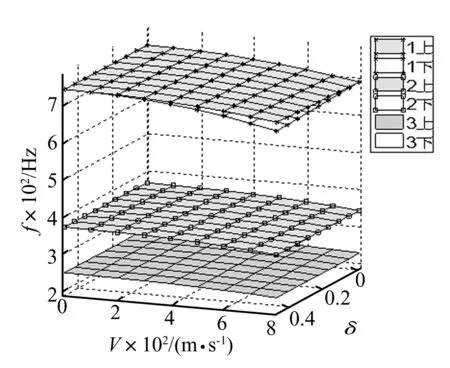
图3 i=2,k=1时动力不稳定区域Fig.3 Dynamic unstable regions(i=2,k=1)

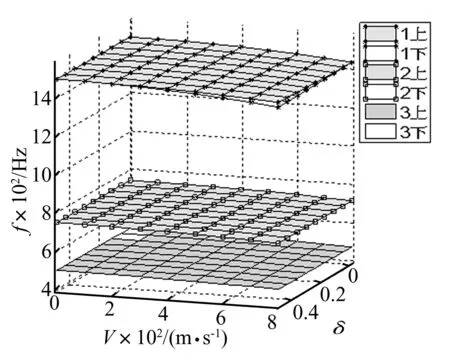
图4 i=3,k=1时动力不稳定区域Fig.4 Dynamic unstable regions(i=3,k=1)

结论2(由图2(a)、图3、图4得到)：

若周向半波数k不变，轴向半波数i增大时，圆柱薄壳舱段的前三阶不稳定区整体上移，且不稳定区域的宽度逐渐减小，进一步计算k取2或3或更大的数值，且i增大时也能得到相同的结论，只是前三节动力不稳定区整体上移的幅度比k=1时要小；但是，若取轴向半波数i不变，周向半波数k增大时，并不能得到以上结论。因此，在图1的逐步搜索法中，以周向半波数k作为外循环，轴向半波数i作为内循环是合理的。

3.2 动力屈曲可靠性计算结果及分析

经过试算，高阶振型对应的动力不稳定区域不仅频率值较高而且宽度较小，实际结构在运动过程中，其载荷的频率值达不到那么高，这些不稳定区域对结构的动力稳定性影响很小，可以忽略。计算表明，图1的逐步搜索法中，取a=5，b=5，βc=5.0是合理的。以f、V和δ作为基本随机变量进行动力屈曲可靠性分析，考虑这三个随机变量相互独立且服从正态分布，它们的随机参数见表1。

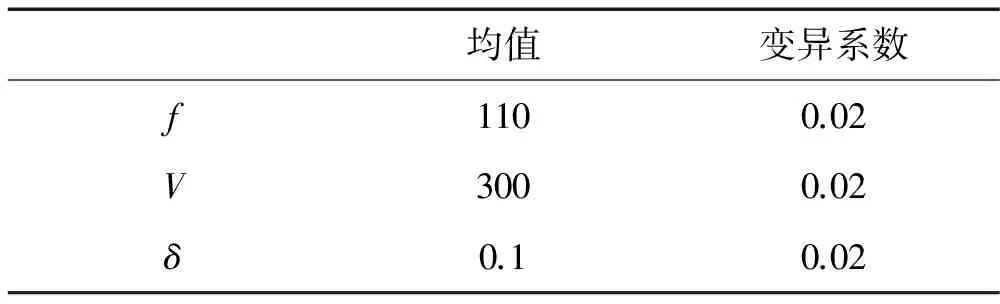
表1 随机变量取值

输入表1中的数据，采用图1所示的逐步搜索法，搜索得到的有效的不稳定区域数目为1，圆柱薄舱段的动力屈曲可靠度指标β=3.266 1。

为了研究三个随机变量的变异程度对动力屈曲可靠性指标的影响，现以表1中随机参数为基准，设为X0，各随机参数的均值不变，将要研究的随机变量的变异系数取0.75X0-2.0X0，其余随机变量的变异系数仍为X0，得到如表2所示的动力屈曲可靠性指标随各随机参数变异系数的变化值，“( )”中的数字为采用逐步搜索法得到的有效不稳定区域的个数。

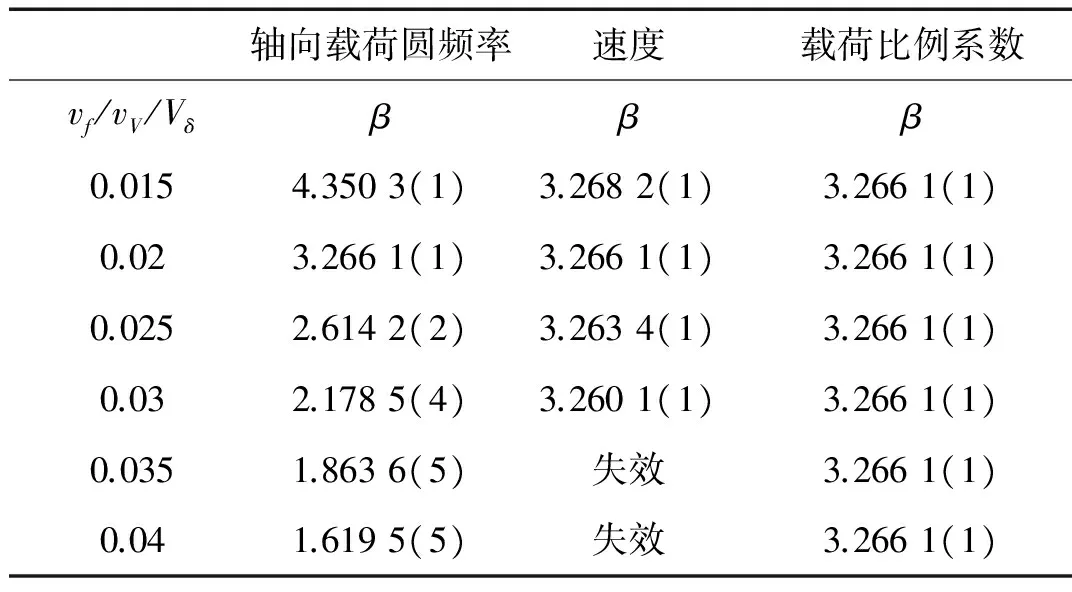
表2 动力屈曲可靠性指标随变异系数的变化值

结论3(由表2得到)：

① 载荷比例系数的变异系数对动力屈曲可靠性指标的影响极小，可以忽略；

② 轴向载荷圆频率的变异系数越大，动力屈曲可靠性指标越小；

③ 速度的变异系数越大，动力屈曲可靠性指标越小。

为了研究三个随机变量的均值对动力屈曲可靠性指标的影响，现以表1中随机参数为基准，设为Y0，各随机参数的变异系数不变，将要研究的随机变量的均值取表3中所示的值，其余随机变量的均值仍为Y0，得到如表3所示的动力屈曲可靠性指标随各随机参数均值的变化值，“()”中的数字为采用逐步搜索法得到的有效不稳定区域的个数。

表3 动力屈曲可靠性指标随均值的变化值

结论4(由表3得到)：

① 载荷比例系数的均值对动力屈曲可靠性指标的影响极小，可以忽略；

② 轴向载荷圆频率的均值位于110 Hz,150 Hz附近时，动力屈曲可靠性指标相对较大，而位于100 Hz,130 Hz附近时，动力屈曲可靠性指标相对较小，这说明轴向载荷圆频率取某些范围内的值时，结构动力屈曲可靠性指标相对较大，结构较安全，且这些范围并不连续。

③ 速度的均值小于400 m/s时，动力屈曲可靠性指标较大，结构相对较为安全，而速度的均值大于450 m/s时，结构会失效，因此，速度取某些范围内的值时，结构较为安全。

4 结 论

从超空泡运动体的动力屈曲分析及可靠性分析的算例得出如下结论：

(1) 速度和载荷比例系数增大，不稳定的载荷频率值减小，且第一阶不稳定载荷频率减小的速度明显大于后两阶；

(2) 周向半波数不变，轴向半波数增大，圆柱薄壳舱段的前三阶不稳定区整体上移，且不稳定区域的宽度逐渐减小；

(3) 速度和轴向载荷圆频率的变异系数越大，动力屈曲可靠性指标越小，载荷比例系数的变异系数对动力屈曲可靠性指标的影响极小，可以忽略；

(4) 载荷比例系数的均值对动力屈曲可靠性指标的影响很小，可以忽略，轴向载荷圆频率和速度的均值取某些范围内的值时，结构动力屈曲可靠性指标相对较大，结构较安全。

综上所述，本文的研究为如何选择载荷频率、速度和载荷比例系数的安全范围提供了理论依据。还有利于计算总系统的可靠度指标。

[ 1 ] Ruzzene M. Dynamic buckling of periodically stiffened shells: application to supercavitating vehicles [J].International Journal of Solids and Structures.2004,41(3-4): 1039-1059.

[ 2 ] Edward A, Vipperla V，Ramana G，et al. Structural response and optimization of a supercavitating torpedo [J].Finite Elements in Analysis and Design.2005,41(6):563-582.

[ 3 ] 施连会，王安稳. 轴向载荷下超空泡航行体动力稳定性的数值研究[J]. 振动与冲击，2011，30(2)：55-59. SHI Lian-hui, WANG An-wen.Numerical study on dynamic stability of supercavitating vehicles subjected to axial loads [J]. Journal of Vibration and Shock, 2011, 30(2): 55-59.

[ 4 ] 宋向华，安伟光，刘明. 轴向周期载荷下超空泡射弹的动力稳定性分析[J]. 哈尔滨工程大学学报，2012，33(10)：1238-1243. SONG Xiang-hua，AN Wei-guang，LIU Ming. Dynamic stability analysis of supercavitating projectile subjected to axial periodic load [J]. Journal of Harbin Engineering University, 2012,33(10):1238-1243.

[ 5 ] 顾永维，安伟光，安海. 水下高速运动体的抗弯稳定可靠性分析[J]. 哈尔滨工程大学学报，2008，29(7)：683-686. GU Yong-wei, AN Wei-guang,AN Hai. Analyzing of buckling resistance of an underwater elasticbody experiencing high speed motion [J]. Journal of Harbin Engineering University, 2008, 29(7): 5683-686.

[ 6 ] 周凌，安伟光，安海. 水下通气超空泡航行体结构屈曲可靠性分析[J]. 工程力学，2010，27(9)：248-256. ZHOU Ling, AN Wei-guang,AN Hai.Structural buckling reliability analysis of underwater ventilated supercavitating vehicles [J]. Engineering Mechanics, 2010, 29(7): 248-256.

[ 7 ] 周凌，安伟光，安海．超空泡运动体强度与稳定性的非概率可靠性分析[J]. 哈尔滨工程大学学报,2009,30(4):362-367. ZHOU Ling，AN Wei-guang，AN Hai．Non-probabilistic reliability analysis of supercavitating vehicles based on structure strength and buckling[J]．Jouranl of Harbin Engineering University,2009,30(4):362-367．

[ 8 ] Ahn S S， Ruzzene M. Optimal design of cylindrical shells for enhanced buckling stability：Application to supercavitating underwater vehicles[J]. Finite Elements in Analysis and Design,2006,42(11):967-976.

[ 9 ] 符拉索夫 瓦 札.壳体的一般理论[M].北京：人民教育出版社，1960:262-271.

[10] 符华,鲍洛金.弹性体系的动力稳定性[M].北京：高等教育出版社,1960:26-31.

[11] 贡金鑫. 工程结构可靠度计算方法[M].大连：大连理工大学出版社,2003:263-268.

Dynamic buckling and reliability analysis of a cylindrical thin shell for supercavitating vehicles

WANG Jie-fang, AN Wei-guang, SONG Xiang-hua

(Department of Aerospace Engineering, Harbin Engineering University, Harbin 150001, China)

Firstly, a supercavitating vehicle was modeled as a cylindrical thin shell loaded with a axial dynamic load. The dynamic stability differential equations and the unstable regions of the shell were deduced. Secondly, the safety margin equations for its dynamic buckling were given and linearized with the limited step length iteration method considering the randomness of axial load. Then, the step-by-step searching method was proposed to search those effective safety margin equations. Finally, the reliability index of the dynamic buckling was calculated with the step-by-step equivalent plane method. Through numerical examples, the influences of change of load frequency, velocity and proportional coefficient of load on the dynamic buckling reliability were analyzed, respectively. The calculation results provided a theoretical basis for choosing the safety range of load frequency, velocity and proportional coefficient of load.

dynamic buckling; reliability; limited step length iteration method; step-by-step searching method; step-by-step equivalent plane method

国家科技部国际合作专项(2012DFR00070)

2013-01-28 修改稿收到日期：2013-05-22

王杰方 女，博士，1987年生

O342

A

10.13465/j.cnki.jvs.2014.08.005