具有不同诱导槽结构的薄壁圆管抗撞性优化

谭丽辉, 谭洪武, 毛志强, 崔晓梅 , 徐 涛

(1. 吉林大学 机械科学与工程学院，长春 130022; 2. 吉林化工学院 机电工程学院，吉林 吉林 132022;3. 中油吉林石化公司有机合成厂，吉林 吉林 132022;4. 中油吉林石化公司炼油厂，吉林 吉林 132022)

具有不同诱导槽结构的薄壁圆管抗撞性优化

谭丽辉1,2, 谭洪武3, 毛志强4, 崔晓梅1,2, 徐 涛1

(1. 吉林大学 机械科学与工程学院，长春 130022; 2. 吉林化工学院 机电工程学院，吉林 吉林 132022;3. 中油吉林石化公司有机合成厂，吉林 吉林 132022;4. 中油吉林石化公司炼油厂，吉林 吉林 132022)

在金属薄壁圆管(原模型)的基础上，分别引入不同形式的圆弧形诱导槽结构并以其为研究对象，建立以诱导槽半径、槽端距、槽间距为优化参数, 以比吸能和最大峰值碰撞力为评价指标的多目标优化模型。分析研究了诱导凹槽、凸槽及凸凹交替的诱导槽结构对薄壁构件吸能、最大峰值碰撞力的影响。采用有限元软件LS-DYNA得到不同几何参数模型的碰撞响应，结合径向基函数法构造近似函数，并采用理想点法进行优化设计，得出使结构最优时的不同形式的诱导槽半径、槽端距及槽间距，从而得到了不同形式的理想诱导槽优化结构。

薄壁构件；比吸能；最大峰值碰撞力；抗撞性；诱导槽

薄壁构件由于重量轻、成本低及其在碰撞过程中的稳定性，而在汽车、轮船、飞机、火车等各类交通工具中作为一种性能良好的缓冲吸能元件得到广泛的应用。薄壁构件作为受撞时主要的承载和吸能元件[1]，在耐撞性设计中要考虑两个约束条件，首先薄壁构件应能够以稳定可控的变形方式吸收尽可能多的能量；其次最大限度的降低碰撞过程中薄壁构件所承受的冲击载荷，较高的冲击载荷会使交通工具产生较大的加速度，从而使乘员受到严重的伤害，故最大冲击载荷应尽可能的小[2]。

为了满足在碰撞过程中薄壁构件吸能的同时尽量降低最大冲击载荷，应对薄壁构件的截面形状、几何尺寸等参数进行科学设计及优化。国内外学者进行了大量的研究，证明圆形截面薄壁构件吸能性优于其它截面，Shakeri等[3]在薄壁圆管上端分别设置了加强环和凹槽两种诱导结构，研究表明改进结构可降低最大冲击载荷，Cho等[4]采用数值方法对具有孔洞型诱导结构的前梁装置进行了抗撞性模拟研究，证明了设定合理的诱导结构在不影响吸能的情况下同时能够降低冲击载荷；张涛等[5]研究了薄壁组合结构及其设计缺陷结构的吸能特性，提出设置一定的诱导缺陷可以降低碰撞过程中的峰值载荷。

目前的多数研究往往局限于在薄壁构件上只设置一种形式的诱导槽结构。如何合理地设置诱导槽，如槽的形状、位置、几何尺寸等都将直接影响薄壁构件的抗撞性。本文从实际出发，在圆形截面薄壁构件上分别设置圆弧形诱导凹槽、凸槽和凸凹交替的诱导槽，研究其对抗撞性的影响。采用非线性有限元软件LS-DYNA得到不同几何参数模型的碰撞响应，以比吸能和最大峰值碰撞力为优化设计指标，诱导槽半径、槽端距和槽间距为动态变量，创建一种多目标优化设计方案，并结合径向基函数法构造优化目标的近似函数，采用理想点法对此多目标优化问题寻优。

1 问题描述

受轴向冲击的薄壁金属圆管在压缩过程中由于褶皱的形成，引起构件连续的塑性压溃。在压溃过程中产生冲击载荷的典型特征参数定义如下。

(1) 最大峰值碰撞力Fmax：在压溃过程中沿轴向产生的冲击载荷的最大值[6]。最大峰值碰撞力会引起较高的加速度，是碰撞过程中需要考虑的重要参数。为了减少对乘员的伤害，故希望在整个压溃过程中最大峰值碰撞力尽可能的小。

(2) 比吸能SEA：单位质量的薄壁构件所吸收的能量[7]。

(1)

式中：Etotal为薄壁构件所吸收的总能量，W为薄壁构件的总质量。为了提高结构的抗撞性，同时满足轻量化的设计要求，应使薄壁构件的比吸能最大化。

比吸能和最大峰值碰撞力在设计上是互相矛盾的，最大峰值碰撞力的降低经常导致比吸能的减少，故需以比吸能和最大峰值碰撞力为优化设计指标。在优化设计过程中，有3个设计参数即诱导槽半径r、槽端距h1和槽间距h2，它们在一定范围内变化。该多目标优化问题可表示为

(2)

事实上，目标函数很难用数学方法精确的表达，本文采用径向基函数模型构造其近似表达式，并采用理想点法寻找多目标问题最优解。

2 结构抗撞性设计

2.1 数值分析

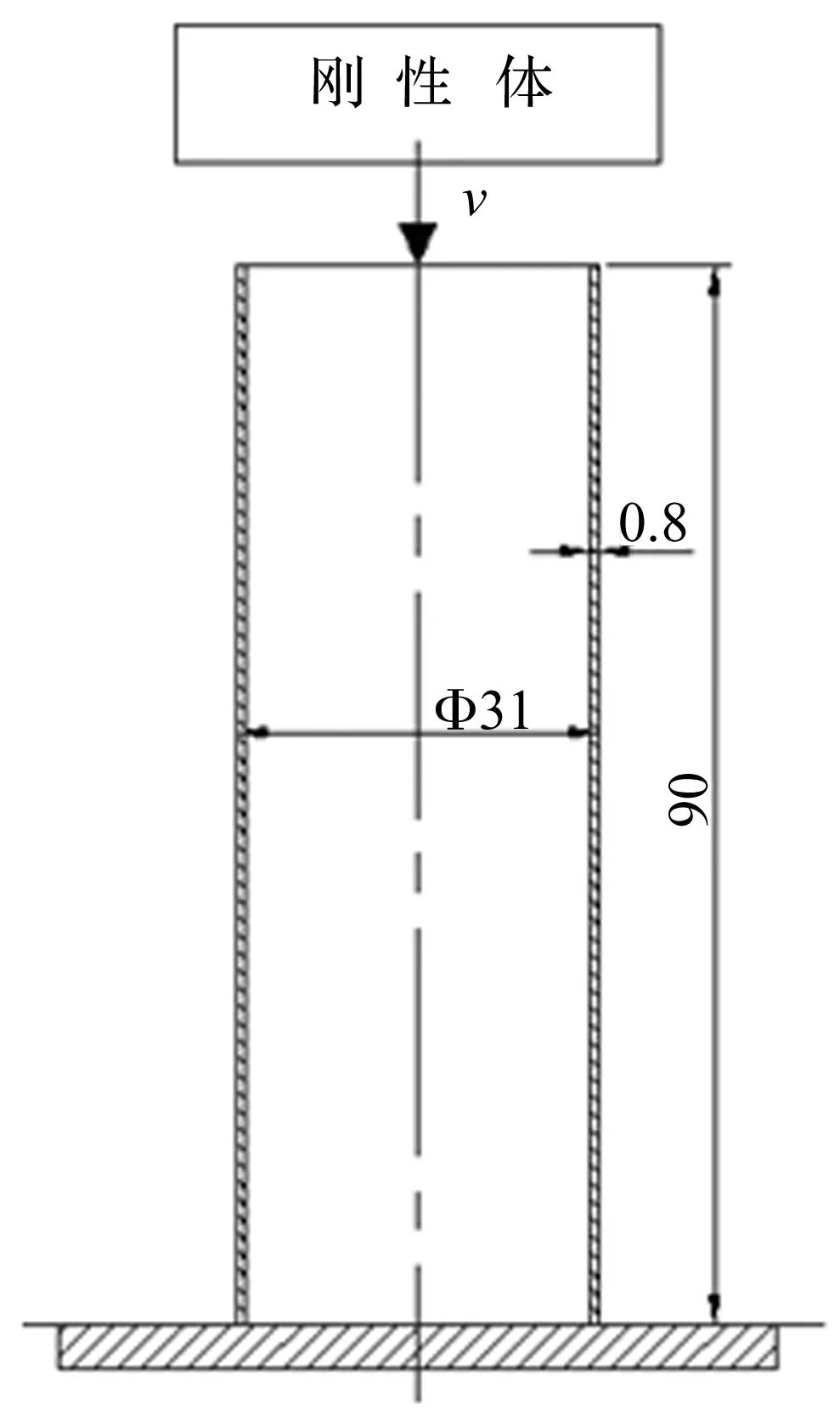
图1 薄壁圆管的分析模型Fig.1 Analysis model of the thin-walled cylinder

为了验证本文有限元分析的精确性，将本文通过有限元分析得到的结果与其它文献中的实验值进行比较。本文采用文献[8]中的数据，首先对薄壁金属圆管(以下称原模型)进行数值分析。如图1所示，圆管下端固定，上端自由并受质量为25 kg,速度为v=15.49 m/s的刚性体冲击作用；圆管厚度t=0.8 mm，长度L=90 mm，直径d=31 mm。

薄壁构件的材料选为高强度钢，密度ρ=7.82×103kg/m3，弹性模量E=207.2 GPa, 泊松比v=0.3，屈服应力σ0=446 MPa。高强度钢材料的动态变形受材料应变率的影响较大，需要在材料模型中考虑应变率的影响。一般采用Cowper-Symonds塑性材料模型[8]

σy=σ0(1+ε/c)1/p

(3)

式中：σy为考虑应变率之后的动态屈服应力，σ0为静态屈服应力；ε为应变率，c和p为该模型中与应变率相关的参数，分别为c=40/s、p=5，应力—应变变化曲线如图2所示。

表1给出了薄壁构件原模型由LS-DYNA计算得到的最大峰值碰撞力、总吸能值、最大压溃位移及其与文献中对应的实验值。通过对比可以看出有限元结果和实验值之间的相对误差很小，可见数值模拟的结果与实验值能够较好地吻合。

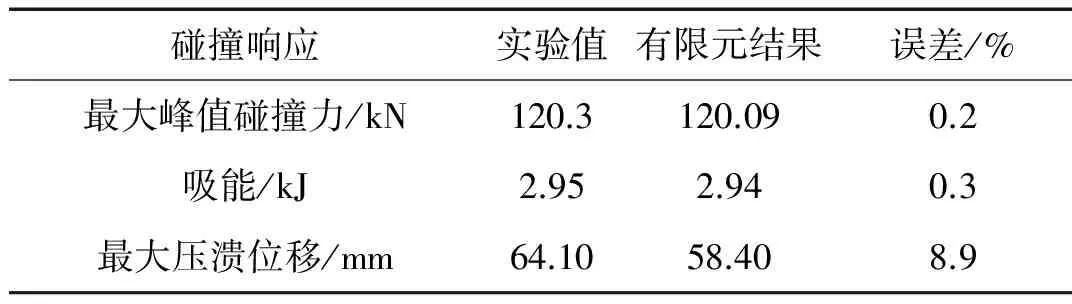
表1 原模型有限元分析结果与实验[8]对比

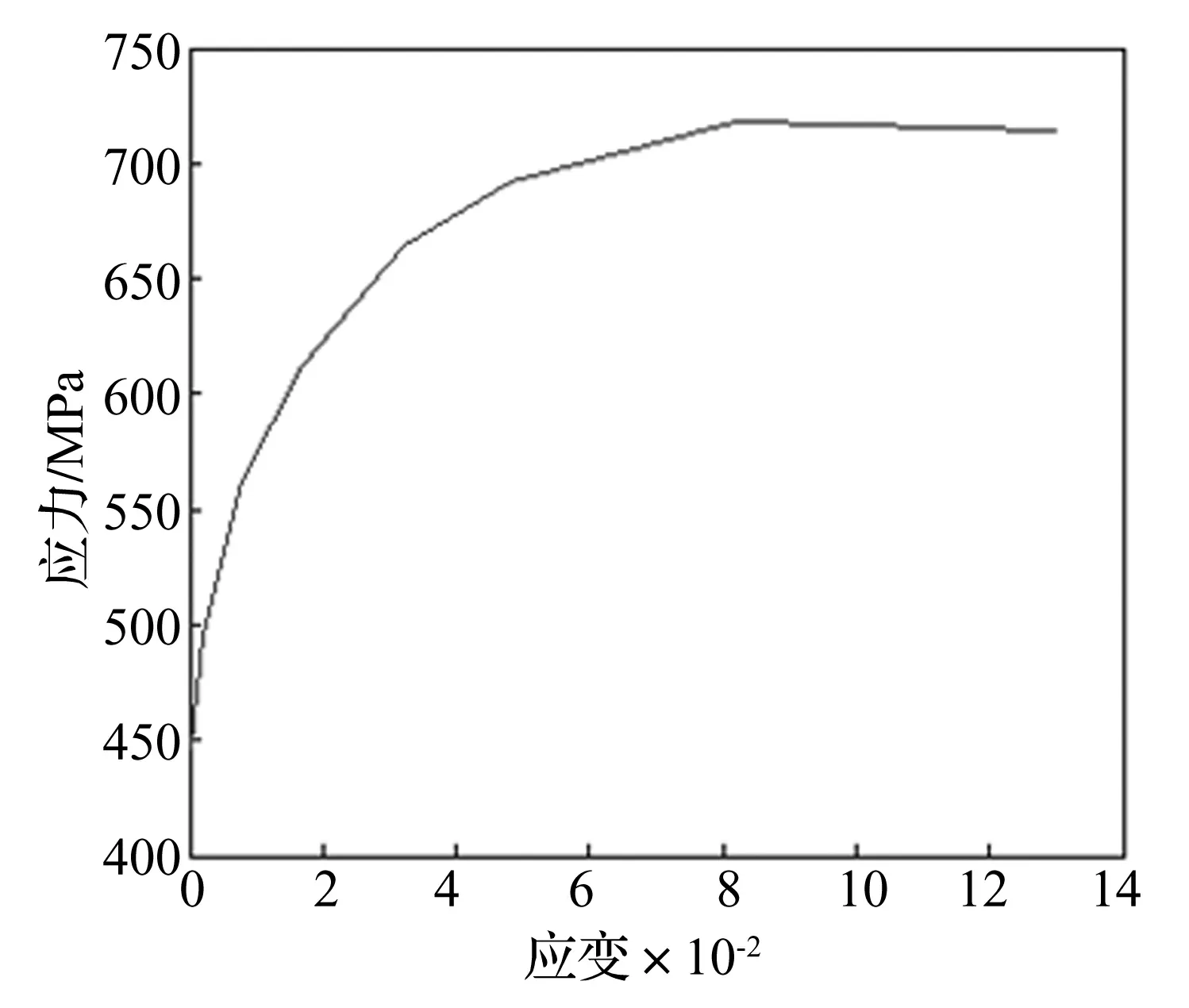
图2 应力—应变关系曲线Fig.2 Curve of stress vs. strain

2.2 模型改进

诱导结构是薄壁构件应力集中的地方，使结构的屈曲变形稳定。为了提高原模型在碰撞过程中的抗撞性能，本文对原模型结构做了改进，沿光滑表面的薄壁结构(原模型结构尺寸不变)分别添加圆弧形诱导凹槽、凸槽及凸凹交替的圆弧形诱导槽。对于凸凹交替的诱导槽为了获得对称变形模式，诱导槽个数应为奇数个，且第一个为凸槽。根据原模型几何长度，如图3所示在每种结构上分别设置3个诱导槽，r、h1、h2分别为诱导槽半径、槽端距和槽间距，均为动态设计变量。以诱导槽半径r∈[0.8,2.4]mm，槽端距h1∈[10,60]mm，槽间距h2∈[10,36]mm作为试验因素。针对以上3种不同结构的诱导槽，各选择具有不同半径、槽端距及槽间距有代表性的18个样本点(见表2)。

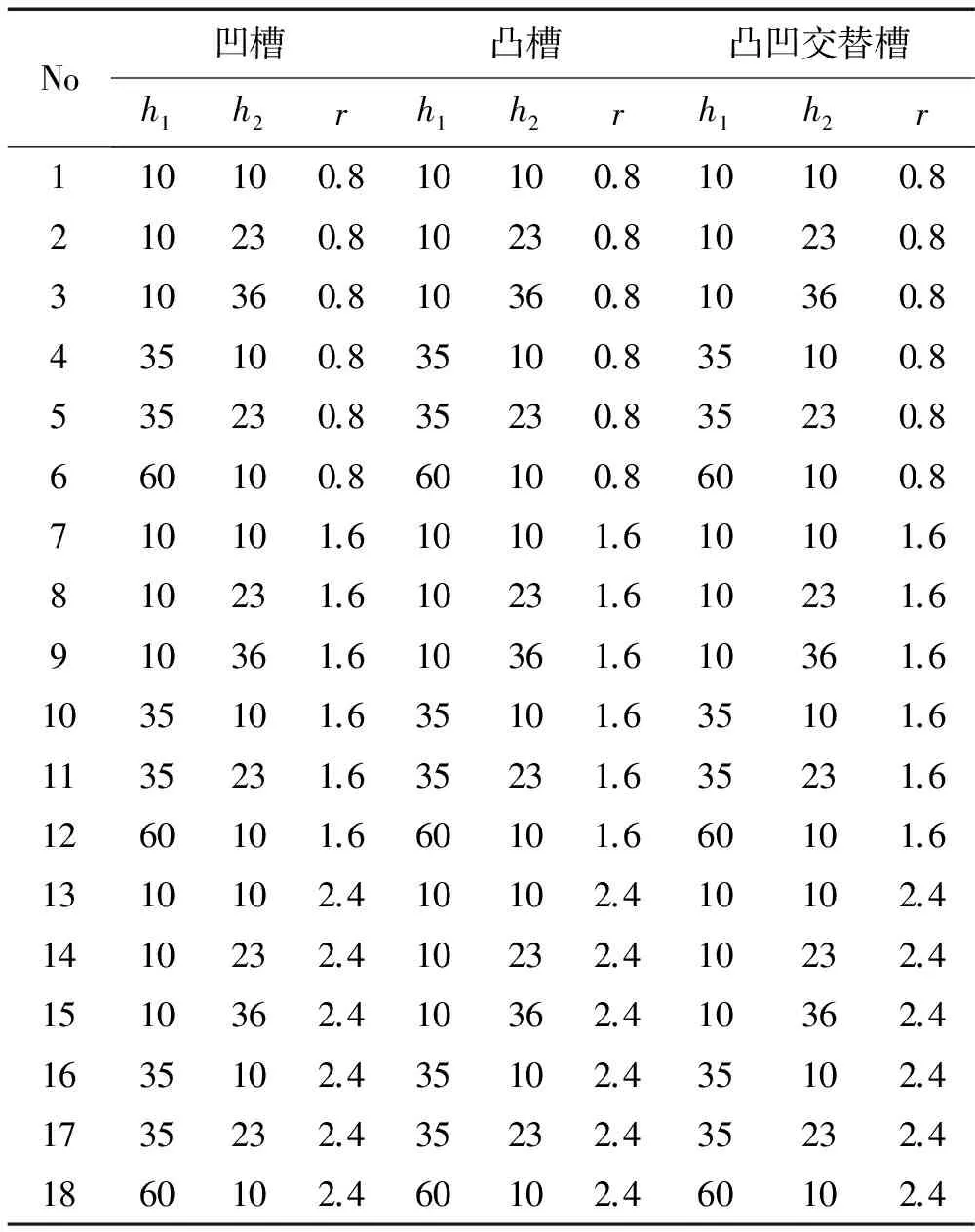
表2 3种诱导槽结构样本点

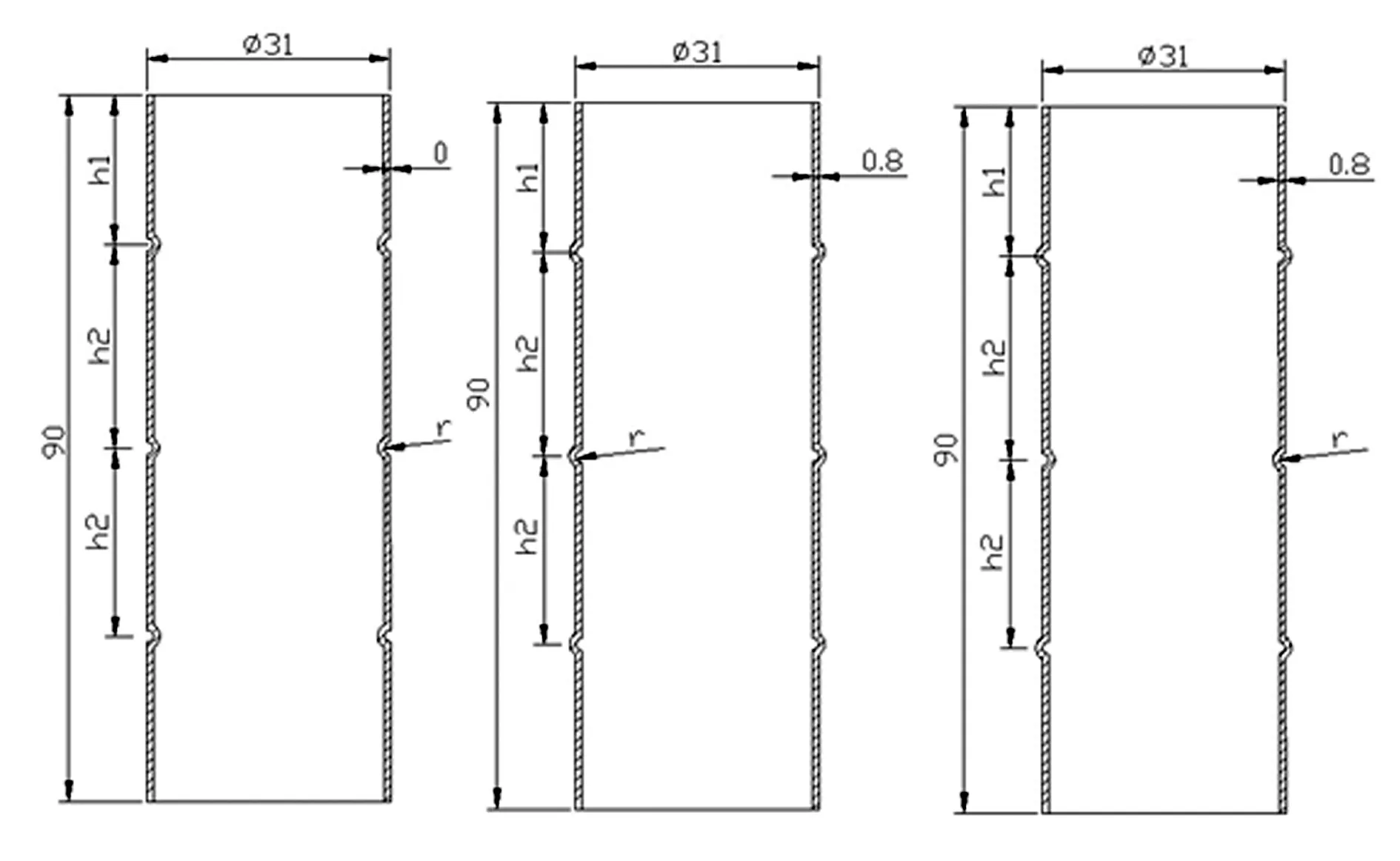
图3 改进结构模型Fig.3 The improved structural model

前文已对原模型有限元分析结果与文献上的实验值进行了对比，验证了有限元分析的可靠性。为了节约资源，本文分别对3种具有不同诱导结构薄壁构件设计样本点进行有限元分析计算，从而得到其碰撞响应。

该多目标优化问题数学表达式可进一步表示为

(4)

3 径向基函数法优化设计

3.1 径向基函数模型

径向函数[9-12]是以预测点与样本点间的欧氏距离为自变量的一族函数。以径向函数为基函数，通过线性组合构造出来的近似模型即为径向基函数模型。

在设计空间中，关于设计变量的响应函数的近似表达式可以定义为

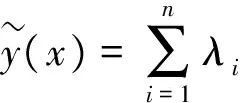
(5)

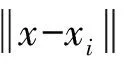
将n个样本点及每个样本点对应的响应函数值代入到公式(5)，可以得到方程组矩阵形式为

Y=Φλ

(6)

在得到响应函数的径向基函数模型后，需要对近似模型精度进行验证，通过额外测试点(不包括样本点)决定系数R2和误差平方和均方根RMSE来验证径向基函数模型对设计变量的拟合情况。决定系数R2和误差平方和均方根RMSE分别定义为

(7)

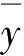
3.2 理想点法求解多目标优化问题

多目标优化问题在数学上一般可表示为

(8)

在式(8)中，先求解p个单目标问题

j=1,2,…,p

(9)

(10)

然后极小化φ[f(x)]，即求解

(11)

并将它的最优解x*作为式(8)在这种意义下的最优解。

对于多目标优化问题采用理想点法易得到较明确的全局最优值，于是本文的多目标优化问题可进一步表示为

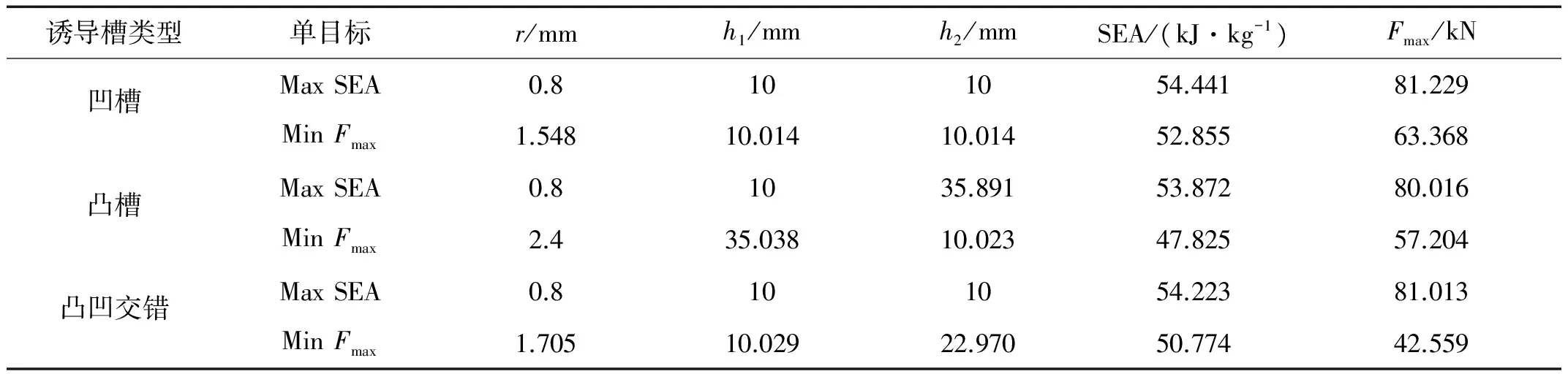
(12) 表3 SEA和Fmax两个单目标函数优化值

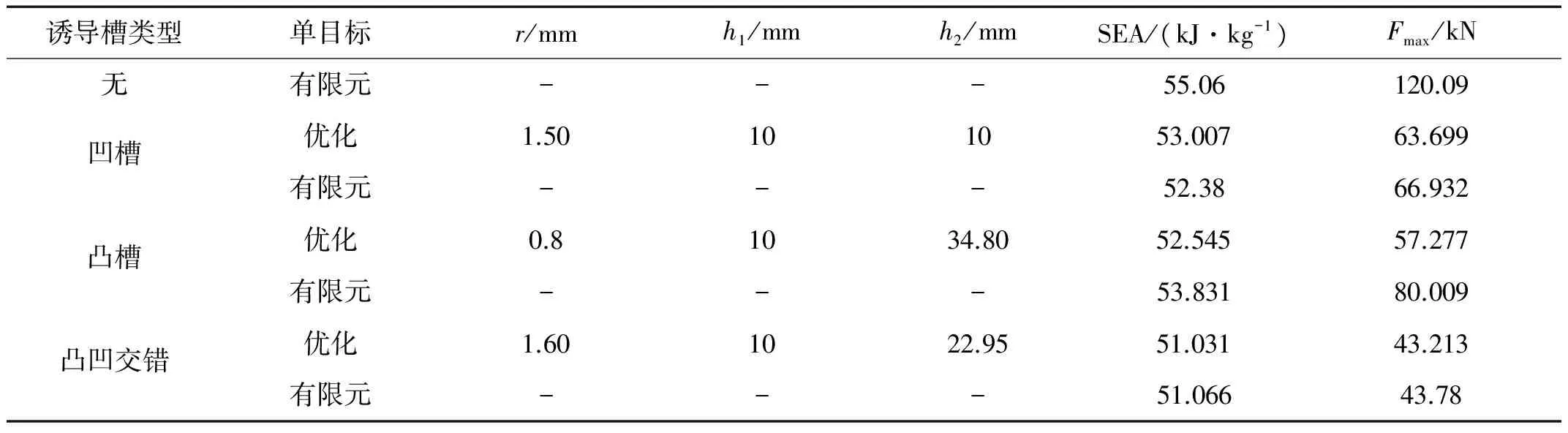
表4 多目标优化结果与有限元结果对比

3.3 优化结果

对于带有圆弧形诱导槽的薄壁构件，诱导槽半径r和槽端距h1、槽间距h2是影响结构抗撞性能的3个重要参数，通过有限元计算得到了具有不同诱导槽结构样本点的碰撞响应，从而得到SEA和Fmax关于设计变量r、h1、h2的响应函数。

图4 优化后薄壁结构模型Fig.4 Optimized the thin-walled structure models

表3分别给出了3种诱导槽结构关于SEA和Fmax两个单目标函数的优化值，可见两个单目标函数分别有不同的优化解，两个目标函数很难同时达到最优。故针对上述3种不同诱导槽结构我们采用理想点法对式(12)的多目标优化问题进行了求解，分别得到3种诱导槽结构的最优设计参数，并将相应参数带入其有限元模型中进行计算以验证参数的有效性，同时与原模型的有限元结果进行对比(见表4)。从表4中可以看出3种诱导槽结构的优化值与有限元分析结果的误差很小，进一步说明了径向基函数模型和理想点优化方法的有效性，满足工程设计的要求。

如图4分别给出具有圆弧形诱导凹槽、凸槽及凸凹交替的诱导槽其最大的SEA、最小的Fmax和理想点法计算得到多目标问题的优化结构。

图5、图6分别给出了该多目标问题达到最优时，诱导凹槽、凸槽及凸凹交替的诱导槽在碰撞过程中冲击载荷和吸收能量随压溃位移和压溃时间变化情况，并将其与相应条件的原模型进行比较。从冲击载荷图5可以看出，优化后3种诱导槽结构最大峰值碰撞力均低于无诱导槽结构，分别降低约44.27%、33.38%和63.54%，其中最大峰值碰撞力降低最明显的情况出现在凸凹交替的诱导槽结构；从吸收能量图6可以看出，3种诱导槽结构所吸收的能量并没有很大的减少，在碰撞时间为10 ms时，3种结构所吸收的能量与同时间原模型吸收的能量比较相近了；由表4可知，由于施加诱导槽造成结构整体质量增加，导致3种诱导槽结构的SEA值分别降低4.87%、2.23%和7.25%，与大幅降低的最大峰值碰撞力相比，很好地达到了提高抗撞性的目标。可见增加圆弧形诱导槽结构在不影响原模型吸能的情况下，显著地降低了最大峰值碰撞力。

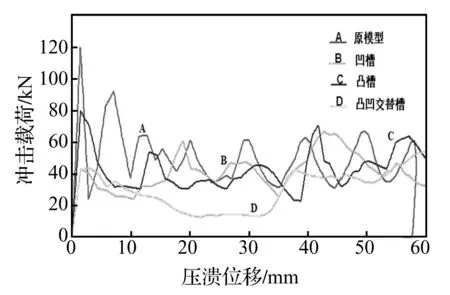
图5 冲击载荷随压溃位移变化对比曲线Fig.5 Comparison curve of axial force-crushing vs. displacement

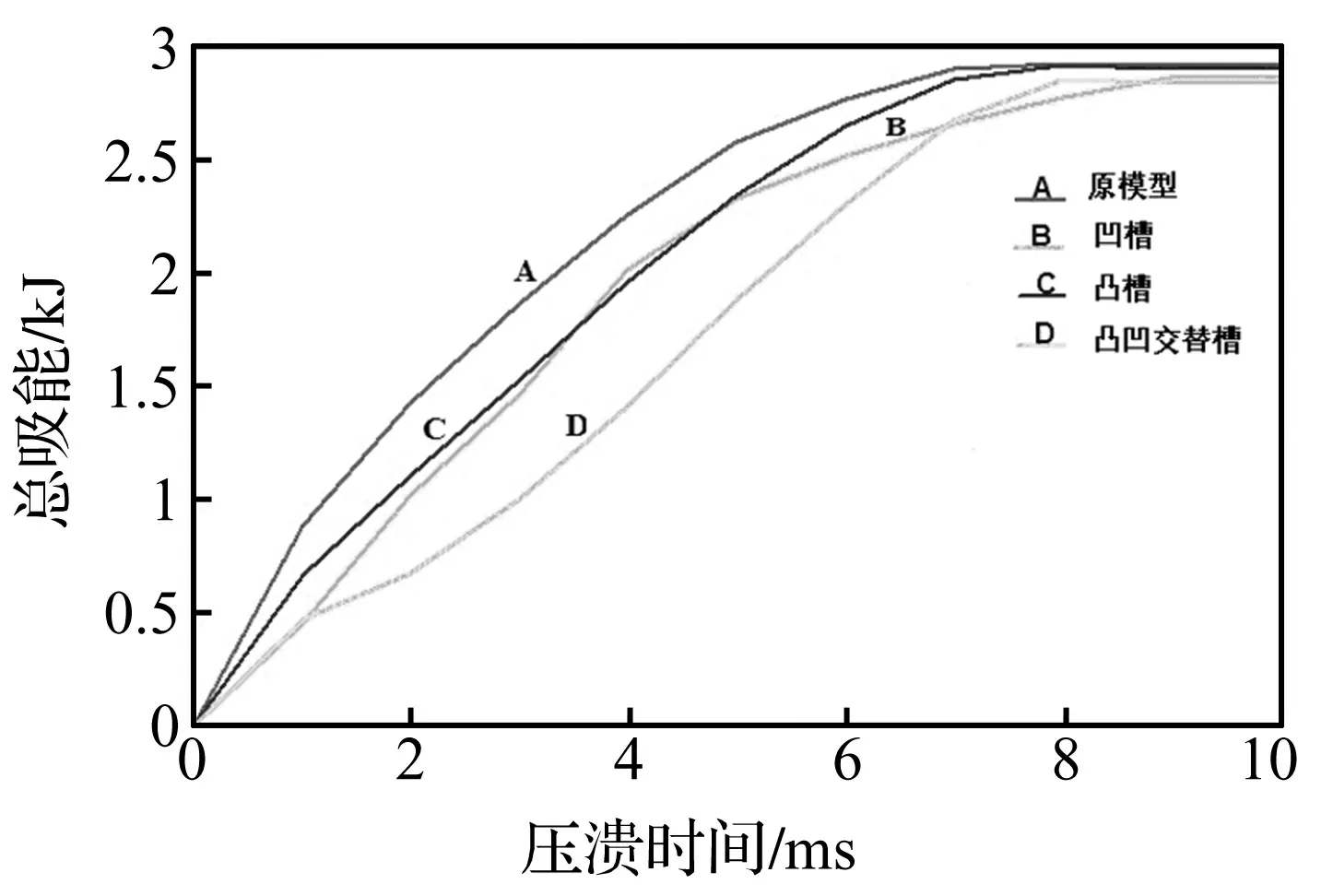
图6 吸收能量随冲击时间变化对比曲线Fig.6 Comparison curve of absorbing energy vs. time

优化后3种诱导槽结构在碰撞过程中发生叠缩变形如图7所示，这种变形模式有利于结构在变形过程中吸收更多的碰撞动能，这是由于塑性变形首先在诱导槽处开始，大部分的冲击能在诱导槽处以塑性变形的方式被吸收。可见增加圆弧形诱导槽结构后，可大大提高薄壁构件的抗撞性能。

图7 优化后构件叠缩变形Fig.7 Progressive folding deformation of optimal component

4 结 论

本文对薄壁圆管构件进行了改进，引入了3种不同形式的圆弧形诱导槽，建立了以比吸能和最大峰值碰撞力为评价指标的多目标优化问题数学模型，研究诱导槽半径、槽端距和槽间距对抗撞性能的影响。数值分析的结果表明：3种不同形式的圆弧形诱导槽结构均实现了在保证不减少薄壁构件吸能能力的情况下达到了明显减小最大峰值碰撞力的目的，诱导槽半径、槽端距和槽间距对薄壁构件的比吸能和最大峰值碰力的影响很大。优化结果表明：与原模型相比优化后3种诱导槽结构的最大峰值碰撞力均大幅度的降低了，其中凸凹交替的诱导槽结构降低的最为显著达到了63.54%，有效的保证了碰撞过程中乘员的安全性；从吸能角度来看，3种诱导槽结构所吸收的能量并没有很大减少，在碰撞时间为10 ms时所吸收的能量达到了与同一时间原模型吸收的能量；就比吸能而言与原模型相比凸凹交替诱导槽结构减少最多也仅为7.25%，显然诱导槽结构对最大峰值碰撞力的改善要优于比吸能。可见3种不同形式的圆弧形诱导槽均大大提高了薄壁构件的抗撞性，此方法为进一步研究实际吸能构件的抗撞性设计提供思路。

[ 1 ] 亓昌,董方亮,杨姝,等.锥形多胞薄壁管斜向冲击吸能特性仿真研究[J].振动与冲击,2012,31(24):102-107. QI Chang, DONG Fang-liang, YANG Shu, et al. Energy-absorbing characteristics of a tapered multi-cell thin-walled tube under oblique impact[J]. Journal of Vibration and Shock, 2012, 31(24) : 102-107.

[ 2 ] Avalle M, Chiandussi G. Optimization of a vehicle energy absorbing steel component with experimental validation[J]. International Journal of Impact Engineering, 2007, 34(4): 843-858.

[ 3 ] Shakeri M, Mirzaeifar R, Salehghaffari S. New insights into the collapsing of cylindrical thin-walled tubes[J]. Mechanical Eengineering Science, 2007, 221(8):869-885.

[ 4 ] Cho Y B, Bae C H, Suh M W, et al. A vehicle front frame crash design optimization using hole-type and dent-type crush initiator[J]. Thin-Walled Structures, 2006, 44(4): 415-428.

[ 5 ] 张涛，刘土光，肖汉林，等.高速冲击下薄壁组合结构吸能特性研究[J]. 爆炸与冲击，2006， 26(5)：395-403. ZHANG Tao, LIU Tu-guang, XIAO Han-ling, et al. Energy absorption performance of thin-walled structures with triggering holes subjected to high-speed axial impact[J]. Explosion and Shock Waves, 2006, 26(5): 395-403.

[ 6 ] 王海亮，林忠钦，金先龙. 基于响应面模型的薄壁构件耐撞性优化设计[J]. 应用力学学报，2003，20(3)：61-66. WANG hai-liang, LIN zhong-qin, JIN xian-long. Optimal design of thin-walled sections for structural crashworthiness based on the response surface model[J]. Chinese Journal of Apllied Mechanics, 2003, 20(3): 61-65.

[ 7 ] Jin S Y, Altenhof W. Comparison of the load/displacement and energy absorption performance of round and square AA6061-T6 extrusions under a cutting deformation mode[J].International Journal of Crashworthiness, 2007,12(3): 265-278.

[ 8 ] Tai Y S, Huang M Y, Hu H T. Axial compression and energy absorption characteristics of high-strength thin-walled cylinders under impact load [J]. Theoretical and Appied Fracture Mechanics, 2010, 53(1):1-8.

[ 9 ] Fang H, Rais- Rohani M, Liu Z, et al. A comparative Study of metamodeling methods for multiobjective crashworthiness optimization[ J]. Computers and Structures, 2005, 83(25-26): 2121- 2136.

[10] Jin R, Chen W, Simpson T W. Comparative studies of metamodeling techniques under multiple modelling criteria[J]．Structural and Multidisciplinary Optimization，2001，23(1):1-13.

[11] Rais-Rohani M, Singh M N. Comparison of global and local response surface techniques in reliability-based optimization of composite structures[J]. Struct Multidisciplinary Optim., 2004,26(5):333-345.

[12] Fang H B, Wang Q. On the effectiveness of assessing model accuracy at design points for radial basis functions[J] .Commun. Numer. Methods Eng.,2008,24(3):219-235.

Crashworthiness design optimization of thin-walled cylinders with different inducing grooves

TAN Li-hui1,2, TAN Hong-wu3, MAO Zhi-qiang4，CUI Xiao-mei1,2, XU Tao1

(1. College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China;2. College of Mechatronic Engineering, Jilin Institute of Chemical Technology, Jilin 132022, China; 3. Orgainic Synthesic Factory Petro China Jilin Petrochemical Company, Jilin 132022, China；4. Refinery Factory, PetroChina Jilin Petrochemical Company, Jilin 132022, China)

Metal thin-walled cylinders with different inducing grooves were taken as a study object. The maximization of the specific energy absorption (SEA) and the minimization of the maximum peak impact force (Fmax) of the cylinders were chosen as the evaluation indexes and radius of inducing grooves, distance between inducing grooves and free end, and distance between inducing grooves were chosen as design variables to establish a multi-objective optimization model. The finite element code LS-DYNA was adopted to compute the impact responses of the cylinders with different inducing grooves. Furthermore, an approximate objective function was constructed with the radial basis functions (RBFs), the optimal design was performed by using the ideal point method and considering the effects of inducing convex grooves, inducing concave ones and concavo-convex ones on SEA andFmax. After the optimization, the optimal values of inducing groove radius, diatance between inducing groove and free end, and distance between inducing grooves were obtained. Thus, the ideal and optimal structures for inducing grooves were achieved.

thin-walled cylinders; specific energy absorption (SEA); maximum peak impact force (Fmax); crashworthiness; inducing grooves

国家自然科学基金项目(50975121)；吉林省科技发展计划项目(201101030)；一汽集团科技创新项目“乘用车碰撞概念模型建立与优化分析”(1332)

2013-09-23 修改稿收到日期：2013-11-28

谭丽辉 女，博士生，1977年生

徐涛 女，教授，博士生导师，1955年生

TH123.1

A

10.13465/j.cnki.jvs.2014.08.004