水下夹芯复合空腔结构声学特性试验研究
2014-08-11罗忠,周欣
罗 忠, 周 欣
(1. 海军工程大学 科研部, 武汉 430033;2. 海装驻上海地区军事代表局, 上海 201206)
水下夹芯复合空腔结构声学特性试验研究
罗 忠1, 周 欣2
(1. 海军工程大学 科研部, 武汉 430033;2. 海装驻上海地区军事代表局, 上海 201206)
引入空腔改善夹芯复合结构低频段吸声性能。建立了三种典型水下声隐身结构声学系统模型,在数值分析吸声性能影响因素基础上,运用脉冲声管试验方法,分析了空气背衬“硬”边界条件和水背衬“软”边界条件下,有无空腔试样、不同空腔间距、空腔形状和深度对谐振吸声峰值及峰值频率等的影响。试验结果表明,空腔显著改善了夹芯复合结构低频段吸声性能;空气背衬下,空腔间距越小,首阶谐振吸声峰值越大,峰值频率越低,水背衬条件下则相反;空腔体积越大,首阶谐振吸声峰值越小,峰值频率越低。
夹芯复合结构;空腔;吸声系数;谐振;试验
随着潜艇巡航深度的增大和声纳探测技术的不断发展,对潜艇的声隐身技术提出了新的挑战,水下声隐身结构正朝着耐压、低频和宽频段吸收的方向发展。夹芯复合声隐身结构是一种新型水下声隐身结构,由比强度高、比刚度大、阻尼性能好、透声性能优异、成型工艺简单的纤维增强复合材料表层和吸声高分子芯材组成,可以代替原有“钢结构+吸声覆盖”的吸声结构,实现水下目标承载和声隐身的一体化设计[1-3]。在单一均质材料中引入谐振空腔,能够较好地改善低频段吸声性能,带周期阵列空腔消声覆盖层已得到了广泛应用[2-9]。传统的对周期空腔阵列消声覆盖层声学性能分析方法有传递矩阵法[3-4]、有限元法[2,4-7]、等效参数法[8-9]等,但由于夹芯复合空腔结构中有多种吸声机理并存,数值方法仅能从定性角度对空腔深度、直径、间距、位置、形状等几何参数的影响规律进行分析,驻波声管和消声水池试验成本较大,所以本文采用脉冲声管试验方法,结合多种吸声机理的影响,分析夹芯复合空腔结构几何参数对吸声性能的影响,并获得了较好的低频段吸声性能。应该说,这些研究工作主要是新型水下夹芯复合空腔结构的初步探讨,或者是在模型试验基础上,对理论研究规律的验证,还需要根据探索出的吸声机理对夹芯复合空腔结构进行深入的优化设计。
1 理论分析

图1 典型声隐身夹芯复合空腔结构Fig.1 The typical acoustic stealth sandwich composite structure with cavum
典型夹芯复合空腔结构见图1,由玻璃钢表层、吸声材料和空腔等组成。水下声隐身结构声学系统简化模型见图2。图2(a)模型Ⅰ与单壳体水下目标声学环境相似,能够采用有限元方法分析空腔谐振规律,也可以采用脉冲声管进行试验验证。图2(b)模型Ⅱ为无限水背衬条件,与声隐身实心舵和稳定翼等凸出部位的实际声学环境相似,能够采用有限元方法分析空腔谐振规律;消声水池和驻泊声管的背衬均为尖劈吸声材料,与模型Ⅱ声学系统相同,但试验成本较大;脉冲声管试验成本较小,但由于声管直径较小,难以布设尖劈吸声材料,模型Ⅱ很难进行脉冲声管试验验证。图2(c)模型Ⅲ为耐压壳体和空气背衬条件,与水下目标船体的实际声学环境最相近,也易于进行声管试验分析;但于吸声结构与耐压壳体之间存在较厚的中间水层,透过吸声材料的声波会和空气背衬反射的声波叠加,在中间水层形成谐振声波,对理论分析带空腔吸声结构的谐振频率和带宽时,难以区分声波叠加后的谐振和空腔引起的谐振, 一般很少采用模型Ⅲ进行带空腔
吸声结构的谐振规律分析。因此,在理论分析水下夹芯复合空腔结构声学特性时,采用模型Ⅰ和模型Ⅱ;在进行脉冲声管试验分析时,采用模型Ⅰ和模型Ⅲ。
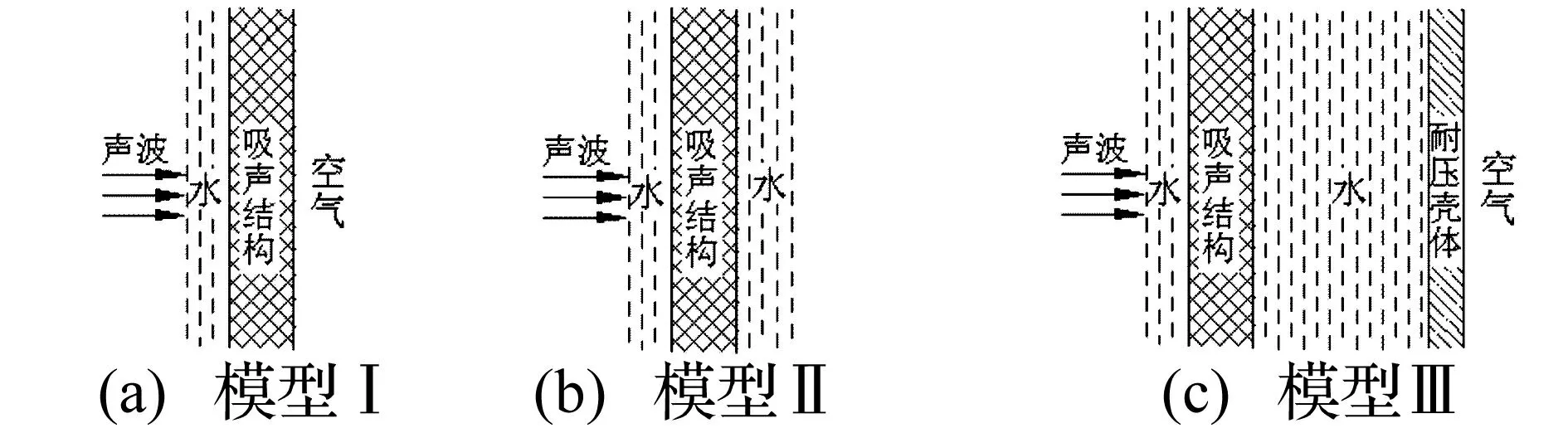
图2 水下声隐身结构声学系统简化模型Fig.2 The simple acoustic model of underwater stealth structure
带空腔吸声结构的吸声机理非常复杂,涉及材料粘弹性损耗、空腔谐振、波型转化、散射等多种因素,关于带空腔吸声结构吸声性能的计算方法较多,有分层介质理论[3-4]、多次散射逼近法[8]、等效参数反演法[9]、基于Block-Floquet周期边界条件的有限元法[4-6,10-11]等方法。在夹芯复合结构中引入空腔,其谐振吸声机理由两部分组成[2]:① 空腔侧壁沿结构法线方向或径向的振动,而且这两种振动的频率特性曲线最大值略有偏移,使吸声结构在声波入射下得到较宽的谐振吸声频带;② 整个夹芯复合吸声结构在声波作用下整体的弯曲振动,又形成另外一个谐振吸声系统。本文采用经过算例和试验验证的有限元计算方法[2],设计夹芯复合空腔结构,并通过脉冲声管试验对其声学性能进行验证,检验不同背衬条件下夹芯复合空腔结构的吸声特性。

图3 模型Ⅰ中夹芯复合空腔结构声学特性频响Fig.3 The frequency response of acoustic properties for sandwich composite structure with cavum in model Ⅰ

图4 模型Ⅱ中夹芯复合空腔结构声学特性频响Fig.4 The frequency response of acoustic properties for sandwich composite structure with cavum in model Ⅱ
夹芯复合空腔吸声结构内含10 mm直径圆柱型空腔,间隔20 mm,正方形网格排列,空腔腔体位于背声面芯材底部。模型Ⅰ和模型Ⅱ,有无圆柱空腔、空腔间距、空腔形状对声学特性频响见图3和图4。可以看出,① 带空腔的吸声层声学特性在3.5 kHz、4.3 kHz、8.2 kHz多个频带较宽的谐振吸声峰值,空腔显著改善了低频吸声特性;② 模型Ⅰ为空气背衬的“硬”边界条件,随着空腔间距的减小, 首阶谐振吸声峰值增大, 峰值频率往低频移动约0.2 kHz,这是由于空腔间距减小,单位体积内空腔体积比增大,在全反射边界条件下模型整体弯曲刚度降低引起的;圆柱形空腔体积最大、刚度最小,圆锥形空腔体积最小、刚度最大,随着空腔体积增大,模型Ⅰ首阶谐振吸声峰值和带宽减小,峰值频率往低频移动了0.6 kHz,这与文献[4]研究规律一致。③模型Ⅱ为水背衬的“软”边界条件,随着空腔间距的减小,首阶谐振吸声峰值和带宽略微减小,峰值频率往高频移动了0.7 kHz,与模型Ⅰ规律相反,且变化更敏感,这是由于间距减小、单个空腔刚度增大引起的;模型Ⅱ随着空腔体积增大,首阶谐振吸声峰值和带宽减小,峰值频率往低频移动了0.3 kHz,与模型Ⅰ规律和影响幅度基本相同。
2 试验模型
夹芯复合空腔结构声学性能试验采用脉冲声管测试系统进行,由于声学测试系统采用的是圆柱型试样,所以无法对空腔的间距进行精确的控制,只能通过调节单个试样中空腔的个数来控制间距。夹芯复合空腔试样见表1,试样直径均为56.3 mm,上、下表层玻璃钢厚度均为4 mm,吸声芯层均采用聚氨酯改性环氧基微珠增强吸声体,厚度为25 mm。试验采用声学系统模型Ⅰ和模型Ⅲ,模型Ⅲ中试样位于声管中部,距管口钢背衬1.8 m。
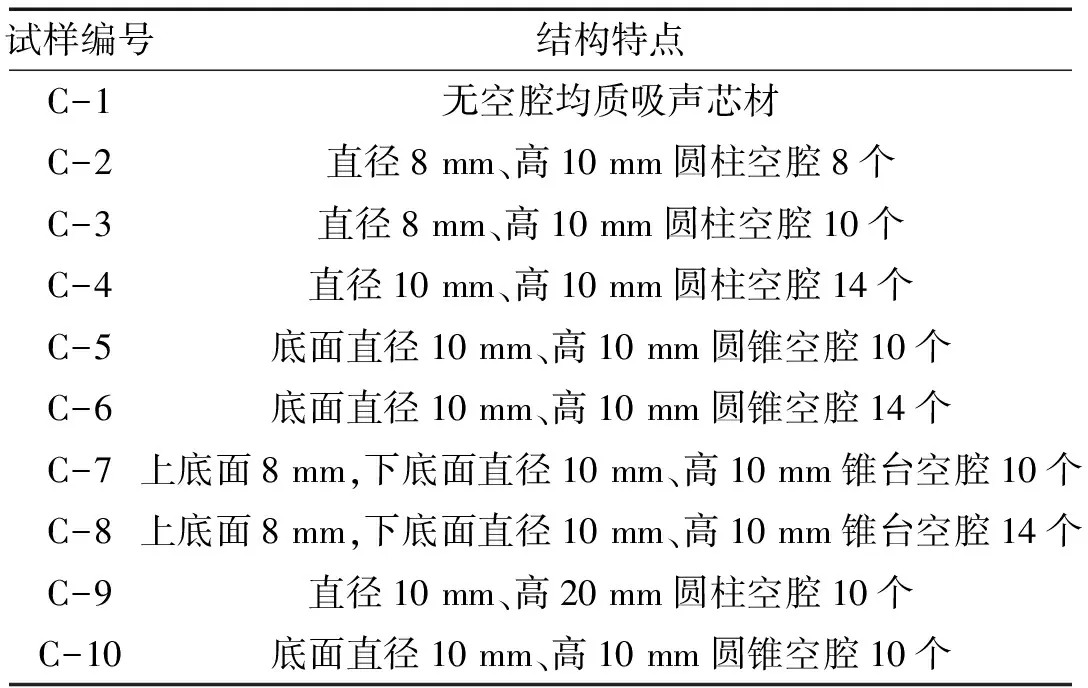
表1 夹芯复合空腔结构试样主要参数
夹芯复合空腔结构试验模型空腔布置如图5所示,试验模具和未粘贴玻璃钢试样如图6所示。

图5 夹芯复合空腔结构试样腔体分布Fig.5 The distributing of cavum of experimental model of sandwich composite structure

图6 夹芯复合空腔结构制作模具和试样Fig.6 The experimental mould and specimen of sandwich composite structure with cavum
采用脉冲法数字测量装置,由位于脉冲管一端的换能器向管中发射脉冲声波,声波经试样或另一端背衬反射,由同一换能器接收,测量频率间隔为200 Hz。在测量频率点上,应用信号采集器先测量并记录带试样的反射信号相对应的电信号,然后测量并记录与标准反射体的反射电信号,经DFT处理后得到它们的幅度和相位,最后计算反射系数的模和相位,进而计算出吸声系数。
为验证试验结果的稳定性,5#样品和10#样品结构参数相同,按模型Ⅰ和模型Ⅲ条件测试吸声系数见图7。可以看出:① 模型Ⅰ条件下,两个样品在2-6 kHz频段吸声系数吻合较好,并均在6 kHz附近出现谐振峰值,在高频段吸声系数有一定差异,这是由于试样为逐个浇注,工艺及环境条件对基体高频吸声性能产生一定影响;② 模型Ⅲ条件下,两个试样在2 kHz附近均出现较高的谐振峰值,且吻合较好;③ 两种模型条件下的吸声系数测试结果较稳定,可以采用此试验方法分析夹芯复合空腔结构谐振特性。
3 试验结果分析
3.1 模型Ⅰ试验结果
模型Ⅰ条件下,均质层状夹芯复合试样与带空腔试样吸声系数测试结果比较见图8。可以看出:含14个圆柱空腔试样和含14个锥台空腔试样吸声系数频谱上均出现了明显的谐振现象,且空腔体积越大,谐振峰值往低频移动,与理论分析规律一致。当空腔体积足够大、空腔个数足够多时,在吸声系数频响曲线上能看出完整的谐振吸声峰值和带宽,如锥台型空腔的谐振峰值在5 kHz附近;圆柱型空腔在6 kHz附近出现一个较小的谐振吸声峰值,在11 kHz附近出现较高的谐振吸声峰值,且8-12 kHz频段内只有半个带宽,可见空腔有效的改善了均质层状夹芯复合结构低频吸声不足。由于圆柱形试样空腔间距及材料参数原因,造成了峰值位置与数值计算存在一定差异。
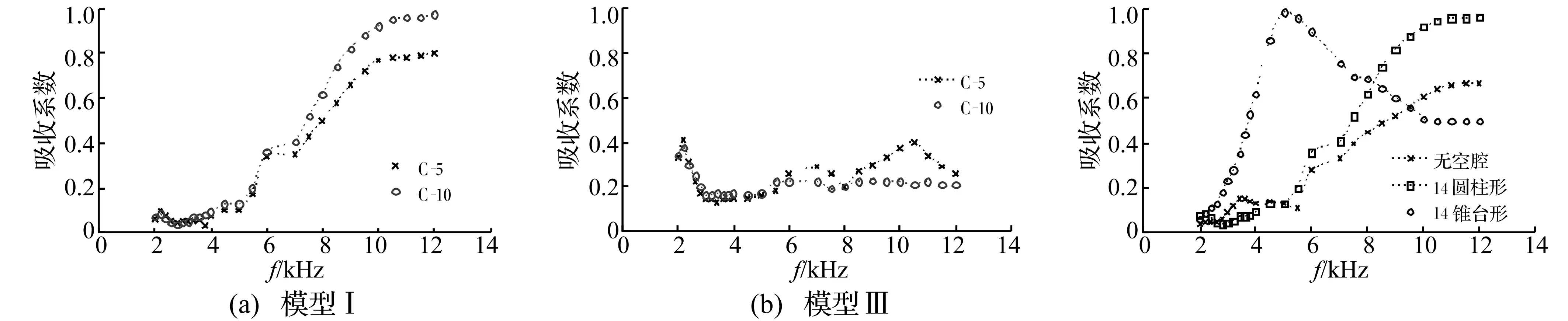

图7 脉冲声管试验吸声系数稳定性比较Fig.7Thestabilityofexperimentalabsorptioncoefficient图8 模型Ⅰ无空腔与有空腔比较Fig.8ThecontrastofhomosphereandwithcavumSandwichcompositestructureinmodelⅠ
圆柱型、圆锥型、锥台型空腔间距对吸声系数频响分别见图9、图10和图11。可以看出:① 都于圆柱形空腔,空腔间距在低频段对吸声性能影响不大,但在5 kHz以上频段,随着空腔间距减小,谐振吸声峰值增大,峰值频率稍往低频移动。② 对于圆锥型空腔试样,随着空腔间距减小,6 kHz附近谐振峰值变化不大,在11 kHz附近谐振吸声峰值稍增大,峰值频率稍往低频移动,分析这是由于圆锥型空腔体积较小,且圆锥空腔在声波作用下只有壁面的弯曲振动模式,三角形壁面相对弯曲刚度又较高,弯曲振动变形较小,不能有效的吸收声能。③ 空腔间距对锥台型空腔试样影响显著,随着间距减小,吸声峰值增大,峰值频率往低频移动,吸声带宽减小。④试验结果与理论分析规律一致,夹芯复合空腔结构的谐振吸声性能,除与空腔间间距有关外,还与空腔体积及芯材的材料参数关系较大。
图12和图13为模型Ⅰ条件下空腔形状对吸声性能频响。可以看出:当试样中空腔数为10个时,吸声系数在6 kHz和11 kHz附近出现两个谐振吸声峰值,随着空腔体积的增大,峰值也增大,峰值频率稍往低频移动,吸声带宽也增大;圆台型空腔体积最大,当试样中空腔数为14个时,能够看到出现完整的谐振吸声峰值。


图9 模型Ⅰ圆柱型腔空腔间距影响Fig.9TheaffectofabsorptioncoefficientfordifferentcolumncavumintervalinmodelⅠ图10模型Ⅰ圆锥型腔空腔间距影响Fig.10TheaffectofabsorptioncoefficientfordifferenttapercavumintervalinmodelⅠ图11 模型Ⅰ锥台型腔空腔间距影响Fig.11TheaffectofabsorptioncoefficientfordifferentconecavumintervalinmodelⅠ


图12 模型Ⅰ空腔形状影响(10个空腔)Fig.12TheaffectofabsorptioncoefficientfordifferentcavumshapeinmodelⅠ(10cavum)图13 模型Ⅰ空腔形状影响(14个空腔)Fig.13TheaffectofabsorptioncoefficientfordifferentcavumshapeinmodelⅠ(14cavum)图14 模型Ⅰ圆柱腔空腔深度影响Fig.14TheaffectofabsorptioncoefficientfordifferentcolumncavumdepthinmodelⅠ
图14为空气背衬下14个圆柱型空腔的腔体深度对吸声系数频响,由图可见:腔体深度越大,2-12 kHz频段吸声性能越优,且谐振吸声峰值增大,峰值频率往低频移动,但谐振带宽却减小,这是因为空腔高度增大,侧壁的弯曲刚度减小,因此侧壁的弯曲振动频率降低。
3.2 模型Ⅲ试验结果
模型Ⅲ条件下,均质层状夹芯复合试样与带空腔的夹芯复合试样吸声系数试验结果见如图15,空腔的引入有效改善了夹芯复合结构的吸声性能,圆柱型和锥台型空腔试样吸声系数频响曲线上均出现了谐振吸声峰值,随着空腔体积的增大,峰值位置往低频移动。
圆柱型、圆锥型、锥台型空腔间距对吸声系数频响分别见图16、图17和图18。可以看出,空腔间距减小,谐振吸声峰值变密,在大部分频段内试样吸声系数均得到提高,这是由于空腔数增多,谐振模态增多而引起的。同时,随着空腔间距减小,圆锥型空腔试样首阶谐振峰值增大,峰值频率往高频移动,谐振带宽也增大;而体积最大的锥台型空腔试样首阶谐振峰值减小,且在高频段吸声系数较大。


图15 模型Ⅲ无空腔与有空腔比较Fig.15ThecontrastofhomosphereandwithcavumSandwichcompositestructureinmodelⅢ图16 模型Ⅲ圆柱型腔空腔间距影响Fig.16TheaffectofabsorptioncoefficientfordifferentcolumncavumintervalinmodelⅢ图17 模型Ⅲ圆锥型腔空腔间距影响Fig.17TheaffectofabsorptioncoefficientfordifferenttapercavumintervalinmodelⅢ


图18 模型Ⅲ锥台型腔空腔间距影响Fig.18TheaffectofabsorptioncoefficientfordifferentconecavumintervalinmodelⅢ图19 模型Ⅲ空腔形状影响(10个空腔)Fig.19TheaffectofabsorptioncoefficientfordifferentcavumshapeinmodelⅢ(10cavum)图20 模型Ⅲ空腔形状影响(14个空腔)Fig.20TheaffectofabsorptioncoefficientfordifferentcavumshapeinmodelⅢ(14cavum)
图19和图20为空腔形状对吸声系数试验频响。可以看出:与空气背衬下结果相反,随着空腔体积的增大,吸声系数越低,模型Ⅲ条件水背衬下透射也越大,谐振吸声效率越低,进入吸声芯层的声能没有得到有效的吸收;同时随着空腔体积的增大,首阶谐振峰值减小,峰值频率往低频移动,谐振带宽也减小,与理论分析规律一致。

图21 模型Ⅲ圆柱腔空腔深度影响Fig. 21 The affect of absorption coefficient for different column cavum depth in model Ⅲ
图21为圆柱型空腔腔体深度对吸声系数试验频响。由图可见:随着腔体深度的增大,首阶谐振吸声峰值频率往低频移动,由于2kHz以下频段吸声系数未能测出,所以看不出吸声峰值是否增大,但可以明显看出次阶谐振吸声峰值增大,在3-9 kHz频段,吸声性能得到改善。
4 结 论
(1) 空腔引入有效改善了夹芯复合结构低频段吸声性能,夹芯复合空腔结构声学性能试验结果与理论分析规律一致。
(2) 空气背衬“硬”边界条件下,随着空腔间距减小,首阶谐振吸声峰值增大,峰值频率往低频移动;水背衬“软”边界条件下则相反。
(3) 随着空腔体积增大,首阶谐振吸声峰值和带宽减小,峰值频率往低频移动。
[ 1 ] John H, Di S C. Composite structure[P]. Britain patent: PCT/GB1998 /01377, 1997.
[ 2 ] 罗忠,杨坤. 水下夹芯复合空腔结构声学特性计算方法研究[J]. 振动与冲击, 2013, 32(8):147-152. LUO Zhong, YANG Kun. Acoustic property computing method for an underwater sandwich structure with cavum[J]. Journal of Vibration and Shock, 2013, 32(8):147-152.
[ 3 ] 罗忠,朱锡,简林安,等. 斜入射下水中隐身夹芯复合材料附体结构声学设计[J]. 振动与冲击, 2009, 28(5):49-54. LUO Zhong, ZHU Xi, JIAN Lin-an,et al. Acoustic stealth design on the underwater sandwich composite added structure for oblique incidence[J]. Journal of Vibration and Shock, 2009, 28(5): 49-54.
[ 4 ] 王曼. 水声吸声覆盖层理论与实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2004.
[ 5 ] Gaunaurd G. Comments on absorption mechanisms for water borne sound in Alberich anechoic layers[J]. Ultrasonic, 1985, 23(2): 90-91.
[ 6 ] Lee Y Y, Lee E W M,Ng C F. Sound absorption of a finite flexible micro-perforated panel backed by an cavity[J]. Journal of Sound and Vibration, 2005, 287(1-2): 227-243.
[ 7 ] Sakagami K, Morimoto M, Koike W. A numerical study of double-leaf microperforated panel absorbers[J]. Applied Acoustics, 2006, 67(7): 609-619.
[ 8 ] 何世平, 汤渭霖,何琳,等. 变截面圆柱形空腔覆盖层吸声系数的二维近似解[J]. 船舶力学, 2006, 10(1): 120-127. HE Shi-ping, TANG Wei-lin,HE Lin,et al. Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity[J]. Journal of Ship Mechanics, 2006, 10(1): 120-127.
[ 9 ] 朱蓓丽, 任克明. 等效参数法研究带圆柱通道橡胶体的声学性能[J]. 上海交通大学学报,1997,31(7):20-25. ZHU Bei-li, REN Ke-ming. Analysis of acoustics properties of rubber with column cavity with equivalent parameters[J]. Journal of Shanghai Jiaotong University, 1997, 31(7): 20-25.
[10] Mead D J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling[J]. Journal of Sound and Vibration, 1973, 27(2): 235-260.
[11] Hladky-Hennion A C, Decarpigny J N. Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method: application to Alberich anechoic coatings[J]. Journal of Acoustic Society of America, 1991, 90(6):3356-3367.
Tests for acoustic-stealth characteristics of underwater sandwich composite structures with cava
LUO Zhong1,ZHOU Xin2
(1. Department of Researching, Naval Univ. of Engineering, Wuhan 430033, China;2. Naval Deputation Department in Shanghai, Shanghai 201206, China)
Introducing cava can improve the sound-absorption ability of a sandwich composite structure within a low-frequency range. The acoustic models for 3 kinds of typical underwater acoustic-stealth structures were established. The affect factors of their sound-absorption ability were analyzed numerically. Then, using the test method of pulse sound tube, the effects of samples with cava or without cava, different distances between cava, shape and depth of cava on the peak value of sound-absorption resonance and its frequency of the structures were analyzed under hard boundary condition and air background as well as soft boundary condition and water background. The results showed that the cava obviously improve the sound-absorption ability of sandwich composite structures within a low-frequency range; under air background, the smaller the distance between cava, the larger the peak value of the 1storder sound-absorption resonance and the lower the corresponding frequency; under water background, the situation is the opposite; the bigger the volume of cava, the smaller the peak value of the 1storder sound-absorption resonance and the lower the corresponding frequency.
sandwich composite structure; cavum; absorption coefficient; resonance; experiment
国防重点基金资助项目
2013-07-16 修改稿收到日期:2013-11-28
罗忠 男,讲师,博士,1982年生
TN911.7
A
10.13465/j.cnki.jvs.2014.08.022
