脉动风速过程模拟的正交展开-随机函数方法

刘章军， 万 勇， 曾 波

(三峡大学 土木与建筑学院，湖北 宜昌 443002)

脉动风速过程模拟的正交展开-随机函数方法

刘章军， 万 勇， 曾 波

(三峡大学 土木与建筑学院，湖北 宜昌 443002)

在随机过程的正交展开基础上，采用随机函数的思想，提出了脉动风速随机过程模拟的正交展开-随机函数方法。通过将展开式中的一组标准正交随机变量表达为基本随机变量的正交函数形式，实现了用一个基本随机变量来表达原随机过程的目的。应用正交展开-随机函数方法，对脉动风速随机过程进行模拟分析。结果表明，在二阶数值统计意义上，仅需用一个基本随机变量即可对脉动风速随机过程进行精确模拟，进而体现了正交展开-随机函数方法的有效性和优越性。

脉动风速；模拟；正交展开；随机函数；高斯过程；非高斯过程

在风工程中，脉动风通常可近似认为是一个各态历经、零均值的平稳随机过程。对于高耸结构、高层建筑结构和大跨度桥梁结构等，脉动风对结构的动力效应显著，是结构设计时所需考虑的一类重要随机动力荷载[1]。

目前，模拟脉动风过程的方法有多种[2]，主要包括谐波合成法及其改进方法[3-4]、线性滤波法、本征正交分解法[5-7]、小波分析法以及混合法[8-9]等，这些方法主要是针对平稳高斯随机过程进行模拟。此外，李锦华等[10]进行了非平稳脉动风速的数值模拟，孙芳锦等[11]进行了非高斯风场的数值模拟研究。Li等[12]从大气湍流的物理图景出发，结合具体物理参数的建模，建立了具有物理基础的脉动风速随机Fourier幅值谱模型。文献[13]建立了一般随机过程的正交展开理论，文献[14]进行了脉动风速随机过程的正交展开研究。在此基础上，本文试图采用文献[15]中提出的随机函数思想，结合正交展开方法，对脉动风速随机过程进行正交展开-随机函数的模拟研究，以求用一个基本随机变量即可在二阶数值统计意义上对脉动风速随机过程进行精确地模拟，并能获得具有给定概率的样本函数。进一步地，研究基于互功率谱密度函数或基于功率谱密度函数矩阵的随机风场概率模型，并结合近年来发展起来的概率密度演化理论[16-17]，为工程结构精细化的抗风动力响应分析及动力可靠度研究提供基础。

1 随机过程的正交展开-随机函数方法

1.1 随机过程的正交展开

(1)

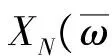
在式(1)中，λj与Фj分别为相关矩阵R的特征值和标准正交特征向量：

RФj=λjФj

(2)

注意，式(1)中φjk即为标准正交特征向量Фj的第k行元素，即

Фj={φj1,φj2,…,φjN}T

在式(2)中，相关矩阵R=[ρij]N×N可按下式来得到[13]：

(i,j=1,2,…,N)

(3)

(4)

文献[9]给出的误差限值ε≤0.10，为提高精度，本文认为脉动风速过程的均方相对误差应不超过5%，即ε≤0.05。

需要指出的是，在正交展开式(1)中，特征值λj与相应的特征向量Фj应按特征值的大小依次降次排列。

1.2 标准正交随机变量的随机函数表达

(5)

其中，E[·]表示数学期望，δij为Kronecker记号。

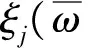
(6)

其中， pΘ(θ)为基本随机变量Θ的概率密度函数。

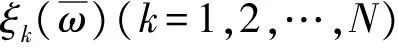
1.2.1 非高斯随机变量的构造

(1) 选取定义在区间[-1,1]上的Legendre正交多项式[15]：

k=1,2,…,N

(7)

其中Pn(x)为Legendre多项式，其递推公式为

(8)

(2) 选取定义在区间[-π,π]上的Hartley正交基函数[15]：

(8)

1.2.2 高斯随机变量的构造

Fξk(x)=

(10)

利用随机变量的等概率反变换法，即可获得一组具有标准高斯分布的正交随机变量[15]：

(11)

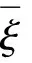
2 脉动风速过程的模拟

2.1Davenport脉动风速谱及其等价功率谱

在上述随机过程的正交展开-随机函数方法中，需要由随机过程的自相关函数来计算正交展开式(1)中的特征值λj和标准特征向量Φj。因此，首先需要根据脉动风速的功率谱密度函数求出相应的自相关函数。

在风工程中，Davenport提出了与高度无关的脉动风速功率谱密度函数，即Davenport谱(单边谱)[18]：

(12)

考虑到直接由Davenport谱来计算自相关函数的表达式比较困难，文献[14]给出了Davenport谱的等价功率谱密度函数(双边谱)：

(13)

其中，参数A、α及β可由功率谱的面积、卓越频率及峰值均相等的等价原则来确定。

根据Davenport谱与其等价功率谱的等价条件，可知：

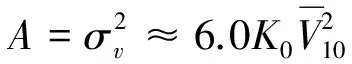
(14)

(15)

2.2 实例分析与验证

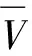
表1 基本随机变量的离散点集

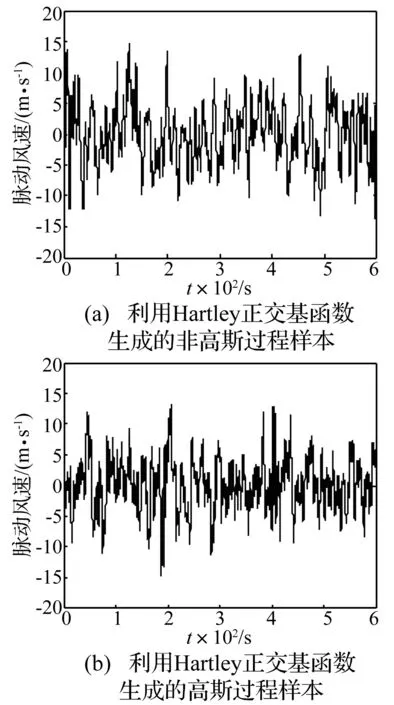
图1 脉动风速的典型样本时程曲线Fig.1 Generated samples for fluctuating wind

图2给出了由Legendre正交多项式(7)所生成1 600条脉动风速样本函数的二阶统计特性与目标特性的比较，从图中可知，样本总体均值、标准差与目标均值、标准差以及样本总体功率谱与目标功率谱均符合较好。图3给出了利用Hartley正交基函数(即式(9))所生成628条非高斯脉动风速样本的总体均值、标准差以及总体功率谱与目标均值、标准差和目标功率谱的比较，可见其符合程度十分理想。图4给出了利用式(11)所生成628条高斯脉动风速样本的总体均值、标准差以及总体功率谱与目标均值、标准差和目标功率谱的比较，从图中可知，它们之间的符合程度也很理想。

图2 利用Legendre正交多项式生成1600条脉动风速样本的统计特性与目标特性比较Fig．2Comparisonthetargetsandsecond⁃orderstatisticsof1600non⁃Gaussianprocess’ssamplesgeneratedusingLegendreorthogonalpolynomials图3 628条非高斯脉动风速样本函数的统计特性与目标特性比较Fig．3Comparisonthetargetsandsecond⁃orderstatisticsof628generatednon⁃Gaussianprocess’ssamples图4 628条高斯脉动风速样本函数的统计特性与目标特性比较Fig．4Comparisonthetargetsandsecond⁃orderstatisticsof628generatedGaussianprocess’ssamples

在图2～图4样本总体功率谱的图形中，当频率在0.82 Hz以上范围时，样本总体的功率谱密度函数为零，这是由于在脉动风速过程的近似正交展开式(1)中，展开项数N=1 000而不是趋于无穷大所致。这表明，当展开项数N越大时，两者的高频段部分将会符合得越理想。

顺便指出，与文献[15]中平稳地震动过程的正交展开-随机函数模拟的结果相比，脉动风速过程的模拟结果更为理想。脉动风速过程对于三种标准正交随机变量的随机函数构造，其模拟效果均比较理想，而地震动过程对于Legendre正交多项式和高斯随机变量构造的模拟效果稍欠佳，其可能原因是脉动风速过程的持续时间为600 s，比地震动过程的持续时间20 s更长，更能符合平稳随机过程的假定，因而对随机函数构造的选择没有地震动过程那么敏感。这表明，平稳随机过程的正交展开-随机函数方法具有良好的适用性和稳定性。

3 结 论

在随机过程的正交展开基础上，通过将展开式中的一组标准正交随机变量表达为基本随机变量的正交函数形式，实现了用一个基本随机变量来表达原随机过程的目的。文中以Davenport脉动风速谱及其等价功率谱为例，通过标准正交随机变量的Legendre正交多项式和Hartley基函数形式的构造，对脉动风速非高斯平稳过程和高斯平稳过程进行了模拟。结果表明，本文方法所需基本随机变量的数量最少，且模拟的精度很高，同时可以对高斯平稳过程和非高斯平稳过程进行模拟，进而体现了正交展开-随机函数方法的有效性和优越性。此外，利用本文随机函数的思想，可以进一步研究基于互功率谱密度函数或者基于功率谱密度函数矩阵的风速随机场模拟。

[ 1 ] 李杰, 刘章军. 随机脉动风场的正交展开方法[J]. 土木工程学报, 2008, 41(2): 49-53. LI Jie, LIU Zhang-jun. Orthogonal expansion method of random fields of wind velocity fluctuations[J]. China Civil Engineering Journal, 2008, 41(2): 49-53.

[ 2 ] 李锦华, 李春祥. 土木工程随机风场数值模拟研究的进展[J]. 振动与冲击, 2008, 27(9): 116-125. LI Jin-hua, LI Chun-xiang. Development of numerical simulations for stochastic wind fields in civil engineering[J]. Journal of Vibration and Shock, 2008, 27(9): 116-125.

[ 3 ] Deodatis G. Simulation of ergodic multivariate stochastic processes [J]. Journal of Engineering Mechanics, 1996, 122(8): 778-787.

[ 4 ] Cao Y H, Xiang H F, Zhou Y. Simulation of stochastic wind velocity field on long-span bridges[J]. Journal of Engineering Mechanics, 2000, 126(1): 1-6.

[ 5 ] Chen X Z, Kareem A. Proper orthogonal decomposition-based modeling, analysis, and simulation of dynamic wind load effects on structures[J]. Journal of Engineering Mechanics, 2005, 131(4): 325-339.

[ 6 ] Di Paola M. Digital simulation of wind field velocity [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 91-109.

[ 7 ] Carassale L, Solari G. Wind modes for structural dynamics: a continuous approach [J]. Probabilistic Engineering Mechanics, 2002, 17(2): 157-166.

[ 8 ] 胡亮, 顾明, 李黎. 基于本征正交分解的谱表示法模拟风场的误差[J]. 振动与冲击, 2011, 30(4): 12-15. HU Liang, GU Ming, LI Li. Errors produced with proper orthogonal decomposition-based spectral representation method in wind velocity field simulation [J]. Journal of Vibration and Shock, 2011, 30(4): 12-15.

[ 9 ] Chen L Z, Letchford C W. Simulation of multivariate stationary Gaussian stochastic processes: Hybrid spectral representation and proper orthogonal decomposition approach [J]. Journal of Engineering Mechanics, 2005, 131(8): 801-808.

[10] 李锦华, 李春祥, 申建红. 非平稳脉动风速的数值模拟[J]. 振动与冲击, 2009, 28(1): 18-23. LI Jin-hua, LI Chun-xiang, SHEN Jian-hong. Numerical simulation of non-stationary fluctuating wind velocity[J]. Journal of Vibration and Shock, 2009, 28(1): 18-23.

[11] 孙芳锦, 张爱社. 基于谱修正方法的非高斯风场模拟[J]. 防灾减灾工程学报, 2012, 32(2): 187-190. SUN Fang-jin, ZHANG Ai-she. Non-Gaussian wind field simulation based on spectral correction method[J]. Journal of Disaster Prevention and Mitigation Engineering, 2012, 32(2): 187-190.

[12] LI Jie, PENG Yong-bo, YAN Qi. Modeling and simulation of fluctuating wind speeds using evolutionary phase spectrum [J]. Probabilistic Engineering Mechanics, 2013, 32: 48-55.

[13] 李杰, 刘章军. 基于标准正交基的随机过程展开法[J]. 同济大学学报(自然科学版), 2006, 34(10): 1279-1283. LI Jie, LIU Zhang-jun. Expansion method of stochastic processes based on normalized orthogonal bases [J]. Journal of Tongji University (Natural Science), 2006, 34(10): 1279-1283.

[14] 刘章军, 李杰. 脉动风速随机过程的正交展开[J]. 振动工程学报, 2008, 21(1): 96-101. LIU Zhang-jun, LI Jie. Orthogonal expansion of stochastic processes for wind velocity[J]. Journal of Vibration Engineering, 2008, 21(1): 96-101.

[15] 刘章军, 万勇, 镇斌. 平稳地震动过程的正交展开-随机函数模型[J]. 应用基础与工程科学学报, 2014, 22(2).

[16] LI Jie, CHEN Jian-bing. Stochastic dynamics of structures [M]. Singapore: John Wiley & Sons Pte Ltd, 2009.

[17] 李杰, 陈建兵. 随机动力系统中的概率密度演化方程及其研究进展[J]. 力学进展, 2010, 40(2): 170-188. LI Jie, CHEN Jian-bing. Advances in the research on probability density evolution equations of stochastic dynamical systems [J]. Advances in Mechanics, 2010, 40(2): 170-188.

[18] Davenport A G. The spectrum of horizontal gustiness near the ground in high winds [J]. Q. J. R. Meteorol. Soc., 1961, 87(372): 194-211.

Simulation of fluctuating wind processes with an orthogonal expansion-random function approach

LIU Zhang-jun, WAN Yong, ZENG Bo

(College of Civil Engineering & Architecture, Three Gorges University, Yichang 443002, China)

Based on the orthogonal expansion of stochastic processes, and the idea of random function, a hybrid orthogonal expansion-random function approach was proposed to simulate fluctuating wind. With this method, the standard orthogonal random variables in an orthogonal expansion formula were expressed into the orthogonal function form of a basic random variable to realize applying a basic random variable to express an original stochastic process. Utilizing the proposed approach, the simulation of fluctuating wind processes was perfomed. The results showed that the proposed approach can be used to accurately simulate the second-order statistics of fluctuating wind processes with only a basic random variable; the effectiveness and advantages of the orthogonal expansion-random function method are verified.

fluctuating wind; simulation; orthogonal expansion; stochastic function; Gaussian stationary process; non-Gaussian stationary process

国家自然科学基金资助项目(51278282, 50808113)；三峡地区地质灾害与生态环境湖北省协同创新中心

2013-10-09 修改稿收到日期：2013-11-21

刘章军 男，博士，教授，1973年生

O324；TU311.3

A

10.13465/j.cnki.jvs.2014.08.021