钢筋混凝土框架-核心筒结构地震反应能量分析

李 坤， 史庆轩, 王 朋， 王 南， 王秋伟

(1. 西安建筑科技大学 土木工程学院，西安 710055；2.东营市 城市规划局 山东 东营 257000)

钢筋混凝土框架-核心筒结构地震反应能量分析

李 坤1,2， 史庆轩1, 王 朋1， 王 南1， 王秋伟1

(1. 西安建筑科技大学 土木工程学院，西安 710055；2.东营市 城市规划局 山东 东营 257000)

通过对9个不同结构特性的钢筋混凝土框架-核心筒结构，选用一定数量的地震波进行时程分析，研究了此类结构在地震作用下的总输入能及其在滞回耗能和阻尼耗能之间的分配规律，以及滞回耗能在构件及层间的分布规律。研究表明，随着地震动幅值的增大，滞回耗能比也随之增加；不同频谱特性的地震波对滞回耗能影响较大；刚度特征值对结构总滞回耗能影响不大，但对构件的耗能分配具有较大影响；结构滞回耗能主要集中于底层剪力墙和中部连梁处。

钢筋混凝土框架核心筒；能量反应；滞回耗能；结构特性

地震对结构的作用从本质上来说是一种能量的传递、转化和消耗过程。近年来，基于能量的抗震设计方法[1]受到国内外工程界的广泛关注。相对于基于承载力和基于位移的抗震设计，基于能量抗震设计思想更加注重从结构的损伤模式和耗能机制控制[2]入手，实现对结构耗能分布的控制，这使得基于能量抗震设计能更好的从整体上把握结构的抗震性能。从能量角度来分析结构的动力反应，能较好的认识结构在强震下的非线性性能及评价破坏程度[3-4]。在基于能量抗震设计中，对于各能量项的定义及能量分配是首先要解决的问题。

钢筋混凝土框架-核心筒结构是高层建筑结构中应用较多的结构形式之一。结构由核心筒墙肢、连梁、框架等构件形成多道抗震防线，结构中各构件的耗能分布相差较大，同时，结构沿高度方向的能量分布也较复杂，针对此类结构国内外研究较少[5]。本文选取典型钢筋混凝土框架-核心筒计算模型，依照地震波选取原则[6]，采用弹塑性时程分析方法，研究了结构在不同地震动下的能量分配规律，以及总滞回耗能在各构件中沿结构高度的能量分配及其影响因素。

1 能量计算方法

1.1 多自由度体系能量反应方程

多自由度结构在水平地震作用下的振动方程：

(1)

EK+ED+EF=EI

(2)

式中：EK分别为结构的动能、ED阻尼耗能、EF变形能；EI为地震输入能。其中，结构变形能可分为弹性应变能ES和滞回耗能EH，在结构地震能量反应时程中，结构动能与弹性应变能相互转化，并在振动结束时都趋近于零，因此，从能量方程平衡的角度来说，对于弹性体系，地震输入的能量EI将由阻尼耗能ED全部耗散；对于弹塑性体系，地震输入的能量将由累积滞回耗能EH和阻尼耗能ED两部分来共同耗散。

1.2 滞回耗能和阻尼耗能

结构能否有效抵抗地震作用，将取决于其累积滞回耗能和阻尼耗能能力是否大于地震输入能量。EH将导致结构破坏，产生累积损伤，从结构设计的角度来说，累积滞回耗能的需求和实际耗能能力更值得关注。结构的累积损伤与滞回耗能直接相关，总输入能一定时，结构的破环程度可通过滞回耗能所占比重来反映；同时，滞回耗能在结构各构件中的分配也可以反映结构在地震作用下的耗能机制是否合理。

阻尼耗能是反映结构体系振动过程中能量耗散的重要参数，对于降低结构在地震作用下的损伤具有重要作用。在多自由度体系中，通常采用等效粘滞阻尼模型，其中Rayleigh阻尼模型物理意义明确、计算方便，得到了最为广泛的应用。Rayleigh阻尼假设阻尼矩阵与刚度矩阵和(或)质量矩阵成比例，即：

[C]=a[M]+b[K]

(3)

其中，a[M]阻尼器连接质量和大地，它贡献外部阻尼力；b[K]阻尼器和结构单元并联，它贡献内部阻尼力。根据振型正交条件，系数a、b可以通过常数阻尼比和模态周期来确定：

(4)

式中，ωk为结构圆频率。本文结构阻尼采用瑞利阻尼，阻尼比为0.05。

2 结构分析模型及地震波的选取

2.1 结构分析模型

为了更清晰地揭示钢筋混凝土框架-核心筒结构的能量分布规律，同时使参数化分析更具有一般规律性，本文选取计算模型以规则结构为原则，结构水平方向布置对称，竖向无刚度突变，并根据我国《抗震规范》[7]采用PKPM软件进行设计一个30层钢筋混凝土框架-核心筒结构，结构标准层平面如图1所示。设计地震烈度为8°，1 -10层混凝土等级为C50，11-25层为C45，26-30层为C40。剪力墙、连梁分布钢筋采用HPB300级，框架梁、柱采用HRB335级。剪力墙水平配筋率为0.85%，竖向配筋率为1.2%。同时，为了研究不同结构动力特性对结构滞回耗能分布的影响，在原计算模型的基础上改变连梁跨高比、剪力墙厚度及框架柱截面尺寸等因素，设计了8个对比模型，表1为9种结构类型设计信息。经计算，结构在8度小震和大震作用下结构层间位移角最大值分别为1/817和1/206，均满足规范要求。

图1 结构标准层平面图Fig.1 Plan of structural standard floor

结构类型层数连梁高度/mm剪力墙厚度/mm框架柱/mm刚度特征值18001．35210006001．2331200900×9001．414305001．4554001．5961000750×7501．237600600×6001．01825750×7501．139200．9

2.2 计算模型的建立

本文采用基于纤维模型的非线性分析软件PERFORM-3D对上述结构模型进行动力弹塑性分析。钢筋应力-应变曲线采用无下降段的二折线模型，混凝土应力-应变关系采用Mander模型[8]。剪力墙计算模型采用非线性剪力墙纤维单元并添加非弹性剪切材料，以纤维单元模拟剪力墙平面内弯曲-轴力特性，非线性剪切材料模拟平面内剪切效应，平面外弯曲、平面外剪切及扭转效应均采用弹性本构模拟。连梁计算模型采用梁单元并添加纤维截面及剪切铰的方式进行模拟，埋设梁贯通墙截面，以纤维截面模拟连梁弯曲-轴力特性，剪切铰模拟连梁剪切效应。对于框架梁和框架柱的模拟比较类似，首先建立由两端设置塑性区和中间弹塑性或弹性杆组成的梁和柱构件单元，然后分别以纤维截面定义相对于梁或柱的塑性区，塑性区长度取为0. 5h,h为梁或柱的截面高度，为了考虑构件的P-Δ效应，分别沿水平方向和高度方向将梁和柱划分为3个单元，并定义其局部坐标。

2.3 地震记录的选择

时程分析过程中，地震记录的选择对计算结果影响较大，结构在不同地震动作用下的地震反应随地震动的峰值、频谱和持时而改变，从而造成计算结果的离散性较大，因此地震动的输入应遵循一定的原则。本文根据文献[6]中建议的选波原则，在美国太平洋地震研究中心的数据库及中国地震台网中选择了11条地震波，表2列出这11条地震记录的相关参数信息。计算时将峰值加速度调整为0.2 gal、0.4 gal、0.6 gal、0.8 gal。本文采用强震持时[9]td的概念定义地震动持时：

td=t0.95-t0.05

(5)

式中，t0.95和t0.05分别为地震动Arias强度IA为5%和95%时的时间间隔，地震动Arias强度IA表达式为

(6)

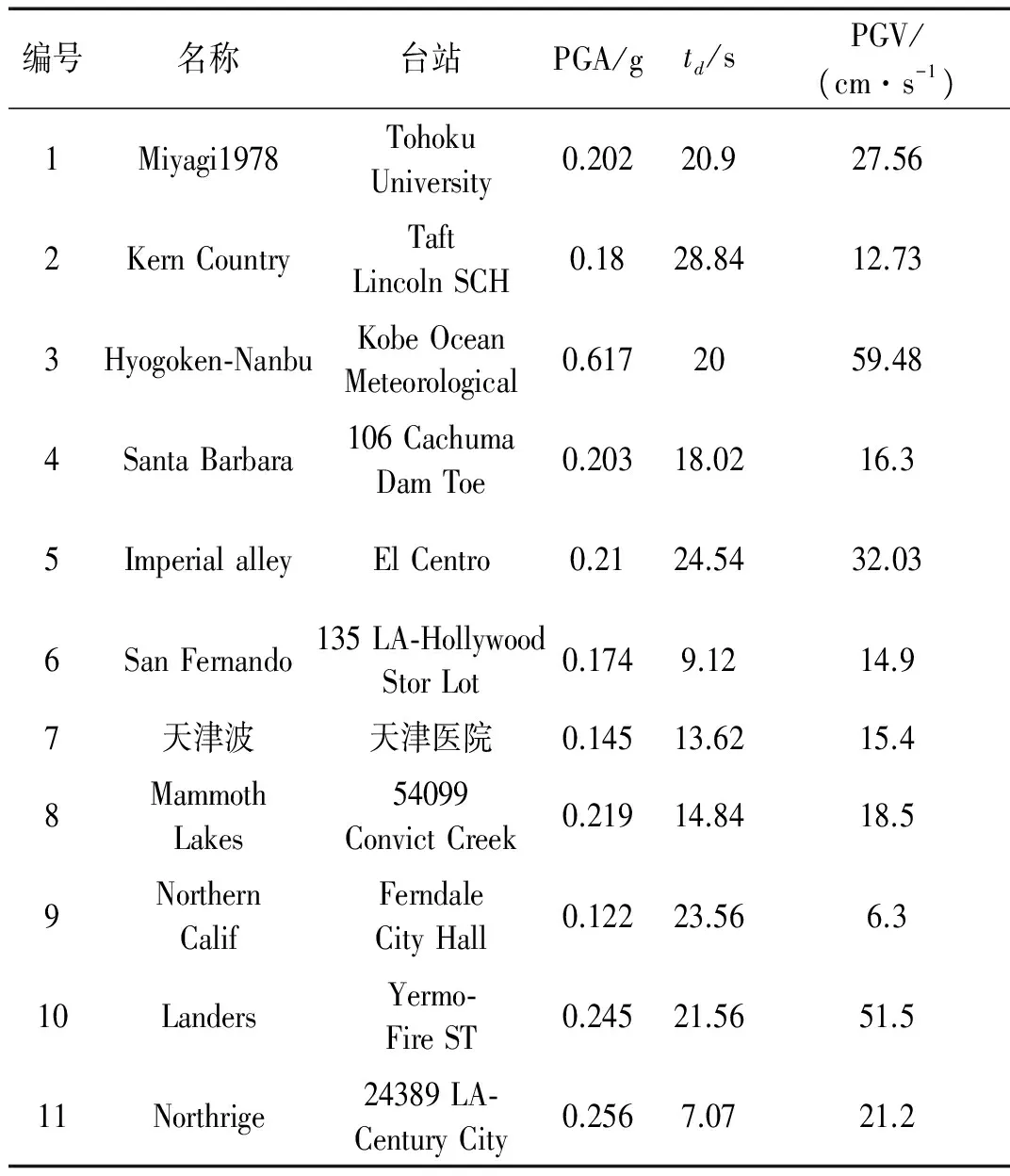
表2 强震记录及地震动参数

3 能量分布规律

3.1 结构地震总耗能及能量分配

表3和图3为结构1在各条地震波对应8度小震和大震作用下的总输入能及能量分配情况。可以看出，结构在不同地震波作用下总输入能虽然相差较大，但总输入能在各能量项中的分配比例差别不大。结构动能及弹性应变能所占比例很小，主要依靠阻尼耗能及滞回耗能抵抗地震输入能量，占到总输入能的80%左右。11条地震波小震作用下，结构阻尼耗能平均占总输入能的65%，滞回耗能平均占14%；大震作用下，结构阻尼耗能平均占总输入能的50%，滞回耗能平均占38%。

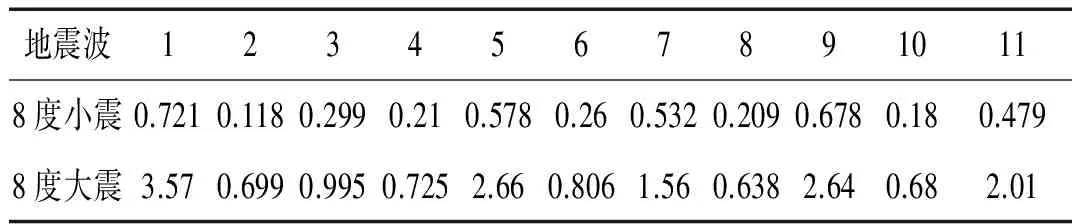
表3 地震作用下总输入能统计结果(×1010 N·mm)

图3 地震作用下各能量项耗能比例Fig.3 Energy ratio of structure lunder all ground motions

3.2 结构总滞回耗能

图4给出了结构1在不同加速度峰值下滞回耗能变化情况。由图4可知，在不同的地震波作用下，随着加速度峰值增大，滞回耗能比的发展趋势基本一致，可以分为两个阶段。当加速度峰值在0.2 gal到0.6 gal之间时，滞回耗能比迅速增大，增大幅度在2.8～3.5倍之间。说明在此阶段，塑性变形迅速增加，结构通过各构件的损伤抵抗地震输入能量。当加速度峰值达到0.6 gal后，结构塑性发展幅度减小，同时结构破坏引起阻尼比的增大，阻尼耗能在总耗能中比例上升，使得滞回耗能比增大幅度减小。

9个结构模型通过增大或减小连梁、剪力墙墙厚和框架柱截面尺寸来改变刚度特征值，图5为9个结构在8度罕遇地震作用下刚度特征值的变化对滞回耗能比的影响。由图5可知，随着刚度特征值的增大，结构滞回耗能比虽有小幅下降，但幅度不大，甚至有的结构呈上升趋势，这说明刚度特征值的变化对于整个结构的滞回耗能比影响不大。结构在8度罕遇地震作用下滞回耗能比均匀分布在0.3到0.65之间。

已有研究表明，地震动卓越周期与结构基本周期越接近，结构地震反应越剧烈。图6为8度罕遇地震作用下，9个结构基本周期与地震动卓越周期之比的变化对结构滞回耗能比的影响。定义结构基本自振周期与地震动卓越周期之比为ξ。

由图6可以看出，ξ值对结构滞回耗能影响较大。ξ值越大，说明结构基本周期与地震动卓越周期相差越大。ξ值在2～6之间时，随着ξ值增大，结构滞回耗能比随之降低，且下降幅度较大；当ξ>6时，结构滞回耗能比虽也随之降低，但幅度明显减缓。这说明结构自振周期与地震动卓越周期相差不大时，ξ值与结构滞回耗能比相关性较好。当结构自振周期与地震动卓越周期相差较大时，ξ值对结构滞回耗能比的影响基本可以忽略。

图4 不同加速度峰值下滞回耗能比例Fig．4EH/EIunderdifferentseismicpeak图5 刚度特征值与滞回耗能比关系Fig．5RelationshipbetweeneigenvalueofstiffnessandEH/EI图6 ξ与滞回耗能比的关系Fig．6RelationshipbetweenξandEH/EI

3.3 滞回耗能在各类构件之间的分配

仅依靠滞回耗能或滞回耗能比无法准确反映结构特别是典型构件的塑性发展情况，因此，必须深入研究构件耗能分配，了解结构的耗能机制，从而综合判定结构抗震性能。图7为结构1在8度小震下构件滞回耗能分配情况。由图可以看出，在小震下剪力墙耗能平均占总滞回耗能的58%，是主要耗能构件。连梁、框架梁比例较小，分别为28.6%、12.7%，框架柱保持弹性，不参与耗能。分析原因，在小震作用下，结构基本处于弹性状态，连梁塑性发展不充分，主要依靠底层墙肢塑性变形来抵抗地震能量输入。

图8为大震下作用下构件耗能比，连梁是主要耗能构件，平均占总滞回耗能的62.7%，剪力墙墙肢、框架梁和框架柱耗能分别为24.7%、12.5%，7.6%。分析原因，在罕遇地震作用下，结构位移加大，结构中上部连梁参与塑性耗能程度加大，而剪力墙上部塑性发展程度较轻，甚至保持弹性。可以看出，在钢筋混凝土框架-核心筒结构中，连梁和剪力墙是结构抵抗地震作用的第一道防线，外框架为第二道防线。

图9为9个结构在taft波8度罕遇地震作用下各构件耗能随刚度特征值变化情况。由图可以看出，刚度特征值对于连梁耗能影响较小，对于剪力墙和框架梁、框架柱耗能影响较大。随着刚度特征值的增大，剪力墙耗能占总滞回耗能比值由37%下降到20%，而框架梁和框架柱耗能分别由9%和6%上升到19%和15% ，且基本呈线性分布。这是因为当刚度特征值增大时，框架与剪力墙刚度比增大，地震作用下所承担的剪力也相应增大，框架所耗能比值随之线性增加，而剪力墙耗能比例随之降低。这说明在剪力分担率符合规范要求的前提下，适当增加外框架刚度可以有效降低内部核心筒的损伤。

3.4 滞回耗能层间分配规律

图10、图11分别为Taft波作用下结构1在罕遇地震作用下剪力墙及连梁滞回耗能沿高度的耗能分配规律。图12为相应地震波作用下结构层间位移角和受力层间位移角沿高度变化情况。受力层间位移角根据《广东省实施<高层建筑混凝土结构技术规程>(JGJ3-2002)补充规定》第3.5.1条规定：对于弯曲型结构受力层间位移:

(7)

由图可知，剪力墙滞回耗能沿高度增加而逐渐减小，底层剪力墙耗能占剪力墙总滞回耗能的比值最大，为53.8%；结构中部连梁耗能较多，结构第20层连梁耗能占总连梁耗能比值最大，底部及上部连梁耗能较少。说明在罕遇地震作用下，结构主要依靠底层墙肢及中部连梁变形损伤抵抗地震输入能量。对比图12，剪力墙耗能沿高度分配规律与结构受力层间位移相关性较好，受力位移越大，墙肢耗能越多；连梁耗能分配规律与结构层间位移变化一致，层间位移角越大，连梁变形越大，破坏越严重，连梁耗能也较多。

图7 结构1在小震作用下各构件耗能比例Fig．7Distributionofdissipatedenergybydifferentmembersinstructure1underminorearthquake图8 结构1在大震作用下各构件耗能比例Fig．8Distributionofdissipatedenergybydifferentmembersinstructure1underrareearthquake图9 结构1刚度特征值与滞回耗能比关系Fig．9RelationshipbetweeneigenvalueofstiffnessandEH/EI

图10 结构1剪力墙耗能分布规律Fig．10DistributionofEHbyshearwallsalongthestoriesinstructure1图11 结构1连梁耗能沿高度分配规律Fig．11DistributionofEHbycoupling⁃beamalongthestoriesinstructure1图12 框架-核心筒结构层间位移角Fig．12Storydriftangleofreinforcedconcreteframe⁃corewall

4 结 论

(1) 结构在不同地震波作用下总输入能虽然有所差别，但总输入能在各能量项中的分配比例差别不大。随着地震动幅值的增大，滞回耗能比也随之增加，当地震动幅值增大到一定程度时，结构滞回耗能便不再增大。

(2) 结构自振周期与地震动卓越周期比值ξ较小时，ξ值与结构滞回耗能比相关性较好。ξ值较大时，ξ值对结构滞回耗能比的影响基本可以忽略。刚度特征值对结构总滞回耗能影响不大，但对构件的耗能分配具有较大影响。刚度特征值增大，框架所耗能比值随之线性增加，而剪力墙耗能比例随之降低。

(3) 结构主要依靠底层墙肢及中部连梁变形损伤抵抗地震输入能量。剪力墙耗能沿高度分配规律与结构受力层间位移相关性较好，受力位移越大，墙肢耗能越多；连梁耗能分配规律与结构层间位移变化一致，层间位移角大处连梁耗能较多。

[1] Housner G W. Behavior of structures during earthquake [J]. Journal of the Engineering Mechanics Division, ASCE, 1959, 85(4): 109-129.

[2] 肖明葵, 刘纲, 白绍良,等. 抗震结构的滞回耗能谱[J]. 世界地震工程, 2002, 18(3): 110-115. XIAO Ming-kui, LIU Gang, BAI Shao-liang，et al. The hysteretic energy spectya of seismic structures[J]. World Earthquake Engineering, 2002, 18(3): 110-115.

[3] Park Y J, Ang A S, Wen Y K. Seismic damage analysis of reinforced concrete buildings [J]. Journal of Structural Engineering, ASCE, 1985, 111(4): 740-757.

[4] Kunnath S K, Chai Y H. Cumulative damage-based inelastic cyclic demand spectrum [J]. Earthquake Engineering & Structural Dynamics, 2004, 33(4): 499-520.

[5] 尧国皇, 王卫华, 郭明.超高层钢框架-钢筋混凝土核心筒结构的弹塑性时程分析[J].振动与冲击, 2012, 31 (14):137-142. YAO Guo-huang,WANG Wei-hua,Guo Ming.Elastic-plastic time history analysis on super rise steel frame-core wall structure [J]. Journal of Vibration and Shock, 2012, 31 (14):137-142.

[6] 杨溥, 李英民, 赖明. 结构时程分析法输入地震波的选择控制指标[J]. 土木工程学报, 2000, 33(6): 33-37. YANG Pu, LI Ying-min, LAI Ming. A new method for selecting inputting waves for time-history analysis [J]. China Civil Engineering Journal, 2000, 33(6): 33-37.

[7] 中华人民共和国建设部. GB50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[8] Mander J B, Priestley M J N, Park R. Theoretical stress strain model for confined concrete [J]. Journal of Structure Engineering, ASCE, 1988, 114(8): 1804-1826.

[9] Trifunac M D, Brady A G.A study on the duration of strong earthquake ground motion [J]. Bulletin of Seismological Society of America, 1975, 65 (3):581-626.

Seismic response energy analysis for reinforced concrete frame-core wall structures

LI Kun1，2, SHI Qing-xuan1, WANG Peng1, WANG Nan1, WANG Qiu-wei1

(1.School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055,China;2. Uvben and Rural Planning Bureau of Dongyin City, Dongyin 257000, China)

Elastio-plastic dynamic analyses of 9 reinforced concrete frame-core wall structures with different structural characteristics were performed under several sets of ground motions. The earthquake total input energy of the structure under ground motion, and the distribution regularity of the total input energy between hysteretic energy-dissipation and damping energy-dissspation were studied. The distribution of hysteretic energy-dissipation among shear wall, coupled beams and frames, and the distribution of hysteretic energy-dissipation along different stories were analyzed. The results showed that the hysteretic energy-dissipation increases with increase in the peak ground acceleration; the earthquake records with different spectral characteristics have a great influence on hysteretic energy-dissipation; although the total hysteretic energy-dissipation of structural members are steady, the distribution of hysteretic energy-dissipation among shear wall, coupled beams and frames depends on the structural stiffness features; the structural hysteretic energy-dissipation is concentrated in the bottom portion of shear walls and the middle part of coupled beams.

reinforced concrete frame-core wall structure; energy response; hysteretic energy-dissipation; structural characteristics

国家自然科学基金项目(51178380,51108370)

2012-11-19 修改稿收到日期：2013-05-03

李坤 男，博士生，1983年11月生

TU355

A

10.13465/j.cnki.jvs.2014.08.020