基于离心力和陀螺力矩效应的“主轴-轴承”系统动力学特性研究

胡 腾， 殷国富， 孙明楠

(四川大学 制造科学与工程学院,成都 610065)

基于离心力和陀螺力矩效应的“主轴-轴承”系统动力学特性研究

胡 腾， 殷国富， 孙明楠

(四川大学 制造科学与工程学院,成都 610065)

研究“主轴-轴承”系统在高转速场中受离心力和陀螺力矩影响的动力学特性对于提高主轴系统运行稳定性有重要的作用。在扩展Harris滚动轴承非线性分析模型、建立滚动轴承耦合刚度矩阵的基础上，建立了一种综合考虑主轴离心力效应和陀螺力矩效应的“主轴-轴承”系统动力学数字模型，并借助锤击模态实验验证了其准确性；分析论述了主轴离心力效应、主轴陀螺力矩效应及滚动轴承运行刚度对“主轴-轴承”系统在高转速场中的动力学特性的影响规律。通过模型分析计算表明：当轴承处于超轻预紧(EL)工况时，主轴的高速效应比轴承运行刚度对“主轴-轴承”系统动力学特性的影响更大，尤以主轴陀螺力矩效应的影响最为突出。

高转速场；“主轴-轴承”系统；动力学特性；离心力；陀螺力矩；运行刚度

近年来在我国航空航天、军工、汽车、能源等行业领域，为不断提高加工效率，高速加工技术发展十分迅速。高速主轴单元作为高速加工技术的主要载体，其动力学特性的优劣决定着高速加工技术水平的高低。“主轴-轴承”系统作为高速主轴单元的主要回转系统，在高速旋转时，将受到高转速场诱发的高速效应(即离心力效应和陀螺力矩效应)的作用，使其动力学特性相对于静止状态时会发生较大变化。因此，针对“主轴-轴承”系统建立可靠、准确的动力学模型，对于评估该系统动力学特性，预测主轴单元高速性能十分必要，具有重要的科学和工程意义。

“主轴-轴承”系统动力学建模过程中最关键亦是最基础的一步在于对轴承非线性分析模型的建立。上世纪50-60年代，Palmgreen[1]和Jones[2-3]分别是建立滚动轴承静力学和拟动力学分析方法的代表性人物；随后，Harris[4]在其基础上完善并发展了滚动轴承的拟动力学分析理论，成为目前绝大多数滚动轴承非线性分析模型的首选；1978年之后，Gupta[5]建立了滚动轴承的动力学分析模型，但由于滚动轴承运动规律的过于复杂，Gupta的模型对设计和应用指导意义不强[6]。近年来，Zverv等[7]研究了滚动轴承在高转速和高预紧状态下的弹性变形问题，为主轴单元设计时轴承的选型提供了准则；Kang等[8]在改进了Harris的分析模型后，利用有限单元法和曲线拟合技术，研究了深沟球轴承的Hertzian接触问题；此外，Kang等[9]还利用人工神经网络模型计算了滚动轴承的运行刚度； Jedrzejewski等[10]亦在Harris的基础上，着重分析了离心力和陀螺力矩效应对角接触球轴承刚度及变形的影响规律； Guo等[11]将有限单元法和接触力学结合起来，针对不同类型、不同结构参数的滚动轴承进行了分析研究，并将轴承的刚度表达为一个矩阵。

在主轴动力学建模方面，国内外学者做了大量的研究。国外，Nelson[12]基于有限单元法建立转子系统动力学方程时，提出用考虑了剪切效应的Timoshenko梁单元取代经典的Euler梁单元；Lin等[13]基于Timoshenko梁理论和有限单元法建立了高速主轴系统热机耦合有限元模型，但该模型没有体现轴承刚度随转速的非线性；Erturka等[14]分别利用经典Euler-Bernoulli梁和Timoshenko梁建立了“主轴-工具系统”动力学模型，并做了对比分析，同时结合Schmitz等[15]提出的柔度耦合技术，辨识了刀尖点的频响函数，但并未研究转速对动力学特性的影响规律；Shin等[16-17]则在借鉴Harris所得成果时，将热对轴承刚度的影响一并考虑，改写了控制方程并建立了高速主轴系统热机耦合模型，但同样没有系统研究高速效应对高速主轴系统动力学特性的影响机理；Cao等[18]在基于Timoshenko梁理论建立主轴-轴承系统动力学有限单元模型的同时，采用了Harris的滚动轴承分析模型，涵盖了轴承离心力、陀螺力矩等高速效应影响因素。国内，周健斌等[19]运用Hamilton原理针对翼吊式发动机机翼系统进行了动力学研究，从理论出发分析了陀螺力矩对结构固有特性的影响；JIANG等[20]在采用Harris轴承分析模型之后，利用传递矩阵法构建了主轴单元动力学模型；张耀强等[21]针对旋转机械建立了滚动轴承-Jeffcott刚性转子系统的非线性动力学方程，并分析了该系统的非线性动力响应行为；汪博等[22]以某立式加工中心主轴系统为研究对象，在建立系统动力学模型的基础上，考察了刀柄与主轴前端锥孔结合面特性对轴端传函的影响规律；吕浪等[23]建立了电主轴单元机电耦合动力学模型，并分析了系统匹配特性。

研究表明：基于非线性滚动轴承分析模型建立“主轴-轴承”系统动力学模型的同时，全面系统地研究高速效应影响规律，对于探索高速主轴单元处于不同转速场时的动力学特性是十分必要的。因此，本文首先采用理论建模与实验建模相结合的方法建立了准确的系统动力学数字模型；然后在此基础上逐一研究了高转速场诱发的各种高速效应对系统动力学特性的影响规律。

由于本文旨在研究高速效应对“主轴-轴承”系统动态特性的影响规律，热效应是进一步研究问题，在本文不在考虑范畴之内，故忽略热效应。

1 “主轴-轴承”系统动力学建模

1.1 角接触球轴承非线性模型

1.1.1 角接触球轴承的Hertzian接触

角接触球轴承的刚度从本质上看，可以认为是滚动体与内、外圈的接触刚度串联的结果[6]。一般的，滚动体和内、外圈之间的Hertzian接触有如下关系：

(1)

式中：Qij,Qej分别为第j个滚动体与内、外圈的接触力；kij,kej分别为第j个滚动体与内、外圈的赫兹接触系数；δij,δe分别为第j个滚动体与内、外圈的接触变形。

则不难得球与内、外圈的接触刚度：

(2)

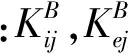
1.1.2 角接触球轴承的变形协调和受力平衡

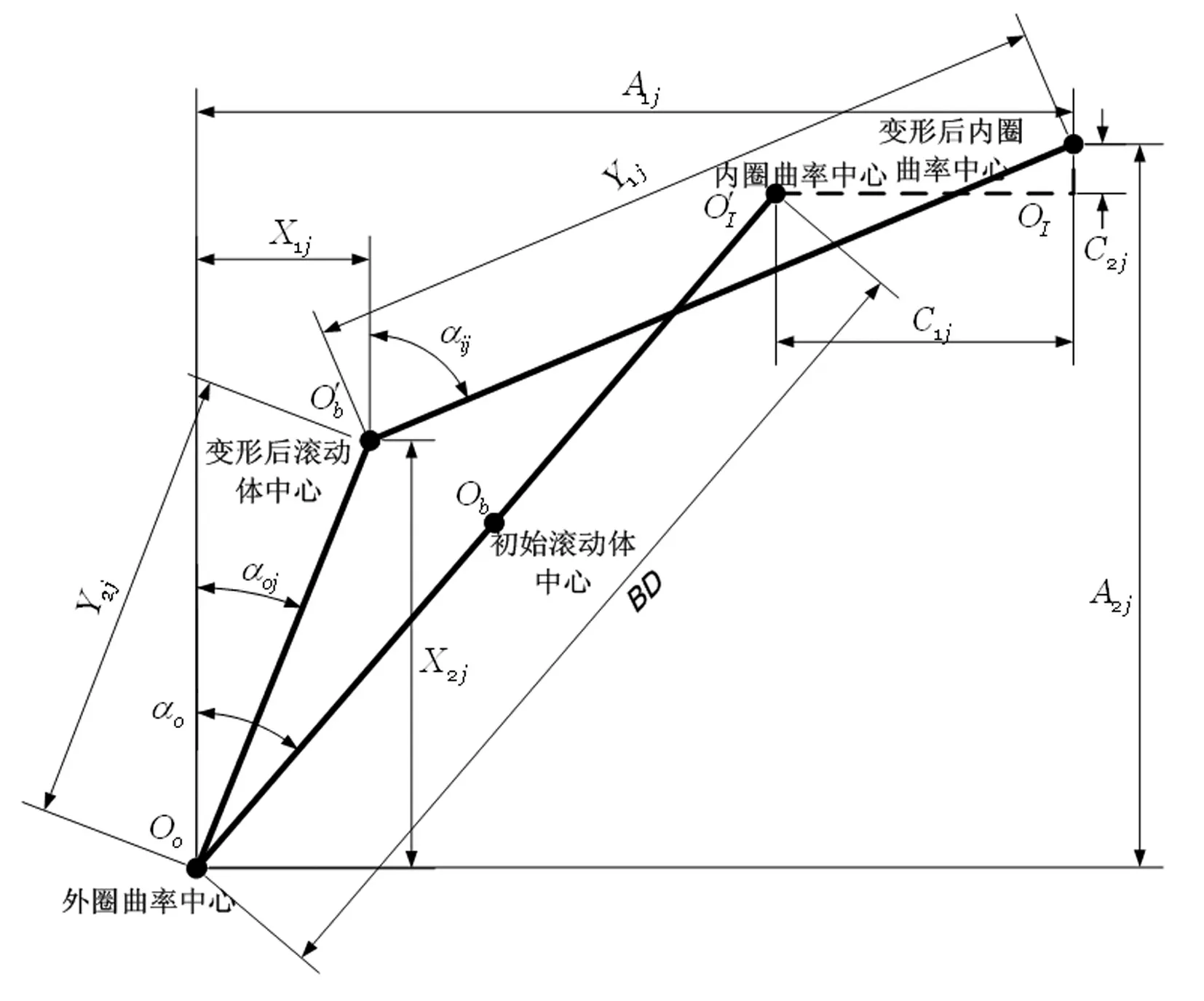
图1 滚动体与内外滚道变形协调关系Fig.1 Deformed relationship between rolling element and rings

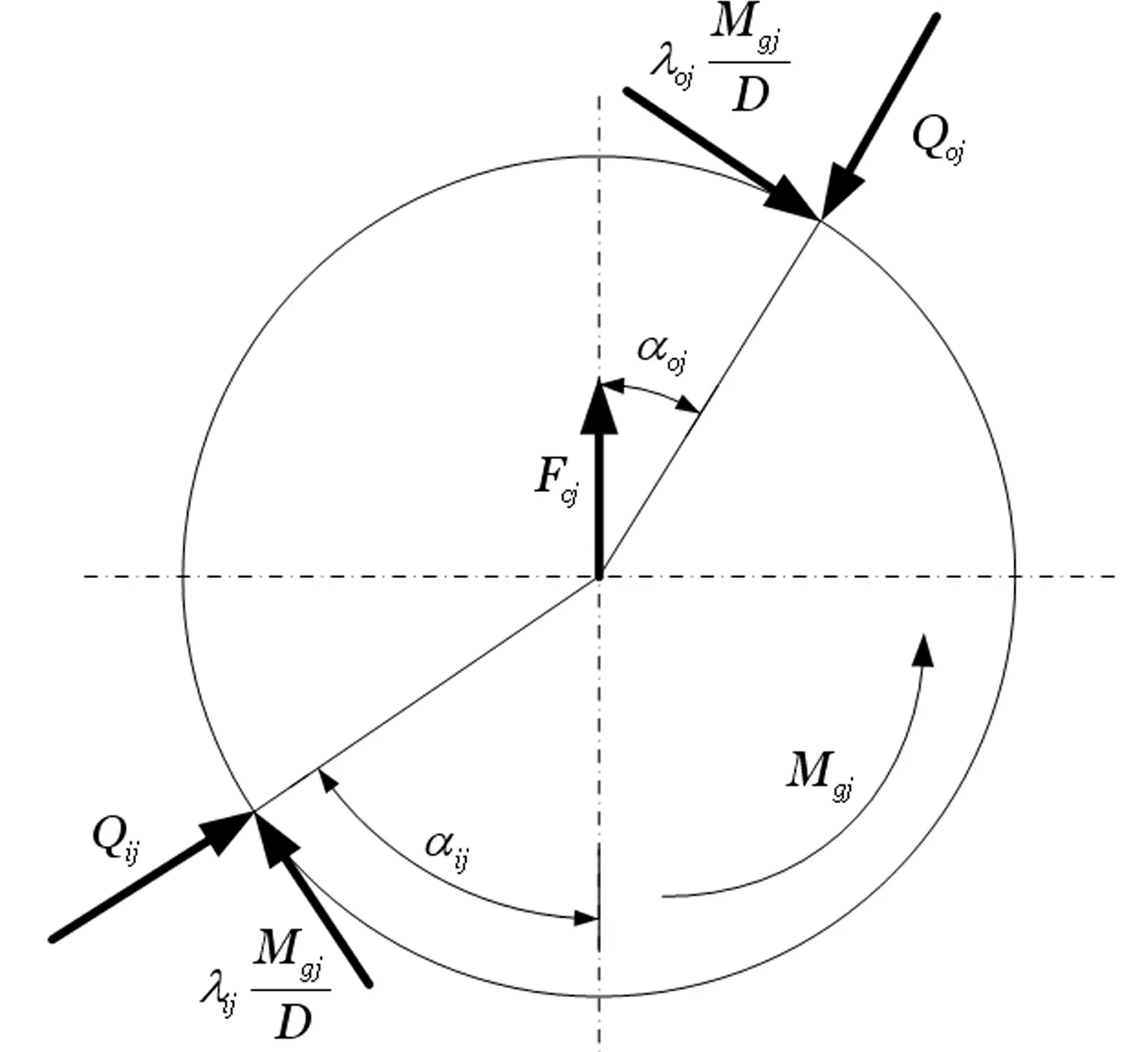
图2 滚动体受力分析Fig.2 Mechanical analysis of rolling element

图3 滚动轴承方位角示意图Fig.3 Azimuth of rolling bearing

从微观的角度出发，角接触球轴承在静止、未预紧状态下内外圈曲率中心与球中心共线，内、外圈接触角相等；而在高速旋转时，由于离心力的作用会导致内圈接触角增大，同时外圈接触角减小。高速时，不失一般性的假设外圈曲率中心固定，因此有如图1所示的轴承内部变形协调关系，进而可建立式(3)-式(8)的轴承几何变形协调方程组；此外，高速时滚动体受到离心力和陀螺力矩的作用，故有如图2所示的滚动体受力分析，结合图3所示滚动轴承方位角示意图，于是得到式(9)-式(12)所示的滚动体受力平衡方程组。

(3)

(4)

(5)

(6)

(A1j-X1j)2+(A2j-X2j)2-

[(fi-0.5)D+δij]2=0

(7)

X1j2+X2j2-[(fe-0.5)D+δej]2=0

(8)

Qijsinαij-Qejsinαej-

Mgj(λijcosαij-λejcosαej)/D=0

(9)

Qijcosαij-Qejcosαej-

Mgj(λijsinαij-λejsinαej)/D+Fcj=0

(10)

Fcj=(ρπD2Dmω2)/12

(11)

Mgj=J(ωR/ω)j(ωR/ω)jω2sinβ

(12)

从宏观的角度来看，各滚动体受力在轴向、径向上的分量之和应与内圈(或外圈)所受外力平衡，故有式(13)-式(15)的滚动轴承内圈(或外圈)受力平衡方程组。公式(3)-(15)中符号意义可参考文献[4]。

(13)

(14)

(15)

在给定转速、轴向和径向载荷的前提下假定δa、δr、γ、X1j、X2j、δij、δej初值，利用Newton-Raphson法联立求解式(3)-式(15)组成的非线性方程组，迭代收敛后获得各个球的内外接触角αij与αej、内外滚道接触变形δij与δej，以及内外滚动接触力Qij与Qej等，进而可利用(2)式计算轴承接触刚度。

1.1.3 角接触球轴承耦合刚度矩阵

角接触球轴承在运转时，内、外圈均同时承受轴向力Fa、径向力Fr和力矩载荷M，因此轴承内、外圈相对轴向变形δa，径向变形δr和转角γ应理解为不同载荷耦合作用的结果，而并非某单一载荷的作用。基于以上思路，结合Harris滚动轴承非线性分析理论，定义同时考虑轴承转速、轴承内外圈变形以及轴承内外圈承载等因素在内的耦合刚度矩阵Kcb：

Kcb=A[n，Defi，Defe，Ldi，Lde]

(16)

式中：KCB为轴承耦合刚度矩阵；n为轴承转速；Defi，Defe为轴承内圈和外圈变形向量；Ldi，Lde为轴承内圈和外圈联合载荷向量 。

滚动轴承耦合刚度矩阵的概念具有一般性，可以作为完备的轴承模型使用于不同种类的转子系统动力学研究，在高速主轴单元动力学建模中更起到积极作用。

“主轴-轴承”系统运转时，滚动轴承内、外圈均同时承受轴向力Fx、径向力Fy、Fz，和力矩载荷My、Mz，因此将内、外圈的位移向量写为[δix,δiy,δiz,γiy,γiz,δex,δey,δez,γey,γez]T，角标中i、e代表内圈和外圈，δ、γ则分别代表平动和转动自由度。

针对轴承内圈，将式(13)-式(15)扩展后可写做式(17)-式(21)：

(17)

(18)

(19)

(20)

(21)

再结合1.1.2节迭代计算结果，分别利用式(17)-式(21)对于δix,δiy,δiz,γiy,γiz求导，并写成如下矩阵形式，矩阵中各元素计算方法可参见文献[18]：

(22)

利用式(17)-式(21)对于δex,δey,δez,γey,γez求导可获得KIE。同样的对于外圈受力平衡也可以写出相应的平衡方程式，求导后可得KEI、与KEE，则轴承刚度矩阵为

(23)

一般的，角接触球轴承耦合刚度矩阵的计算流程可如图4所示。

图4 角接触球轴承刚度矩阵计算流程Fig.4 Flow chart of angular ball bearing stiffness matrix calculation procedure

1.2 基于Timoshenko梁理论的“主轴-轴承”系统动力学有限元模型

1.2.1 梁单元动力学有限元模型

在经典的Euler梁理论中，虽然截面承受剪切合力，但是分布剪应力却不产生剪应变[24]。作为该理论的修正，Timoshenko梁理论将截面的转动惯性融合至梁的场方程中(如图5所示)，这对于高速主轴系统进行动力学建模有着足够的适用性与准确性[12]。文献[25]中指出，虽然有限单元法并非最佳系统学建模方法，但对于主轴来说，该方法可较为精确地获取系统低阶特征值及特征向量。

如图5所示，Timoshenko梁挠曲变形引起的转角γ对时间t的导数dγ/dt与梁绕轴心线的转速Ω正交，二者的叉积不为零。因此，只要转速不为零，梁就会产生陀螺效应。

图5 Timoshenko梁变形运动学Fig.5 Timoshenko beam kinematics

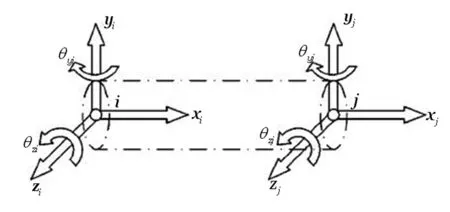
图6 典型旋转梁单元坐标系Fig.6 Reference frame of the typical rotational beam element

如图6所示为2节点(i,j)典型Timoshenko梁单元，其中X向为梁单元轴向。每个节点具有空间3个正交方向的平动自由度和2个绕径向的转动自由度，因此该单元共计10自由度，单元位移向量可写作：

{q}={xi,yi,zi,θyi,θzi,xj,yj,zj,θyj,θzj}

(24)

忽略梁的内部阻尼，利用Hamilton原理可将Timoshenko梁单元动力学方程写为

[Mbm]{q″}-Ω[Gbm]{q′}+

([Kbm]-Ω2[Mbc]){q}={Fbm}

(25)

式中：Mbm、Gbm和Kbm分别为梁单元的质量矩阵、陀螺力矩阵和刚度矩阵；Mbc和Fbm分别为梁单元用于计算离心力的质量矩阵和外力矩阵。

1.2.2 盘单元动力学有限元模型

若将“主轴-轴承”系统中的各类盘套类零件(如轴承隔圈、电机转子等)均视为盘单元，再次利用Hamilton原理则盘单元动力学方程可写为

[Mdisk]{p″}-Ω[Gdisk]{p′}={Fdisk}

(26)

式中：Mdisk、Gdisk和Fdisk分别为盘单元的质量矩阵、陀螺力矩阵和外力矩阵。

1.2.3 “主轴-轴承”系统动力学有限元模型

将Timoshenko梁单元、盘单元及轴承耦合刚度场矩阵联立，即可得“主轴-轴承”系统在其结构阻尼为[Csystem]时的动力学方程为

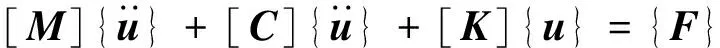
(27)

式中：[M]=[Mbm]+[Mdisk]为系统总体质量矩阵；

[C]=[Csystem]-Ω[Gdisk]-Ω[Gbm]为系统等效阻尼矩阵，其中系统结构阻尼[Csystem]由实验模态分析获取；

[K]=[Kbm]+[Kbpa]-Ω2[Mbc]+[Kbearing]为系统总体刚度矩阵，Kbpa为轴向力引起的刚度项。

2 动力学模型的实验验证方法

某高速加工中心“主轴-轴承”系统结构及主要尺寸如图7所示，该系统前轴承对由4只NSK超高速角接触陶瓷球轴承70BNR10X(结构参数见表2)采用两组“背对背”(Double-Back-to-Back，DBB)配置方式构成，预紧力为285N；后轴承对为单只超高速圆柱滚子轴承N1011RXTPKR；主轴前端刀柄锥孔HSKA63，系统设计最高转速为20 000 r/min。该系统前轴承预紧方式为定位预紧，在装配时通过对并紧螺母施加一定的轴向紧固力，调整内外圈轴向游隙，从而达到轴承出厂设定的预紧状态。

为提高计算速度，建立系统有限元模型时，应忽略如倒角、螺纹等细微特征。有限元模型节点位置的选择主要取决于零件截面尺寸是否发生显著改变，是否与支承零件相连，故节点通常位于主轴台阶处和轴承处。此外，由于固定结合部动力学参数非本文研究内容，故结构中如螺栓结合部等均视为刚性连接。

主轴材料为20CrMnMoH，其他盘套类零件材料均为45#钢。有限元模型中材料属性的选取方案是：密度取7 850 kg/m3，弹性模量取210 GPa，泊松比取0.27。最终建立的“主轴-轴承”系统动力学有限元模型如图8所示。

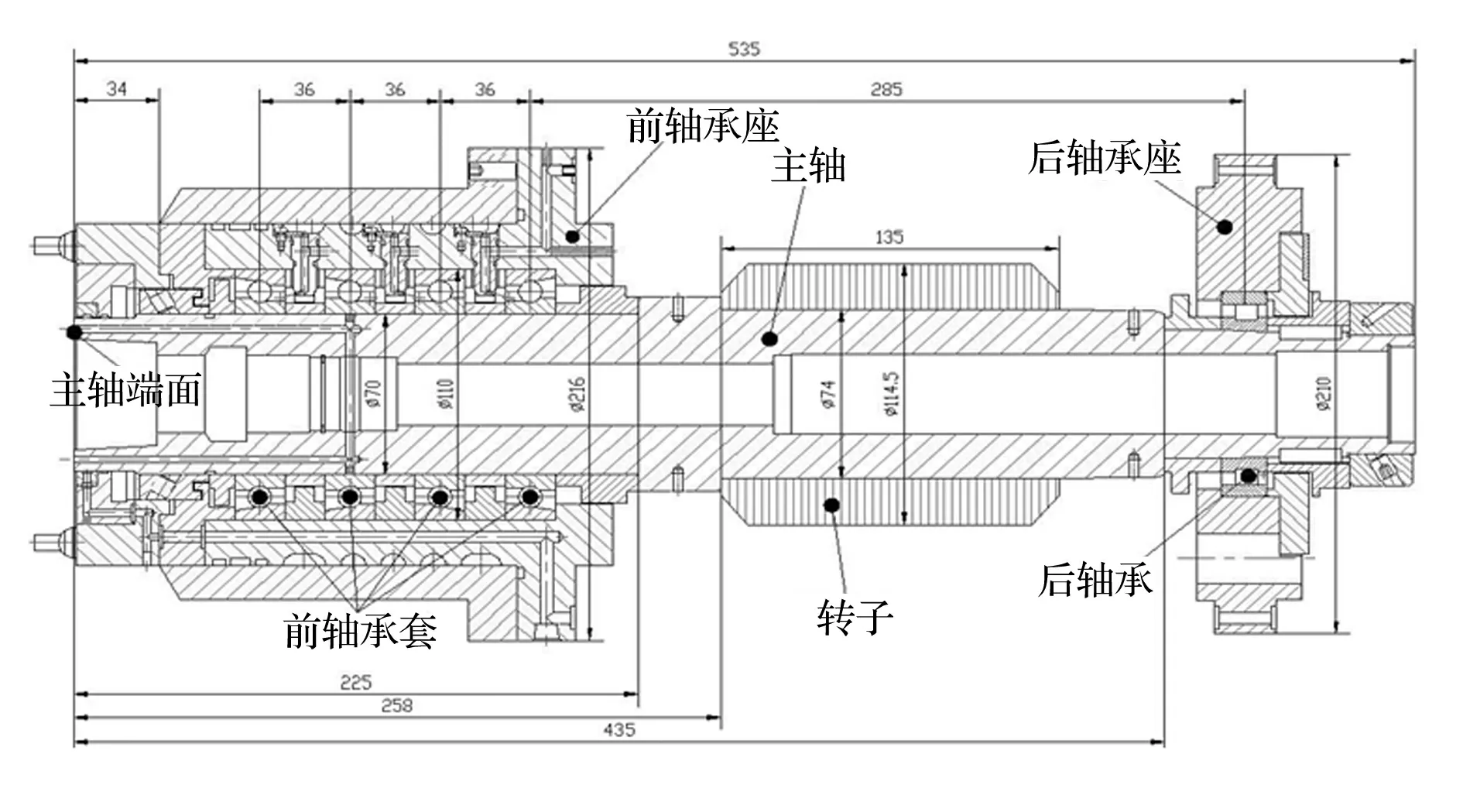
图7 “主轴-轴承”系统简图Fig.7 Sketch of the “shaft-bearing” system

图8 “主轴-轴承”系统有限元模型Fig.8 Finite element model of “shaft-bearing” system

2.2 实验验证

为验证1.2节所建立的“主轴-轴承”系统动力学有限单元模型的准确性，基于LMS Test Lab中的Impact Testing模块进行了该系统锤击模态实验，并拾取系统前端原点频响函数，以便与理论模型计算结果对比。实验时，将系统用橡皮绳悬挂，使其获得最大限度自由度，悬挂点位于前、后轴承套，如图9所示；用力锤锤击系统前端外圆，并利用PCB单向加速度传感器拾取与锤击点相反点和相正交点的振动信号，以提取原点频响Hyy和交叉频响Hyz如图10所示。

图11为“主轴-轴承”系统前端原点频率响应函数Hyy仿真值与实验值对比图，详细结果对比见表1。表中数据显示所建系统动力学有限元模型计算结果与实验值十分吻合，证明了该模型能准确可靠地描述系统在静止状态时的动力学特性。

图9 基于LMS Test Lab的锤击模态实验现场Fig.9 Scene of impact test based on LMS Test Lab

图10 锤击模态实验测点布置Fig.10 Respond points layout of impact modal experimentation

图11 Hyy实验值(虚线)与计算值(实线)对比Fig.11 Experimentation vs. simulation of Hyy

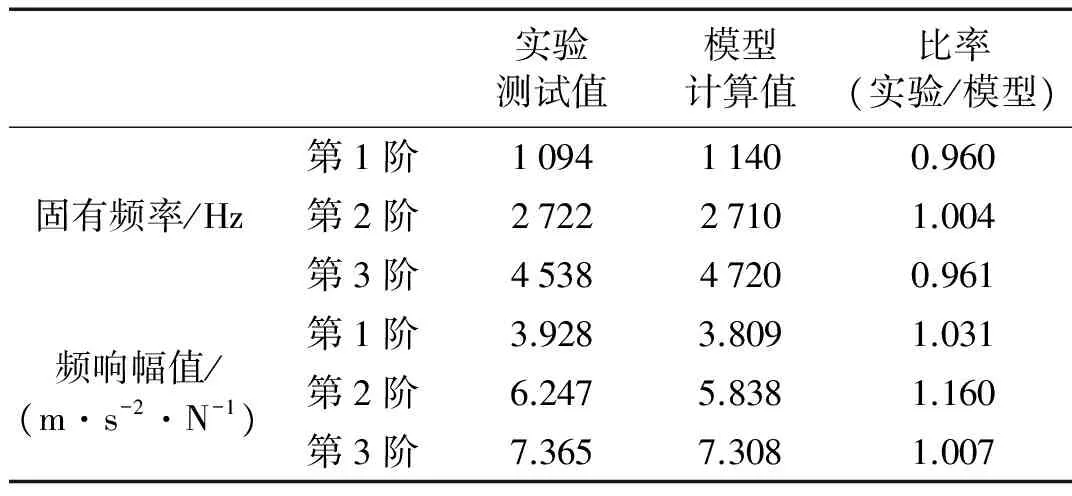
实验测试值模型计算值比率(实验/模型)第1阶109411400．960固有频率/Hz第2阶272227101．004第3阶453847200．961第1阶3．9283．8091．031频响幅值/(m·s-2·N-1)第2阶6．2475．8381．160第3阶7．3657．3081．007

3 “主轴-轴承”高速动态特性研究

所谓高速效应即旋转机械在高速工况时受到的离心力效应和陀螺力矩效应，“主轴-轴承”系统作为一类特殊的旋转机械，在高速旋转时其动力学特性亦会受到高速效应的影响。但各高速效应对系统动力学特性的影响程度并不等同，因此，分别研究主轴离心力效应、主轴陀螺力矩效应以及滚动轴承运行刚度对系统在高速工况下动力学特性的影响规律是十分必要的。

本文基于已建立的“主轴-轴承”系统动力学有限元模型，分以下4种情况较为全面系统的考察了高速效应对于“主轴-轴承”系统动力学特性的影响规律：

① 仅考虑主轴离心力效应的作用；

当距离红豆杉树种播种前半年时间左右，需要用0.5%的高锰酸钾溶液进行红豆杉种子的浸泡，然后等待40min后用清水进行冲洗，并按照树种与细沙的1∶3比例进行混合均匀。这时要保持混合时的沙子含水率在50%～60%，将混合后的树种装于编织袋中，并埋藏在室外的深30～40cm坑中。为了防止其受到水分的影响，需要在坑底进行防水砖的铺设，将混合后的树种用湿沙进行覆盖。直到第二年春天播种的前15天进行掏出备用。在储藏过程中，需要对树种进行定期检查，防止发生霉变，从而使成活率降低。

② 仅考虑陀螺力矩效应的作用；

③ 仅考虑滚动轴承运行刚度的作用；

④ 同时考虑上述3种情况。

3.1 主轴离心力效应分析

由式(25)可知，当主轴转速增大，由于Ω2Mbc项的存在，系统刚度将随之降低，即所谓的主轴“软化”效应，这使得“主轴-轴承”系统的固有频率将会降低。如图12所示，当主轴转速达到20 000 r/min时，系统前3阶主模态固有频率分别下降了13%、0.7%和0.2%。结果表明，离心力效应对于低阶模态的影响明显强于对高阶模态的影响。

图12 仅考虑主轴离心力效应Fig．12Centrifugalforceeffectofshaftonly图13 仅考虑主轴陀螺力矩效应Fig．13Gyroscopicmomenteffectofshaftonly图14 同时考虑主轴离心力效应和陀螺力矩效应Fig．14Centrifugalforceandgyroscopicmomenteffectsofshaftsimultaneously

3.2 主轴陀螺力矩效应分析

根据转子动力学理论[26]，主轴正进动时陀螺力矩使其变形减小，因而提高了主轴的刚度，亦即提高了主轴的固有频率；主轴反进动时陀螺力矩使其变形增大，从而降低了主轴的刚度，主轴的固有频率也随之降低。因此，随着主轴转速的增大，陀螺效应愈发明显，“主轴-轴承”系统各阶主轴主模态固有频率出现了“分岔”的现象，如图13所示。可以看出，陀螺力矩效应与离心力效应对于系统动力学特性的影响有相似之处，即对低阶模态影响强于对高阶模态的影响。此外，陀螺力矩效应对于各阶模态固有频率影响强于离心力效应——当主轴转速达到20 000 r/min时，系统前3阶固有频率降低了17.2%、8.19%和5.55%。图14为同时考虑离心力效应和陀螺力矩效应时，系统前3阶固有频率随转速的变化趋势。

在式(27)中，由于梁单元及盘单元的陀螺矩阵(Gbm和Gdisk)与系统结构阻尼(Csystem)共同组成了系统动力学方程中的阻尼矩阵C，故主轴的正进动和反进动应体现在系统频响函数曲线上。不妨设定主轴转速为10 000 r/min，利用1.2节所建立的动力学模型分别计算当系统阻尼比为0.5%、2%和5%时“主轴-轴承”系统前端原点频响函数Hyy，如图15所示。当系统阻尼比为0.5%时，可以很明显看到5 000 Hz内的3各主模态均出现了两个峰值，分别对应正进动和反进动；随着系统阻尼比的增大，峰值对应的幅值不断减小，且正、反进动对应的波峰逐渐靠拢；当系统阻尼比增大至5%时，原点频响函数Hyy上高阶主模态已经观察不到正、反进动对应的波峰，低阶主模态上亦不明显，说明当系统阻尼比较大时陀螺力矩效应对原点频响函数的影响非常小，几乎已被系统结构阻尼抵消。

然而，此时陀螺力矩效应对交叉频响函数Hyz(或Hzy)影响却较为显著：当主轴处于静止或低速状态时，交叉频响函数幅值极小，可以忽略不计。但当主轴处于高速工况时，由于陀螺力矩效应的存在，将增大交叉频响函数，如图16所示。

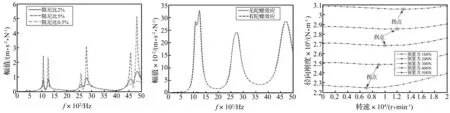
图15 主轴陀螺力矩效应对轴端原点频响Hyy的影响(转速：10000r/min)Fig．15GyroscopicmomenteffectofshaftondirectFRFHyyofspindlenose(Rotationalvelocity：10000r/min．)图16 主轴陀螺力矩效应对轴端交叉频响Hyz的影响(转速：10000r/min，系统阻尼比：5%)Fig．16GyroscopicmomenteffectofshaftoncrossFRFHyzofspindlenose(Rotationalvelocity：10000r/min．Dampingratio：5%)图17 不同预紧力下轴承径向运行刚度Fig．17Radialoperationalstiffnessofbearingvs．variouspreload

3.3 角接触球轴承径向运行刚度分析

NSK轴承70BNR10X基本参数见表2，转速范围为0-20 000 r/min。基于1.1节所述内容计算的轴承在不同预紧力和不同转速下的径向运行刚度如图17所示。图中曲线表明，在设定转速范围内，轴承径向运行刚度随预紧力的增大而增大，随转速增大先减小后增大。

表2 70BNR10X基本参数

图17中轴承的径向运行刚度体现出非单调变化的规律，这与目前大多数文献中一味强调轴承“软化”效应而忽略其“刚化”效应的结论更加全面。产生这一现象的原因是：如图18所示，在不考虑热效应时，随着轴承转速增大，滚动体所受离心力Fc也增大，同时内圈接触角增大而外圈接触角减小。此时滚动体与内圈的接触载荷减小，虽然外圈接触载荷增大，但接触刚度串联的结果是轴承的径向刚度随转速增加而减小。然而，随着转速进一步增大至高转速工况，离心力剧烈增加，滚动体相对于内圈开始出现“爬坡”现象(图18中球轴承运动所指方向)，内圈接触载荷反而变大，此时轴承的径向刚度应随转速的增加而增大。因此，从较宽的转速范围来考虑，角接触球轴承径向刚度随转速增大并非单调减小。当转速在某临界值范围以内变化时，轴承的径向刚度随转速增大而减小；当转速在该范围以外变化时，轴承的径向刚度随转速增大而增大。

图18 角接触球轴承运行状态时的微观几何Fig.18 Micro-geometry of angular contact ball bearing in operational state

图17还表明，轴向预紧力增加后，轴承径向运行刚度随转速变化的曲线拐点所对应转速逐渐增大，亦即拐点随预紧力增大而向高转速段漂移。故不难推测当预紧力增大到一定程度时，拐点将不会出现在给定转速范围内。为验证该推论，根据NSK公司给定的3个参考预紧力：EL(285 N)、L(1 330 N)、M(2 568 N)重新计算70BNR10X轴承在上述3种预紧方案下的径向运行刚度，结果如图19所示，很好的验证了推论的正确性。

由于实际装配工艺中，轴承的预紧力为EL(285 N)，根据“主轴-轴承”系统动力学有限元模型的分析结果，系统前3阶主模态固有频率随转速增大出现先减小后增大的趋势，但频率变化幅度很小，如图20所示。因此说明在该预紧状态下，轴承径向运行刚度并非影响“主轴-轴承”系统高速工况下动力学特性的关键因素。

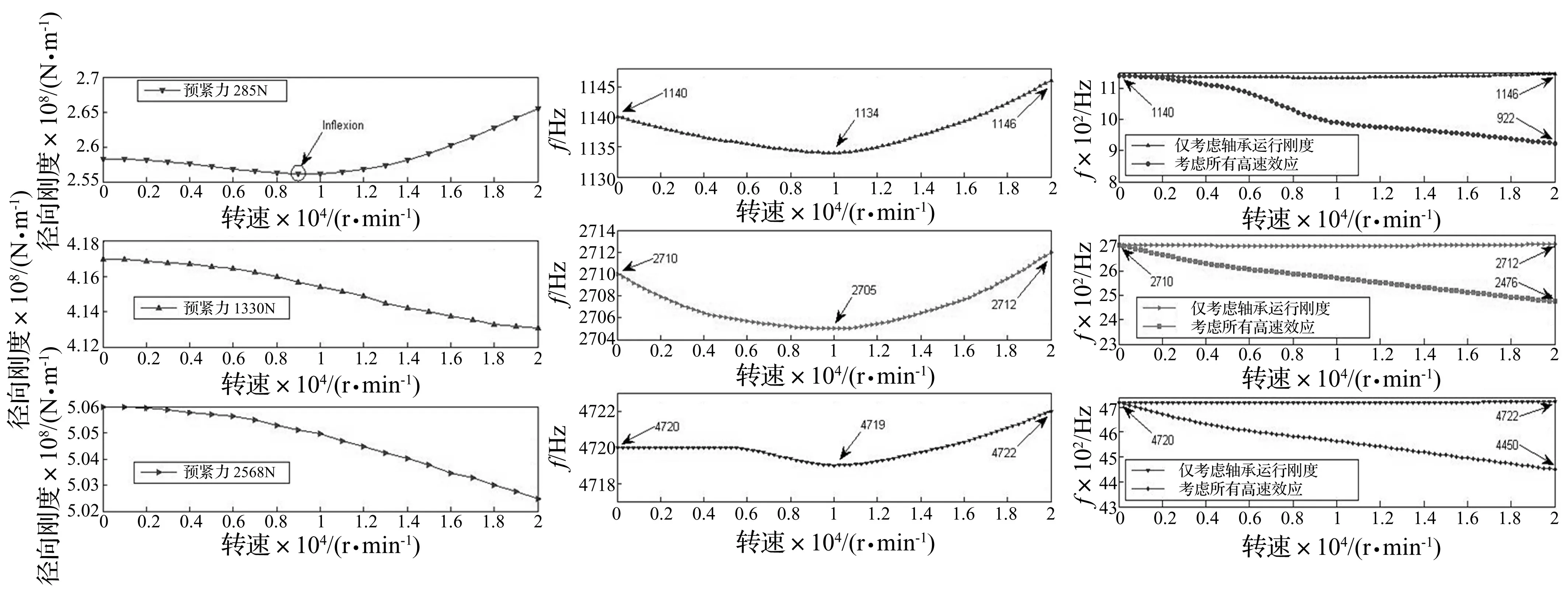
图19 EL预紧、L预紧和M预紧下轴承的径向运行刚度Fig．19Radialoperationalstiffnessof70BNR10Xbearingvs．variouspreload图20 仅考虑滚动轴承运行刚度Fig．20Operationalstiffnessofrollingbearingonly图21 考虑所有高速效应和仅考虑滚动轴承运行刚度时对比Fig．21Highspeedeffectsofbothshaftandbearingvs．highspeedeffectsofbearingonly

3.4 主轴与轴承高速效应综合分析

同时考虑主轴的高速效应和轴承的运行刚度后，“主轴-轴承”系统前3阶主模态固有频率的变化趋势如图21所示，相比起仅考虑轴承运行刚度的情况，变化趋势明显不同。综合3.1-3.3节所述内容可知，在诸多“主轴-轴承”系统高速工况下动力学特性的影响因素中，主轴的高速效应，特别是陀螺力矩效应是最关键的。

4 结 论

为研究高转速场诱发的高速效应对“主轴-轴承”系统动力学特性的影响规律，本文基于理论与实验相结合的建模思想，建立了准确的“主轴-轴承”动力学数字模型，并利用该模型针对高速效应进行了分析，得到以下结论：

(1) 系统低阶模态固有频率相对于高阶受到高速效应的影响更大，且陀螺力矩效应是“主轴-轴承”系统高速工况下动力学特性的关键影响因素，其影响权重大于离心力效应。

(2) 当系统阻尼比较小(如0.5%)时，正、反进动能直接反映在系统前端原点频响函数曲线上，但当系统阻尼比较大(如5%)时，曲线上正、反进动所对应的波峰不明显；此外，陀螺力矩效应对交叉频响函数的影响显著。

(3) 角接触球轴承径向运行刚度随转速增大而非单调变化，轴承刚度-转速曲线的拐点随轴向预紧力增大而向高速段漂移；当预紧力增大至某临界值且观察转速范围较窄时，拐点将不在转速范围之内，此时仅能观察到轴承运行刚度随转速增大而减小。

(4) 相比起滚动轴承的运行刚度，主轴的高速效应(尤其是陀螺力矩效应)对“主轴-轴承”系统高速工况下动力学特性影响更大，是关键影响因素。

上述结论表明，要准确的预测“主轴-轴承”在高转速场中的动力学特性，除了建立滚动轴承非线性模型之外，还须同时考虑离心力和陀螺力矩等高转速场诱发的高速效应。模型的建立具有一定的科学和工程意义，为下一阶段研究切削稳定性提供了数据支持。

[ 1 ] Palmgren A. Ball and roller bearing engineering, 3rded [M]. Philadelphia: Burbank, 1959.

[ 2 ] Jones A B. Ball motion and sliding friction in ball bearings[J]. Journal of Basic Engineering, 1959, 3: 1-15.

[ 3 ] Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed condition[J]. Journal of Basic Engineering, 1960, 82(2): 309-320.

[ 4 ] Harris T A. Rolling bearing analysis, 3rd[M]. John Wiley & Sons, Inc. 1990.

[ 5 ] Gupta P K. Advanced dynamics of rolling elements [M]. New York: Springerverlag, 1984.

[ 6 ] 蒋兴奇. 主轴轴承热特性及对速度和动力学性能影响的研究[D]. 杭州：浙江大学, 2001.

[ 7 ] Zverv I, Pyoun Y S, Lee K B, et al. An elastic deformation model of high speed spindles built into ball bearings[J]. Journal of Materials Processing Technology， 2005， 170(3): 570-578.

[ 8 ] Kang Y, Shen P C, Huang C C, et al. A modification of the Jones-Harris method for deep-groove ball bearings[J]. Tribology International, 2006，39(11): 1413-1420.

[ 9 ] Kang Y, Huang C C, Lin C S, et al. Stiffness determination of angular-contact ball bearings by using neural network[J]. Tribology International, 2006，39(6): 461-469.

[10] Jedrzejewski J, Kwasny W. Modelling of angular contact ball bearings and axial displacements for high-speed spindles[J]. CIRP Annals-Manufacturing Technology, 2010，59(1): 377-382.

[11] Guo Y, Parker R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model[J]. Mechanism and Machine Theory, 2012,51: 32-45.

[12] Nelson H D. A finite rotating shaft element using Timoshenko beam theory[J]. Journal of Mechanical Design, 1980, 102(2): 793-803.

[13] Lin C W, Tu J F, Kamman J. An integrated thermo-mechanical-dynamic model to characterize motorized machine tool spindles during very high speed rotation[J]. International Journal of Machine Tools & Manufacture, 2003, 43(10): 1035-1050.

[14] Erturka A, Ozguvena H N, Budak E. Analytical modeling of spindle tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF[J]. International Journal of Machine Tools & Manufacture, 2006, 46(15): 1901-1912.

[15] Schmitz T L, Davies M A, Kennedy M D. Tool point frequency response prediction for high-speed machining by RCSA[J]. Journal of Manufacturing Science and Engineering,2001, 123(4):700-707.

[16] Li H Q, Shin Y C. Integrated dynamic thermo-mechanic modeling of high speed spindles:part 1-model development[J]. Journal of Manufacturing Science and Engineering, 2004,126(1): 148-158.

[17] Li H Q, Shin Y C. Integrated dynamic thermo-mechanic modeling of high speed spindles:,part 2- solution procedure and validations[J]. Journal of Manufacturing Science and Engineering, 2004, 126(1): 159-168.

[18] Cao Y Z, Yusuf A. A general method for the modeling of spindle-bearing systems[J]. Journal of Mechanical Design, 2004, 126(6): 1089-1104.

[19] 周健斌,章俊杰,孟光. 计及陀螺效应的翼吊式机翼-发动机系统结构动力学特性研究[J].振动与冲击, 2012, 31(6): 145-149. ZHOU Jian-bin, ZHANG Jun-jie, MENG Guang. Structural dynamic characteristics of a wing-engine system with gyro effects[J]. Journal of Vibration and Shock, 2012, 31(6): 145-149.

[20] JIANG Shu-yun, ZHENG Shu-fei. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics[J].International Journal of Machine Tool & Manufacture, 2010, 50: 131-142.

[21] 张耀强, 陈建军, 唐六丁,等. 滚动轴承-JEFFCOTT转子系统非线性动力响应分析[J]. 振动与冲击, 2008, 27(5): 56-59. ZHANG Yao-qiang, CHEN Jian-jun, TANG Liu-ding, et al. Analysis of nonlinear dynamic response of a rolling bearing-jeffcott rotor system[J]. Journal of Vibration and Shock,2008, 27(5): 56-59.

[22] 汪博, 孙伟, 太兴宇,等. 主轴系统结合面对主轴系统动力学特性的影响分析[J]. 振动与冲击,2011, 30(10): 231-235. WANG Bo, SUN Wei, TAI Xing-yu, et al. Effect of interfaces on dynamic characteristics of a spindle system[J]. Journal of Vibration and Shock,2011, 30(10): 231-235.

[23] 吕浪, 熊万里, 侯志泉. 面向机电耦合振动抑制的电主轴系统匹配特性研究[J]. 机械工程学报, 2012, 48(9)：144-154. LV Lang, XIONG Wan-li, HOU Zhi-quan. Research on match characteristics of a motorized spindle system to suppress electromechanical coupling vibration[J]. Journal of Mechanical Engineering, 2012, 48(9)：144-154.

[24] 金斯伯格J H. 机械与结构振动——理论与应用[M]. 北京：中国宇航出版社，2005.

[25] 高尚晗,孟光. 机床主轴系统动力学特性研究进展[J].振动与冲击, 2007，26(6): 103-109. GAO Shang-han, MENG Guang. Advances in research on dynamic characteristics of machine tool spindle[J]. Journal of Vibration and Shock, 2007， 26(6): 103-109.

[26] 钟一谔, 何衍宗，等. 转子动力学[M].北京：清华大学出版社, 1987.

Dynamic performance of a shaft-bearing system with centrifugal force and gyroscopic moment effects

HU Teng， YIN Guo-fu， SUN Ming-nan

(School of Manufacture Science and Engineering, Sichuan University, Chengdu 610065, China)

In order to improve the operation stability of a spindle system with high speeds, it is significant to investigate its dynamic performance with centrifugal force and gyroscopic moment effects. An integrated shaft-bearing system’s dynamic model considering both centrifugal force and gyroscopic moment effects was presented based on coupled stiffness matrices of rolling bearings obtained by extending Harris’ nonlinear rolling bearing analysis model. Impact modal tests were conducted to verify the correctness of this dynamic model. The effects of centrifugal force and gyroscopic moment of the shaft and operational stiffness of rolling bearings on the dynamic performance of the shaft-bearing system with a high speed were analyzed. It was shown that when the bearing is in the case of extreme light (EL) preload, the high-speed effects of the shaft have a greater influence on the dynamic performance of the shaft-bearing system than the operational stiffness of rolling bearings does; the gyroscopic moment effect of the shaft is the most remarkable influence factor.

high-speed field; shaft-bearing system; dynamic performance; centrifugal force; gyroscopic moment

“高档数控机床与基础制造装备” 科技重大专项课题(SK201201A26-01)

2013-01-28 修改稿收到日期：2013-06-04

胡腾 男，男，博士生，1982年9月生

TH113

A

10.13465/j.cnki.jvs.2014.08.018