含PID控制器的迟滞非线性控制系统的主共振及奇异性

熊 蕊， 刘向东

(北京理工大学 自动化学院，北京 100081)

含PID控制器的迟滞非线性控制系统的主共振及奇异性

熊 蕊， 刘向东

(北京理工大学 自动化学院，北京 100081)

针对含PID控制器的迟滞非线性闭环控制系统，用Backlash神经网络模型逼近系统迟滞非线性部分，建立动力学模型。研究了系统在简谐激励下的主共振，利用平均法得到了系统的分岔方程，并用奇异性理论进行了分析，得到了转迁集和分岔图。另外还研究了系统参数对开折参数和分岔参数的影响，从而为系统参数的选择提供理论指导。

迟滞；非线性控制系统；Backlash神经网络模型；主共振；奇异性理论

迟滞非线性是很常见的系统非线性特性，其主要特点是多值性、非光滑性和记忆特性，非常容易产生复杂动力学行为如分岔、混沌等。在实际工程中，具有迟滞非线性的材料有很多，如钢丝绳、形状记忆合金、磁致伸缩材料、压电陶瓷等。迟滞非线性研究涉及机械系统隔振、地震工程、土木工程等多个领域。

对系统进行分岔分析可以对系统的控制和系统参数的选择提供理论指导。目前用来描述迟滞现象的主要模型有双线性模型、Davidenkov模型、Bouc-wen模型、多项式模型、Preisach模型等。近年来，关于迟滞非线性系统的动力学研究得到了很大的发展。文献[1-2]研究了具有间隙的双线性迟滞系统的周期、倍周期以及混沌振动及其出现特点，计算结果表明在特定的参数范围内系统出现无序的混沌运动。文献[3]建立了一类含Davidenkov迟滞环的非线性相对转动动力学方程，分别分析了该非线性相对转动自治方程和微外扰下非自治方程的分岔特性，得到了几种分岔结构及外扰下全局分岔图。文献[4]用Peisach模型来建模van der pol振荡系统中的迟滞部分，并分析了系统的Hopf分岔.文献[5]研究了周期激励下含Preisach迟滞的非线性方程的分岔特性。文献[6-7]研究了含Bouc-Wen迟滞的SODF振荡器系统迟滞参数对迟滞系统的分岔与混沌的影响。文献[8]将改进的三次多项式迟滞模型用于描述压电材料的弹性迟滞非线性特性，用多尺度法求解定子的一次近似主共振响应，发现了定子主共振响应中存在振幅跳跃和多解现象。

奇异性理论体系的形成为动力系统的分岔分析开辟了一条新的途径。奇异性理论在迟滞系统中也得到了一定的应用。文献[9]针对一类单自由度迟滞-自激振动系统的分岔，提出了转迁集的概念，并利用奇异性理论分析了不同参数区域内的保持分岔图。文献[10]研究了含Bingham迟滞模型的汽车悬架在简谐路面激励作用下的亚谐共振，分析了系统参数对开折参数和分岔参数的影响。文献[11]将多尺度法与奇异性理论相结合得到了含Davidenkov模型的迟滞非线性系统的分岔转迁集，讨论了开折参数与原参数之间的关系。

Backlash算子[12]是连续算子，具有迟滞特性，且有限个Backlash迟滞算子可以以任意精度对迟滞环进行建模，具有容易辨识的优点。因此，本文采用迟滞非线性的Backlash神经网络模型逼近系统迟滞非线性部分，可以解决一些迟滞模型不适用于常规方法进行动力学分析或计算过程繁杂的问题。目前，针对控制系统的非线性动力学研究还很少，而PID控制器已在工程实际中有了广泛的应用。因此，本文针对含PID控制器的迟滞非线性闭环非自治迟滞系统，首先用Backlash神经网络模型来表示系统迟滞非线性部分，建立动力学模型。然后研究了系统在简谐激励下的主共振，利用平均法得到了系统的分岔方程，并用奇异性理论进行了分析，得到了转迁集和分岔图。另外还研究了系统参数对开折参数和分岔参数的影响。

1 含PID控制器的迟滞非线性闭环非自治系统模型和方程

考虑如图1所示的含PID控制器的迟滞非线性闭环系统，被控对象可以看作一个迟滞非线性环节加上一个二阶振荡环节构成。这里，m、b、c为系统的质量、阻尼，刚度；k、kd、ki分别为比例、微分、积分控制器系数；x(t)表示系统的输出；u(t)表示施加于被控对象的输入；y(t)表示被控对象迟滞非线性环节的输出；f表示周期激励的幅值；Ω表示周期激励频率。

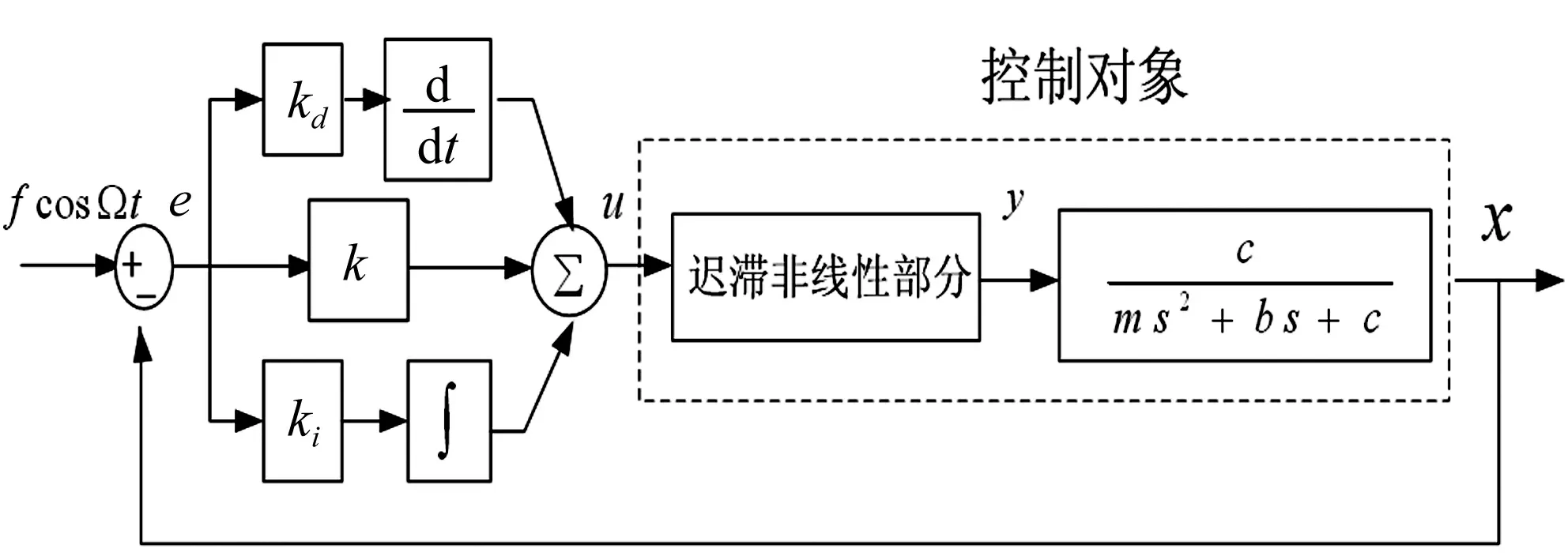
图1 含PID控制器的迟滞非线性闭环系统Fig.1 Nonlinear hysteretic loop system with PID controller

本文采用迟滞非线性的Backlash神经网络模型，利用Backlash算子，将有限数量个不同宽度的Backlash算子进行叠加，来逼近该闭环系统中的迟滞非线性部分，如图2所示。这种神经网络建立的模型在开展动力学分析的时候能大大简化计算过程，且误差在可接受的范围内。

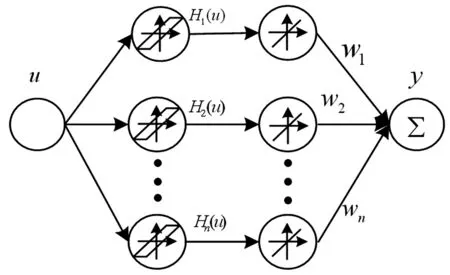
图2 系统迟滞非线性部分Backlash神经网络模型Fig.2 Backlash neutral network model for hysteretic nonlinear block

综上可写出该迟滞非线性闭环系统动力学方程：

(1)

2 主共振分岔

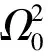
(2)

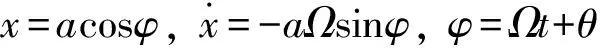
设τ=εt，根据平均法有：

(3)

其中，

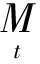
设方程(2)的第一次近似解为

x=acos(Ωt+θ)

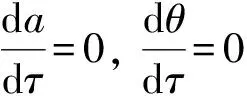
D1+D2cosθ+D3sinθ=0

D4+D3cosθ-D2sinθ=0

(4)

其中，

由式(4)消去循环坐标θ，得到分岔方程

(5)

基于压电陶瓷执行器的控制系统是一类典型的迟滞非线性控制系统。本文以Low等[13]提出的压电陶瓷Bouc-Wen迟滞模型作为图1所示迟滞非线性控制系统的控制对象，该模型采用一阶微分方程来描述迟滞非线性环节，数学方程如下：

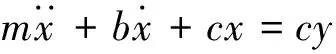
y=de·u-z

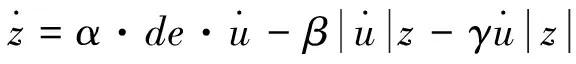
(6)

其中，x(t)表示整个压电系统的输出；z(t)表示迟滞非线性动态的输出变量；u(t)表示施加于压电执行器的输入电压；de表示压电系统有效压电系数；α,β,γ为影响迟滞曲线形状的参数。模型(6)的参数采用文献[13]给出的参数取值，m=1.595×10-2kg，b=1.169 N·s/m，c=3.197×103N/m，de=1.014 m/V，α=4.297×10-1,β=3.438×10-2,γ=-2.865×10-3。

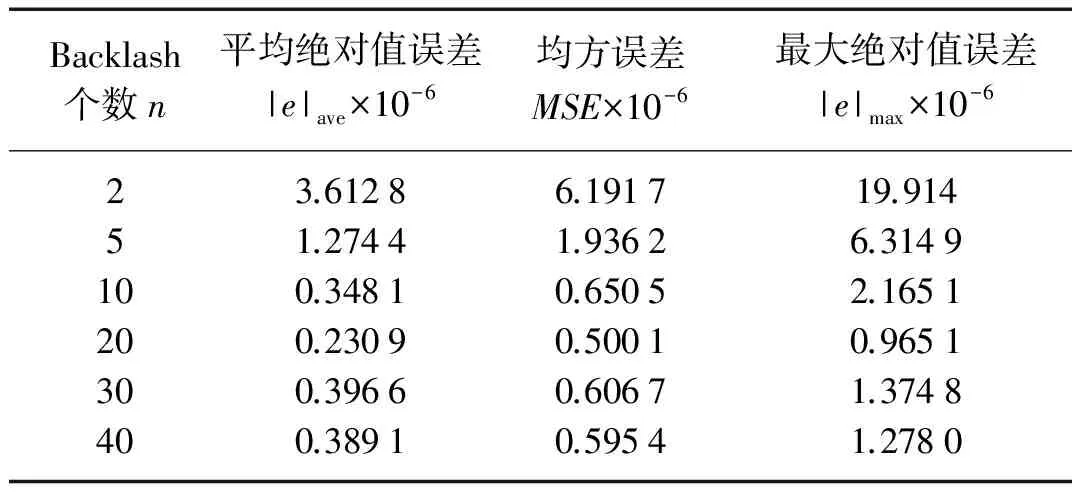
表1 Backlash神经网络模型训练后的误差

将不同个数Backlash算子训练的误差进行比较得到表1。由表1可以看出在网络中选择Backlash层算子个数为20时训练误差达到最小值，建模效果最好。因此取n=20，对应的加权值取值如表2所示。

表2 Backlash神经网络模型各加权系数值

将以上各参数值代入(5)式，对(5)式中的反正弦函数和根式进行级数展开化简，可得：

(7)

a4+a3a3+a2a2+a1a+a0=0

(8)

其中，

0.341 6Ω2+0.017 5kdki-6.36×10-5σ2-0.002 7σk)

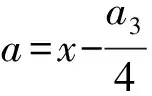
(9)

令

则

x4-λ+ε1x+ε2x2=0

(10)

式(10)为范式x4-λ=0的普适开折，称之为四次折叠分岔，其余维数为2。根据转迁集的定义很容易求出普适开折G(x,λ,ε)=g+ε1x+ε2x2=x4-λ+ε1x+ε2x2的转迁集。

分岔点集：B=φ(空集)

双极限点集：D={ε1=0,ε2≤0}

转迁集：Σ=B∪H∪D

转迁集Σ将开折参数ε1-ε2平面分成几个不同的区域，如图3所示。在同一区域中，即使分岔参数变化，其分岔方程的分岔图也将保持相同拓扑结构，这样的分岔图称为保持的，而转迁集上的分岔图称为非保持的。分岔图如图4所示。图4中，七种分岔模式反应了该系统在正弦激励作用下的全部信息。通过调节开折参数，可以使系统具有不同的动力学行为，而开折参数的控制，可通过调节系统的参数来实现。因而，研究系统参数与开折参数的关系可以为系统参数的选择提供理论指导以达到所期望的动力学行为。

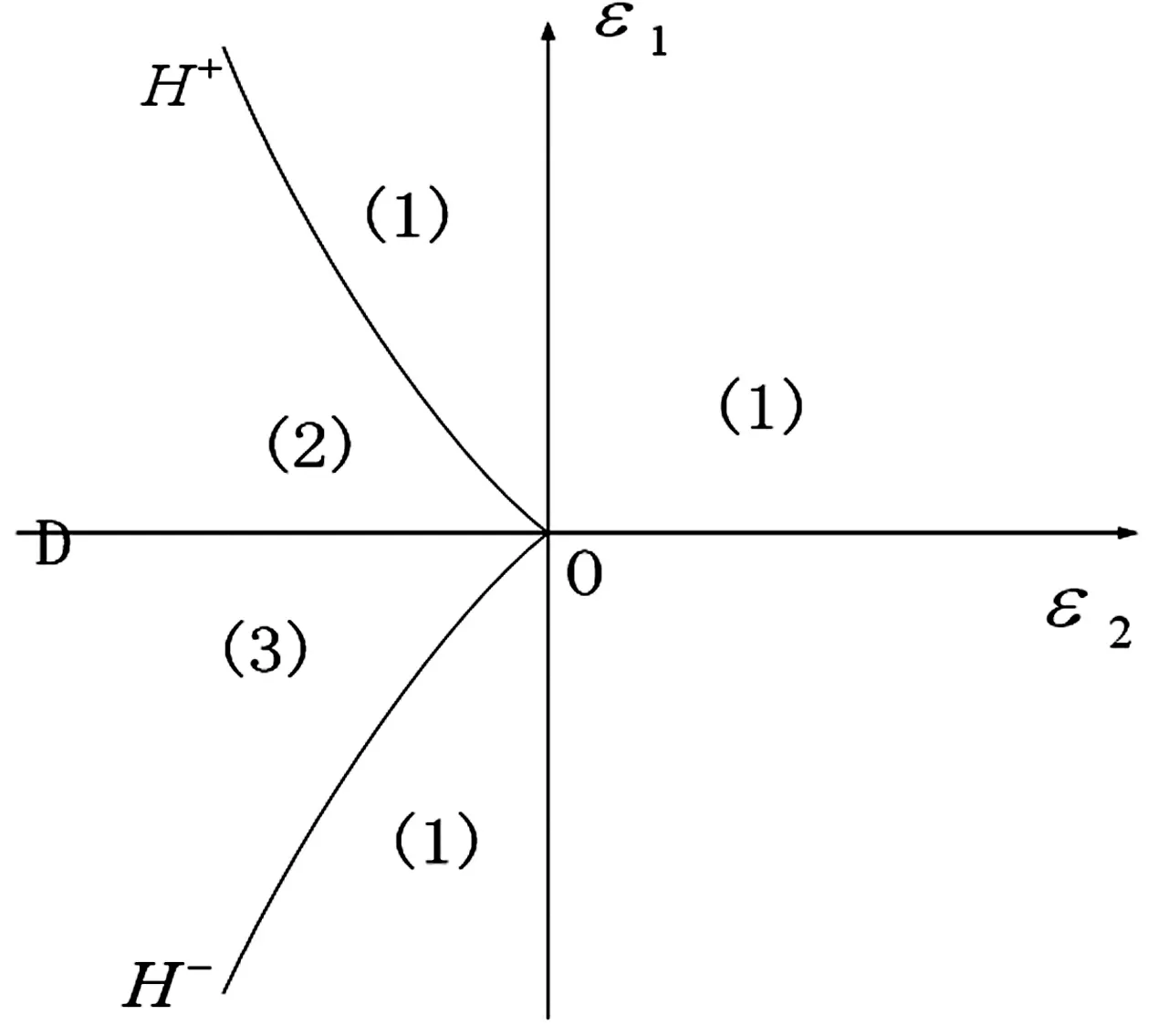
图3 系统转迁集Fig.3 Transition sets of bifurcation equation of system

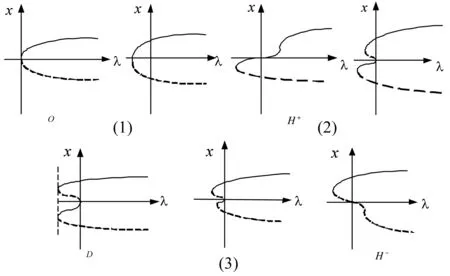
图4 系统分岔图Fig.4 Bifurcation diagram of bifurcation equation of system

3 开折参数对系统参数的依赖性

以上的分析中，采用的开折参数并不是独立的系统参数，而是系统参数的组合，得到的分岔模式并不是在每个具体系统中都会发生。下面，我们研究开折参数对原系统参数k、kd、ki、f、Ω的依赖关系，从而得到系统参数的变化对系统动力学行为的影响。画出开折参数与系统参数的依赖关系图如图5所示。

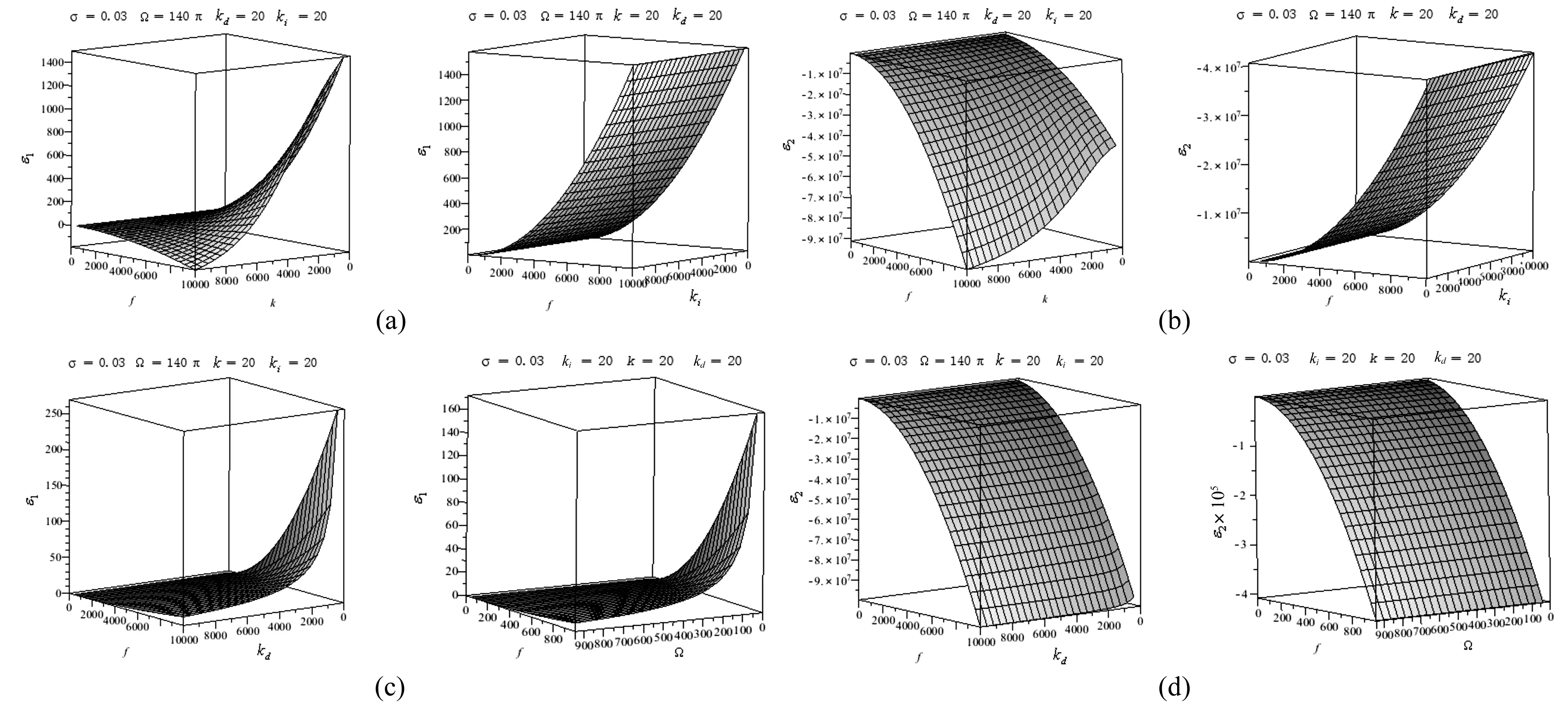
图5 开折参数与系统参数的关系Fig.5 Relations between the unfolding parameters and the system parameters

4 结 论

本文针对含PID控制器的迟滞非线性非自治闭环系统，用Backlash神经网络模型表征系统迟滞非线性部分以解决一些迟滞模型不适用于常规方法进行动力学分析或计算过程繁杂的问题。将平均法应用于该类控制系统在简谐激励下的主共振的研究，得到系统的分岔方程。并将奇异性理论推广应用到该类迟滞控制系统中进行分析，得到了系统的分岔图。另外通过建立系统参数k、kd、ki、f、Ω与开折参数的关系，研究了系统参数对系统分岔特性的影响。研究表明，该系统的响应为四次折叠分岔，激励幅值f、控制器比例系数k、微分系数kd对普适开折参数的影响较大，ki的改变对开折参数影响不大。激励幅值较小时，激励频率Ω对开折参数的影响较小。而激励幅值较大时，激励频率Ω对开折参数的影响较大。通过研究系统参数与开折参数之间的关系，我们可以发现这些系统参数的不同取值可以使系统出现不同的分岔特性，从而我们可以根据所期望的分岔特性选择系统控制器参数和给定输入参数。该研究成果对工程实际中的该类迟滞非线性控制系统的分岔与控制研究具有一定的指导作用和应用价值。

[ 1 ] Li H G, Zhang J W, Wen B C. Chaotic behaviors of a bilinear hysteretic oscillator[J]. Mechanics Research Communications, 2002, 29(5):283-289.

[ 2 ] 李鸿光，孟光，闻邦椿. 带间隙的双线性滞回系统的非线性振动[J]. 机械工程学报,2004, 40(7)：10-13. LI Hong-guang, MENG Guang, WEN Bang-chun. Nonlinear oscillation of bilinear hysteresis system with clearance[J]. Chinese Journal of Mechanical Engineering,2004, 40(7):10-13.

[ 3 ] 侯晓东，刘彬，时培明. 一类滞后相对转动动力学方程的分岔特性及其解析近似解[J]. 物理学报, 2009, 58(9): 5942-5948. HOU Xiao-dong, LIU Bin, SHI Pei-ming. The bifurcation of a kind of relative rotational dynamic equation with hysteresis and its approximate solution[J]. Acta Physica Sinica, 2009,58(9):5942-5948.

[ 4 ] Appelbe B，Rachinskii D，Zhezherun A. Hopf bifurcation in a van der Pol type oscillator with magnetic hysteresis[J]. Physica B：Condensed Matter,2008,403(2-3):301-304.

[ 5 ] Krasnosel’skii A，Rachinskii D. Bifurcation of forced periodic oscillations for equations with Preisach hysteresis[J]. Journal of Physics:Conference Series, 2005,22:93-102.

[ 6 ] LI Hong-guang，MENG Guang. Nonlinear dynamics of a SDOF oscillator with Bouc-Wen hysteresis[J]. Chaos Solitons & Fractals,2007,34(2):337-343.

[ 7 ] 李鸿光，何旭，孟光. Bouc-Wen滞回系统动力学特性的仿真研究[J]. 系统仿真学报,2009,16(9)：2009-2011. LI Hong-guang，HE Xu，MENG guang. Numerical simulation for dynamic characteristics of Bouc-Wen hysteretic system[J]. Journal of System Simulation,2009,16(9):2009-2011.

[ 8 ] 曹树谦，付耀东，贺微波.基于三次迟滞模型的超声电机圆环定子主共振响应[J].振动与冲击,2009, 28(1)：38-41. CAO Shu-qian, FU Yao-dong, HE Wei-bo. Primary resonance of a ring-type stator of ultrasonic motors based on cubic polynomial hysteresis model[J]. Journal of Vibration and Shock，2009,28(1):38-41.

[ 9 ] 杨绍普，陈予恕. 一类单自由度滞后-自激振动系统的分叉[J].振动工程学报, 1991,4(2):95-101. YANG Shao-pu，CHEN Yu-shu. Bifurcation of single degree of freedom and self-excited vibration system[J]. Journal of Vibration Engineering, 1991，4(2):95-101.

[10] 李韶华，杨绍普. 一种非线性汽车悬架的亚谐共振及奇异性[J]. 振动工程学报,2007,20(2)：168-173. LI Shao-hua, YANG Shao-pu. Sub-harmonic resonance and singularity of a nonlinear vehicle suspension system[J]. Journal of Vibration Engineering,2007,20(2)：168-173.

[11] 金栋平，陈予恕. 滞后非线性系统的分岔和奇异性[J]. 天津大学学报,1997,30(3):299-304. JIN Dong-ping，CHEN Yu-shu. The bifurcations and singularities in systems with hysteretic nonlinearity [J]. Journal of Tianjin University, 1997,30(3):299-304.

[12] 苏密勇，谭永红，杨晓明. 一类具有迟滞-蠕变非线性对象的内模控制[J]. 吉林大学学报(工学版),2004,34(z1)：64-67. SHU Mi-yong，TAN Yong-hong，YANG Xiao-ming.Modeling and internal model control for systems with hysteresis and creep[J]. Journal of Jilin University(Engineering and Technology Edition),2004, 34(z1)64-67.

[13] Low T S, Guo W. Modeling of a three-layer piezoelectric bimorph beam with hysteresis[J]. Journal of Microelectromechanical Systems, 1995，4(4):230-237.

Principal resonance and singularity of a hysteretic nonlinear control system with a PID controller

XIONG Rui, LIU Xiang-dong

(College of Automation, Beijing Institute of Technology，Beijing 100081，China)

A hysteretic closed-loop nonlinear control system with a PID controller was studied. A model based on Backlash neutral network was adopted to approach the hysteretic nonlinear part of the system, the dynamic model of the system was established. The principal resonance of the system under a simple harmonic excitation was studied. The bifurcation equation of the system was obtained with the averaging method, and then the system’s singularity was analyzed completely, the transition sets and bifurcation plots were gained. The effects of the system’s parameters on its unfolding and bifurcation parameters were discussed. The results provided a theoretical guidance for selecting the system’s parameters.

hysteresis; nonlinear control system; Backlash neutral network model; principal resonance; singularity theory

北京市自然科学基金资助项目(4122066)

2012-12-28 修改稿收到日期：2013-04-19

熊蕊 女，博士生，1989年7月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2014.08.013