气隙偏心下永磁电机转子系统的振动特性分析

岳二团， 甘春标， 杨世锡

(浙江大学 机械工程学系 现代制造工程研究所，杭州 310027)

气隙偏心下永磁电机转子系统的振动特性分析

岳二团， 甘春标， 杨世锡

(浙江大学 机械工程学系 现代制造工程研究所，杭州 310027)

研究气隙偏心对永磁同步电机转子系统振动特性的影响。建立了气隙偏心下转子的动力学模型，结合永磁同步电机在带负载工作下转子永磁体及电枢电流共同形成的气隙磁场分布情况，利用Maxwell应力张量法计算了气隙偏心造成的不平衡磁拉力，并代入转子系统运动方程；通过实例分析，详细讨论了不同偏心以及负载类型对转子系统振动特性的影响。结果表明：质量偏心在增大转子振动的同时会削弱不平衡磁拉力的影响，使振动趋于规则；初始静偏心的大小和方向都将影响转子振动特性，当其方向和重力方向相反，振动强度将有所减弱；当外部负载转矩发生变化，其相应谐波频率的振动将被激发出来。

永磁电机；气隙偏心；不平衡磁拉力；负载转矩；振动特性

永磁同步电机采用永磁材料励磁，省去了励磁电源以及励磁绕组，具有结构轻便、运行可靠、效率高等特点，在各行业得到广泛应用。电机在运行时，由于受到机械力和电磁力的耦合作用，其振动情况复杂，特别是因加工精度及安装误差等原因导致定转子间气隙分布不均时，电机内部将产生不平衡电磁力，使电机轴承工作环境恶化，同时也使得转子振动更为剧烈，严重情况下甚至会导致转子和定子发生接触，使电机失效。针对气隙偏心时转子系统的振动问题，已有很多学者对传统电励磁电机做过研究，并取得许多好结果，而对于永磁电机，尤其是高性能的稀土永磁同步电机，这方面的文献则比较少[1]，其中部分文献简单引入电励磁电机的相关结论，而忽略了永磁电机本身的特点。

不平衡磁拉力(Unbalanced Magnet Pull, UMP)是转子振动分析时首先要研究的问题，在工程上往往采用线性公式[2]，即假设其大小与偏心率成正比，当偏心稍大时，这种方法误差较大。Kim等[3]对外转子永磁电机的偏心气隙磁场进行直接解析求解，得到气隙中各处的磁密分布，Kim等[4]运用该结果对转子表面的Maxwell应力进行积分得到磁拉力解析式，但其推导过程及结果过于复杂，使其应用受到限制，大大约束了该方法的应用。Guo等[5]通过将气隙磁导函数展开为级数形式，从而得到了不同极对数下三相同步电机空载时的不平衡磁拉力，进而分析了刚性支承转子系统的振动特性。在转子模型方面，目前的研究普遍采用单质量圆盘的两自由度转子模型，主要关注其横向振动，而且少有考虑不同负载对转子振动的影响，但实际上，外部负载是影响电机稳定性的一个重要因素。

本文在建立了两端柔性支承永磁同步电机转子模型的基础上，考虑初始静偏心及振动偏心同时存在的情况，推导了带负载运行时转子所受不平衡磁拉力，并通过实例分析，详细讨论了质量偏心、初始静偏心以及外部负载转矩变化对转子系统振动特性的影响。

1 系统动力学模型

本文采用如图1所示的转子模型。转子两端对称采用短轴承支承，Ob为轴承内圈中心，O1为圆盘中心，Oc为圆盘质心，Te为电磁转矩，T为外部负载转矩，δ为定转子间的气隙长度。

图1 转子系统模型Fig.1 A schematic of the rotor system

图2 气隙偏心下定转子几何结构Fig.2 Geometrical structure of the stator-rotor under air-gap eccentricity

当电机气隙偏心时δ将沿圆周方向变化，如图2所示，图中大圆为定子内圆面，小圆为转子外圆面，两圆之间即为气隙空间，C为转轴质心，δ0为名义气隙长度，r为工作中转子中心的偏移量，图中虚线为正常转子位置。考虑到转子半径远大于转子中心偏移量，故任意角度θ处的气隙长度可近似表达为

δ≈δ0-rcos(θ-γ)

(1)

(2)

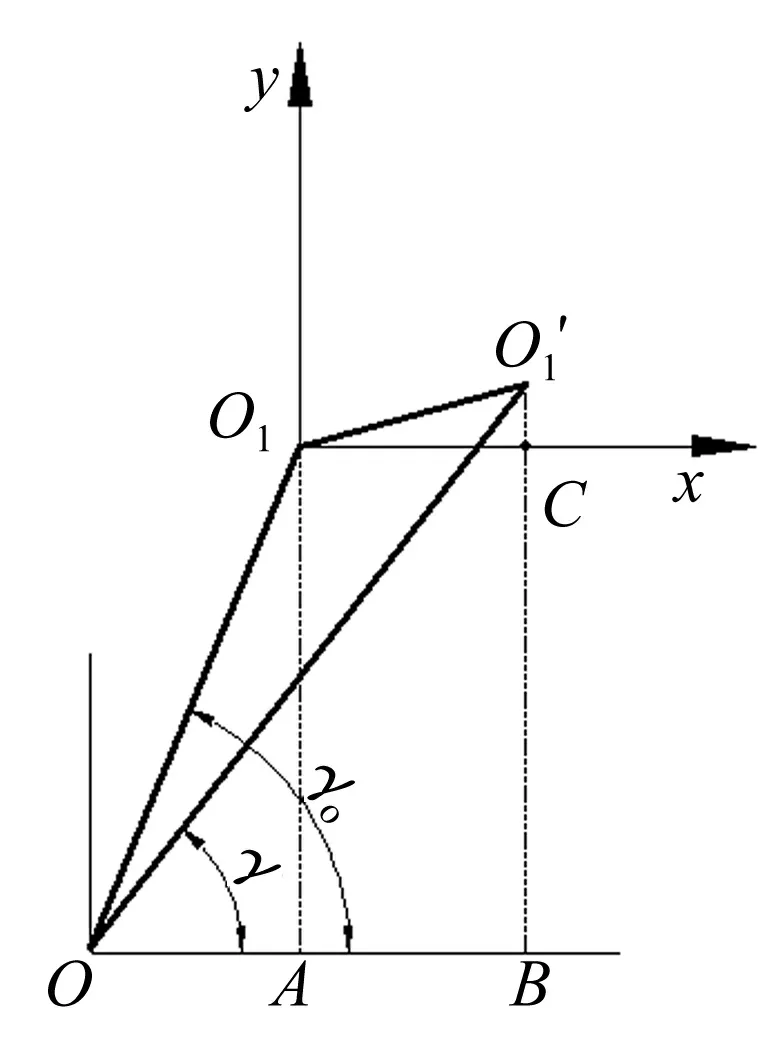
图3 转子中心偏移量计算模型Fig.3 A model of the eccentricity of rotor center

电机带负载运行时，转子系统除了受到外部转矩T和电磁转矩Te，同时还受滚动轴承支承反力Qb、不平衡磁拉力Fm和质量偏心力。由此，通过Lagrange方程可得转子运动方程为

(3)

式中，m为圆盘等效质量，m1为轴承端等效质量，a为圆盘质量偏心距，k,c,c1分别为转轴弹性系数、阻尼系数以及轴承处的阻尼系数，Te,T为电磁转矩及负载转矩，f为粘滞摩擦系数。由式(3)可知，转子的横向振动方程和转动方程存在耦合关系，为此，负载转矩的变化将影响到转子的横向振动。

以下分别对不平衡磁拉力Fmx、Fmy以及轴承支承反力Qbx、Qby进行分析。

1.1 不平衡磁拉力

为计算方便， 我们将电机气隙磁导Λ作如下处理[5]：

(4)

其中，S为每极气隙磁通面积，相对偏心ε=r/δ，系数Λn为

(5)

根据永磁同步电机运行相量图[6]，定子绕组及永磁转子的合成磁动势为

F(θ,t)=Fs+Fj=

Fsmcos(ωet-pθ)+

Fjmcos(pωrt-pθ-λ)

(6)

其中，Fsm为定子绕组磁势基波幅值，与绕组电流、匝数及绕线型式有关；Fjm为永磁转子向外提供的等效磁势幅值，与永磁体材料、外形尺寸及工作点有关；p为电机磁极对数，ωe为电角速度，ωr为转子旋转角速度，λ=(π/2+θN-φ)为定转子磁势夹角，其中θN、φ为转矩角及功率因数角。气隙中的磁密分布与径向Maxwell应力大小分别为

(7)

(8)

当偏心率较小时，式(4)中的级数项随阶次增加而迅速减小，故仅取其前四项代入式(8)，然后将σ在X,Y方向的分量分别沿转子表面进行积分，即可得到X,Y方向的不平衡磁拉力

(9)

其中

(10)

从式(9)和式(10)可以看出，不平衡磁拉力包含两部分：其中一部分(式(9)中第一项)和时间无关，仅与电枢磁势幅值、永磁磁势幅值及两者所夹的角度有关，方向指向最小气隙处；另一部分(式(9)中第二项和第三项)则随时间周期性变化，其幅值表达式中的磁导级数部分仅包含高阶系数乘积项Λ2,Λ3，故该部分幅值较前者小很多。

1.2 系统轴承力

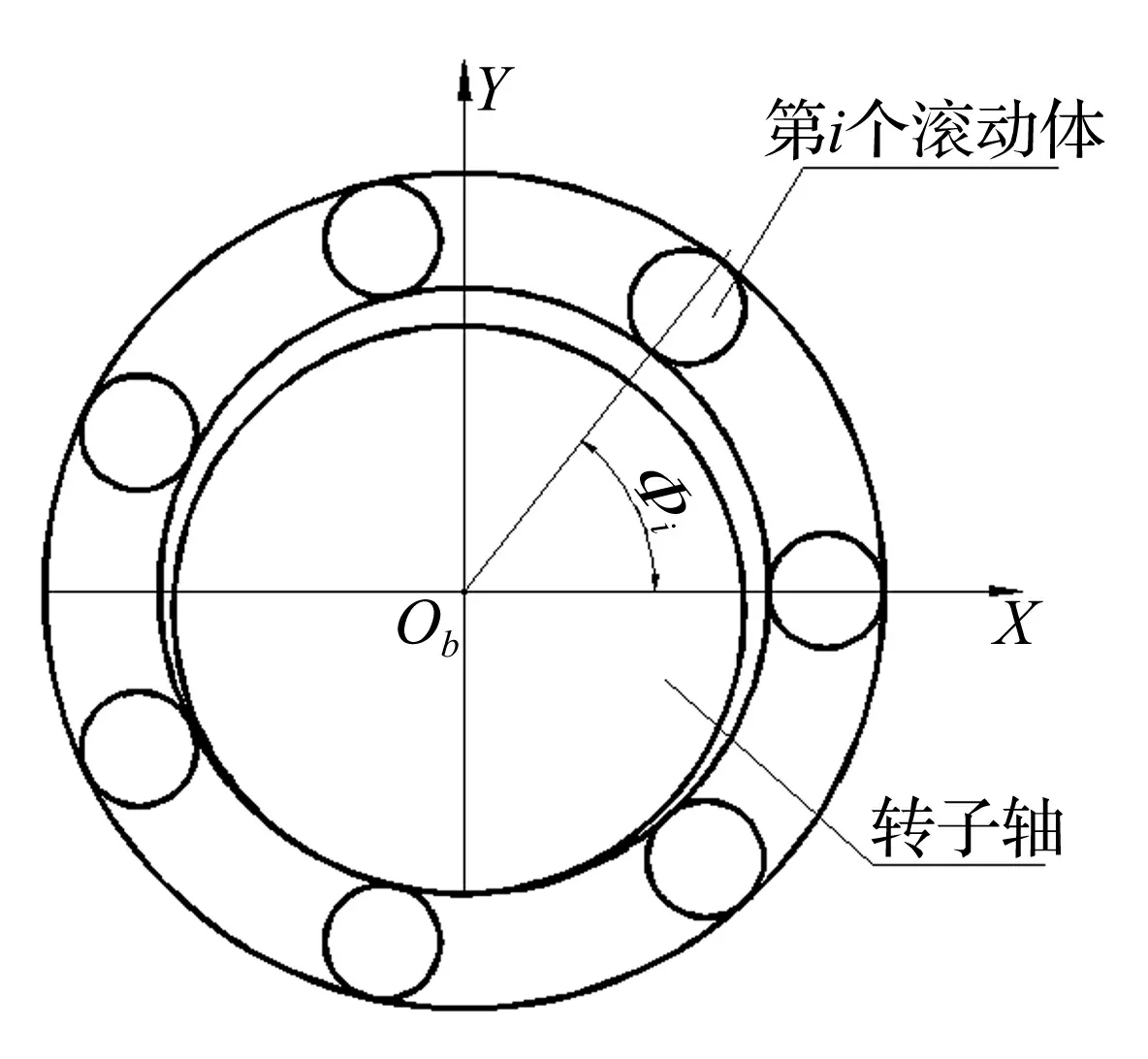
图4 滚动轴承示意图Fig.4 A schematic of the rolling bearing

本文选用深沟球轴承作为电机转子两端的支撑，轴承截面如图4所示。滚动轴承在工作过程中，受载荷的滚珠数量是不断变化的，故需讨论单个滚珠所提供的支承反力，然后再进行叠加。根据赫兹弹性接触理论，滚动体和内外圈滚道之间的接触变形载荷与接触变形量的关系为[7]

(11)

其中δi为第i个滚动体与滚道的接触弹性变形量，kb为总接触刚度。设x,y,α和λ分别为轴承内圈中心点在水平方向和垂直方向的位移、滚动轴承接触角和径向游隙，n为滚动体数目，φi为t时刻第i个滚动体的角位置，ωc和ω为滚动体公转角速度和转轴转动的角速度。

假设滚动体与滚道间只作纯滚动，则

(12)

式中下标“+”表示若结果为非负值则保留，若为负值则置零，因为此时该滚珠未受挤压。从而第i个滚动体所产生的回复力为

(13)

将各滚珠回复力叠加，即得滚动轴承的非线性轴承力为

2 实例分析

由于转子系统运动方程之间存在复杂耦合，难以求得解析解，故本文将通过数值仿真来研究转子振动特性。本文所选算例为一台额定功率7.5 kW、额定转速1 000 r/min的永磁同步电动机，采用龙格库塔法求解非线性振动微分方程。若无特别说明，均取：m=25 kg，m1=5 kg，J=0.093 4 kg·m2，c=200 N·s/m，c1=100 N·s/m，k=4.5×107N/m，R=82.5 mm，L=105 mm，δ0=3.0 mm，μ0=4×10-7H/m若不考虑偏心磁拉力等的影响，转子横向振动固有频率约为1 340 rad/s，远高于电机额定转速。

2.1 质量及初始位置偏心对转子系统振动的影响

由于转轴热处理工艺以及磁钢安装布置精度等原因，转子可能存在质量偏心，即转子质心和形心不重合，存在一个偏移量a。图5为永磁同步电机在额定负载下不同质量偏心时转子的轴心轨迹。由图5 (b)、(c)可见如果质量偏心量增大，振动幅值增加，而且轴心轨迹逐渐规则化，这是由于质量偏心的增加导致离心力增大，使得离心力在各影响因素中占主导作用，电磁力的影响则明显减弱。

图6为当电机存在初始静偏心时转子的轴心轨迹。由图6 (b)、(c)可见，初始静偏心的存在将使转轴整体朝最小静偏心方向偏移。一般情况下，转子振幅会随静偏心增大而增大，但在静偏心角靠近π/2时，振动有所缓和，因为此时静偏心造成的气隙不均和重力引起的转轴偏移会相互削弱。类似地，当静偏心角与重力方向接近时，会使转子振动大幅增加。由式(9)可得各静偏心情形下Y方向的不平衡磁拉力，见图7，计算结果表明，当静偏心方向与重力方向相反时，不平衡磁拉力将被削弱。

因此，初始静偏心对转子振动有较大影响，尤其是水平放置的电机，若安装时使转轴朝重力方向偏移，将会大大增加转子的振动。

图5 不同质量偏心时转子轴心轨迹(其中r0=0.1 mm，γ0=π/4) Fig.5 Rotor center locus with different mass eccentricities

图6 不同静偏心下转子轴心轨迹Fig.6 Rotor center locus with different static eccentricities

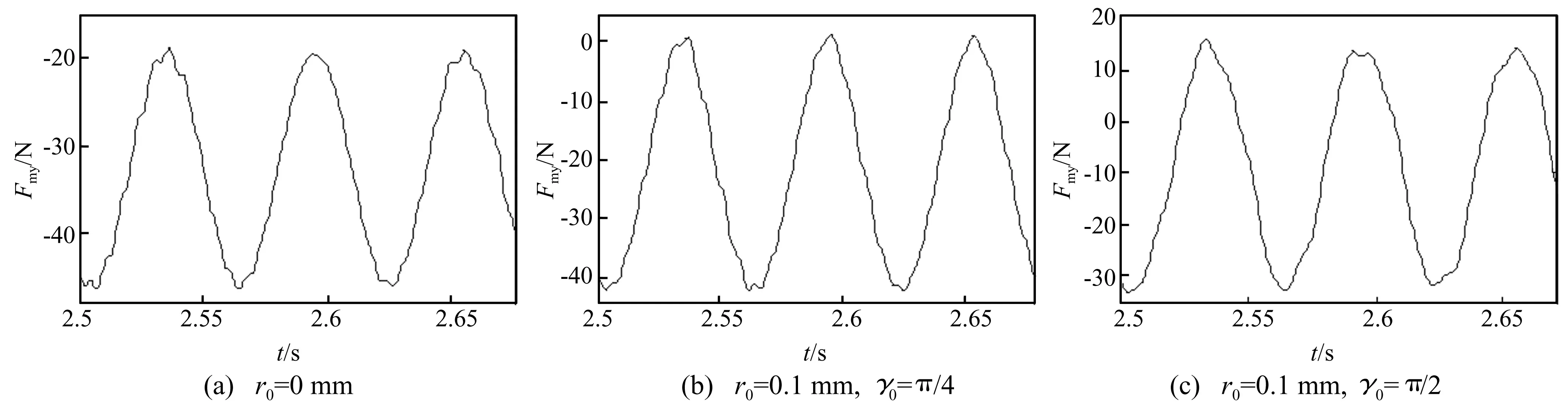
图7 不同静偏心下Y方向的不平衡磁拉力 Fig.7 Unbalanced magnet pull on Y direction with different static eccentricities

2.2 负载变化对转子系统振动的影响

前述假定所研究的永磁同步电机工作在额定状态下，即在恒定的额定负载转矩TN下以额定转速运转。然而在许多工程应用中，负载转矩受外界扰动将发生变化，从而将引起电枢电流以及气隙磁场的变化。下面进一步分析两种不同形式的负载变化对转子系统振动响应的影响。

考虑到不同应用需求以及不同控制策略，本文作以下假设：当负载转矩变化时，电机通过调节其电枢电流以及定转子磁势夹角，以快速跟踪转矩变化；在电源电压和电机转速基本恒定时，电枢电流的变化与负载转矩变化呈线性关系。

首先，设负载转矩按正弦规律变化，即T=TNsin2πft，其幅值TN=71 N·m，频率f=10 Hz，代入系统动力学方程(3)后可解得转子在Y方向的振动，见图8。

图8 正弦负载下转子振动信号Fig.8 Vibration of rotor under sine load

由图8可见，信号频率较恒定负载下丰富，主要的频率成分有：由转子自身重力和初始位置偏心共同引起的相对固定的成分(0 Hz)、转轴旋转引起的转速成分(16.7 Hz)、负载频率成分(10 Hz)以及2倍负载频率成分(20 Hz)。因此，负载转矩的频率及其2倍频可在转子振动信号中体现出来。

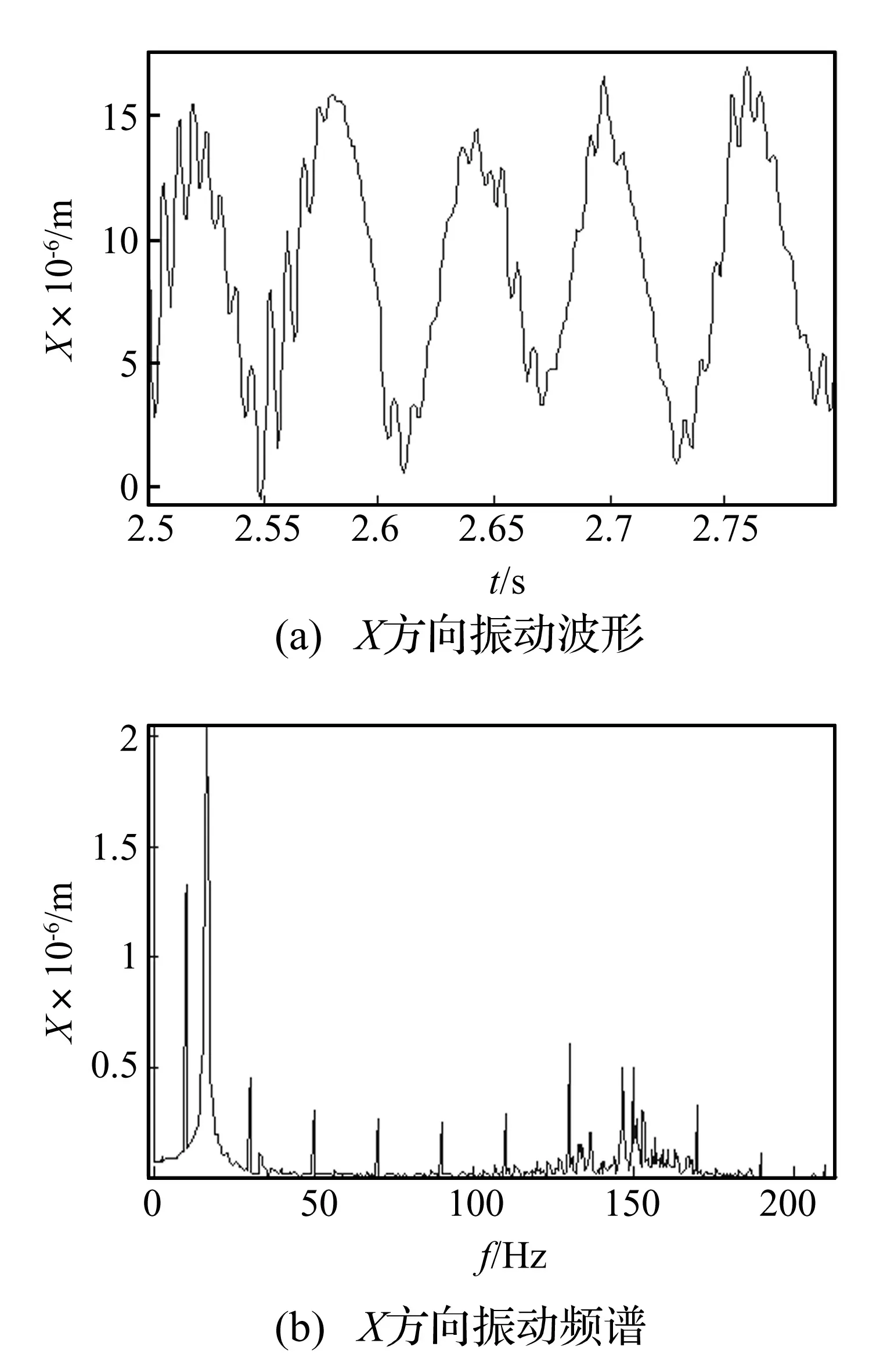
图9 负载转矩周期方波变化时转子振动图线Fig.9 Vibration of rotor under periodical square load

进而，设方波负载幅值为71 N·m，频率为10 Hz，占空比为0.5。类似前述方法，可得负载转矩作方波形变化时的振动信号，见图9。由图9可见，此时转子振动情况变得复杂，多种高频成分的信号被激发出来：除了重力和初始偏心造成的固定偏移成分(0 Hz)、转速频率成分(16.7 Hz)、负载频率成分(10 Hz)，负载转矩的奇数倍频也被激发出来，而且有多个高频成分集中于150 Hz附近。这是因为，周期性方波信号可通过傅里叶级数分解为不同正弦函数的和，而这些正弦函数的频率恰好分别为基频的奇数倍，因而方波型负载转矩可看作由多种谐波成分组成，在作用到永磁同步电机转子上后，各谐波频率将被激发出来。

3 结 论

本文针对永磁同步电机气隙偏心问题，首先建立了柔性支承的转子系统模型，分析了电机在带负载工作时气隙磁场分布以及不平衡磁拉力，进而通过数值仿真，详细分析了不同偏心情形以及不同负载类型时转子系统的振动响应，得到了如下结论：

(1) 质量偏心较小时，不平衡磁拉力对转子振动的影响比较显著，随着质量偏心的增大，转子振幅有所增加，同时电磁力的影响被弱化；

(2) 初始静偏心的存在对转子系统振动有重要影响。当静偏心方向与重力方向相同或相近时，转子振动将得到加强，而当静偏心与重力方向相反时，由于二者的作用相互削弱，故转子振动有所减弱；

(3) 考虑外部负载的作用将能更准确描述电机转子系统的振动特性，当负载转矩发生变化时，其所含谐波成分的频率将在转子振动信号中体现出来。

[ 1 ] Ebrahimi B M, Faiz J, Roshtkhari M J. Static, dynamic, and mixed eccentricity fault diagnoses in permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2009, 56(11): 4727-4739.

[ 2 ] 王天煜. 高速永磁电机转子综合设计方法及动力学特性的研究[D]. 沈阳：沈阳工业大学, 2010.

[ 3 ] Kim U, Lieu D K. Magnetic field calculation in permanent magnet motors with rotor eccentricity: without slotting effect[J]. IEEE Transactions on Magnetics, 1998, 34(4): 2243-2252.

[ 4 ] Kim T J, Hwang S M, Park N G. Analysis of vibration for permanent magnet motors considering mechanical and magnetic couple effects[J]. IEEE Transactions on Magnetics, 2000, 36(4): 1346-1350.

[ 5 ] Guo D, Chu F, Chen D. The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor[J]. Journal of Sound and Vibration, 2002,254(2): 297-312.

[ 6 ] 刘锦波，张承慧，等. 电机与拖动[M]. 北京：清华大学出版社，2006.

[ 7 ] 王彦生，张耀强，张彦斌，等. 非线性Jeffcott转子-滚动轴承系统动力学分析[J]. 振动、测试与诊断，2010,30(4)：367-371. WANG Yan-sheng, ZHANG Yao-qiang, ZHANG Yan-bin, et al. Dynamics analysis of a nonlinear rolling bearing-Jeffcott rotor system[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(4): 367-371.

[ 8 ] Dorrell D G, Hsieh M F, Guo Y G. Unbalanced magnet pull in large brushless rare-earth permanent magnet motors with rotor eccentricity[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4586-4589.

[ 9 ] Wang Y F, Huang L H, Li Y. Nonlinear vibration and stability of a jeffcott rotor under unbalanced magnetic excitation[J]. International Journal of Nonlinear Science and Numerical Simulation, 2007, 8(3): 375-384.

[10] Wu B S, Sun W P, Li Z G, et al. Circular whirling and stability due to unbalanced magnetic pull and eccentric force[J]. Journal of Sound and Vibration, 2011, 330(21): 4949-4954.

[11] Im H, Yoo H H, Chung J. Dynamic analysis of a BLDC motor with mechanical and electromagnetic interaction due to air gap variation[J]. Journal of Sound and Vibration, 2011, 330(8): 1680-1691.

[12] Lubin T, Mezani S, Rezzoug A. Two-dimensional analytical calculation of magnetic field and electromagnetic torque for surface-inset permanent magnet motors[J]. IEEE Transactions on Magnetics, 2012, 48(6): 2080-2091.

[13] 王天煜，王凤祥，方程. 高速永磁电机机组轴系振动研究[J]. 振动与冲击, 2011, 30(9): 111-115. WANG Tian-yu, WANG Feng-xiang, FANG Cheng. Vibration analysis of shafting of high speed permanent magnetic machinery[J]. Journal of Vibration and Shock. 2011, 30(9): 111-115.

[14] 林利红，陈小安，周伟，等. 永磁交流伺服精密驱动系统几点耦合振动特性分析[J]. 振动与冲击，2010,29(4)：48-53. LIN Li-hong, CHEN Xiao-an, ZHOU Wei, et al. Electromechanical coupled vibration characteristic analysis for a permanent magnet AC servo precision drive system[J]. Journal of Vibration and Shock, 2010, 29(4): 48-53.

[15] 郭丹, 何永勇, 褚福磊. 不平衡磁拉力及对偏心转子系统振动的影响[J]. 工程力学, 2003,20(2): 116-120. GUO Dan, HE Yong-yong, CHU Fu-lei. The calculation of unbalanced magnetic pull and its effect on vibration of an eccentric rotor[J]. Engineering Mechanics, 2003,20(2): 116-121.

[16] 唐任远. 现代永磁电机:理论与设计[M]. 北京：机械工业出版社, 1997.

Vibration characteristics analysis of a rotor for a permanent magnet motor with Air-Gap Eccentricity

YUE Er-tuan, GAN Chun-biao, YANG Shi-xi

(Department of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China)

The vibration characteristics of a rotor system of a permanent magnet synchronous motor with air-gap eccentricity were studied. The dynamic model of the rotor system was built. According to the distribution of magnetic flux density generated by permanent magnet and the armature current under loaded, the unbalanced magnet pull (UMP) was calculated with Maxwell stress tensor method and it was substituted into the dynamic model. Through several illustrating numerical examples, the effects of different eccentricities and loads on the rotor vibration were discussed in detail. The results showed that the mass unbalance weakens the effect of the UMP and aggravates the vibration of the rotor; the magnitude and orientation of initial eccentricity can also change the vibration characteristics of the rotor, and the vibration is weakened when the orientation of initial eccentricity is opposite to that of gravity; as the load torque changes, the corresponding vibration components are excited with the same harmonic frequencies as those of the load.

permanent magnet motor; air-gap eccentricity; unbalanced magnet pull; load torque; vibration characteristics

国家自然科学基金(11172260,11072213)；高等学校博士学科点专项科研基金(20110101110016)

2013-03-13 修改稿收到日期：2013-06-03

岳二团 男，硕士生，1986年生

甘春标 男，教授，1971年生

TH113

A

10.13465/j.cnki.jvs.2014.08.006