基于椭圆曲线的数字签名快速算法研究

2014-08-10吴婷婷

实验科学与技术 2014年6期

关键词：数字签名椭圆消息

张贺，孙旭，吴婷婷

(成都理工大学信息科学与技术学院，成都 610059)

·计算机及网络技术应用·

基于椭圆曲线的数字签名快速算法研究

张贺，孙旭，吴婷婷

(成都理工大学信息科学与技术学院，成都 610059)

椭圆曲线密码；数字签名；快速验证

数字签名技术是电子商务和安全认证的重要技术之一，主要用于防止伪造、抵赖、冒充和篡改等安全问题，可以保证数据在网络传输过程中的完整性和不可否认性[1]。目前使用的数字签名算法主要有整数因子分解算法(RSA)、离散对数算法(DSA)、椭圆曲线离散对数算法(ECDSA)等。

Koblitz[2]和Miller[3]在1985年提出了椭圆曲线密码体制,它可以使用较短的密钥获得较高的安全性，使用比RSA短得多的密钥就可以达到相同的安全系数，在运算能力、存储量、带宽和软硬件条件受限的情况下，椭圆曲线密码体制更容易实现，并具有更高的安全性。例如，椭圆曲线算法使用160 bit密钥就可以实现RSA算法使用1 024 bit密钥提供的安全性[4]。

椭圆曲线数字签名算法是数字签名算法的椭圆曲线版本。最广泛、标准化的椭圆曲线数字签名包括ANSI X9.62、FIPS186-2、IEEE1363-2000和ISO/IEC15946-2标准，以及一些标准的草案[5]。国内外学者研究的重点倾向于如何获得更高的计算效率。本文从签名和验证算法方案的角度研究如何提高计算效率，并使用软件进行验证。

1 椭圆曲线密码体制

椭圆曲线密码体制使用的是变元和系数均为有限域中元素的椭圆曲线。密码应用中所使用的两类椭圆曲线是定义在GF(p)上的素曲线和在GF(2m)上构造的二元曲线[6]。其中，GF(p)上的椭圆曲线更适合加密、更容易软件实现[7]，因此，主要介绍素域的椭圆曲线密码。

对于GF(p)上的椭圆曲线，其变元和系数均在GF(p)里取值，方程形式如下：

y2modp=(x3+ax+b)modp

式中：p是一个大素数；a、b是两个小于p的非负整数，满足条件：

(4a3+27b2)modp≠0modp

Ep(a,b)表示素域上的椭圆曲线群，是指素域上方程的解集和一个无穷远点O构成的点集。对椭圆曲线上任意点P,Q∈Ep(a,b)有：

1)P+O=P，O为加法单位元；

2)如果P=(xp,yp)，则点(xp,-yp)是P的负元，记为-P；

3)点加。若有点P=(x1,y1)和点Q=(x2,y2)，且P≠-Q，则有点R=(x3,y3)使R=P+Q，其中，

4)点乘或倍乘。点p=(x1,y1)，p≠-p，则2p=(x3,y3)，其中，

2 椭圆曲线数字签名算法

2.1 数字签名概述

普通的物理签名代表着一个人的身份和所获得的权限。普通的物理签名可通过模仿笔迹伪造签名，而数字签名则是只有信息发送者才能产生，别人不可伪造的消息摘要，数字签名的大概流程如图1所示。

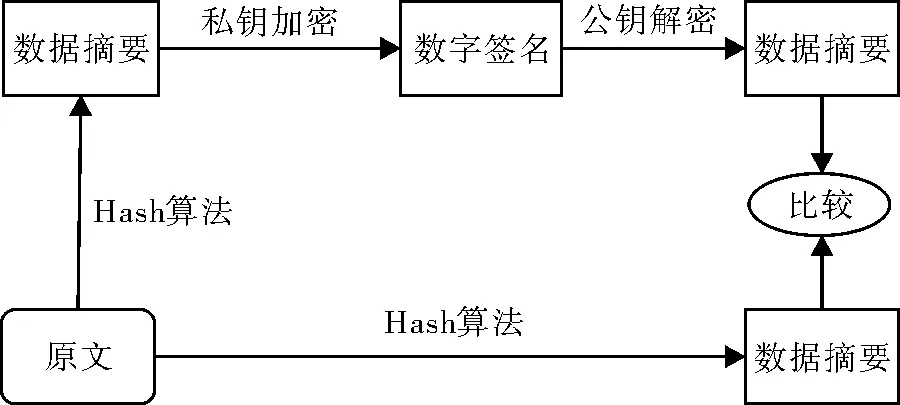
图1 数字签名流程

1)签名过程。(1)发送者将原文通过Hash算法计算得到数据摘要，将数据摘要加密得到数字签名；(2)将获得的签名和原文一起发送给接受者。

2)验证过程。(1)将接收到的签名用相应的公钥解密得到数据摘要；(2)接收的原文通过Hash算法计算得到数据摘要，如果两个摘要相同，则验证成功，否则验证失败。

要保证实际应用的安全，数字签名还必须满足以下条件：

1)防止伪造性。数字签名可以使接受者确定发送者的身份从而确定消息的正确性。

2)数据完整性。数字签名是通过将要发送的消息进行运算形成消息摘要而获得的，接受方可以通过验证判断消息是否在传输过程中被修改，从而保证消息的完整性。

3)不可抵赖性。数字签名可以证明消息的来源，接受方可以判断出消息发送者从而防止发送方的抵赖行为。

4)如果收发双方对数字签名的真假存在异议，则有可靠第三方(如CA)协调解决。

2.2 椭圆曲线数字签名算法

目前，数字签名中使用较为广泛的公钥加密体制是RSA算法，然而，随着计算机运算能力的快速提升，RSA算法越来越不能满足数字签名安全度的要求。椭圆曲线密码算法的密钥短、速度快、适用于软硬件受限的情况，因此，椭圆曲线密码算法在数字签名中应用越来越广泛。基于椭圆曲线密码体制的数字签名算法是椭圆曲线数字签名算法(ECDSA)[8]。

ECDSA主域参数有：

D=(q,FR,a,b,G,n,h)

1)选择素数域GF(p)，q=p；

2)一个域表示法FR来表示域中的元素；

3)a和b表示GF(p)域中的两个元素；

4)G为椭圆曲线上的基点，用域上的xG和yG两个元素来定义；

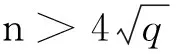
6)余因子h。

另外，还有消息摘要算法哈希函数SHA-1或SHA-256。

令椭圆曲线的基点为G(x1,y1)时，椭圆曲线数字签名的算法如下[9]：

1)生成签名算法

(1)选择随机数或伪随机数k∈[1,n-1]；

(2)计算R=kG(x1,y1)，得到R横坐标为X；

(3)计算r=Xmodn，如果r=0，则返回1；

(4)计算k-1modn；

(5)e=SHA-1(m)，m为所发送的消息；

(6)计算s=k-1(e+dr)modn，如果s=0，则返回1；

(7)对消息的签名为(r,s)，将(r,s,m)发送给接收方。

2)接收方接收到签名和消息后，验证算法

(1)验证r和s是[1,n-1]内的整数；

(2)计算e=SHA-1(m);

(3)计算w=s-1modn;

(4)计算u1=ewmodn，u2=rwmodn；

(5)计算R=u1G+u2Q；

(6)如果R=0，验证失败，否则，R=(X1,Y1)，计算v=X1modn；

(7)如果v=r，验证成功。

3 椭圆曲线快速数字签名算法

3.1 改进的椭圆曲线数字签名

ECDSA一般是用(s,e,r)去置换签名方程xk=y+dzmodn中的(x,y,z)，得到sk=e+drmodn，从而计算出s，形成签名信息(r,s)。改进算法用(1,s+e+r,1)去置换签名方程，得到s=k-e-r-d。则改进的快速数字签名算法步骤如下：[10]

1)从椭圆曲线上获得主域参数

D=(q,FR,a,b,G,n,h)

2)签名过程

(1)选择一个随机数k∈[1,n-1];

(2)计算kG=(X1,Y1)，r=X1modn，如果r=0，返回1；

(3)计算e=SHA-1(m)，m为明文；

(4)计算s=k-e-r-d，如果s=0，则返回1；

(5)传送消息m和签名(r,s)。

3)验证过程

(1)验证r和s是[1,n-1]内的整数；

(2)计算e=SHA-1(m)；

(3)计算w=s+e+rmodn;

(4)计算R=wG+Q=kG=(X1,Y1)，如果R=0，则签名无效；否则，计算v=X1modn；

(5)如果v=r，则接受签名；否则，签名无效。

3.2 改进算法分析

3.2.1 改进的签名算法正确性分析

签名方程：

k=s+e+r+dmodn

s=k-e-r-d

对应的验证方程：

R= (s+e+r)G+Q=

(k-e-r-d+e+r)G+dG=

(k-d)G+dG=kG

因此，改进的签名算法可以正确完成签名和验证过程。

3.2.2 改进算法耗时分析

在ECDSA算法中，主要耗时是模乘、模逆和标量乘，本文分别用[M]、[I]和[S]表示，其他的加减运算可以忽略不计。在文献[11]中，分析了三种运算的耗时比例，可以得到[I]=9[M]和[S]≈173[M]+75[I]=848[M]。

经典ECDSA算法在签名过程进行了1次模乘、2次模逆和1次标量乘，则耗时为N1=[M]+18[M]+848[M]=867[M]；在验证过程进行了1次模逆、2次模乘和2次标量乘，则耗时为N2=1 696[M]+2[M]+9[M]=1 707[M]，总共耗时为N=N1+N2=2 564[M]。

改进ECDSA算法在签名过程仅进行了1次标量乘，与经典ECDSA算法相比避免了模乘和模逆，耗时为N1=848[M]；在验证过程也只进行了1次标量乘，同样避免了模乘和模逆，耗时为N2=848[M],总耗时为N=1 696[M]。

3.3 改进的数字签名的验证实现

为了比较两种算法实际耗时，可以利用软件进行测试。椭圆曲线数字签名算法的软件实现已经成熟，在Windows平台下能够友好地显示用户界面，使用vs2008运行完整的软件，根据改进的数字签名算法过程，使用C++语言编写快速数字签名的签名和验证过程代码，替换到软件代码中，并利用clock()函数分别获得签名过程和验证过程的程序执行时间。改进的数字签名算法的关键代码如下：

1)签名过程

Point P;BigInteger k,temp1(1); L:srand(unsigned(GetTickCount())); k=temp1+Rand(n-temp1);

P=G;P=Point_Multiply(G,k);

s=k-e-r-d;

if(Compare(s)){goto L;}

2)验证过程

BigInteger temp1(1);

if(Compare(r,n-temp1)||Compare(s,n-temp1))

{return false;}

if(Compare(w)){return false;}

Point R,R1;

R1=Point_Multiply(G,w);

R=Point_Calculate(R1,Q);

if(Compare(R.x)&&Compare(R.y))

{return false;}

if(Compare(v,r)){return false;}

return ture；软件在搭载intel酷睿双核、主频为2.1 GHz的处理器T6500的计算机上运行结果如图2所示。首先，生成椭圆曲线的主域参数D=(q,FR,a,b,G,n,h)；然后，生成公钥Q和私钥d；最后进行签名和验证并得到签名和验证的时间共0.098 s。

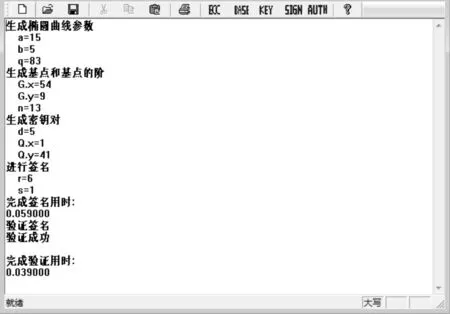
图2 改进后软件测试结果

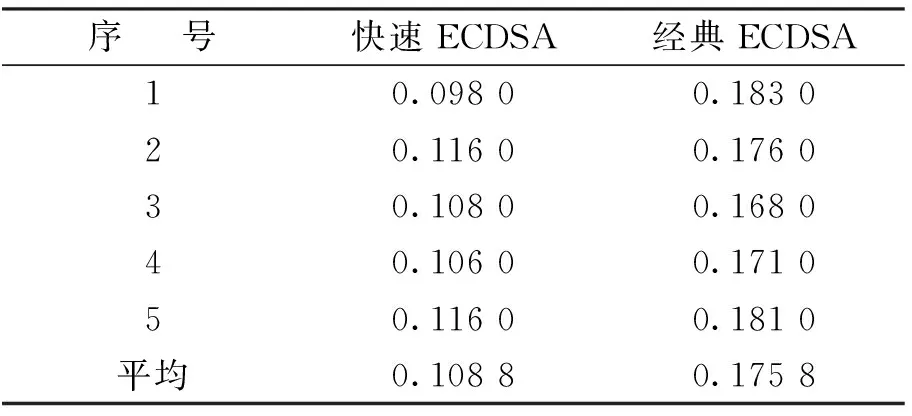
表1 算法程序执行的时间比较 s

4 结束语

[1]赵泽茂.数字签名理论[M].北京:科技出版社,2007:23-45.

[2] Koblitz N. Elliptic curve cryptosystems[J]. Mathematics of Computation,1987,48(177):203-209.

[3] Miller V. Uses of elliptic curves in crytography[C]//Advances in Cryptology-CRYPTO'85,LNCS218. Santa Barbara, Calif:Springer-Verlag, 1986:417-426.

[4] 王晖，张方国，王育民. 大素数域上椭圆曲线密码体制的软件实现[J]. 西安电子科技大学学报：自然科学版,2002，29(3):426-428.

[5] 蔡永泉.数字鉴别与认证[M].北京：北京航空航天大学出版社, 2011.

[6] William Stallings.密码编码学与网络安全——原理与实践[M].5版.北京：电子工业出版社，2012:222-223.

[7] 张鹏.ECC椭圆曲线加密算法在软件注册中的应用[D].太原：太原理工大学，2010:43-45.

[8] 张岩.基于椭圆曲线的数字签名算法研究[D].成都：西南交通大学,2010:25-26.

[9] 罗涛,易波.关于椭圆曲线数字签名算法研究[J].计算机工程与应用,2003(29):184-187.

[10] 陈亮,椭圆曲线数字签名算法的优化和软件实现[D].杭州：杭州电子科技大学,2011:34-37.

Research of Digital Signature Algorithm Based on Elliptic Curve

ZHANG He，SUN Xu，WU Tingting

(College of Information Science and Technology，Chengdu University of Technology，Chengdu 610059，China)

elliptic curve code；digital signature；fast verification

2013-10-15