基于COMSOL Multiphysics的通电螺线管磁场分析

王慧娟，李慧奇

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

基于COMSOL Multiphysics的通电螺线管磁场分析

王慧娟，李慧奇

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

文中通过载流螺线管模型，分析了有限长螺线管磁感应强度的理论算法，并用仿真软件COMSOL Multiphysics 建模并仿真，得到了螺线管模型磁感应强度的三维立体解，形象直观地表现了螺线管空间磁场的分布情况。同时，验证了与理论计算结果的一致性，并为电磁场其他问题的仿真建模提供参考。

螺线管；磁感应强度；COMSOL Multiphysics软件；仿真

通电有限长密绕螺线管磁场测量实验是电磁场的经典实验之一，由于该实验只能测量、计算螺线管轴线上的磁场，不能反映整个螺线管内部的磁场分布情况，对此，已有一些文献从理论上做过研究[1-5]，有些文献给出了形式解[1-2]，有些从数值上近似计算出定积分[3-4]，只是结果不够形象直观。COMSOL Multiphysics 是一款基于有限元法的多物理场的大型数值仿真软件，其中的AC/DC模块是电磁场模块，可以模拟准静态电磁场的相关物理问题，由于其强大的多物理场耦合功能，应用越来越广泛。

1 理论分析

1.1 螺线管轴线磁场推导

一个轴向长度为2L,半径为a，单位长度匝数为n的螺线管界面图如图1所示，z轴为对称轴，由于匝数比较多，所以通过每匝的电流i基本是沿φ方向的，可等效为面电流。我们只求z轴上的B,

电流密度如式(1)所示：

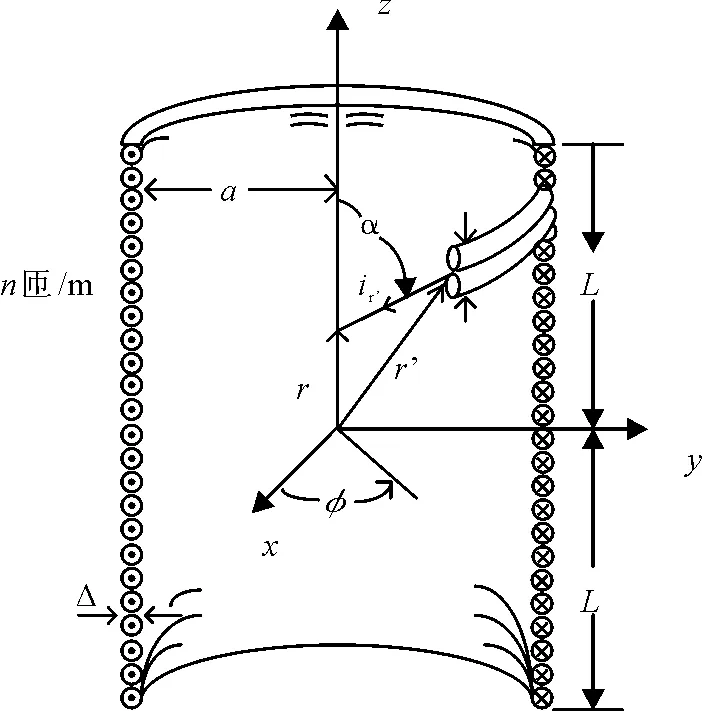
图1 螺线管模型

(1)

根据毕奥-萨伐尔定律[7]，有

(2)

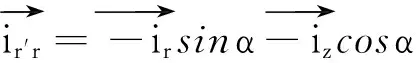
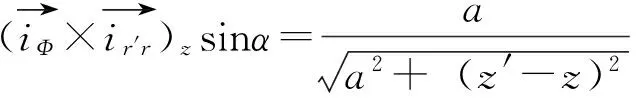
代入式(2)得到

(3)

利用替代关系z″=z′-z得到

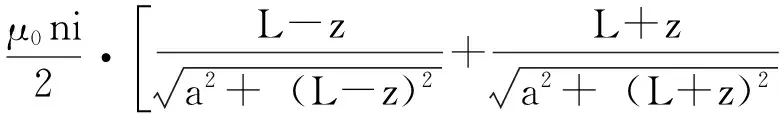
(4)

对于有限长螺线管，沿轴的内部场用B∞表示，在z轴上z≪L处(代表螺线管中部区域)，式(4)可化简为:

(5)

在螺线管长度远远大于它的半径的极限下，即：L≫a，这个表达式成为:

(6)

在螺线管的口上，即：z=±L处，式(4)可以简化为：

(7)

1.2 螺线管空间任意一点磁场

根据文献[4],对单匝圆环电流在空间任意一点的磁感应强度进行积分，可得到多匝圆环电流即螺线管空间任意点的磁感应强度，其表达式为：

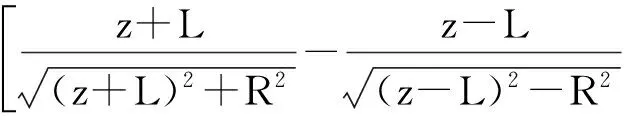
(8)

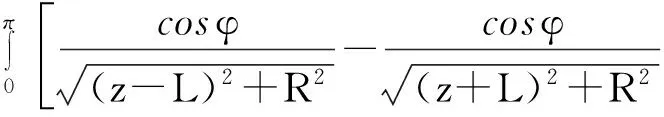
(9)

(10)

其中，R2=a2+ρ2-2aρcosφ

当位于螺线管轴线上时，ρ=0，R2=a2，此时

(11)

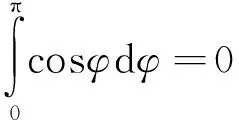
(12)

与前文所述一致。

2 建模仿真

2.1 理论值分析

在通电螺线管磁感应强度的测量实验中，采用的螺线管模型长度为28 cm，平均半径2 cm，导线2 800匝，所通电流为直流1 A，该实验利用霍尔效应，测得螺线管中部区域磁感应强度约为0.012 T，端口处约为0.006 T。现对该模型的理论值进行分析，根据式(6)，计算得到该螺线管内部的磁感应强度为：

根据式(7)，螺线管端口处的磁感应强度为：

可见，理论值与实验测量值近似相等。

2.2 仿真

用软件COMSOL Multiphysics建立螺线管仿真模型。该模型利用螺线管圆环电流的轴对称特性，建立横截面为1.2 cm×28 cm的矩形载流导体，其中心距对称轴2 cm，分别代表螺线管的厚度为1.2 cm，长度为28 cm，平均半径为2 cm。材料选为铜线，在矩形横截面上加多匝电流，则计算得到的螺线管内部空间的磁感应强度的三维剖面图如图2所示，沿直径的二维剖面磁感应强度线示意图如图3所示，在中心轴线上的磁感应强度如图4所示。

可见，在轴线上的磁感应强度为0.012 T，在端口处约为0.06 T，仿真结果与理论计算值近似相等。误差主要由于该模型没有考虑线圈之间的间隙，近似为面电流。该模型能直观地反映出螺线管内部空间的磁场分布情况，即中部区域磁感应强度近似均匀分布，快到端口处时变化较大，端口处的磁感应强度为中部的二分之一。由图3可见，螺线管外部区域的磁场并不为零，只是值比较小，近似为零。磁力线类似于磁偶极子。

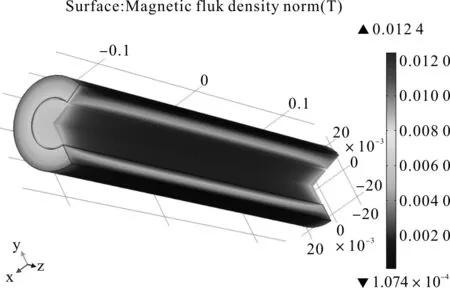
图2 螺线管磁感应强度三维剖面图

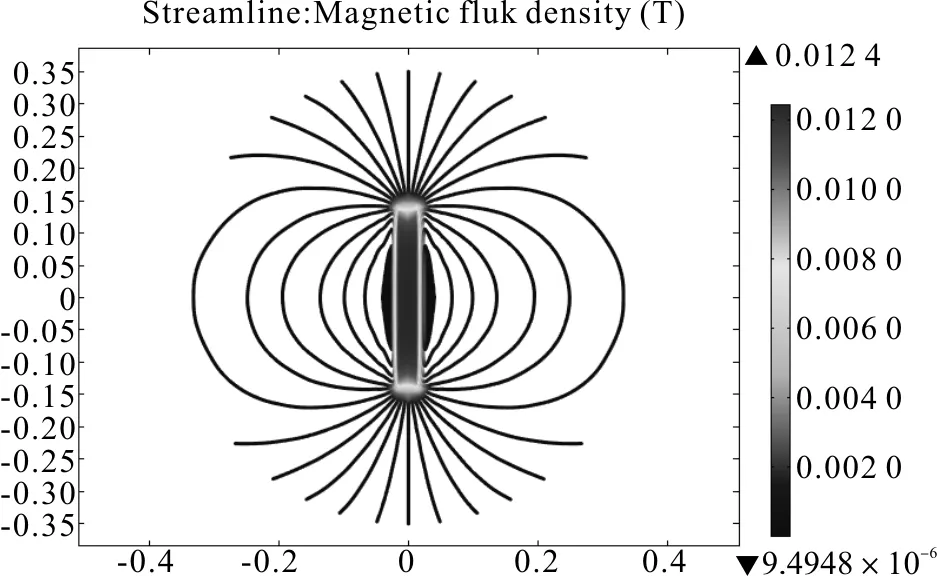
图3 磁通密度线分布

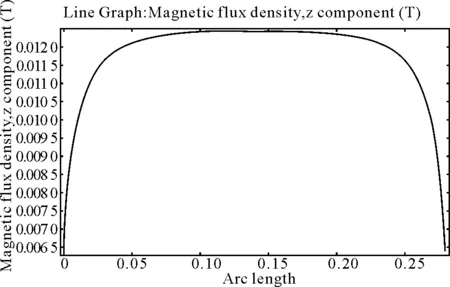
图4 轴线上磁感应强度

3 结束语

本文总结了有限长螺线管磁感应强度的理论算法，得到了包括轴线磁感应强度的解析表达式和空间磁感应强度的积分表达式。然后，用仿真软件COMSOL 建模并仿真，得到了螺线管模型磁感应强度的三维立体解，形象直观地表现了螺线管空间磁场的分布情况，同时，验证了与理论计算结果的一致性，并为电磁场其他问题的仿真建模提供参考。

[1]惠小强, 陈文学. 有限长通电螺线管空间的磁场分布[J]. 物理与工程, 2004, 14(2): 22-23.

[2] 陈红, 侯国栋. 长直螺线管的电磁场分析与仿真[J].郑州轻工业学院学报: 自然科学版, 2013(1): 100-104.

[3] 赵春旺, 王克勋. 有限长螺线管磁场的数值计算与分析[J]. 工科物理, 1997(4): 14-17.

[4] 刘耀康. 螺线管磁场的数值解[J]. 高师理科学刊, 2008, 28(1): 60-64.

[5] 常同钦. 截面为任意形状无限长螺线管的磁场[J]. 大学物理, 2001(6): 22-23.

[6] Haus H A，Melcher J R.电磁场与电磁能[M].江家麟，周佩臼，钱秀英，等译.北京：高等教育出版社，1992:263.

Analysis of the Magnetic Field in Solenoid Based on COMSOL Multiphysics

WANG Huijuan, LI Huiqi

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

Based on the solenoid model, this paper analyzes the theoretical algorithm of the magnetic induction in finite length solenoid, then the modeling and simulation is carried out on using the software COMSOL Multiphysics, the three-dimensional results of the solenoid magnetic induction has been calculated. The solution visualizes the performance of spatial distribution of the magnetic field in the solenoid. The result has also been compared with the theoretical calculations, the consistency is verified. This paper also provides a reference for other electromagnetic simulations.

solenoid; magnetic induction; COMSOL Multiphysics software; simulation

2014-02-24

王慧娟(1981-)，女，硕士，工程师，研究方向：电力系统电磁兼容。

TM12

A

10.3969/j.issn.1672-4550.2014.06.011