子野分割算法对剂量分布和计划执行效率的影响
2014-08-10李金凯李彩虹王沛沛孙新臣
李金凯,李彩虹,王沛沛,孙新臣
(南京医科大学第一附属医院 放疗中心,南京210029)
子野分割算法对剂量分布和计划执行效率的影响
李金凯,李彩虹,王沛沛,孙新臣
(南京医科大学第一附属医院 放疗中心,南京210029)
目的:比较Elekta XIO TPS (版本:4.70)2种子野分割算法分别为SLD和SMT对剂量分布和计划执行效率的影响。方法:选取9例鼻咽癌患者进行调强计划逆向优化生成射野通量分布图,改变子野分割算法的有关参数产生不同的子野序列。SLD算法,最小子野边长取1cm、2cm、3cm产生3组子野序列,强度分层等级取6、8、10、12、15产生5组子野序列;SMT算法,最小子野面积取2cm2、4cm2、6cm2产生3组子野序列,子野抑制因子取3、5、7产生3组子野序列。对14组子野序列计算得到的剂量分布进行相关剂量学参数的对比分析,考虑机器跳数及子野总数等因素综合评价。结果:(1)最小子野边长和最小子野面积对靶区剂量分布和计划执行效率影响较大,有统计学意义(P<0.05)。(2)强度分层等级和子野抑制因子对靶区剂量分布和计划执行效率影响较小,有统计学意义(P<0.05),前者取值超过10以后,评价指标除子野总数外,其余变化不明显,差异无统计学意义(P>0.05)。(3)SMT算法产生的子野总数约为SLD算法的90%,靶剂量分布更优,有统计学意义(P<0.05)。结论:(1)最小子野边长和最小子野面积为粗调,对剂量分布影响较大;强度分层等级和子野抑制因子为细调,对剂量分布影响较小,且达到某一特定值后趋于稳定。(2)SMT算法相比SLD算法生成的子野总数更少且剂量分布更优。
子野分割算法;SlidingWnd;SmartSequencing;剂量分布;计划执行效率
0 前言
调强放射治疗是通过建立目标函数进行逆运算生成各射野的通量强度分布,再根据各射野的通量强度分布利用子野分割算法产生若干调强子野序列,最终达到治疗靶区的剂量分布更加适形。其中,除了射野数目角度和目标函数及多叶准直器的各种物理限制以外,产生调强子野序列的各种子野分割算法也会对剂量分布产生影响,进而影响靶区和周围正常组织剂量。本研究利用鼻咽癌患者的调强计划,选取2种不同的调强子野分割算法SlidingWnd(简称SLD)和SmartSequencing(简称SMT),通过改变最小子野边长、最小子野面积、强度分层等级和子野抑制因子等取值,研究2种调强子野分割算法相关参数对剂量分布、机器跳数及子野总数等的影响。
1 材料与方法
1.1 病人资料
随机选取我院放疗中心2013年1月至6月收治的9例鼻咽癌患者,其中,男5例,女4例,中位年龄47岁,全部病例均经病理学证实为鳞状细胞癌。
1.2 CT定位及靶区和危及器官勾画
利用Orfit头颈部组件和热塑膜进行体位固定,西门子大孔径模拟CT螺旋扫描,上下界为眉弓上2cm至锁骨下5cm,层厚3mm,CT图像经MOSAIQ网络传输至XIO(版本:4.70)重建DRR,由医生在FOCAL工作站勾画靶区和危及器官。计划要求:95%靶体积PTV接受50Gy处方剂量,每周5次,2.0Gy/次。
1.3 计划设计
采用XIO治疗计划系统设计调强治疗计划,选取医科达Precise直线加速器(叶片在等中心投影为1cm),布野方案采用共面7野均分,机架角度分别为0°、52°、104°、156°、208°、260°、312°,射线质选用6MV X线,剂量算法选用Superposition算法,计算网格边长为2.5mm。根据靶区处方和危及器官受量设置计划约束条件,逆向优化生成各射野通量分布图,改变子野分割算法的有关参数产生不同的调强子野序列,取最小MU为5,实际计算剂量分布。SLD算法,最小子野边长(范围:0~3cm)取1cm、2cm、3cm产生L1、L2、L3共3组子野序列,强度分层等级(范围:2~20)取6、8、10、12、15产生SLD6、SLD8、SLD10、SLD12、SLD15共5组子野序列;SMT算法,最小子野面积(范围:0.1~100cm2)取2cm2、4cm2、6cm2产生A2、A4、A6共3组子野序列,子野抑制因子(范围:1~10)取3、5、7产生SMT3、SMT5、SMT7共3组子野序列。
1.4 评价指标
靶区评价指标有平均剂量(Dmean),剂量不均匀性指数(HI=D5%/D95%,其中D5%和D95%分别为5%和95%靶体积所受到的照射剂量,越接近1靶区剂量分布越均匀),靶区适形度指数(CI=(VT,ref/VT)×(VT,ref/Vref),其中,VT,ref为参考等剂量面所包绕的靶区体积,VT为靶体积,Vref为参考等剂量面所包绕的所有区域的体积。)串型危及器官的评价指标为最大点剂量(Dmax或D1%),并行危及器官的评价指标为受到特定剂量水平照射的体积百分比Vref。计划执行效率评价指标有机器跳数(MU)和子野数目(Number)。
1.5 统计学处理

2 结果
2.1 最小子野边长和最小子野面积对靶区剂量分布及计划执行效率的影响
(1)SLD算法,强度分层等级取8,最小子野边长分别取1cm、2cm和3cm,相关评价指标结果见表1。
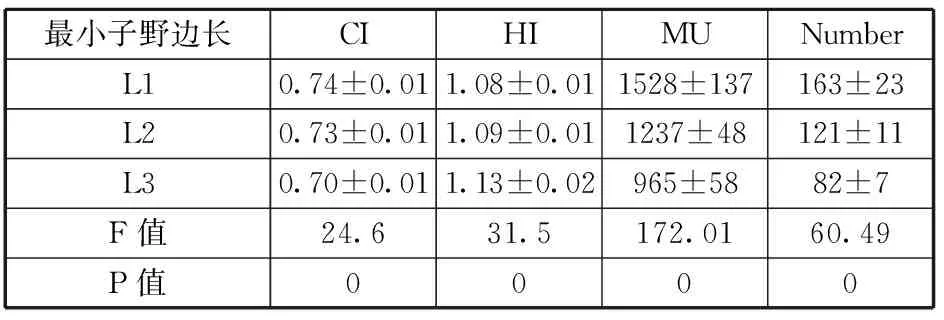
表1 最小子野边长对靶剂量分布和计划执行效率的影响
(2)SMT算法,子野抑制因子取5,最小子野面积分别取2cm2、4cm2和6cm2,相关评价指标结果见表2。
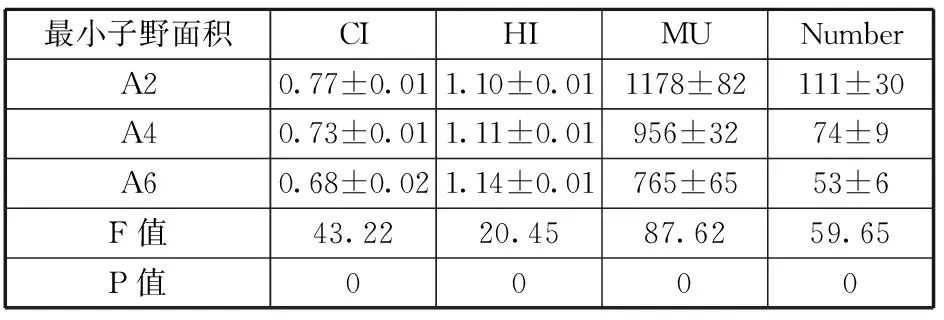
表2 最小子野面积对靶剂量分布和计划执行效率的影响
2.2 强度分层等级和子野抑制因子对靶区剂量分布及计划执行效率的影响
(1)SLD算法,最小子野边长取3cm,强度分层等级分别取6、8、10、12、15,相关评价指标结果见表3。

表3 强度分层等级对靶剂量分布和计划执行效率的影响
SLD10、SLD12、SLD15靶剂量分布和机器跳数差异不明显,差异无统计学意义(P=0.51)。
(2)SMT算法,最小子野面积取4cm2,子野抑制因子分别取1、3、5,相关评价指标结果见表4。

表4 子野抑制因子对靶剂量分布和计划执行效率的影响
2.3 MU统计学无差异情况下,SLD和SMT两种算法的子野总数和剂量学比较(见表5)。
SLD算法,最小子野边长取3cm,强度分层等级取8;SMT算法,最小子野面积取4cm2,子野抑制因子取5。两种算法,MU统计学差异不明显,P>0.05。
3 讨论
逆向调强放疗计划的制定过程与正向调强计划完全不同,计划设计者的主观干预在此期间至关重要。除合理设置靶区和危及器官剂量节制点、权重等目标函数外,还应灵活选择适宜的多叶准直器参数,以使设计的计划最优化。
最小子野边长和最小子野面积是两种子野序列算法中对剂量影响最大的因素,增加后会迅速减少子野数目和机器跳数,缩短患者治疗的时间和减少身体受照剂量,但与此同时,靶区剂量适形度和均匀性也下降,靶区外出现最大剂量点的概率增大,PTV外缘剂量下降的高梯度区消失。权衡靶剂量分布、治疗时间及计划执行精度等因素,建议最小子野边长为3cm,最小子野面积为4cm2。

表5 SLD算法和SMT算法对剂量分布和子野总数的影响
强度分层等级和子野抑制因子对剂量分布和计划执行效率的影响相对而言较小,有统计学意义,且达到某一固定数值以后,变化趋势相对平缓,如SLD方式,强度分层等级取10∽15,靶剂量分布、机器跳数变化均较小,仅表现为子野数目的小幅度增加。权衡靶剂量分布及计划执行效率等因素,建议强度分层等级取10,子野抑制因子取5。
SLD和SMT两种算法,在机器跳数无统计学差异的情况下,后者生成的子野总数更少,约等于SLD算法的90%,有统计学意义,靶区剂量分布方面,SMT算法的适形度和均匀性均优于SLD,差异有统计学意义,危及器官受量方面差异不明显,无统计学意义。分析原因可能为SMT算法生成的子野面积较大所致,某些情况下子野数目最少成为最好结果的标准,但在临床应用过程中,还必须考虑子野是否可以较好地实现,是否比较容易验证等问题。笔者在随后的调强计划面剂量验证中发现SLD算法生成的子野序列采用γ分析(3mm/3%)通过率绝大部分都高于SMT算法生成的子野序列,分析原因可能为SMT产生的子野形状比较复杂,排序较为混乱,MLC叶片形成相应形状所需运动的路径较长,叶片到位精度下降所致。
SLD和SMT算法都可以限制最小子野边长或面积,避免小MU数子野的出现,减少凹凸槽效应及离轴小野机头散射的不确定性,提高治疗剂量的准确度。
[1]Webb S.Optimization the planning of intensity-modulated radiotherapy[J].Phys Med Biol,1994,39:2229-2246.
[2]Bratengeier K.2-Step IMAT and 2-Step IMRT in three dimensions[J].Medical Physics,2005,32:3849-3861.
[3]Jin JY,FF Ryu S,et al.Dosimetric study using different leaf-width MLCs for treatment planning of dynamic conformal arcs and intensity-modulated radiosurgery.Med Phs,2005,32:405-411.
[4]余光伟,王连聪,等.多叶准直器参数对调强放疗计划的影响[J].中华放射肿瘤学杂志,2010,19:163-165.
[5]傅益谋,黄良,等.SmartSequence与SlidingWnd两种子野分割算法的比较[J].中国医学物理学杂志,2013,30:3851-3893.
[6]胡逸民.肿瘤放射物理学[M].北京原子能出版社,1999.Yimin Hu.Radiation oncology physics[M].Beijing Atomic Energy Press,1999.
The Effects of Segment Algorithm on Dose Distribution and Plan Execution Efficiency
LI Jin-kai,LI Cai-hong, WANG Pei-pei, SUN Xin-chen
(Department of Radiation Oncology,Nanjing medical university first affiliated hospital , Nanjing 210029)
Objective:To compare the effects of two segment algorithms of SlidingWnd and SmartSequencing used in Elekta XIO TPS (Version: 4.70) on the Dose Distribution and Plan Execution Efficiency. Methods: 9 patients with nasopharyngeal carcinoma were selected for the study. First of all,generated beam’s intensities for each patient by reverse optimization of IMRT plan; In the second, the different segments for each beam were created by changing the relative parameters of two segment algorithms. The SlidingWnd algorithm, 3 groups of segments were created by means of the Minimum-segment-size setted 1cm、2cm、3cm and 5 groups of segments by the Discrete-intensity-levels setted 6、8、10、12、15. The SmartSequencing algorithm, 3 groups of segments were created by means of the Minimum-segment-area setted 2cm2、4cm2、6cm2and the other 3 groups of segments by the Segment-suppression-factor setted 3、5、7. At last, compared the relative dosimetry differences which 14 groups of segments calculated to acquire, In addition, evaluate the factors of Machine Units and Segment number. Results: 1. The Minimum-segment-size and Minimum-segment-area has a great Effects on Dose Distribution and Plan Execution Efficiency,the differences were significant (P<0.05). 2. The Discrete-intensity-levels and Segment-suppression-factor has a little Effects on Dose Distribution and Plan Execution Efficiency, the differences were significant (P<0.05), the value of the former were setted more than 10, in addition to the segment number, the change of the rest evaluation index is not obvious, and the differences were not significant (P>0.05). 3. Compared with the SlidingWnd algorithm, the SmartSequencing algorithm could reduce the segment number by 10% and acquire better dose distribution, the differences were significant (P<0.05). Conclusions: 1. The factors of Minimum-segment-size and Minimum-segment-area have a great Effects on Dose Distribution and Plan Execution Efficiency, which is rough adjustment; The factors of Discrete-intensity-levels and Segment-suppression-factor have a little effects on Dose Distribution and Plan Execution Efficiency, which is fine adjustment and tends to be stable after reaching a certain value. 2. Compared with the SlidingWnd algorithm, the SmartSequencing algorithm could reduce the segment number and acquire better dose distribution.
segment algorithms; SlidingWnd; SmartSequencing; dose distribution; plan execution efficiency
2014-04-09
TH774
A
1002-2376(2014)08-0001-04
