Contour tracking using weighted structure tensor based variational level set
2014-08-08HUHongwei胡宏伟MABo马波CAOShujuan曹淑娟
HU Hong-wei(胡宏伟), MA Bo(马波), CAO Shu-juan(曹淑娟)
(Beijing Lab of Intelligent Information Technology, School of Computer Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
Contour tracking using weighted structure tensor based variational level set
HU Hong-wei(胡宏伟), MA Bo(马波), CAO Shu-juan(曹淑娟)
(Beijing Lab of Intelligent Information Technology, School of Computer Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
A novel contour tracking method using weighted structure tensor based variational level set is proposed in this paper. The image is first converted to weighted structure tensor field by extracting a positive definite symmetric covariance matrix for each pixel. Then, a level set method is employed to represent object contour implicitly which separates the image domain into two areas each modeled by tensor field based Gaussian mixture model separately. By solving a gradient flow equation of energy functional with respect to the level set, the object contour will converge to its real profile in the newly arrived frame. Experimental results on several video sequences demonstrate the better performance of our method than the other two contour tracking algorithms.
contour tracking; weighted structure tensor; Gaussian mixture model; level set
Contour tracking has been widely used in medical image processing, animation production, gesture recognition etc. The purpose of a contour tracker is to find the full profile of an object in one video frame utilizing the object model generated from the previous frame[1]. Many methods have been proposed in the field of contour tracking over the last few decades. Among these methods, the approach that evolves object contour by minimizing energy functional using optimization technology, such as gradient descent, has gained prominence in contour tracking field.
In fact, many contour tracking approaches are substantially based on segmentation. In order to model object contour, Kass et al.[2]proposed using active contour model, also called Snakes, to parameterize the curve of contour explicitly. Two terms are mainly utilized: one is called external energy functional and the other one is internal energy functional, aiming to evolve the curve by local minimization. It has become a classical method even though it suffers from several drawbacks, for example, heavily depending on its initial contour. The level set theory was first proposed by Osher et al.[3]based on Hamilton-Jacobi formulation which can perform numerical computation involving curves or surfaces on a fixed Cartesian grid without having to parameterize these objects. In Ref.[4], Cremers et al. showed a survey of a specific class of region-based level set segmentation methods and detailed statistical approaches for level set segmentation. By means of level set, it is easy to follow shape that splits or merges[5-6]in image segmentation and visual contour tracking. In order to solve the Eikonal equation with respect to level set faster, a fast marching level set method for monotonically advancing fronts was presented by Sethian[7]. Furthermore, fast adaptive narrow band level set was proposed in order to increase computing efficiency. During the procedure of minimizing energy functional, a signed distance function of level set is obliged, and, therefore, a costy re-initialization procedure is needed periodically. In order to remedy this problem, Li et al.[8-9]proposed a distance regularization term without the time-consuming re-initialization.
Due to a lot in common between segmentation and contour tracking, these approaches mentioned above utilized in segmentation could be applied in target contour tracking directly. Bertalmío et al.[10]presented tracking the deformation of the curves based on an additional, coupled PDE which performed by projecting the velocities of the first equation into the second one. Paragios et al.[11]proposed the model of geodesic active regions, and level set was used for motion estimation and tracking. However, this method is sensitive to illumination and ceases to be effective in the case of clutter. A real-time tracking algorithm for level set implementation proposed by Shi and Kark[12]was realized by simple operations of two linked lists without solving any partial differential equation. The methods based on tensor field are introduced in Refs.[13-14]. Rodrigo et al.[13]introduced an approach for tensor field segmentation based on the definition of mixtures of Gaussians on tensors as a statistical model. Zhan and Ma[14]presented a visual tracking method based on the tensor features. However, both the two approaches have not been used in contour tracking field.
In our approach, the well-known structure tensor[15]is adopted for object contour tracking to represent the feature of every pixel because of its abundant local information. Furthermore, two GMMs based on tensor feature[13]are used to model both inside and outside of the object region. The parameters, including Gaussian component weight, mean value and covariance of every single model, are obtained by expectation maximization (EM) algorithm using tensor samples extracted from target and background regions. A variational level set approach[16]is adopted to minimize the energy functional to achieve contour tracking. Experiments performed on several video sequences in which the objects suffer topology and illumination change, prove the effectiveness of the proposed approach.
Three main contributions of our paper are summarized as follows: ① we propose to use weighted structure tensor as the feature of a pixel which contains local information; ② the ensor field based Gaussian mixture model (TF-GMM) is the first introduced in the field of contour tracking to our knowledge; ③ a new energy functional is proposed in this paper which could achieve excellent experiment results.
The rest of this paper is structured as follows. Section 2 explains weighted structure tensor, tensors metric and the Gaussian mixture model for tensors. In section 3, the variational level set is discussed in detail and our approach to contour tracking on tensor image field is proposed. We perform our method on several challenging video sequences in section 4. Finally, in section 5, we summarize our work.
1 GMM on weighted structure tensor
1.1 Weighted structure tensor
Instead of using a scalar or vector feature, in this paper, we calculate a tensor feature[4-5]for each pixel in one image. At point (x,y), theN×Nstructure tensor is defined by
ST=f·fT,
(1)
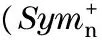
(2)


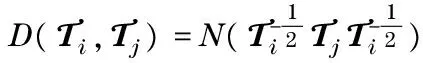
(3)
whereλidenotes the eigenvalues of tensorT.
(4)
whereωiis the weight of theith tensor. With the mean value of tensors, we can calculate covariance matrix for a tensor set by
(5)
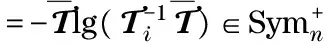
1.2 TF-GMM
Considering the definition of Gaussian distributions on scalars and vectors, we employ the tensor field based Gaussian mixture function (TF-GMM) used in Ref.[13] which is defined as


(6)

2 Variational level set method for tracking
2.1 Level set method
In Ref.[3], Osher and Sethian propose denoting moving fronts or active contoursCby a zero level setC(t)={(x,y)|φ(x,y,t)=0}implicitly. LetΩdenote image domain,Ω0the object region, and ∂Ω0the boundary set ofΩ0. The functionφis then defined as
(7)
wheredis the Euclidean distance from point (x,y) to the curve. The curve evolution under level set framework can be modeled by the following equation:
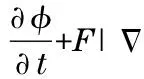
(8)

As far as curve evolution is concerned, level set methods can naturally address the topology change problem while this property doesn’t come easy for their parametric counterparts. An upwind scheme is often adopted as numerical implementation for hyperbolic conservation equation[6]to obtain a weak solution.
2.2 Tracking model
Inspired by Refs.[2,13,18] etc., we propose the following energy functional for object tracking
E(φ) =ηEi(φ)+μEl(φ)+νEs(φ),
(9)
whereη,μ,νare weights of the three functional components respectively, and every component will be detailed in the following.
Ei(φ) is an image energy functional which is defined as
Ei(φ)=ζEt(φ)+(1-ζ)Eb(φ),
(10)


whereEt(φ) is the target energy functional model, andEb(φ) is the background energy functional, andθ1is the GMM parameter vector obtained from target region of previous frame. Similarly,θ2is the GMM parameter vector for the background region. Besides,ζ∈[0,1] is used to balance target and background energy, andH(φ) is a Heaviside function. By minimizing the energy functional, one can drive the curve toward the object contour so that the internal region enclosed by the evolving contour conforms to the target GMM model, while its complement conforms to the background GMM model.
El(φ) is an edge modulated length term that encourages the evolution to get a more smoother curve and to stop at edge points. It is written as

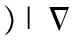
(11)
where edge functiong(x,y) is defined as
(12)
whereGσis a Gaussian smooth function,I(x,y) is the image intensity, andpis a constant (which is set to 2 in our experiments). As we can see,g(x,y) is positive in homogeneous regions, and reduces to zero at the edges. In Eq.(11),
(13)
isthedeltafunction.
Thelastterminourenergyfunctionalisshapeenergywhichdrivescurvesincurrentframeclosetotheshapeinpreviousone.Inourpaper,theshapepriormodelanditsupdaterefertoTaoZhang’swork[19]:

(14)
Giventheenergyfunctionalforvisualtracking,weneedtoderiveitscorrespondinggradientvectorflowtostartupthetrackingusinggradientdescentstrategy.Accordingtovariationalapproach,wehavethefollowinggradientflowequation:
∬ΩH(φ)lnPr(T(x,y)|θ1)dxdy)+
∬Ω(1-H(φ))lnPr(T(x,y)|θ2)dxdy))+
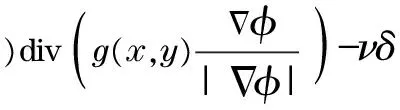
(15)
AR=∬ΩH(φ)dxdy,
ARC=∬Ω(1-H(φ))dxdy,
where div(·) is a divergence operator, and its numerical implementation requires delicacy.
3 Experiments
In the experiments, feature vectorfis defined as
f=(RGBIxIyIxxIyyIxy)T.
(16)
The size of local window is set to 7×7 when computing weighted structure tensor. For a gray-scale image, we just let gray-scale value replace the RGB values. In addition, the Heaviside function is replaced by a regularized function as follows
(17)
whereεis a control parameter. And as we can see

(18)
The delta function is rewritten as
(19)
Thevalueofεis set to 1 in our implementation in order to have a stable numerical calculation. We implemented our approach and performed it on several video sequences, and compared our method with other two state-of-art algorithms. One represents object region as a covariance matrix and tracks object contour under variational level set framework[20]. The other one proposed by Freedman et al.[21]tries to tracking object contour using distributions as object appearance representation. For the quantitative evaluation of our approach, an overlap ratio curve is shown in Fig.2. The overlap ratio is calculated as
(20)
whereAris the ground truth obtained manually, andAeis the internal area of evolution curve obtained by experiments. As we can see, the ratio is 1 when experimental contour overlap with real contour completely, and 0 when lose the tracking target.
In the first example, we tested our algorithm on a sequence named “walk front” with a pedestrian who was walking front. In this video, with the pedestrian walking out of the shade under trees, the illumination of the image was changed from dark to bright. What’s more, there were some other people walking with object of our interest which renders tracking difficult. The initial target contour was cropped by hand in the first frame, and the target could be tracked in the next several frames without changing any parameters. For the parameters, we setηto 150, the proportionζto 0.4,μto 2, and the weight of shape termνto 1 in our experiments. In Fig.1, we show the tracking results of three different experiments with their frame number are 1, 16, 50, 75, 102 and 140. Our approach can handle these problems successfully as is shown in Fig. 1a, and Fig. 2a for the quantitative comparison. The ratio of tracking results using our method is around 0.85 as is shown in Tab.1. Tracking results of the other two methods are also shown in Fig. 1a. From the comparison, we can clearly see that our method can produce better results.
The second video is “diving-lady” sequence. In this sequence, the target shape changes abruptly from time to time and as a result its statistical appearance model also changes very often. For the parameters, the weight of background energy is enlarged, andζis set to 0.1. Fig. 1b shows the comparison tracking results of this sequence with frame number 1, 5, 12, 22, 34 and 54, and Fig. 2b shows the overlap ratio curve. It is clear that our approach performs better in both the tracking results and the quantitative evaluation with the mean overlap ratio around 0.83 (see in Tab. 1). Furthermore, our method is more robust comparing with the other two state-of-art methods (see the overlap ratio shown in Fig. 2b).

Fig.1 Comparison of tracking results

Fig.2 Overlap ratio curves
We also applied our algorithm on a face sequence named “seq_mb_clip”. The face region of a woman who moved around in this sequence was tracked. An obstacle arising obviously from this video is that the color in part of background is similar to that of target region, and the scale of target contour changes with time. The top row in Fig. 1c shows the tracking results of our method and the other two different experiments with frame numbers 1, 6, 15, 25, 43 and 61. Although the tracking results of covariance matching are comparable between our method and other methods, we get a larger mean value which is 0.869 2 and smaller variance as is shown in Tab.1. Fig.2c shows the overlap ratio of our method with the other two state-of-art approaches. The visual and quantitative comparisons demonstrate the robustness and accuracy of our method.

Tab.1 Mean and variance of overlap ratio
Fig.3 presents some other tracking results using our method. From all these tracking results, we demonstate that our approach can handle geometric distortion (“diving-lady”), clutter (“fish”) , illumination changes (“walk front”), scale changes (“seq_mb_clip”, “fish”) and partial occlusion (“car”) fairly well.

Fig.3 Tracking results of others
4 Conclusion
In this paper, a variational level set method has been proposed for contour tracking. The vector image data are first transformed into weighted tensor field. It ensures that the tensor field is modeled by GMMs. Alongside the edge modulated length item and shape prior item, the image item based on GMMs for tensor data is adopted for contour tracking. The experimental results prove the validity of the proposed method.
[1] Yilmaz A, Javed O, Shah M. Object tracking: a survey[J]. ACM Computing Surveys (CSUR), 2006, 38(4): 13.
[2] Kass M, Witkin A, Terzopoulos D. Snakes: active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331.
[3] Osher S, Sethian J A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49.
[4] Cremers D, Rousson M, Deriche R. A review of statistical approaches to level set segmentation: integrating color, texture, motion and shape[J]. International Journal of Computer Vision, 2007, 72(2): 195-215.
[5] Sethian J A. Level set methods and fast marching methods: evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science[M]. Cambridge:Cambridge University Press, 1999.
[6] Sethian J A. Adaptive fast marching and level set methods for propagating interfaces[J]. Acta Math Univ Comenianae, 1998, 67(1): 3-15.
[7] Sethian J A. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences, 1996, 93(4): 1591-1595.
[8] Li C, Xu C, Gui C, et al. Level set evolution without re-initialization: a new variational formulation[C]//Computer Vision and Pattern Recognition, 2005. CVPR 2005. Computer Society Conference on IEEE, 2005, 1: 430-436.
[9] Li C, Xu C, Gui C, et al. Distance regularized level set evolution and its application to image segmentation[J]. Image Processing, IEEE Transactions on, 2010, 19(12): 3243-3254.
[10] Bertalmio M, Sapiro G, Randall G. Morphing active contours[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2000, 22(7): 733-737.
[11] Paragios N, Deriche R. Geodesic active regions and level set methods for motion estimation and tracking[J]. Computer Vision and Image Understanding, 2005, 97(3): 259-282.
[12] Shi Y, Karl W C. Real-time tracking using level sets[C]//Computer Vision and Pattern Recognition, 2005. CVPR 2005. Computer Society Conference on IEEE, 2005, 2: 34-41.
[13] de Luis-García R, Westin C F, Alberola-López C. Gaussian mixtures on tensor fields for segmentation: applications to medical imaging[J]. Computerized Medical Imaging and Graphics, 2011, 35(1): 16-30.
[14] Zhan X, Ma B. Gaussian mixture model on tensor field for visual tracking[J]. Signal Processing Letters, IEEE, 2012, 19(11): 733-736.
[15] Donoser M, Kluckner S, Bischof H. Object tracking by structure tensor analysis[C]//Pattern Recognition (ICPR), 2010 20th International Conference on IEEE, 2010: 2600-2603.
[16] Zhao H K, Chan T, Merriman B, et al. A variational level set approach to multiphase motion[J]. Journal of Computational Physics, 1996, 127(1): 179-195.
[17] Pennec X, Fillard P, Ayache N. A Riemannian framework for tensor computing[J]. International Journal of Computer Vision, 2006, 66(1): 41-66.
[18] Chan T F, Vese L A. Active contours without edges[J]. Image Processing, IEEE transactions on, 2001, 10(2): 266-277.
[19] Zhang T, Freedman D. Tracking objects using density matching and shape priors[C]//Computer Vision, 2003. Proceedings Ninth IEEE International Conference on IEEE, 2003: 1056-1062.
[20] Ma B, Wu Y. Covariance matching for pde-based contour tracking[C]//Image and Graphics (ICIG), 2011 Sixth International Conference on IEEE, 2011: 720-725.
[21] Freedman D, Zhang T. Active contours for tracking distributions[J]. Image Processing, IEEE Transactions on, 2004, 13(4): 518-526.
(Edited by Wang Yuxia)
2013- 02- 29
Supported by the National High-Tech Research & Development Program of China (2009AA01Z323)
TP391.41 Document code: A Article ID: 1004- 0579(2014)02- 0218- 08
E-mail: bma000@bit.edu.cn
杂志排行
Journal of Beijing Institute of Technology的其它文章
- Expert ranking method based on ListNet with multiple features
- Investigating fatigue behavior of gear components with the acoustic emission technique
- Consensus problem of multi-agent systems under arbitrary topology
- One-piece coal mine mobile refuge chamber with safety structure and less sealing risk based on FEA
- Three-dimension micro magnetic detector based on GMI effect
- On measured-error pretreatment of bionic polarization navigation
