Consensus problem of multi-agent systems under arbitrary topology
2014-08-08DONGLijing董立静CHAISenchun柴森春ZHANGBaihai张百海
DONG Li-jing(董立静), CHAI Sen-chun(柴森春), ZHANG Bai-hai(张百海)
(School of Automation, Beijing Institute of Technology, Beijing 100081, China)
Consensus problem of multi-agent systems under arbitrary topology
DONG Li-jing(董立静), CHAI Sen-chun(柴森春), ZHANG Bai-hai(张百海)
(School of Automation, Beijing Institute of Technology, Beijing 100081, China)
Consensus problem of second-order leader-following multi-agent systems under arbitrary topology is investigated in this paper. Arbitrary topology means the variable topology shifts continuously rather than switches among several different structures. For ensuring the consensus of leader-following multi-agent systems, some sufficient conditions and controller design principles are deduced both for a double-integrator case and a nonlinear case. Certainly, numerical simulations are carried out to prove the feasibility and effectiveness of theory derivation, which vividly illustrates that the following agents can successfully track the leader agent.
nonlinear multi-agent system; consensus; arbitrary topology
Since consensus of multi-agent systems (MAS) is a fundamental problem in the MAS research area, it has attracted increasing attention of researchers from various disciplines of engineering, biology and science. In multi-agent systems, consensus means to reach an agreement regarding a certain quantity of interest that depends on the states of all agents. A consensus algorithm is an interaction rule that specifies the information exchange between an agent and all of its neighbors in the network. Such problems have been formulated as consensus of leaderless problems or leader-following problems[1-3]. For a cooperative multi-agent system, leaderless consensus means that each agent updates its state based on local information of its neighbors such that all agents eventually reach an agreement on a common value, while leader-following consensus means that there exists a virtual leader which specifies an objective for all agents to follow.
In the past few years, the multi-agent systems with integer dynamics[4-6]or invariant topology[1,4-5]have been widely studied by many researchers due to its simple construction and convenience to analyze. Certainly, there are some researchers spending effort on multi-agent system with nonlinear dynamics[1, 7]or switching topologies[2, 6, 8], and there have been some outcomes. In Ref.[1] a pinning control algorithm was proposed to achieve leader-following consensus in a network of agents with nonlinear second-order dynamics. Ref.[7] proposed an adaptive distributed controller with a disturbance estimator to solve the consensus problem under a fixed topology. By using a common Lyapunov function, Ref.[2] extended leader-following consensus control for multi-agent systems, which ensured strong mean square consensus, to the switching topology case. In Ref.[6], the sampled control protocols were induced from continuous-time linear consensus protocol by using periodic sampling technology and zero-order hold circuit. Nevertheless, since consensus problem of multi-agent systems associated with both nonlinear dynamics and variable topology, it is extremely difficult and complicated, people hardly discuss about it.
However, considering the fact that almost all the physical plants contain nonlinearity and the communication topology may change from time to time, therefore, the velocity of each agent is time-varying and the communication radius is finite, consensus problem of multi-agent systems with nonlinear dynamics and variable topology is of vital necessity. However only a few researchers have paid attention on the consensus problem of multi-agent systems under arbitrary topology. In Ref.[9], H. Kim addresses the problem of consensus of multi-agent systems, consisting of a set of identical MIMO LTI systems, under a time-varying network that has a well-defined average (with uniform convergence to the average). A. Popov[10]proposed a sufficient scaled l1 stability condition for arbitrary topology. By employing some knowledge of complex dynamical network, the author has discussed the consensus problem of first-order leader-following multi-agent system under arbitrary topology in Ref.[11]. This paper will discuss the second-order multi-agent consensus problem under arbitrary topology situation. Based on the author’s work in Ref.[11], some sufficient conditions and controller design principles are given to ensure consensus of the second-order nonlinear multi-agent system under arbitrary topology.
The paper is organized as follows. Some preliminaries of graph theory are briefly reviewed in section 1. Main results are presented in section 2. To illustrate the proposed theoretical results, numerical simulations are provided in section 3. And finally, conclusions are drawn in section 4.
1 Problem description and preliminaries
In this section, we describe the second-order multi-agent system model on which the consensus problemwas brought about. In addition, a brief summary of the relevant results in graph theory and control stability, by merging which we are able to analyze the consensus, is provided. Finally, the relevant notations are presented.
1.1 Problem description
The system to be considered in this paper is a leader-following multi-agent system. The second-order multi-agent system is composed of one virtual leader agent andNnonlinear coupled following agents, labeled from 1 toN. The virtual leader agent is described with the following dynamic:
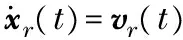
(1a)
wherexr∈Rmandvr∈Rmare position and velocity states of the virtual leader respectively.f(t,xr,vr)∈misanonlinearcontinuousfunctiontodescribetheself-dynamicsoftheleaderagent.Thisisanactiveleaderwhenf(t,xr,vr)≠0, which means the velocity of leader is time-varying.Whenf(t,xr,vr)=0, the leader posses a constant velocity.
The following agents are assumed to have the second-order dynamics as
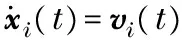
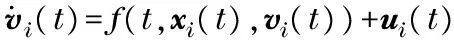
i∈{1,2,…,N},
(1b)
wherexi∈Rmandvi∈Rmare position and velocity states of agentirespectively,f(t,xi,vi)∈Rmis a nonlinear continuous function to describe the self-dynamics of agenti,ui∈Rmare control input of agenti. Whenf(t,xi,vi)=0, the dynamics of multi-agent system will turn into double-integrator dynamics with a constant reference velocity.
The objective of this paper is to design a control protocol which ensures the following agents effectively pursue the leader agent under arbitrary topology.
1.2 Preliminaries
To analyze the consensus problem of second-order leader-following multi-agent systems, some relevant theories in graph theory and control stability are recalled.
A weighted graph denoted byG={v,ε,A} with a node setv={1,2,…,N},an edge setε⊆v×vand a weighted adjacency matrixA=(aij)N×Nwith nonnegative elements[12]. We consider that (i,j)∈εif and only if vertex (node)ican send its information to vertexj. If (i,i)∈ε, we say that vertexihas the self-loop. In this paper, it is assumed that no self-loop exists. The set of neighbors of vertexiis denoted byNi={j|j∈v,(j,i)∈ε}, whenj∉Ni, which means there is no information flow from vertexjto vertexi, thenaij=0, otherwiseaij>0. The in-degree and out-degree of nodeiare, respectively, defined as[13]
DenoteDdiag{degin(1),degin(2),…,degin(N)},thentheLaplacianmatrixLofthegraphGisdefinedasLD-A.
Fromthegraphtheorypointofview,everyagentcanbetreatedasavertex.Thenthemulti-agentsystemcanbetreatedasadynamicgraphGwhenitisanalyzedintheory.
Inthispaper, aij,theweightedvalueofagentjtoagenti,isconscioustime-varying,anditisdenotedasaij(t),whichmeansthetopologyofmulti-agentsystemisarbitraryalongwithtime.
Definition 1 The leader-following multi-agent system (1) is said to achieve second-order consensus when following equation is satisfied.
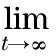
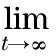
(2)
Lemma 1[14]Let Abearealsymmetricn×n-matrixandλmax(A)≥λi(A)≥λmin(A)(i=1,2,…,n), then the following inequality equation on inner product is established.
λmax(A)〈X,X〉≥〈AX,X〉≥λmin(A)〈X,X〉.
1.3 Notations
Some mathematical notations are used throughout this paper. DenoteIN∈RN×Nas anN-dimensional identity matrix, 1N=[1,1,…,1]T∈RNas a vector of all ones. LetATandA-1be the transpose and the inverse of matrix Arespectively.λmax(A) denotes the maximal eigenvalue of matrixAandλmin(A) denotes the minimal eigenvalue of matrixA. ‖·‖ denotes Euclidean norm.
2 Main results
This section presents control protocol design principle and the consensus proof of second-order leader-following multi- agent systems under arbitrary topology under two cases:
Case Ⅰ:f=0 (double integrator dynamics)
Case Ⅱ:f≠0 (nonlinear dynamics)
In the two cases, the control protocol is adopted in the following format for each agent:
(3)
whereγ>0 andk>0 are parameters to be designed.bi(t) indicates the accessibility of the leader agent by the following agentiat timet.bi(t)>0 indicates the case that agentican get the position and velocity value of the leader at timet, andbi(t)=0 indicates the case that the information of leader agent is not accessible by the following agenti.
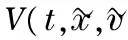
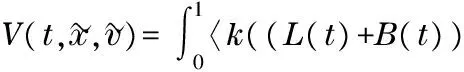
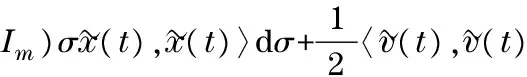
(4)
2.1 Consensus with double integrator dynamics
In case off=0, the second-order multi-agent system is reduced into the following double-integrator system (5) with control protocol (3).
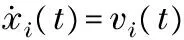
(5)
Andtheleaderagentisdescribedby

(6)
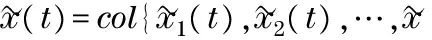
Combining the following agents (5) and the leader agent (6), disagreement equation can be deduced as


(7)
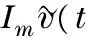
In this case, the following result about consensus problem of multi-agent system under arbitrary topology is established.
Theorem 1 The second-order leader-following consensus of multi-agent system (5) under arbitrary topology is achieved if the following conditions are satisfied.
(i)λmin((L(t)+B(t))⊗Im)>0
(ii) The derivation d((L(t)+B(t))⊗Im)/dtexists andλmax(d((L(t)+B(t))⊗Im)/dt)<0.
ProofIntheviewofLemma1,itisclearthat
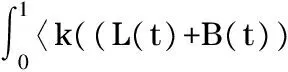
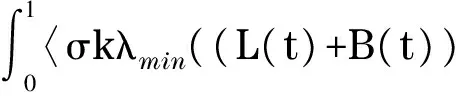
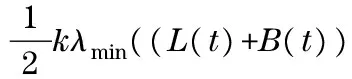
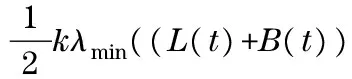
(8)
By employing the Lyapunov function (4) and the above inequality (8), it follows that
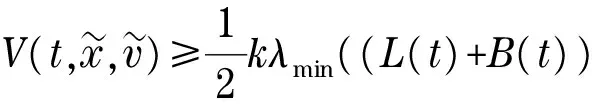
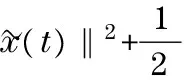
(9)
Fork>0 andλmin((L(t)+B(t))⊗Im)>0, it is clear that the Lyapunov function defined in Eq.(4) is positive definite in this case.
The derivation of Lyapunov function (4) along the disagreement system (7) is deduced as
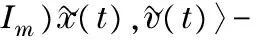


(10)
Itisclearthat

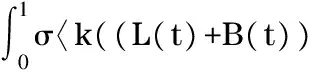
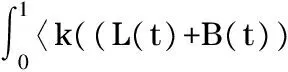
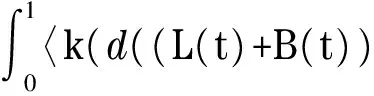
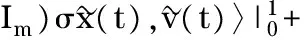
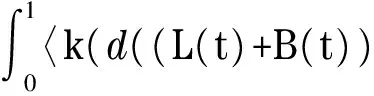
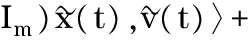
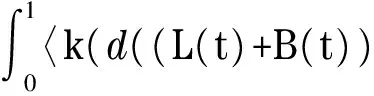
(11)
Substitute Eq.(11) into Lyapunov function’s derivation (10), consequently, Eq.(10) can obtained as

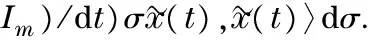
(12)
InviewofLemma1,itisclearthat
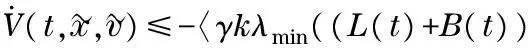
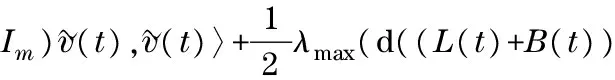

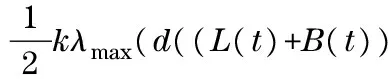
(13)
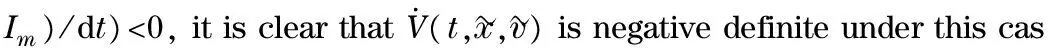
Accordingtotheaboveillustrations,wecanconcludethatconditions(i)and(ii)inTheorem1ensurethestabilityofthedisagreementsystem(7).FromDefinition1,thecontrolprotocol(3)solvestheconsensusproblemofsecond-ordermulti-agentsystem,inwhichthefollowingagents’dynamicmodelisEq.(5)andtheleaderagent’sdynamicmodelisEq.(6),underarbitrarytopologywithoutanyspecialrequestforcontrolparameterγandk. This completes the proof.
2.2 Consensus with second-order nonlinear dynamics
In the case off≠0, the second-order following agents’ dynamics Eq.(1b) become system (14) with control protocol (3). The leader, in this case, is an active agent described by Eq.(1a).
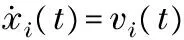
(14)
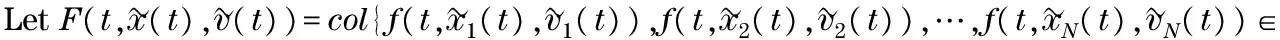
Assumption 1 For the nonlinear functionf, there exists a constantl>0 such that ‖f(t,xi(t),vi(t))-f(t,xr(t),vr(t))‖≤l(‖xi(t)-xr(t)‖+‖vi(t)-vr(t)‖) which indicates
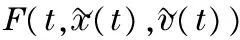
(15)
Combining system (14) and the virtual leader (1a), the disagreement multi-agent system can be deduced.
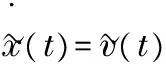

B(t))⊗⊗).
(16)
In this case, the following consensus theorem of second-order leader-following system with nonlinear self-dynamic is established.
Theorem 2 The second-order leader-following consensus of multi-agent system (14) is achieved if all the conditions in Theorem 1 hold and the control parametersγ,ksatisfy the following conditions.
(i)k>-l/λmax(d(L(t)+B(t))⊗Im/dt)
(ii)γk>3l/2λmin((L(t)+B(t))⊗Im).
Proof Under the conditions in Theorem 2 and consider the proof of Theorem 1, it can be easily seen that
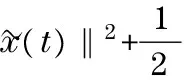
(17)
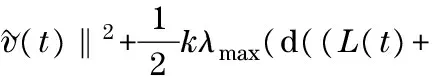
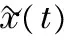
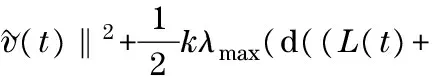
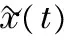


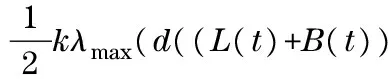
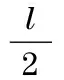
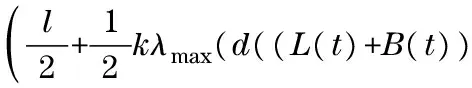


(18)
3 Numericalexamples
Inthissection,asecond-ordermulti-agentsystemwhichconsistsof1leaderagentand3followingagentsisemployedtoverifythefeasibilityandeffectivenessofthiswork.TwoapplicationsofTheorem1andTheorem2arecarriedout.Theleaderandfollowingagentsaredescribedas
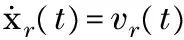
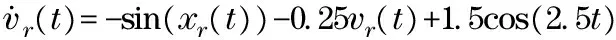
(19)
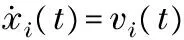
1.5cos(2.5t)+ui(t),i∈{1,2,3},
(20)
wherex∈R3andv∈R3are position and velocity states of the agents in 3-dimensional respectively. The nonlinear continuous functionf(t,x,v) is embodied by
-sin(x(t))-0.25v(t)+1.5cos(2.5t).
As the topology of multi-agent system is arbitrary, Laplacian matrix of topology graph at timetis described by a time-varying matrix (L(t)+B(t))⊗I3.AndL(t)+B(t)isembodiedas
(21)
wherea11=(e2-1)th(t)+earctan(t),a12=(1-e)th(t)-2earctan(t),a13=earctan(t),a22=th(t)-2e2arctan(t),a23=2th(t)+e2arctan(t),a33=3(e-e2)th(t)+arctan(t).
The leader’s initial position and velocity in 3-dimensional are
xr(0)=[0 0 0],
vr(0)=[0.03 0.02 -0.04].
The position and velocity in 3-dimensional of the 3 following agents are initialized as
x1(0)=[0.05 -0.04 0.01],
x2(0)=[-0.05 0.03 -0.07],
x3(0)=[0.03 -0.06 0.08],
v1(0)=[0.05 -0.01 0.01],
v2(0)=[-0.04 0.05 0.03],
v3(0)=[-0.05 0.08 -0.01].
3.1 Multi-agent system with double-integrator dynamics
In this case, the nonlinear function in Eqs.(19) (20) is replaced by 0. Arbitrary topology and the above mentioned initial conditions are employed in this simulation. Fig.1 and Fig.2 present the position and velocity disagreement vectors of the leader and 3 following agents with double-integrator dynamics.
-sin(x(t))-0.25v(t)+1.5cos(2.5t)

Fig.1 Position errors of the multi-agent system with double-integrator dynamics
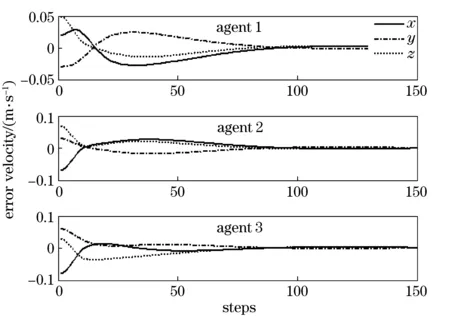
Fig.2 Velocity errors of the multi-agent system with double-integrator dynamics
From Fig.1 and Fig.2, it is obvious that the following agents can track the leader effectively in 150 steps under arbitrary topology. This is a good explanation of the theoretical derivation in section 2.1.
3.2 Multi-agent system with nonlinear dynamics
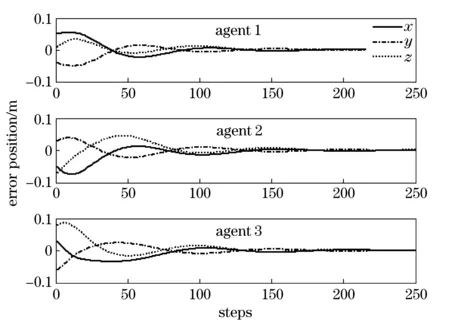
Fig.3 Position errors of the multi-agent system with nonlinear dynamics
In this case, the multi-agent system is described exactly the same as Eqs.(19) (20) under the arbitrary topology and the above mentioned initial conditions. Fig.3 and Fig.4 present the position and velocity disagreement vectors of 3 following agents relative to the leader with nonlinear dynamics.
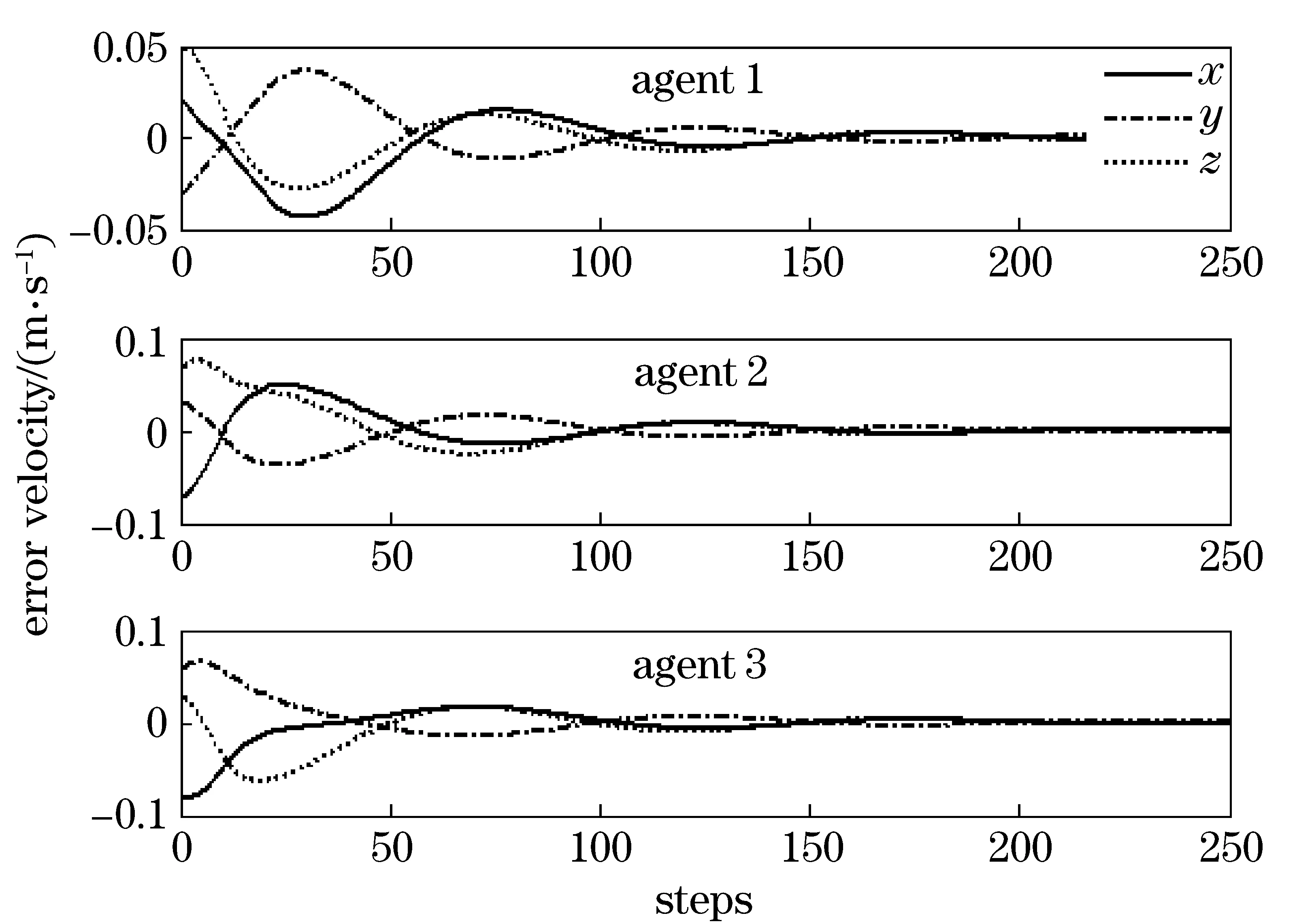
Fig.4 Velocity errors of the multi-agent system with nonlinear dynamics
From Fig.3 and Fig.4, we can see that the position disagreement and velocity disagreement of the following agents with leader converge to zero in 250 steps, which indicates that the following agents can track the active leader in finite time nicely. This is a good explanation to theoretical derivation in section 2.2.
By comparing the results in section 3.1 and section 3.2, the disagreement vectors of the multi-agent system with double-integrator dynamics converge faster than that with nonlinear dynamics.
4 Conclusion
This paper discusses the consensus problem of second-order multi-agent systems under arbitrary topology. Some sufficient conditions are obtained with the proposed control protocol and numerical simulations are employed to verify them. The multi-agent systems can reach consensus in both double-integrator case and nonlinear case. The response time of multi-agent system with double integrator dynamics is shorter. It is obvious that nonlinearity impedes the convergence rate, which tantalizingly hints that it is needed to design a more advanced controller in the future work.
[1] Song Q, Cao J D, Yu W W. Second-order leader-following consensus of nonlinear multi-agent systems via pinning control[J]. Systems & Control Letters,2010, 59: 553-562.
[2] Ni W, Cheng D. Leader-following consensus of multi-agent systems under fixed and switching topologies[J]. Systems & Control Letters, 2010,59(3C4): 209C217.
[3] Ren W. Consensus tracking under directed interaction topologies: algorithms and experiments[J]. IEEE Trans Control Syst Technology, 2010,18(1) :230 -237.
[4] Li S H, Dua H B, Lin X Z. Finite-time consensus algorithm for multiagent systems with double-integrator Dynamics[J]. Automatica,2011, 47:1706-1712.
[5] Hua J P, Feng G. Distributed tracking control of leader-follower multiagent systems under noisy measurement[J]. Automatica,2010, 46: 1382-1387.
[6] Xie G M, Liu H Y, Wang L, et al. Consensus in networked multi-agent systems via sampled control: switching topology case[C]∥2009 American Control Conference, 2009:4525-4530.
[7] Sumizaki K, Liu L, Hara S. Adaptive consensus on a class of nonlinear multi-agent dynamical systems[C]∥SICE Annual Conference 2010 August 18-21,2010: 1141-1145.
[8] Münz U, Papachristodoulou A, Allgöwer F. Consensus in multi-agent systems with coupling delays and switching topology[J]. IEEE Trans Automat Control,2011,56(12):2976-2982.
[9] Kim H, Shim H, Back J, et al. Consensus of output-coupled linear multi-agent systems under fast switching network: averaging approach[J].Automatica, 2013, 49: 267-272.
[10] Popov A, Werner H. Robust stability of a multi-agent system under arbitrary and time-varying communication topologies and communication delays[J]. IEEE Trans Automat Control, 2012,57(9): 2343-2347.
[11] Dong L J, Chai S C, Zhang B H. Necessary and sufficient conditions for consensus of multi-agent systems with nonlinear dynamics and variable topology[C]∥2012 UKACC International Conference on Control, 2012:1052-1056.
[12] Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Trans Automat Control,2004, 49 (9) : 1520-1533.
[13] Song Q, Cao J. On pinning synchronization of directed and undirected complex dynamical networks[J]. IEEE Trans Circuits Syst,2010, I57 (3) : 672-680.
[14] Mirsky L. An introduction to linear algebra[M]. New York: Dover Publications, Inc.,1990.
(Edited by Wang Yuxia)
2013- 03- 01
Supported by Scientific Research and Postgraduate Training Joint-Build Project (20120639002); the National Natural Science Foundation of Youth Science Fund (61104086)
TP 202.1 Document code: A Article ID: 1004- 0579(2014)02- 0210- 08
E-mail: chaisc97@bit.edu.cn
杂志排行
Journal of Beijing Institute of Technology的其它文章
- Expert ranking method based on ListNet with multiple features
- Investigating fatigue behavior of gear components with the acoustic emission technique
- Contour tracking using weighted structure tensor based variational level set
- One-piece coal mine mobile refuge chamber with safety structure and less sealing risk based on FEA
- Three-dimension micro magnetic detector based on GMI effect
- On measured-error pretreatment of bionic polarization navigation
