几乎Prüfer整环的反向极限

周 霞

(西南财经大学天府学院，四川绵阳621000)

D.E.Dobbs等［1］讨论了局部的 Prüfer整环(即赋值整环)的反向极限是局部的Prüfer整环，在非局部的情形下，只有在riding假设的条件下，才有Prüfer整环的反向极限是 Prüfer整环.鉴于此，本文主要讨论了几乎 Prüfer整环(即设a，b∈R-{0}，存在某个正整数n，使得(an，bn)是可逆理想［2-5］)的反向极限.证明了几乎赋值整环的反向极限是几乎赋值整环(即设a，b∈R-{0}，存在某个正整数n，使得an|bn或bn|an［2-5］)，几乎 Prüfer整环在 riding假设的条件下仍是几乎Prüfer整环.给出了例子说明几乎 Prüfer整环的反向极限未必是几乎Prüfer整环，并在第2部分的基础上减弱riding假设的条件，得到了若(An，φn，m)是反向系统，设是(An，φn，m) 的相伴反向系统，An是几乎Prüfer整环，则A*是几乎 Prüfer整环.对 D.E.Dobbs等在文献［1］的注记2.4(b)的问题给出了一个答案.为了本文讨论的需要，将一些相关内容陈述如下.

设(I，≤)是正向偏序集(并不是必须规定I是正向的)，设{An:n∈I}是一簇环，且有一簇同态{φn，m:An→Am，其中n≥m}满足:

1) φn，n是An的恒等映射；

2) φm，l= φm，n◦φn，l，其中l≤n≤m，

则称(An，φn，m)是I上的环和态射的反向系统.

定义反向系统(An，φn，m)的反向极限

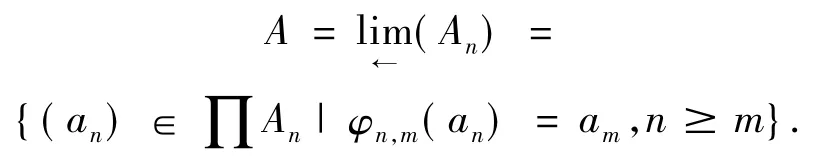
显然，A是An的子环.对反向极限A，有标准映射Φn:A→An.于是在同构意义下，反向系统的反向极限存在时是唯一的.

本文所研究的是在正整数指标集N下的反向极限，所讨论的整环都是有单位元的交换整环.恒用qf(A)表示环A的商域.

1 反向极限的预备知识

为了后面叙述的方便起见，首先给出强Milnor方图的定义.设如图1所示的拉回图满足T是整环，M是T的非零的极大理想，R是T的真子环，F=T/M是域，于是M是R的素理想，D=R/M是F的真子环，φ是自然同态，则图1称为强Milnor方图(有关强Milnor方图的更多性质与作用请参见文献［6-8］).

图1

引理 1.1设(An，φn，m:An→Am；n≥m≥1)是交换环的反向系统，φn，n是恒等映射，且设是反向极限.令Φn:A→An是标准映射，Qn=Ker(Φn)，则:

1)A={(an) ∈ ∏An|φn+1，n(an+1)=an，对每个n∈N}；

2)对每个n∈N，Φn是包含映射A→∏Ak与标准投射∏Ak→An的合成；

3) 对每个n∈N，Qn={(ak)∈A|ak=0，对每个k≤n}；

4)Q1⊇Q2⊇Q3⊇…，且∩Qn=0；

5)如果对每个n∈N，An是整环，则A是整环；

6)如果对每个n∈N，An是赋值整环，则A是赋值整环.

下面给出riding假设及其记号.设对每个n，{A1；(Fn，Bn):n∈N}满足:

1)Bn是局部整环，且有极大理想Mn≠0；

2)Fn=Bn/Mn，φn:Bn→Fn是满射且

3)A1是整环但不是域，qf(A1)⊆F1.

对每个n，设An+1是Bn×FnAn的如图2所示的拉回图.

图2

则An+1包含于Bn，从而包含于Fn+1.因为Mn≠0，An+1和Bn有公共的非零理想，且

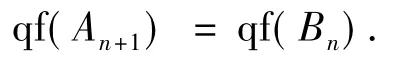
显然，图2是强Milnor方图.因此，由上述条件可得如图3所示的拉回图集.

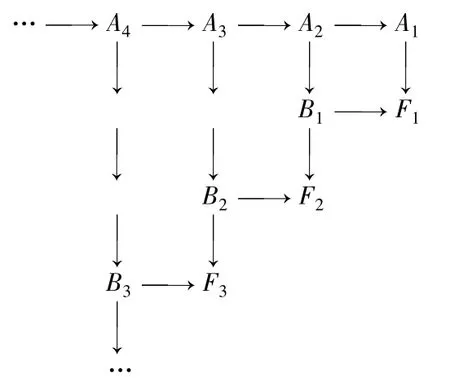
图3

其中 φn，n-1:An→An-1是满射，因为对.如果n≥m，考虑下述满射

且 φn，n:An→An取恒等映射.由同态 φn，m所决定的反向系统称为是由{A1；(Fn，Bn):n∈N}所生成的反向系统.令

Φn:A→An是标准映射，且Qn=Ker(Φn).

引理1.2在riding假设下，有:

1)对每个n∈N，Φn是满射；

2) 对每个n∈N，Qn∈Spec(A)且A/Qn≅An，因此A是整环；

3) 对每个n∈N，Mn=Ker(φn+1，n)且

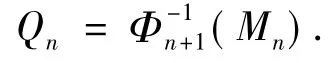
在文献［9］中，设R是整环，对P∈Spec(R)，称P是R的除子素理想，如果PRP=P；或者等价于如图4所示的同态图形.

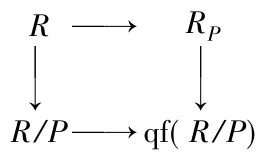
图4

显然图4是一个强Milnor方图.

2 几乎Prüfer整环在riding假设下的反向极限

因为几乎赋值整环在对几乎Prüfer整环的刻画中起着重要作用，所以在本部分中首先考虑几乎赋值整环的反向极限问题.

定理 2.1设(An，φn，m:An→Am；n≥m≥1)是交换环的反向系统，φn，n是恒等映射，且A=lim←(An)是反向极限.令 Φn:A→An是标准映射，Qn=Ker(Φn).如果对每个n∈N，An是几乎赋值整环，则A也是几乎赋值整环.

证明任取 α=(αn)，β=(βn)∈A，只需证明存在某个正整数 γ，使得 αγ∈Aβγ或 βγ∈Aαγ即可.

情形1因为An是几乎赋值整环，从而对每个n∈N，取 μn∈An，存在某个正整数 γ，使得

又因为A是整环，则或者或者

若，则 φn，m(μn)= μm，从而 μ =(μn)∈A，显然有αγ=μβγ.若对某个m∈N，βm=0m，不妨设k是使得βm=0m的最大的正整数(即对m＞k，有βm≠0m；m≤k，有 βm=0m)，从而对n≥m＞k，φn，m(μn)=μm，而对 1≤i≤k，

因为存在反向系统，故对n≥m，φn，m(vn)=vm，于是v∈A.那么，对每个n，有，所以

情形2设对某个n＞m，因为An、Am都是几乎赋值整环，从而取rn∈An，sm∈Am，存在某个正整数γ，使得

由上述定理知，几乎赋值整环的反向极限是几乎赋值整环，接下来讨论几乎Prüfer整环在riding假设条件下的反向极限.

推论2.2下述条件等价:

1)对每个n∈N，An是几乎赋值整环；

2)A1是几乎赋值整环，且对每个n∈N，Bn是几乎赋值整环，qf(An)⊆Fn是根扩张；

3)A是几乎赋值整环.

证明1)⇒3) 由定理2.1可知.

3)⇒1) 因为A是几乎赋值整环且

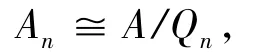
故An是几乎赋值整环.

1)⇔2) 考虑如图5所示的强Milnor方图.

图5

由文献［10］的定理2.2知，An+1是几乎赋值整环当且仅当An和Bn均是几乎赋值整环，且qf(An)⊆Fn是根扩张.重复该结果，可得1)⇒2)和2)⇒1).

定理2.3下述条件等价:

1) 对每个n∈N，An是几乎Prüfer整环；

2)A1是几乎 Prüfer整环，且对每个n∈N，Bn是几乎赋值整环，qf(An)⊆Fn是根扩张；

3)A是几乎Prüfer整环.

证明3)⇒1) 因为A是几乎 Prüfer整环且An≅A/Qn，故An是几乎 Prüfer整环.

1)⇒3) 对每个P∈Spec(A)，由文献［1］的命题2.15知，对所有n≥m=m(P)有

又因为An是几乎Prüfer整环，故(An)Pn是几乎赋值整环，由定理2.1知，AP是几乎赋值整环，所以A是几乎 Prüfer整环.

1)⇔2) 考虑如图5所示的强Milnor方图，并由文献［10］的定理 2.2 知，An+1是几乎 Prüfer整环当且仅当An和Bn均是几乎 Prüfer整环，且qf(An)⊆Fn是根扩张.由于Bn是局部环，而局部的几乎Prüfer整环是几乎赋值整环.则An+1是几乎Prüfer整环当且仅当An是几乎 Prüfer整环，Bn是几乎赋值整环，qf(An)⊆Fn是根扩张.重复该结果，可得1)⇒2)和2)⇒1).

D.D.Anderson 等［2］给出了几乎 Bézout整环的概念，即设a，b∈R-{0}，存在某个正整数n，使得(an，bn)是主理想.于是有几乎Bézout整环在riding假设的条件下的反向极限也是几乎 Bézout整环.

推论2.4下述条件等价:

1)对每个n∈N，An是几乎Bézout整环；

2)A1是几乎 Bézout整环，且对每个n∈N，Bn是几乎赋值整环，qf(An)⊆Fn是根扩张；

3)A是几乎Bézout整环.

证明1)⇒2) 考虑强如图5所示的Milnor方图，并由文献［10］的定理2.9知，An+1是几乎Bézout整环当且仅当An和Bn均是几乎 Bézout整环，且qf(An)⊆Fn是根扩张.由于Bn是局部环，而局部的几乎Bézout整环是几乎赋值整环.则An+1是几乎Bézout整环当且仅当An是几乎Bézout整环，Bn是几乎赋值整环，qf(An)⊆Fn是根扩张.重复该结果，可得1)⇒2)和2)⇒1).

3)⇒1) 因为A是几乎Bézout整环且

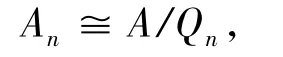
故An是几乎Bézout整环.

1)+2)⇒3) 因为A1≅A/Q1，Q1是A的除子素理想.由除子素理想的等价定义如图6所示的强Milnor方图.

图6

A是几乎Bézout整环当且仅当A1是几乎Bézout整环，AQ1是几乎赋值整环.所以要证明A是几乎Bézout整环，只需证明A1是几乎Bézout整环和AQ1是几乎赋值整环.由2)知，A1是几乎Bézout整环.由1)知，An是几乎 Bézout整环，从而An是几乎Prüfer整环，再由定理2.3 可得，A是几乎 Prüfer整环，于是有AQ1是几乎赋值整环，因此A是几乎Bézout整环.

3 几乎Prüfer整环的反向极限

在第2部分讨论了在 riding假设下，几乎Prüfer整环的反向极限是几乎 Prüfer整环.若去掉riding假设，则几乎Prüfer整环的反向极限未必是几乎 Prüfer整环.

例3.1存在一个反向系统

使得对每个n∈N，An是几乎 Bézout整环(因此也是几乎 Prüfer整环)，但是不是几乎Prüfer整环(因此也不是几乎 Bézout整环).

证明设存在一个整闭整环A(即设R是整环，Rc表示R在其商域K中的整闭包，若Rc=R，则称R是整闭整环)不是几乎Prüfer整环，且A的极小赋值扩环集{Vi|i∈N}是可数的.对每个n∈N，令

由文献［11］的定理107知，An是 Bézout整环(从而也是 Prüfer整环)，则An也是几乎 Bézout整环(从而也是几乎Prüfer整环).定义

如果n≥m，定义 φn，m:An→Am是包含映射，则{φn，m|n≥m}成为一个反向系统.但是它的反向极限

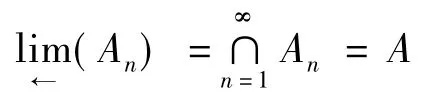
不是几乎Prüfer整环(也不是几乎Bézout整环).

建构一个具有上述性质的整环，设k是一个可数域，X是k上的未定元，且V=k(X)+M是有极大理想M的赋值整环，从而就是一个整闭的几乎赋值整环，则A=k+M是整闭的，但不是几乎Prüfer整环.

在例3.1中的反向系统{φn，m:An→Am|n≥m}缺乏一个重要条件，即φn，m不是满射.在第2部分后面的讨论中均设(An，φn，m:An→Am；n≥m)是一个反向系统，φn，m是满射.令

是标准映射，Qn=Ker(Φn)且Qn，m=Ker(φn，m)，其中n≥m.称此假设为弱riding假设.在弱riding假设下，下述引理3.2中的结果仍然成立.

引理3.21)对每个n∈N，Φn是满射；

2) 对每个n∈N，A/Qn≅An；

3) 如果r≥n，则

4) 如果r≥n∈N，则

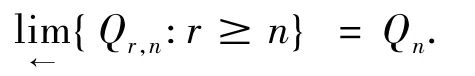
下面主要讨论，当An是一个几乎Prüfer整环时，是否有A是几乎 Prüfer整环.即对P∈Spec(A)，AP是否是几乎赋值整环.证明要求P包含某个Qk，这个条件在riding假设下自然成立，但是在弱riding假设下并不确保Qk⊆P.鉴于例3.1，首先应集中考虑An是一个几乎Bézout整环的情况.在这部分中，如果

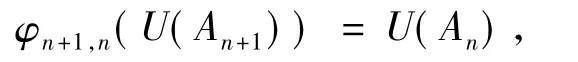
则定理3.3将给出一个肯定的结果.同第2部分中的结果对比，则定理3.3和推论3.4不需要下述条件:对每个n，Qn+1，n是An+1的除子素理想.

定理3.3设对每个n，An是几乎Bézout整环，且 φn+1，n诱导满射:U(An+1)→U(An).如果对P∈Spec(A)，使得对某个正整数k，Qk⊆P，则AP是几乎赋值整环.

证明对任意的α，β∈AP，只需证明，存在某个正整数t，使得 αt∈βtAP或 βt∈αtAP.由一般性，不妨设 α，β∈P，记

通过限制到(共尾)集{n∈N|n≥k}和对其进行重新标记，不妨取k=1，从而Q1⊆P，且对每个n≥1，

于是对所有的n，αn≠0和 βn≠0.因为An是几乎Bézout整环，所以An是几乎 GCD-整环(即设a，b∈R-{0}，存在某个正整数n，使得(an，bn)v是主理想.详情请参见文献［2］)，从而存在某个正整数t和dn∈An，使得

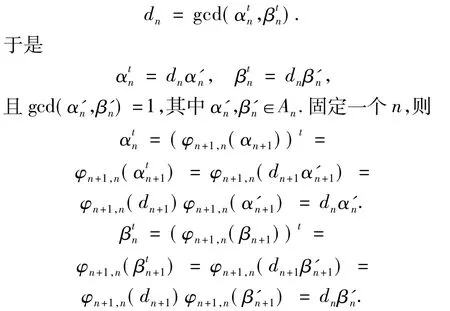
因为An+1是几乎Bézout整环，所以An+1是几乎GCD-整环，有

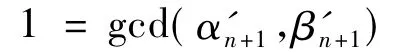
是 α'n+1与 β'n+1的线性组合，应用于 φn+1，n，则有

是 φn+1，n(α'n+1)与 φn+1，n(β'n+1)的线性组合.由文献［11］的定理49知

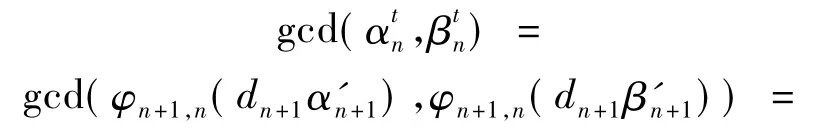
又因为的任何2个最大的共因子是相伴的，故存在 μn∈U(An)，使得 φn+1，n(dn+1)= μndn.

因为 φ2，1(U(A2))=U(A1)，重新定义d2以确保 φ2，1(d2)=d1，特别地d2=r2d2，其中r2∈U(A2)，满足 φ2，1(r2)= μ-1.用同样的方法重新定义d3，d4，…，以便对所有的n≥1，有 φn+1，n(dn+1)=dn.从而因为

推论3.4设对每个n，An是几乎Bézout整环，且 φn+1，n诱导满射:U(An+1)→U(An).如果对Spec(A)=∪{Im(Spec(An)→Spec(A))|n∈N}，则A是几乎Prüfer整环.

由文献［13］知，如果P是整环R的素理想，则R关于P的CPI-扩张是由下述拉回图:R(P)=RP×RP/PRPR/P所给出的一个整环.又由文献［12］的定理2.4、命题2.5和文献［9］的引理2.4知，PRP是R(P)的一个除子素理想.

设{φn，m:An→Am|n≥m}满足弱 riding 假设，定义反向系统是{φn，m}的相伴反向系统:如果对每个n≥2，设

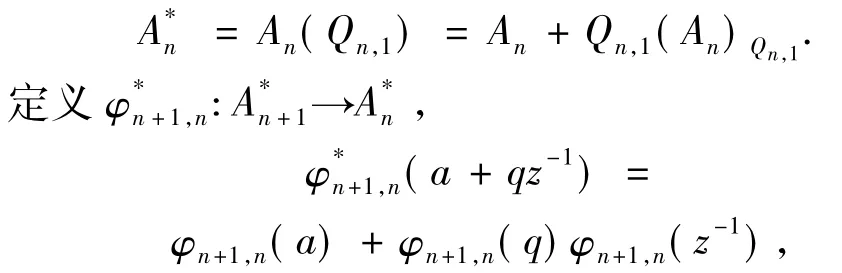
4 PVMD的反向极限

D.E.Dobbs等［1］提出可以考虑PVMD和GGCD整环在riding假设下的反向极限.因此，在这部分中讨论在riding假设下PVMD和G-GCD整环的反向极限.

为了本部分讨论的需要，现设K是R商域.所谓整环R上的星型算子指的是非零分式理想集合上的一个映射*:F(R)→F(R)，它满足以下性质:

1) 对任意A∈F(R)，a∈K-0有

(a)*=(a)，(aA)*=aA*；

2) 对任意A，B∈F(R)，若A⊆B，则有A*⊆B*；

3)对任意A∈F(R)，有A⊆A*，且(A*)*=A*.

对A∈F(R)，若A*=A，则A称为R的*-分式理想.若A是R的理想且A*=A，则A称为R的* -理想.设A∈F(R)，算子A→Av=(A-1)-1称为v-算子，而A→At=∪{Bv|B取遍A的所有有限生成子分式理想}是t-算子.关于另一类重要的w-算子，首先需知道Glaz-Vasconcclos理想(简称为GV-理想)的概念.即如果J是R的有限生成理想且J-1=R，则称J是GV-理想.于是对A∈F(R)，算子A→Aw={x∈K|Jx⊆A，对某个J∈GV(R)}是w-算子.

设I是R的分式理想，如果存在R的分式理想J，使得(IJ)w=R，则称I是R的w-可逆分式理想.如果R的每个有限生成理想是w-可逆的，则R称为PVMD(有关PVMD与星型算子的详细相关内容可参见文献［6-7］和［14-15］).若R的任意2个主理想的交仍是主理想，则R是GCD整环，GCD整环的推广类G-GCD整环是指:任意2个可逆理想的交仍是可逆理想.

命题4.1设RDTF是一个强Milinor方图，若R是PVMD，则M是T的t-理想.

证明假设M不是T的t-理想，因为M是T的极大理想，故Mt1=T，其中t1表示T上的t-算子.则存在一个有限生成理想

则I⊆M且IT=J，因此

T=M-1⊆I-1⊆(IT)-1=J-1=T，

故Iv=M.又因为R是一个 PVMD，则(a1，a2，…，ar)是w-可逆的，故I是w-可逆的，则M是w-可逆的.对任意x∈(M:M)，有xM⊆M，则x∈R，从而T⊆R，矛盾.所以M是T的t-理想.

引理4.2设R是整环，P是R的除子素理想，则P是w-理想.

证明因为P是R的除子素理想，故存在如图4所示的强Milnor方图，从而P=PRP是R的v-理想，也是R的w-理想.

定理4.3下述条件等价:

1)对每个n∈N，An是PVMD；

2)A1是PVMD，且对每个n∈N，Bn是赋值整环，qf(An)=Fn；

3)A是PVMD.

证明1)⇔2) 考虑如图5所示的强Milnor方图，由文献［16］的定理4.1知，An+1是PVMD当且仅当An和Bn均是PVMD，(Bn)Mn是赋值整环且qf(An)=Fn.又Mn为Bn的t-理想，从而为w-理想，故Mn是Bn的极大的w-理想.而w-局部的PVMD是赋值整环.则An+1是PVMD当且仅当An是PVMD，Bn是赋值整环，且qf(An)=Fn.重复该结果，可得1)⇒2)和2)⇒1).

3)⇒1) 因为Qn是A的除子素理想，故存在如图7所示的强Milnor方图.

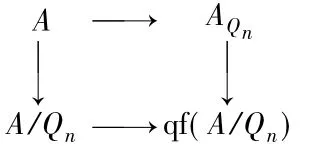
图7

而A是 PVMD，故A/Qn是 PVMD.又因为An≅A/Qn，所以An是 PVMD.

1)+2)⇒3) 因为A1≅A/Q1，Q1是A的除子素理想.由除子素理想的等价定义有如图6所示的强Milnor方图，A是PVMD当且仅当A1是PVMD，AQ1是赋值整环.所以要证明A是PVMD，只需证明A1是 PVMD和AQ1是赋值整环.由 2)知，A1是PVMD.由 1)知，当r≥1 时，有 Φr(Q1)=Qr，1，且对每个n∈N有

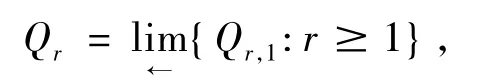
再由文献［1］的命题2.15知

而Qr，1是Ar的除子素理想，从而是素w-理想.又Ar是 PVMD，那么(Ar)Qr，1是赋值整环，由定理 3.1知，AQ1是赋值整环，从而A是PVMD.

推论4.4设RDTF是一个强Milinor方图，若R是G-GCD整环，则M是T的t-理想.

证明因为G-GCD整环是PVMD，由命题4.1知成立.

命题4.5设R是G-GCD整环，P是R的素理想，则R/P是G-GCD整环.

证明设x，y∈R/P，则存在a，b∈R，使得x=，y=.又因为R是G-GCD整环，有aR∩bR是可逆理想.而

故x¯R∩y是可逆理想，从而R/P是G-GCD整环.

定理4.6下述条件等价:

1)对每个n∈N，An是G-GCD整环；

2)A1是G-GCD整环，且对每个n∈N，Bn是赋值整环，qf(An)=Fn；

3)A是G-GCD整环.

证明1)⇔2) 考虑如图5所示的强Milnor方图，由文献［16］的定理4.2知，An+1是 G-GCD整环当且仅当An和Bn均是G-GCD整环，(Bn)Mn是赋值整环且qf(An)=Fn.又Mn为Bn的t-理想，故Mn是Bn的极大的t-理想.而Bn局部的GGCD整环是GCD整环，从而Bn是t-局部的GCD整环，则Bn是赋值整环.因此An+1是G-GCD整环当且仅当An是G-GCD整环，Bn是赋值整环，且

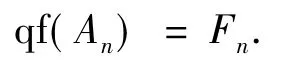
重复该结果，可得1)⇒2)和2)⇒1).

3)⇒1) 因为A是 G-GCD整环且An≅A/Qn，由命题4.5知，An是G-GCD整环.

1)+2)⇒3) 因为A1≅A/Q1，Q1是A的除子素理想.由除子素理想的等价定义有如图6所示的强Milnor方图，A是G-GCD整环当且仅当A1是G-GCD整环，AQ1是赋值整环.所以要证明A是G-GCD整环，只需证明A1是G-GCD整环和AQ1是赋值整环.由2)知，A1是G-GCD整环.因为An是G-GCD整环，从而An是PVMD，由定理4.3知，A是PVMD，又Q1是A的除子素理想，于是Q1是A的素w-理想，那么AQ1是赋值整环，所以有A是G-GCD整环.

［1］Dobbs D E，Fontana M.Inverse limits of integral domains arising from iterated nagata composition［J］.Math Scand，2001，88:17-40.

［2］Anderson D D，Zafrullah M.Almost Bézout domains［J］.J Algebra，1991，142:285-309.

［3］周霞，王芳贵.几乎Prüfer整环的研究［J］.四川师范大学学报:自然科学版，2007，30(3):330-334.

［4］周霞，王芳贵.几乎Prüfer整环的多项式环的维数和分式环［J］.四川师范大学学报:自然科学版，2010，33(4):437-442.

［5］Anderson D D，Knopp K R，Lewin R L.Almost Bézout Domains Ⅱ［J］.J Algebra，1994，167:547-556.

［6］王芳贵.交换环与星型算子理论［M］.北京:科学出版社，2006.

［7］王芳贵.星型算子理论的发展及其应用［J］.四川师范大学学报:自然科学版，2009，32(2):249-259.

［8］王芳贵.整环的赋值扩环及赋值维数［J］.四川师范大学学报:自然科学版，2010，33(4):419-425.

［9］Dobbs D E.Divided rings and going-down［J］.Pacific J Math，1976，67:353-363.

［10］Mimouni A.Prüfer-like conditions and pullbacks［J］.J Algebra，2004，279:685-693.

［11］Kaplansky I.Commutative Rings［M］.Chicago:Univ Chicago Press，1974.

［12］Monte B，Boisen J R，Sheldon P H.CPI-extensions:overrings of integral domains with special prime spectrums［J］.Can J Math，1997，4:722-737.

［13］Dobbs D E，Fontana M.On inverse limits of Bézout domains［J］.Abelian Groups，Rings，Modules，and Homological Algebra，2006，249:59-66.

［14］王芳贵.PVMD与自反模［J］.四川师范大学学报:自然科学版，2005，28(4):379-385.

［15］陈幼华，王芳贵，尹华玉.关于PVMD的一些刻画［J］.四川师范大学学报:自然科学版，2008，31(1):18-21.

［16］Fontana M，Gabelli S.On the class group and the local class group of a pullback［J］.J Algebra，1996，181:803-835.