正则剩余格的⊙理想拓扑空间

刘春辉

(1.赤峰学院教务处，内蒙古赤峰024001； 2.赤峰学院数学与统计学院，内蒙古赤峰024001)

1 引言及预备知识

对各种不同形式代数系统的研究是非经典数理逻辑［1］的一个重要的研究分支，适当的代数方法有效的推动了非经典数理逻辑理论的完善和发展［2-6］.在众多的逻辑代数系统中，由 M.Ward等［7］首次提出的剩余格是一类重要且应用广泛的代数系统，作为Heyting代数的合理推广，这一代数结构已经被学者们公认为较为理想的逻辑代数框架.迄今为止，人们已针对(正则)剩余格做了很多有意义的研究工作［8-13］，其中，文献［10］引入了正则剩余格的⊙理想概念，并对其特征和格论性质进行了细致的研究.文献［11］引入正则剩余格的生成⊙理想和素⊙理想概念，给出了它们的若干性质和等价刻画，并建立了正则剩余格的素⊙理想定理.在此基础上，本文运用拓扑学的概念和原理对正则剩余格的⊙理想概念作进一步深入研究.在给定正则剩余格上以全体⊙理想之集为基建立拓扑空间并讨论其拓扑性质，获得了一些有意义的结果.

为了讨论方便，首先介绍一些预备知识，有关拓扑学的概念和原理参见文献［14-15］.

定义1.1［7］设P是偏序集，称P上的二元运算⊗和→是互为伴随的，如果以下条件成立:

1)⊗:P×P→P是单调递增的；

2)→:P×P→P关于第一变量是不增的，关于第二变量是不减的；

3)a⊗b≤c当且仅当 a≤b→c，∀a，b，c∈P.此时称(⊗，→)为P上的伴随对.

定义1.2［7］设L是有最大元1和最小元0的有界格.若(⊗，→)是L上的伴随对且(L，⊗，1)是以1为单位元的交换半群，则称三元组(L，⊗，→)是剩余格或简称L是剩余格.

定义1.3［8］设L是剩余格，定义¬:L→L使∀a∈L，¬a=a→0，则称¬ 为 L上的伪补算子，如果∀a∈L都有¬¬a=a，则称L是正则剩余格.

在剩余格L上运算⊕和⊙定义为a⊕b=¬a→b，a⊙b=¬ (a→b)，∀a，b∈L.有关(正则)剩余格的性质以及⊙运算的性质参见文献［10-11］.

定义 1.4设(L1，⊗，→，¬ )和(L2，⊗，→，¬)是2个正则剩余格.称f:L1→L2是正则剩余格同态，如果对∀x，y∈L有 f(x∨y)=f(x)∨f(y)，f(x∧y)=f(x)∧f(y)，f(x⊗y)=f(x)⊗f(y)，f(x→y)=f(x)→f(y)，f(¬ x)= ¬ f(x).显然，若 f是正则剩余格同态，则f(0)=0且f(1)=1.

定义 1.5［10］设 L是剩余格，Ø≠I⊂L.如果∀a，b∈L 有0∈I且(b∈I和 a⊙b∈I)⇒a∈I，则称I是L的⊙理想.L的⊙理想全体之集记为I(L).

引理 1.1［10］设(L1，⊗，→，¬ ) 和(L2，⊗，→，¬)是2个正则剩余格，f:L1→L2是正则剩余格同态，则 I∈I(L1)→f(I)∈I(L2)且 I∈I(L2)⇒f-1(I)∈I(L1).

引理1.2［10］设L是正则剩余格，则 I∈I(L)当且仅当I为下集且对⊕运算封闭.

定义1.6［11］设L是正则剩余格，Ø≠A⊂L.称包含A的最小⊙理想为由A生成的⊙理想，记为〈A〉.特别地，当 A={a}时，〈{a}〉简记为〈a〉.

引理1.3［11］设L是正则剩余格且Ø≠A⊂L，则:

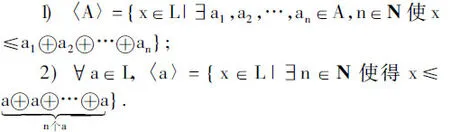
引理 1.4［11］设 L是正则剩余格，则∀x，y∈L，〈x〉∩〈y〉=〈x∧y〉.

2 ⊙理想拓扑空间的定义与基本性质

设L是一个正则剩余格，因为∀I，J∈I(L)，I∩J∈I(L)且∪{I|I∈I(L)}=L，所以由拓扑学的知识可知I(L)是L上某个拓扑的基.

定义2.1设L是正则剩余格，记L上以I(L)为基的拓扑为TL，称之为L上的⊙理想拓扑，并称拓扑空间(L，TL)为L的⊙理想拓扑空间.

例 2.1MV 单位区间［0，1］MV=(［0，1］，¬，→MV)，是特殊的正则剩余格，其中x→MVy=(1-x+y)∧1，则 I(［0，1］MV)={{0}，［0，1］}.因此［0，1］MV上以 I(［0，1］MV)为基的拓扑 TL={Ø，{0}，［0，1］}.

命题2.1设L是一个正则剩余格.∀x∈L，定义Bx={I∈I(L)|x∈I}，则Bx是x的一个关于拓扑TL的邻域基.

证明由文献［14］中定理2.6.7立即可得.

命题2.2设L是一个正则剩余格.定义B={〈x〉＞|x∈L}，则B也是L上⊙理想拓扑空间(L，TL)的一个基.

证明对∀I∈I(L)，易知，即I为集合{〈x〉|x∈L}中某些元素的并.又由引理1.4知B={〈x〉|x∈L}对交封闭，故B也是L上⊙理想拓扑空间(L，TL)的一个基.

命题2.3设L是正则剩余格.Ux为(L，TL)中点 x的邻域系，则〈x〉为(Ux，⊆)中最小元.

设L是正则剩余格，A⊆L，记A在(L，TL)中的导集、闭包和内部为d(A)、c(A)和i(A).

定理2.1设L是一个正则剩余格，A⊆L，则在L上的⊙理想拓扑空间(L，TL)中有d(A)={x∈L|〈x〉∩(A-{x})≠Ø}.

证明因为d(A)中包含A的全部聚点.而x∈L为A的聚点当且仅当∀U∈Ux都有U∩(A-{x})≠Ø，由命题2.3又知，这当且仅当〈x〉∩(A-{x})≠Ø，所以 d(A)={x∈L|〈x〉∩(A-{x})≠Ø}.

推论2.1设L是一个正则剩余格，则在L上的⊙理想拓扑空间(L，TL)中有:

1) ∀A⊆L，0∉d(A)；

2) ∀A∈I(L)，若 x∈A 且 x≠0，则x∈d(A)；

3)∀A⊆L，若0∈A，则0为A的孤立点.

定理2.2设L是正则剩余格，A⊆L，则A为(L，TL)中闭集⇔∀x∉A 且〈x〉∩A=Ø.

证明A为(L，TL)中闭集⇔d(A)⊆A⇔∀x∈L，〈x〉∩(A-{x})≠Ø 蕴涵 x∈A⇔x∉A 且〈x〉∩(A-{x})=Ø⇔x∉A 且〈x〉∩A=Ø.

推论2.2设L是一个正则剩余格.若0∈A⊆L，则 A 不是(L，TL)中闭集.

证明因为A⊆L，所以∃x∈L使x∉A且〈x〉∩A≠Ø.故A不是(L，TL)中闭集.

定理2.3设L是一个正则剩余格，A⊆L，则在L上的⊙理想拓扑空间(L，TL)中有c(A)=∩{L-〈x〉|x∈L，〈x〉∩A= Ø}.

证明因为在一个拓扑空间中，集合A的闭包等于包含A的所有闭集的交，所以再结合命题2.2可得x∈BU⊆L，U∈TL}=∩{L-〈x〉|〈x〉∩A=Ø}.

定理2.4设L是一个正则剩余格，A⊆L，则在L上的⊙理想拓扑空间(L，TL)中有i(A)=∪{〈x〉|x∈L，〈x〉⊆A}.

证明i(A)=∪{U|U⊆A，U∈TL}=∪{〈x〉|〈x〉⊆A，x∈BU⊆L，U∈TL}= ∪{〈x〉|x∈L，〈x〉⊆A}.

推论2.3设L是一个正则剩余格，A⊆L，则在L上的⊙理想拓扑空间(L，TL)中有:

1) 若0∈A，则c(A)=L；

2)若0∉A，则i(A)=Ø.

3 ⊙理想拓扑空间(L，TL)的拓扑性质

讨论(L，TL)的连续映射、紧致性、连通性、可数性、分离性等拓扑性质.

定理 3.1设(L1，⊗，→，¬ )和(L2，⊗，→，¬)是2个正则剩余格，f:L1→L2是正则剩余格同态，则 f是拓扑空间(L1，TL1)到拓扑空间(L2，TL2)的连续映射.

证明由引理1.1和文献［14］中定理2.6.5立即可得.

定理3.2设L是一个正则剩余格，则L上的⊙理想拓扑空间(L，TL)是紧致空间.

证明设A={Iα|α∈Λ}⊆I(L)是 L的开覆盖，即，则由 1∈L 知存在 α0∈Λ 使 1∈Iα0.从而由 I∈I(L)为下集得 I=L，因此{Iα0}为 L的开覆盖A的一个有限子覆盖，故(L，TL)是紧致空间.

定理3.3设L是一个正则剩余格，则L上的⊙理想拓扑空间(L，TL)是连通空间.

证明设U是L的既开又闭的非空真子集，则存在{Iα|α∈Λ}⊆I(L)使，所以 0∈U.但另一方面，因为也是(L，TL)中开集，所以又∃I∈I(L)使0∈I⊆LU，这矛盾于0∈U.因此L中不存在既开又闭的非空真子集，从而(L，TL)是连通空间.

定理3.4设L是一个正则剩余格，则(L，TL)满足第I可数性公理，即(L，TL)是A1空间.

证明因为由命题2.2知，∀x∈L，{〈x〉}为点x的一个邻域基，所以(L，TL)满足第I可数性公理，即(L，TL)是 A1空间.

定理3.5设L是一个正则剩余格，则(L，TL)满足第II可数性公理，即(L，TL)是A2空间当且仅当{〈x〉|x∈L}是可数集.

证明若{〈x〉|x∈L}是可数集，则由命题2.2知(L，TL)满足第II可数性公理.反之，设(L，TL)满足第II可数性公理，则(L，TL)有一个可数基，设为B={B1，B2，…，Bn，…}于是任取 x∈L，∃Bi∈B 使x∈Bi，从而 Bi∈Ux.故由命题 2.3 知〈x〉⊆Bi，因此|{〈x〉|x∈L}|≤|B|，所以{〈x〉|x∈L}是可数集.

定理3.6设L是一个正则剩余格，则(L，TL)是T0空间当且仅当∀x∈L，x⊕x=x.

证明设∀x∈L，x⊕x=x，则由引理1.3的2)得〈x〉={y∈L|y≤x}.于是，任取 x，y∈L 且 x≠y，则当 x与y不可比较大小时，x∉〈y〉且 y∉〈x〉；当x与 y可以比较大小时，不妨设 y＜x，则 x∉〈y〉.故由命题2.2知(L，TL)是 T0空间.反之，设(L，TL)是 T0空间，若∃x∈L 使 x⊕x≠x，则 x∈〈x⊕x〉且 x⊕x∈〈x〉，矛盾! 故∀x∈L，x⊕x=x.

定理3.7设L是一个正则剩余格，则(L，TL)既不是T1空间也不是T2空间.

证明因为∀U∈TL都有0∈U，从而L-{0}不是(L，TL)中开集，故单点集{0}不是(L，TL)中闭集，所以(L，TL)不是T1空间，从而也不是T2空间.

定理3.8设L是一个正则剩余格，则(L，TL)既不是正则空间也不是正规空间.

证明因为(L，TL)中任意2个非空开集都相交，所以(L，TL)既非正则也非正规空间.

4 积空间

定义 4.1设(Li，⊗i，→i，¬i)，i∈J 是一族正则剩余格.令，在L上点式的定义二元运算⊗，→和一元运算¬，则(L，⊗，→，¬)构成一个正则剩余格，称为乘积正则剩余格.

设(L1，⊗，→，¬ )和(L2，⊗，→，¬ )是 2 个正则剩余格，TL1和TL2分别为L1和L2上的⊙理想拓扑.若令 L=L1×L2，一方面，由 TL1和 TL2可自然地在L上诱导一个乘积拓扑T=TL1×TL2，且T以B={U1×U2|U1∈TL1，U2∈TL2}为基.另一方面，由定义4.1知，L=L1×L2也是正则剩余格，故在L上也可按定义2.1的方式定义⊙理想拓扑TL，且TL以I(L)=I(L1×L2)为基.一个自然的问题是:L上乘积拓扑T与⊙理想拓扑TL之间关系如何?

定理 4.1设(L1，⊗，→，¬ )和(L2，⊗，→，¬)是2个正则剩余格，L=L1×L2为乘积正则剩余格，则对∀I1∈I(L1)和 I2∈I(L2)，都有 I=I1× I2∈I(L).反之，L的任一⊙理想都具有如上形式，即I(L)={I1×I2|I1∈I(L1)，I2∈I(I2)}.

证明任取I1∈I(L1)和I2∈I(L2)，令I=I1×I2.由0∈I1且 0∈I2得(0，0)∈I1× I2=I.设(x2，y2)∈I且(x1，y1)⊙(x2，y2)∈I，即(x2，y2)∈I且(x1⊙x2，y1⊙y2)∈I，则 x2，x1⊙x2∈I1且 y2，y1⊙y2∈I2，故由 I1∈I(L1)和 I2∈F(L2)得 x1∈I1且 y1∈I2，从而(x1，y1)∈I，因此 I∈I(L).

反之，任取 I∈I(L)，令 I1={x∈L1|∃y∈L2，(x，y)∈I}且 I2={y∈L2|∃x∈L1，(x，y)∈I}，则由(0，0)∈I知 0∈I1且 0∈I2.任取 x1，x2∈L1，x2，x1⊙x2∈I1，则∃y1，y2∈L2使(x2，y2)∈I 且(x1⊙x2，y1)∈I.注意到 I为下集便得(x2，0)∈I且(x1⊙x2，0)∈I，即(x2，0)∈I且(x1，0)⊙(x2，0)∈I，从而(x1，0)∈I，故 x1∈I1.因此 I1∈I(L1).类似可证 I2∈I(L2).下证 I=I1×I2.显然 I⊆I1× I2.设(x，y)∈I1× I2，则 x∈I1且 y∈I2，故由前面的证明知(x，0)，(0，y)∈I.又(x，0)⊙(x，y)=(x⊙x，0⊙y)=(0，y)∈I，所以由 I∈IL(L)得(x，y)∈I，因此 I1×I2⊆I，从而 I=I1×I2.

定理 4.2设(L1，⊗，→，¬ )和(L2，⊗，→，¬)是2个正则剩余格，L=L1×L2为乘积正则剩余格，则L上乘积拓扑T与⊙理想拓扑TL是一致的，即T=TL.

推论 4.1设(Li，⊗，→，¬ )，i∈J为一族正则剩余格，为乘积正则剩余格，则L上乘积拓扑与⊙理想拓扑TL是一致的，即.

［1］王国俊.非经典数理逻辑与近似推论［M］.北京:科学出版社，2000.

［2］王国俊.MV-代数，BL-代数，R0-代数与多值逻辑［J］.模糊系统与数学，2002，16(2):1-15.

［3］Xu Y，Ruan D，Qin K Y，et al.Lattice-valued Logic［M］.Berlin:Springer-Verlag，2004.

［4］张小红.模糊逻辑及其代数分析［M］.北京:科学出版社，2008.

［5］朱怡权.关于PFI代数的格论性质［J］.四川师范大学学报:自然科学版，2007，30(2):181-184.

［6］Liu C H，Xu L S.Prime MP-filter spaces of fuzzy implication algebras［J］.China Quart J Math，2012，27(2):246-253.

［7］Ward M，Dilworth R P.Residuated lattices［J］.Trans Am Math Soc，1939，45:335-354.

［8］裴道武.剩余格与正则剩余格的特征［J］.数学学报，2002，45(2):271-278.

［9］刘春辉，徐罗山.关于剩余格的理想［J］.山东大学学报:理学版，2010，45(4):66-71.

［10］Liu C H，Xu L S.On ⊙ -ideals and lattices of⊙ -ideals in regular residuated lattices［J］.Adv Intel Soft Comput，2010，82:425-434.

［11］刘春辉，徐罗山.正则剩余格的生成⊙理想与素⊙理想［J］.四川师范大学学报:自然科学版，2010，33(5):621-625.

［12］秦学成，刘春辉.正则剩余格的Fuzzy⊙理想［J］.山东大学学报:理学版，2010，45(10):66-70.

［13］秦学成，刘春辉.正则剩余格的Fuzzy⊙理想格［J］.山东大学学报:理学版，2011，46(8):73-76.

［14］熊金成.点集拓扑学讲义［M］.北京:科学出版社，2003.

［15］Kelley J L.General Topology［M］.New York:Springer-Verlag，1991.