广义不完备直觉模糊信息系统的属性约简

杨柳娇，舒 畅，莫智文*

(1.四川师范大学数学与软件科学学院，四川成都610066； 2.成都理工大学管理科学学院数学教学系，四川成都610059)

模糊集理论［1］是美国学者Zadeh在1965年提出的一种处理不精确和不确定问题的强有力数学工具，随着模糊集理论的发展，Zadeh模糊集只考虑隶属度一个方面的信息已不能满足实际需要.为此对Zadeh模糊集进行拓展，保加利亚学者Atanassov综合考虑了隶属度，非隶属度和犹豫度3个方面的信息，于1983年提出了直觉模糊集［2］的概念，并被广泛应用于决策，模式识别，数据挖掘等许多领域.

不完备信息系统是指信息系统中出现了未知属性值［3-7］，不完备信息系统中的未知属性值可以从两种不同的语义来解释.第一是所有的未知属性值被认为是丢失的，是不允许被比较的:第二是所有的未知属性值仅仅是被遗漏的，但又是确实存在的.目前为止，很多学者只考虑不完备信息系统中仅有一种可能的解释而没有考虑遗漏型和丢失型未知属性值共存的情况，文献［8］中将这种不完备系统称为广义不完备信息系统.

目前，对直觉模糊信息系统的研究甚少.文献［9］对基于优势关系对完备直觉模糊信息系统与决策信息表的属性约简问题进行了研究.谢海等［10］对文献［9］中的优势关系进行扩充进而讨论了基于广义优势关系得到了不完备直觉模糊信息系统与决策信息表的属性约简和相对约简［10］.但文献［10］只讨论了系统中未知属性值丢失的情况并未讨论系统中属性值遗漏和某一属性值中部分丢失共存的情况，故本文给出广义不完备直觉模糊信息系统的定义，并对系统作完备化处理，引入特征关系再作研究.

1 广义不完备直觉模糊信息系统

不完备直觉模糊信息系统中的基本概念如下:

定义1.1［1］论域U上的模糊集A定义为:A={〈x，μA(x)〉|x∈U}，其中 μA:U→［0，1］是A的隶属函数，μA(x)∈［0，1］是x属于A的隶属度.

定义1.2［2］论域U上的直觉模糊集A定义为:A={〈x，μA(x)，νA(x)〉|x∈U}，其中 μA(x)称为x属于A的隶属度，νA(x)称为x不属于A的隶属度，并且满足关系式0≤μA(x)+νA(x)≤1.称πA(x)=1-μA(x)-νA(x)为x属于A的犹豫度或不确定度，显然 πA(x)∈［0，1］，∀x∈U.

定义 1.3［9］称一个四元组S=(U，AT，V，f)为信息系统，其中U为有限非空对象集；AT为有限非空属性集；V为属性值值域；f为对象属性值映射，即U={x1，x2，…，xn}，AT={a1，a2，…，an}，V=∪Va，a∈AT，Va为属性a的值域，f:U×AT→V，且f(x，a)∈Va.若Va的每个元素均为直觉模糊对，即对∀x∈U，a∈AT，都有f(x，a)=(μa(x)，νa(x))，则称该信息系统为直觉模糊信息系统.若μa(x)=1-νa(x)，则该信息系统退化为一般的信息系统.

定义1.4［10］在定义3中，对某些对象而言，其所对应的一些属性值可能会存在缺省的情况，将缺省的属性值称为空值，并用“*”表示空值.如果至少有一个属性a∈AT，使得Va含有空值，则称此系统为不完备直觉模糊信息系统.

为了使信息系统更接近现实的详细情况，给出下面的定义:

定义1.5广义不完备直觉模糊信息系统有4种情况:

1)f(x，a)=(*，νa(x))不知道x属于A的隶属度.

2)f(x，a)=(μa(x)，*)不知道x不属于A的隶属度.

3)f(x，a)=(*，*)不知道x属于A的隶属度，也不知道x不属于A的隶属度.

4)f(x，a)=?属性值是丢失的，不允许被比较.

例1.1表1给出一个广义不完备直觉模糊信息系统.

表1 广义不完备直觉模糊信息系统Table 1 Generalized incomplete intuitionistic fuzzy information system

对于上面的不完备直觉模糊信息系统显然不能用一般的关系来处理，需要建立针对缺失值“*”和遗漏值“?”的关系，这种关系称为特征关系.设S=(U，AT，V，f)为广义不完备直觉模糊信息系统，针对上面出现的4种情况作如下处理:

1)f(x，a)=(*，νa(x))，* =(1- νa(x))∧max(μa(xi)).

2)f(x，a)=(μa(x)，*)，* =(1- μa(x))∧min(νa(xi)).

3)f(x，a)=(*，*)，(*，*)=(max(μa(xi))，(1-max(μa(xi)))∧min(νa(xi))).

4)f(x，a)=?.

这样表1就可以转变为表2.

定义 1.6［11］记L={(x1，x2)∈［0，1］×［0，1］|0≤x1+x2≤1}，格(L，≤L)上的序关系≤L定义为(x1，x2)≤L(y1，y2)⇔x1≤y1，x2≥y2.

定义1.7［10］在直觉模糊信息系统中，如果f(x，a)≥Lf(y，a)，就说x关于a占优于y，记作x≻ay.

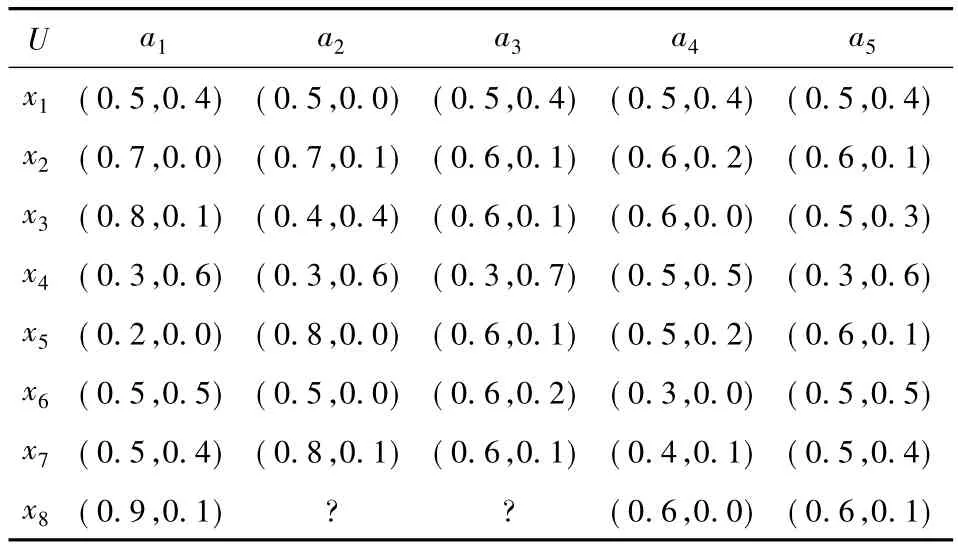
表2 广义不完备直觉模糊信息系统Table 2 Generalized incomplete intuitionistic fuzzy information system

结合以上情况给出广义不完备直觉模糊信息系统中的特征关系如下:

定义1.8设S=(U，AT，V，f)为广义不完备直觉模糊信息系统，对于A⊆AT，称

为广义不完备直觉模糊信息系统的特征关系.

此关系认为如果论域中的2个元素对应的属性值除含有丢失值的外都满足x≻ay，那么就将这两元素划分为一类.

显然，此特征关系满足自反性，传递性，但不满足对称性.

2 广义不完备直觉模糊信息系统基于特征关系的属性约简

定义2.1设S=(U，AT，V，f)为一个广义不完备直觉模糊信息系统，若A⊆AT，LRA=LRAT，且LRB≠LRA，∀B⊆A，则称A是S的一个约简.

定义2.2设S=(U，AT，V，f)为一个广义不完备直觉模糊信息系统，称

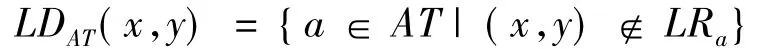
为在特征关系下可辨识x与y的属性集，矩阵LDAT={LDAT(x，y)|x，y∈U}称为该广义不完备直觉模糊信息系统的辨识矩阵.

定理2.1设S=(U，AT，V，f)为一个广义不完备直觉模糊信息系统，则A是约简集⇔∀(x，y)∉LRAT，则有A∩LDAT(x，y)≠Ø.显然，由约简的定义和辨识矩阵的定义易得此定理成立.

定义2.3设S=(U，AT，V，f)为一个广义不完备直觉模糊信息系统，称为该广义不完备直觉模糊信息系统的辨识公式.

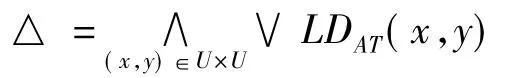
表3 广义不完备直觉模糊信息系统的辨识矩阵Table 3 Discernibility matrix of generalized incomplete intuitionistic fuzzy information system

例2.1表1的辨识矩阵如表3所示.

由定义2.3可得上表的辨识公式△=a1∧a2∧a4.因此该广义不完备直觉模糊信息系统约简为a1，a2，a4.

3 广义不完备直觉模糊决策信息系统基于特征关系的属性约简

定义3.1设S=(U，AT∪d，V，f)为一个广义不完备直觉模糊信息系统，其中AT为条件属性集，d为决策属性，且AT∩d=Ø，f(x，d)为单值的有序实值.记LDd={(x，y)|f(x，d)≥f(y，d)}，如果LRAT⊆LDd，则称该决策信息系统是协调的，否则是不协调的.

表4 协调广义不完备直觉模糊决策信息系统Table 4 Coordinational generalized incomplete intuitionistic fuzzy decision information system

例3.1如表4 所示，设S=(U，AT∪d，V，f)为一个广义不完备直觉模糊决策信息系统，且

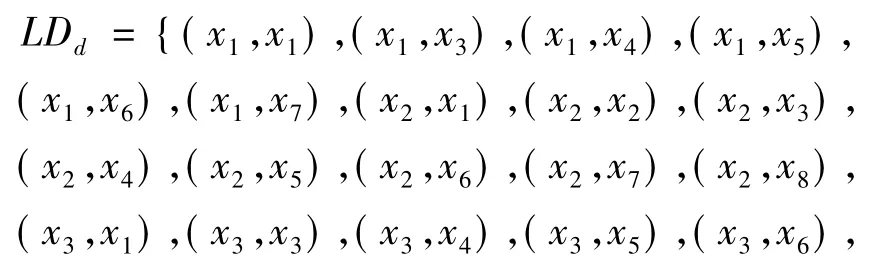
显然LRAT⊆LDd，所以该决策信息系统为一个协调的广义不完备直觉模糊决策信息系统.

定义3.2设S=(U，AT∪d，V，f)为一个协调广义不完备直觉模糊决策信息系统，若A⊆AT，LRA⊆LDd，且LRBLDd，∀B⊆A，则称A是决策信息系统S的一个相对约简.

定义3.3设S=(U，AT∪d，V，f)为一个协调广义不完备直觉模糊决策信息系统，称

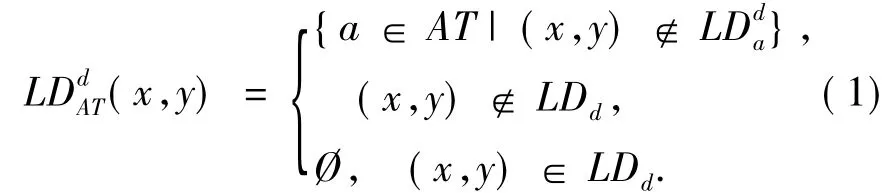
为可辨识x与y的属性集，矩阵称为该决策信息系统的辨识矩阵.

定理3.1设S=(U，AT∪d，V，f)为一个协调的广义不完备直觉模糊决策信息系统，则A是约简集⇔∀(x，y)∉LDd，则有

显然，由约简的定义和辨识矩阵的定义易得此定理成立.

定义3.4设S=(U，AT∪d，V，f)为一个协调的广义不完备直觉模糊决策信息系统，称

为该决策信息系统的辨识公式.

例3.2计算表4的辨识矩阵如表5所示.

表5 协调广义不完备直觉模糊决策信息系统的辨识矩阵Table 5 Discernibility matrix of coordinational generalized incomplete intuitionistic fuzzy decision information system

由定义3.4可得上表的可辨识公式△=a1，即该决策信息系统的相对约简为a1.

4 结语

本文将文献［10］中的不完备直觉模糊信息系统拓展为广义不完备直觉模糊信息系统，它的未知属性值有4种情况，因而更具有代表性.引入特征关系分别讨论了广义不完备直觉模糊信息系统和协调广义不完备直觉模糊决策信息系统的属性约简和相对约简.下一步的工作是对不协调广义不完备直觉模糊决策信息系统的进一步研究.

［1］ZadehL A.Fuzzy sets［J］.Information and Control，1965(8):338-353.

［2］Atanassov K T.Intuitionistic fuzzy sets［C］//Polish Symp Interval Fuzz Math.Pozana，1983(8):23-26.

［3］颜艳，丁健，管雪珍.不完备信息系统的一种属性约简［J］.计算机工程与应用，2010，46(36):165-167.

［4］曾晓辉，文展.不完备信息系统的属性约简算法［J］.计算机工程，2009，35(24):185-187.

［5］魏利华，唐振民，丁辉，等.不完备区间值信息系统的促进理论［J］.信息与控制，2009，38(3):286-292.

［6］Dembczynski K.Rough set approach to multiple criteria classification with imprecise evaluations and assignments［J］.Euro J Oper Research，2008，198(2):63-83.

［7］赵亮，张欣，薛质.不完备区间值信息系统的安全评估［J］.计算机工程，2011，37(11):146-148.

［8］周靖.广义不完备系统中的知识约简［J］.计算机工程与应用，2008，44(28):149-151.

［9］杜文胜，胡宝清，赵彦.基于优势关系的直觉模糊集信息系统上的属性约简［J］.运筹与模糊学，2011(1):1-5.

［10］谢海，胡宝清.不完备直觉模糊信息系统属性约简［J］.数学的实践与认识，2012，42(19):210-217.

［11］Kusunoki Y，Inuiguchi M.A comprehensive study on reducts in dominance-based rough set approach［C］//Torra V，Narukawa Y.MDAI，LNAI，5285.2008:167-178.