关于二项指数和的均值

郑家兵，廖群英

(四川师范大学数学与软件科学学院，四川成都610066)

1 引言及主要结果

1993 年，F.Smararadche［1］提出了许多数论问题，引起了国内外相关学者的关注.迄今为止，针对Smararadche问题，有很多有趣的均值及相应的渐近公式［1-4］，利用这些函数的均值及渐进公式可以为工程或其它方面的需要进行估值.指数和的均值计算是其中很重要的问题之一.

早在1976年，著名数论专家华罗庚给出了经典指数和的定义［5］，即:对任意正整数q以及整系数多项式f(x)∈Z［x］{0}，关于q和f(x)的指数和定义如下

给定奇素数p和整数b、m以及n，满足m≥2，n≥2 且(n(n-1)b，p)=(n-1，p-1)=1，则对任意整数a，文献［6］给出了f(x)=axn+bx，q=pm时s(f，q)的一个上界，即

定义1［7］设m、n为整数且q及k为正整数，χ为模q的狄利克雷特征，则复合指数和定义为

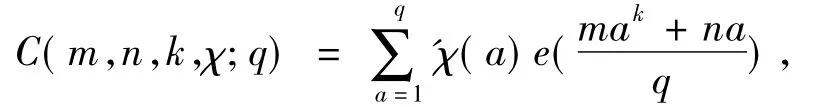
其中，e(y)=e2πyi，为对所有满足(a，q)=1的正整数a求和.

定义 2［8］设m、n为整数且q、k、h为正整数，则二项指数和定义如下

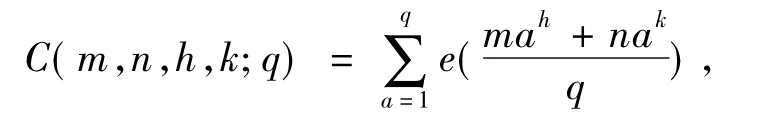
其中e(y)=e2πyi.

文献［9］曾对特殊的指数和，即广义k次高斯和

的均值进行了研究.进而，对任意给定正整数q及k，满足(k，q)=1，则对任意正整数n，文献［7］证明了当(n，q)=1 时有

其中，φ(q)为欧拉函数，表示对q的所有满足pα|q而pα+1q的素因子p求积.

关于二项指数和的讨论及应用可参见文献［10-15］，其中涉及到的一个主要问题是计算

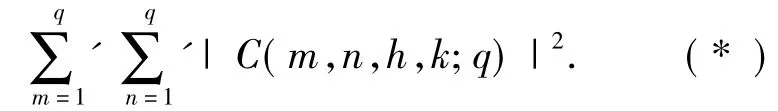
定理1设正整数，其中pi为不同素数，αi≥1，则有

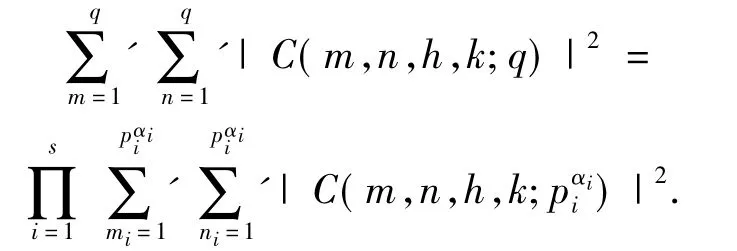
由定理1，(*)式的计算问题转化为计算二项指数和C(m，n，h，k；q)在q为素数p的方幂pα情形下的均值.最近，文献［2］给出了:当q为奇素数p且k=h-2，α=1时，(*)式的如下渐进公式

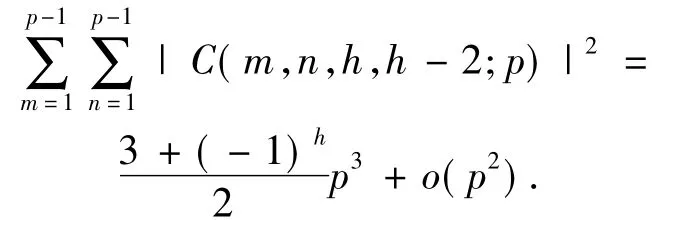
本文进一步研究(*)式的均值，给出了当q=pα(α≥1)时不同情形下(*)式均值的准确计算公式.

定理2给定奇素数p以及正整数k和h，且(hk，p)=1，则有

其中，d1=(h，p-1)，d2=(k，p-1)，d3=(d1，d2).

推论1给定奇素数p及正整数h和k，当k|h及(h，p)=1 时有

定理3若素数p≡5，11(mod 12)，正整数k≥2 且(k，p)=1，d=(k，p-1)，则有

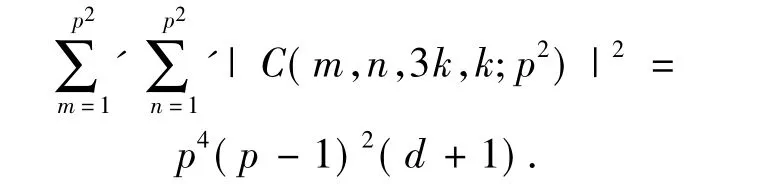
定理4设p为奇素数，h和α为正整数且h≥α，则有

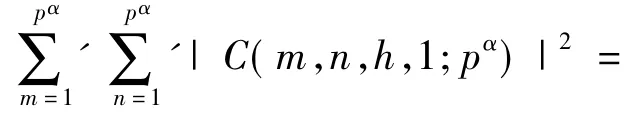
注1本文的定理2～4考虑的是q为素数方幂的情形，其中，定理1讨论了q为奇素数p时的均值，而文献［2］中的结果加了k=h-2的限制，定理1是文献［2］的推广.在定理1的基础上，要计算(*)式的均值，还存在很大的难度.于是，考虑缩小范围，得出一些更为逼近的结论:限制q的范围以及h=3k，利用同余方程知识求其均值，即定理3；取k=1利用解析方法得到定理4.定理3与定理4的方法不一样，可以为学者们提供解决(*)均值的思路.

2 主要结果的证明

引理 1设素数p≡5，11(mod 12)，则f(x)=x3-1-kp≡0(modp2)有整数解当且仅当有整数解.

即f(x)≡(modp2)有整数解x.

又因为满足pα-1|(a-1)的a只能取1，pα-1+1，2pα-1+1，…，(p-1)pα-1+1.把a=ipα-1+1，i=0，1，2，…，p-1，代入ah-1 可知要使pα|(ah-1)成立，只需满足pα|hipα-1.当(h，p)=1 时，只能a=1；否则，a=1，pα-1+1，2pα-1+1，…，(p-1)pα-1+1均可，即

于是由(8)式及(12)和(13)式可知，当(h，p)=1时有

注2在定理4中取p≡5，11(mod 12)，h=3且α=2，还可以仿照定理3的证明得到

［1］Smararadche F.Only Problems，Not Solutions［M］.Chicago:Xiquan Publishing House，1993.

［2］徐哲峰.一些新的数论函数及其均值公式［J］.数学学报，2006，49(1):77-80.

［3］郑家兵，廖群英.关于正整数n的r次可加补数［J］.四川师范大学学报:自然科学版，2013，36(3):324-327.

［4］Xu Z F.On the additivek-power complement［C］//Researh on Smararadche Problems in Number Theory.Phoenix:Hexis，2004.

［5］Hua L K.On exponential sums［J］.Sci Record，1957，1:1-4.

［6］Cochrane T，Zheng Z Y.Bounds for certain exponential sums［J］.Asian J Math，2000，4(4):757-774.

［7］Liu H N.Mean value of mixed exponential sums［J］.Proc Am Math Soc，2008，136(4):1193-1203.

［8］Wang T T，Pan X W.The mean value involving Dedekind sums and two-term exponential sums［J］.Science in China，2012，55(3):557-565.

［9］He Y，Liao Q Y.On the mean value of generalk-th Gauss sums［J］.J Math Research Appl，2011，3(6):1009-1014.

［10］Apostol M T.Introduction to Analytic Number Theory［M］.New York:Springer-Verlag，1976:157-162.

［11］Cochrane T，Piner C.A further refinement of mordell's bound on exponential sums［J］.Acta Arith，2005，116:35-41.

［12］Cochrane T.Using stepanov's method for exponential sums involving rational functions［J］.J Number Theory，2006，116:270-292.

［13］Zhang T P.On mixed two-term exponential sums［J］.J Korean Math Soc，2010，47(6):1107-1122.

［14］Yang P，Cai T X.On the divisibility of multinomial exponent sums［J］.Adv Math(China)，2014，43(3):387-397.

［15］Li J H，Zhang W P.A hybrid mean value involving the Dedekind sums and exponential sums［J］.Adv Math(China)，2014，43(4):527-533.