我国28个省、市、自治区社会经济发展的多元统计分析——基于2012年统计数据

史亚楠

（西北师范大学 经济学院，甘肃 兰州730070）

我国28个省、市、自治区社会经济发展的多元统计分析
——基于2012年统计数据

史亚楠

（西北师范大学 经济学院，甘肃 兰州730070）

通过主成分分析、因子分子对我国28个省、市、自治区的8项社会经济发展指标数据，旨在提取能近似且具有综合性解释社会经济发展的主因子成分，以据此对各地区社会经济发展状况进行分类、比较和综合排序评价。

经济发展；主成分分析；因子分析；综合评价

本文选取了其中28个省 （其他三省的数据留待判别分析时使用）的8项指标来综合评价各地的经济发展状况：GDP（单位：亿元）、居民消费水平（单位：元）、固定资产投资（单位：亿元）、职工平均工资（单位：元）、货物周转量（单位：元）、居民消费价格指数（单位：%）、商品零售价格指数（单位：%）、工业总产值（单位：亿元）。为了保证分析结果的有效性，需要将量纲不同的各指标值标准化。

一、检验待分析的原始变量是否适合作因子分析

因子分析的重要前提是要求原始变量具有较强的相关性。经过计算相关系数矩阵后得得出，本文所选取的八个变量之间存在显著的相关性，且通过了检验，可以进行主成分分析和因子分析。

为了保证分析结果的有效性，在这里运用巴特利特球体检验 （Bartlett’s test of sphericity）对所选指标进行再次检验。由检验结果可知，统计量的值比较大，为175.569，其对应的伴随概率值小于预先给定的显著性水平（α=0.05）。所以认为与原始变量之间存在相关性，数据适合做因子分析。

二、运用主成分分析法提取公因子

一般而言，当分析中所选择的变量具有不同的计量单位，或变量水平差异很大时，应该选择基于相关系数矩阵的主成分分析。否则，基于协方差阵作主成分分析效果可能更好。本文选择用相关阵作分析。

做出变量共同度，从表中可以看出，除货物周转量和居民消费价格指数的共同度较低外，其余指标的共同度都大于0.85，表明提取的主成分对每个变量的解释程度都较高。利用相关阵求得的特征根及对应标准化特征向量如表1所示。

表1：总方差解释（Total Variance Explained）

由表1可以看出，SPSS提取了三个主成分，其特征根的值均大于1。第一个主成分的特征根为3.852，方差贡献率为48.149%，第二个主成分的特征根为1.377，方差贡献率为17.212%，第三个主成分的特征根为1.336，方差贡献率为16.696%，三个主成分的累计方差达到82.058%，即三个主成分共解释了总变异的82.058%，进一步说明提取的三个主成分是比较合适的。

由碎石图选择主成分也可得到相同的结果。碎石图是以主成分为横坐标，特征根为纵坐标的图形。根据本文所选数据做出的碎石图如图1所示。

图1

实际上，碎石图就是按特征根大小排列的主成分折线图。图1在第四个特征根处变得比较平缓，表明可以提取三个主成分。

三、旋转公因子并进行因子命名

因子载荷矩阵中的数值是主成分与原始变量的相关系数，绝对值的大小代表了主成分与原始变量的相关程度，据此可以看出每一主成分所代表的原始变量的信息。提取的主成分在变量之间的载荷有时相差不大，所以无法明确解释各个主成分所代表的信息，也就无法进行因子命名。因此，必须进行因子旋转。

表2：旋转后的总方差解释

由表2可以发现：前三个公因子的累计贡献率相同（均为82.058%），但每个公因子的特征根发生了变化，其贡献率也发生了变化。由此看来，因子旋转相当于在确定公因子数目的前提下，将共同的累计贡献率在各个公因子上重新分配。

表3：旋转后的因子载荷矩阵

由表3可以看出，因子1在GDP、固定资产投资、工业总产值、货物周转量这四个变量上有较大载荷，所以因子1主要反映了这四个变量的信息，可命名为“经济发展总量因子”；因子2在居民消费水平和职工平均工资上有较大载荷，可命名为“消费因子”；因子3在居民消费价格指数和商品零售价格指数上有较大载荷，可命名为“价格因子”。

四、计算因子得分

运用SPSS得出因子得分系数矩阵后，将系数代入因子得分函数，所以综合指标体系的因子得分函数为：

运用SPSS得到了“fac1_1”、“fac2_1”、“fac3_1”三列数据，即为因子得分值，将其储存，运用在后边的综合比较排序中。

五、从各个主因子的得分排名看各省市的经济发展情况

表4为所选取的28个省、市、自治区的因子得分排名情况。

第一主因子（即经济发展总量因子）得分较高的省市主要有：广东、江苏、山东、浙江、上海、河南、辽宁、河北、湖北、湖南。从这项结果，我们不难得出以上这些省市之所以在第一主因子中排到较为靠前的位置，一方面是由于其经济实力本身较强，但另一方面也和其地域大小有关。比如，上海在这项因子中并未排得十分靠前，北京甚至不在此列，其原因在很大程度上是由于尽管北京、上海发展速度惊人，但其毕竟只是城市，从地域广阔程度上讲要大大小于其他某些省份，因此在总量上也要处于劣势。

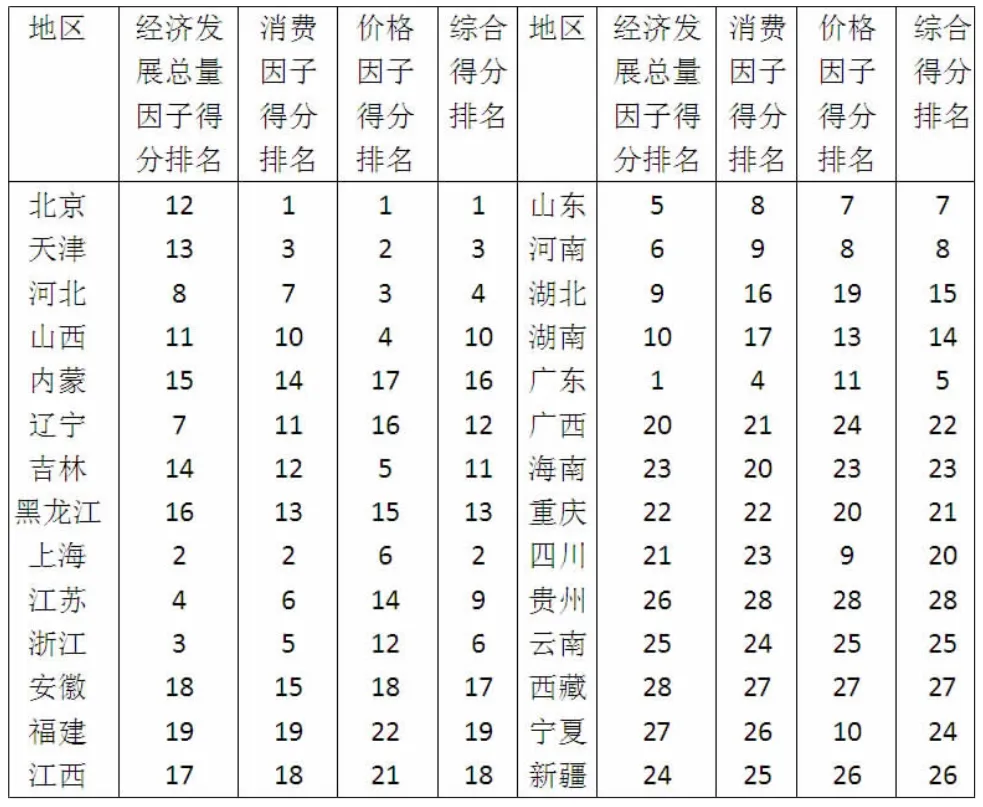
表4：各省、市、自治区的因子得分排名

第二主因子（即消费因子）能更为客观地反映经济发展，其中得分较高的省市有：北京、上海、天津、浙江、广东、江苏。职工平均工资和居民消费水平从侧面反映了人民生活水平的高低，但是其必须与物价水平高低相联系，否则也不能解释经济运行的真实状况。由于此项因子去除了地域大小的影响，具体到每个居民身上，因此较为公平，也能提供更为清晰的认识。

第三主因子（即价格因子）得分较高的省市主要有：北京、天津、河北、山西、吉林、山东、河南、上海、四川、宁夏。这项因子可以在一定程度上反映各个省市的物价情况，在价格因子的得分上排名较为靠前的省市基本上在综合因子得分上排名也较为靠前，但同样可以看到在近年来的经济发展较有起色的地区，如宁夏，它们的经济发展综合得分并不十分靠前，均居全国平均水平之下，但是物价指数都比较高，在一定程度上也说明这些地区的居民生活水平有待提高。

[1]汪冬华.多元统计分析与SPSS应用（第二版）[M].华东理工大学出版社，2011，（6）.

[2]Wolfgang Hardle，Leopold Simar.应用多元统计分析（第二版）[M]，北京大学出版社，2011，（1）.

[3]陈胜可.SPSS统计分析[M],清华大学出版社，2010，（8）.

[4]冯燕，张梅青.我国各省（市、自治区）区域竞争力的多元统计分析[J].2007，（6）.

[5]何雄浪.我国地区经济差异的实证分析[J].2004，（11）.